Las pruebas de la relatividad general sirven para establecer evidencias observacionales de la teoría de la relatividad general . Las tres primeras pruebas, propuestas por Albert Einstein en 1915, se referían a la precesión "anómala" del perihelio de Mercurio , la curvatura de la luz en campos gravitatorios y el corrimiento al rojo gravitacional . La precesión de Mercurio ya era conocida; en 1919 se realizaron experimentos que mostraban la curvatura de la luz de acuerdo con las predicciones de la relatividad general , y en pruebas posteriores se realizaron mediciones cada vez más precisas; y los científicos afirmaron haber medido el corrimiento al rojo gravitacional en 1925, aunque no se realizaron mediciones lo suficientemente sensibles como para confirmar realmente la teoría hasta 1954. Un programa más preciso que comenzó en 1959 probó la relatividad general en el límite del campo gravitacional débil, limitando severamente las posibles desviaciones de la teoría.
En la década de 1970, los científicos comenzaron a realizar pruebas adicionales, comenzando con la medición de Irwin Shapiro del retraso temporal relativista en el tiempo de viaje de la señal de radar cerca del Sol. A partir de 1974, Hulse , Taylor y otros estudiaron el comportamiento de los púlsares binarios que experimentan campos gravitatorios mucho más fuertes que los encontrados en el Sistema Solar. Tanto en el límite de campo débil (como en el Sistema Solar) como con los campos más fuertes presentes en los sistemas de púlsares binarios, las predicciones de la relatividad general han sido extremadamente bien probadas.
En febrero de 2016, el equipo LIGO Avanzado anunció que había detectado directamente ondas gravitacionales provenientes de una fusión de agujeros negros. [1] Este descubrimiento, junto con otras detecciones anunciadas en junio de 2016 y junio de 2017, [2] puso a prueba la relatividad general en el límite de campo muy fuerte, sin observar hasta la fecha desviaciones de la teoría.
Albert Einstein propuso [3] [4] tres pruebas de la relatividad general, posteriormente llamadas "pruebas clásicas" de la relatividad general, en 1916:
En la carta a The Times (de Londres) del 28 de noviembre de 1919, describió la teoría de la relatividad y agradeció a sus colegas ingleses por su comprensión y comprobación de su trabajo. También mencionó tres pruebas clásicas con comentarios: [5]

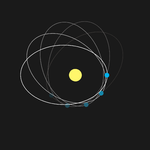
Según la física newtoniana , un objeto en un sistema (aislado) de dos cuerpos, que consiste en el objeto orbitando una masa esférica, trazaría una elipse con el centro de masa del sistema en un foco de la elipse. El punto de aproximación más cercano, llamado periapsis (o cuando el cuerpo central es el Sol, perihelio ), es fijo. Por lo tanto, el eje mayor de la elipse permanece fijo en el espacio. Ambos objetos orbitan alrededor del centro de masa de este sistema, por lo que cada uno tiene su propia elipse. Sin embargo, una serie de efectos en el Sistema Solar hacen que los perihelios de los planetas precesen (roten) alrededor del Sol en el plano de sus órbitas o, equivalentemente, hacen que el eje mayor rote sobre el centro de masa, cambiando así su orientación en el espacio. [6] La causa principal es la presencia de otros planetas que perturban la órbita de los demás. Otro efecto (mucho menos significativo) es la achatación solar .
Mercurio se desvía de la precesión predicha a partir de estos efectos newtonianos. Esta tasa anómala de precesión del perihelio de la órbita de Mercurio fue reconocida por primera vez en 1859 como un problema en la mecánica celeste , por Urbain Le Verrier . Su nuevo análisis de las observaciones cronometradas disponibles de los tránsitos de Mercurio sobre el disco solar desde 1697 hasta 1848 mostró que la tasa real de precesión discrepaba de la predicha a partir de la teoría de Newton en 38″ ( segundos de arco ) por siglo tropical (posteriormente reestimada en 43″ por Simon Newcomb en 1882). [7] Se propusieron varias soluciones ad hoc y finalmente infructuosas, pero tendían a introducir más problemas. Le Verrier sugirió que podría existir otro planeta hipotético para explicar el comportamiento de Mercurio. [7] La búsqueda exitosa previa de Neptuno basada en sus perturbaciones de la órbita de Urano llevó a los astrónomos a dar cierta fe en esta posible explicación, y el planeta hipotético incluso fue llamado Vulcano . Finalmente, en 1908, WW Campbell , Director del Observatorio Lick, después de las exhaustivas observaciones fotográficas del astrónomo de Lick, Charles D. Perrine , en tres expediciones de eclipses solares, declaró: "En mi opinión, el trabajo del Dr. Perrine en los tres eclipses de 1901, 1905 y 1908 cierra definitivamente el lado observacional del famoso problema de los planetas intramercuriales". [8] [9] Posteriormente, no se encontró evidencia de Vulcano y la teoría general de Einstein de 1915 explicó la precesión anómala de Mercurio. Einstein escribió a Michael Besso: "Los movimientos del perihelio explicados cuantitativamente... te sorprenderán". [10]
En la relatividad general, esta precesión restante , o cambio de orientación de la elipse orbital dentro de su plano orbital, se explica por la influencia de la gravitación en la curvatura del espacio-tiempo. Einstein demostró que la relatividad general [3] coincide estrechamente con la cantidad observada de desplazamiento del perihelio. Este fue un factor poderoso que motivó la adopción de la relatividad general.
Aunque las mediciones anteriores de las órbitas planetarias se hacían con telescopios convencionales, ahora se hacen mediciones más precisas con radar . La precesión total observada de Mercurio es (574,10 ± 0,65)″ por siglo [11] en relación con el ICRF inercial . Esta precesión se puede atribuir a las siguientes causas:
La corrección por (42,980 ± 0,001)″/cy es la predicción de la teoría post-newtoniana con parámetros . [13] Por lo tanto, el efecto puede explicarse completamente mediante la relatividad general. Los cálculos más recientes basados en mediciones más precisas no han cambiado materialmente la situación.
En relatividad general, el desplazamiento del perihelio σ , expresado en radianes por revolución, viene dado aproximadamente por: [14]
donde L es el semieje mayor , T es el período orbital , c es la velocidad de la luz y e es la excentricidad orbital (ver: Problema de dos cuerpos en relatividad general ).
Los demás planetas también experimentan desplazamientos del perihelio, pero, como están más alejados del Sol y tienen períodos más largos, sus desplazamientos son menores y no pudieron observarse con precisión hasta mucho después del de Mercurio. Por ejemplo, el desplazamiento del perihelio de la órbita de la Tierra debido a la relatividad general es teóricamente de 3,83868″ por siglo y experimentalmente de (3,8387 ± 0,0004)″/cy, el de Venus es de 8,62473″/cy y (8,6247 ± 0,0005)″/cy y el de Marte es de (1,351 ± 0,001)″/cy. Ambos valores ya se han medido, con resultados que concuerdan bien con la teoría. [15] El desplazamiento del periapsis también se ha medido ahora para sistemas binarios de púlsares, con PSR 1913+16 que asciende a 4,2° por año. [16] Estas observaciones son consistentes con la relatividad general. [17] También es posible medir el desplazamiento del periapsis en sistemas binarios de estrellas que no contienen estrellas ultradensas, pero es más difícil modelar los efectos clásicos con precisión; por ejemplo, es necesario conocer la alineación del giro de las estrellas con su plano orbital y es difícil de medir directamente. Se han medido algunos sistemas, como DI Herculis , [18] como casos de prueba para la relatividad general.

Henry Cavendish en 1784 (en un manuscrito inédito) y Johann Georg von Soldner en 1801 (publicado en 1804) habían señalado que la gravedad newtoniana predice que la luz de las estrellas se curvará alrededor de un objeto masivo. [19] [20] El mismo valor que el de Soldner fue calculado por Einstein en 1911 basándose únicamente en el principio de equivalencia. Sin embargo, Einstein observó en 1915, en el proceso de completar la relatividad general, que su resultado de 1911 (y, por lo tanto, el resultado de Soldner de 1801) es solo la mitad del valor correcto. Einstein se convirtió en el primero en calcular el valor correcto para la curvatura de la luz: 1,75 segundos de arco para la luz que roza el Sol. [21] [22]
La primera observación de la desviación de la luz se realizó observando el cambio de posición de las estrellas a medida que pasaban cerca del Sol en la esfera celeste . Las observaciones fueron realizadas por Arthur Eddington y sus colaboradores (véase el experimento de Eddington ) durante el eclipse solar total del 29 de mayo de 1919 , [23] cuando se pudieron observar las estrellas cercanas al Sol (en ese momento en la constelación de Tauro ). [23] Las observaciones se realizaron simultáneamente en las ciudades de Sobral, Ceará , Brasil y en Santo Tomé y Príncipe en la costa occidental de África. [24] El resultado se consideró una noticia espectacular y apareció en la portada de la mayoría de los periódicos importantes. Hizo que Einstein y su teoría de la relatividad general fueran mundialmente famosos. Cuando su asistente le preguntó cuál habría sido su reacción si la relatividad general no hubiera sido confirmada por Eddington y Dyson en 1919, Einstein hizo la famosa broma: "Entonces sentiría pena por el querido Señor. La teoría es correcta de todos modos". [25]
Sin embargo, la precisión inicial fue pobre y había dudas de que el pequeño número de ubicaciones de estrellas medidas y preguntas sobre el instrumento pudieran producir un resultado confiable. Algunos [26] argumentaron que los resultados estuvieron plagados de error sistemático y posiblemente sesgo de confirmación , aunque el reanálisis moderno del conjunto de datos [27] sugiere que el análisis de Eddington fue preciso. [28] [29] La medición fue repetida por un equipo del Observatorio Lick dirigido por el Director WW Campbell en el eclipse de 1922 observado en la remota estación australiana de Wallal , [30] con resultados basados en cientos de posiciones de estrellas que coincidían con los resultados de 1919 [29] y se ha repetido varias veces desde entonces, más notablemente en 1953 por astrónomos del Observatorio Yerkes [31] y en 1973 por un equipo de la Universidad de Texas . [32] Una considerable incertidumbre permaneció en estas mediciones durante casi cincuenta años, hasta que comenzaron a realizarse observaciones en frecuencias de radio . [33] [34] También se ha medido la desviación de la luz estelar por la cercana estrella enana blanca Stein 2051 B. [35]

Einstein predijo el corrimiento al rojo gravitacional de la luz a partir del principio de equivalencia en 1907, y se predijo que este efecto podría medirse en las líneas espectrales de una estrella enana blanca , que tiene un campo gravitacional muy alto. Los intentos iniciales de medir el corrimiento al rojo gravitacional del espectro de Sirio-B fueron realizados por Walter Sydney Adams en 1925, pero el resultado fue criticado por ser inutilizable debido a la contaminación de la luz de la estrella primaria (mucho más brillante), Sirio . [36] [37] La primera medición precisa del corrimiento al rojo gravitacional de una enana blanca fue realizada por Popper en 1954, midiendo un corrimiento al rojo gravitacional de 21 km/s de 40 Eridani B. [37]
El corrimiento al rojo de Sirio B fue finalmente medido por Greenstein et al. en 1971, obteniendo el valor del corrimiento al rojo gravitacional de89 ± 16 km/s , con mediciones más precisas del telescopio espacial Hubble que muestran80,4 ± 4,8 km/s . [38]
La teoría general de la relatividad incorpora la teoría especial de la relatividad de Einstein y, por lo tanto, las pruebas de la relatividad especial también están probando aspectos de la relatividad general. Como consecuencia del principio de equivalencia , la invariancia de Lorentz se cumple localmente en sistemas de referencia no rotatorios y en caída libre. Los experimentos relacionados con la invariancia de Lorentz de la relatividad especial (es decir, cuando los efectos gravitacionales pueden ignorarse) se describen en las pruebas de la relatividad especial .
La era moderna de las pruebas de la relatividad general se inició en gran medida gracias al impulso de Dicke y Schiff , quienes establecieron un marco para probar la relatividad general. [39] [40] [41] Ellos enfatizaron la importancia no solo de las pruebas clásicas, sino también de los experimentos nulos, que prueban efectos que en principio podrían ocurrir en una teoría de la gravitación, pero que no ocurren en la relatividad general. Otros desarrollos teóricos importantes incluyeron el inicio de teorías alternativas a la relatividad general , en particular, teorías escalar-tensoriales como la teoría de Brans-Dicke ; [42] el formalismo post-newtoniano parametrizado en el que se pueden cuantificar las desviaciones de la relatividad general; y el marco del principio de equivalencia .
Experimentalmente, los nuevos avances en la exploración espacial , la electrónica y la física de la materia condensada han hecho posible realizar experimentos más precisos, como el experimento Pound-Rebka, la interferometría láser y la telémetro lunar .
Las primeras pruebas de la relatividad general se vieron obstaculizadas por la falta de competidores viables para la teoría: no estaba claro qué tipo de pruebas la distinguirían de sus competidores. La relatividad general era la única teoría relativista de la gravedad conocida compatible con la relatividad especial y las observaciones. Además, es una teoría extremadamente simple y elegante. [ ¿según quién? ] Esto cambió con la introducción de la teoría de Brans-Dicke en 1960. Esta teoría es posiblemente más simple, ya que no contiene constantes adimensionales , y es compatible con una versión del principio de Mach y la hipótesis de los grandes números de Dirac , dos ideas filosóficas que han sido influyentes en la historia de la relatividad. En última instancia, esto condujo al desarrollo del formalismo post-newtoniano parametrizado por Nordtvedt y Will , que parametriza, en términos de diez parámetros ajustables, todas las posibles desviaciones de la ley de gravitación universal de Newton hasta el primer orden en la velocidad de los objetos en movimiento ( es decir , hasta el primer orden en , donde v es la velocidad de un objeto y c es la velocidad de la luz). Esta aproximación permite analizar sistemáticamente las posibles desviaciones de la relatividad general para objetos que se mueven lentamente en campos gravitatorios débiles. Se ha hecho un gran esfuerzo para limitar los parámetros post-newtonianos y, en la actualidad, las desviaciones de la relatividad general están muy limitadas.
Los experimentos que ponen a prueba el efecto de lente gravitacional y el retardo temporal de la luz limitan el mismo parámetro post-newtoniano, el llamado parámetro de Eddington γ, que es una parametrización sencilla de la cantidad de desviación de la luz por una fuente gravitacional. Es igual a uno para la relatividad general y toma valores diferentes en otras teorías (como la teoría de Brans-Dicke). Es el mejor restringido de los diez parámetros post-newtonianos, pero hay otros experimentos diseñados para restringir los demás. Las observaciones precisas del desplazamiento del perihelio de Mercurio restringen otros parámetros, al igual que las pruebas del principio de equivalencia fuerte.
Uno de los objetivos de la misión BepiColombo a Mercurio es probar la teoría de la relatividad general midiendo los parámetros gamma y beta del formalismo post-newtoniano parametrizado con alta precisión. [43] [44] El experimento es parte del Experimento de Radiociencia del Orbitador de Mercurio (MORE). [45] [46] La nave espacial fue lanzada en octubre de 2018 y se espera que entre en órbita alrededor de Mercurio en diciembre de 2025.
Una de las pruebas más importantes es la de lente gravitacional . Se ha observado en fuentes astrofísicas distantes, pero estas están mal controladas y no se sabe con certeza cómo restringen la relatividad general. Las pruebas más precisas son análogas al experimento de Eddington de 1919: miden la desviación de la radiación de una fuente distante por el Sol. Las fuentes que se pueden analizar con mayor precisión son las fuentes de radio distantes . En particular, algunos cuásares son fuentes de radio muy fuertes. La resolución direccional de cualquier telescopio está limitada en principio por la difracción; para los radiotelescopios, este es también el límite práctico. Una mejora importante en la obtención de altas precisiones posicionales (desde milisegundos de arco hasta microsegundos de arco) se obtuvo combinando radiotelescopios a lo largo de la Tierra. La técnica se llama interferometría de línea de base muy larga (VLBI). Con esta técnica, las observaciones de radio acoplan la información de fase de la señal de radio observada en telescopios separados a grandes distancias. Recientemente, estos telescopios han medido la desviación de las ondas de radio por el Sol con una precisión extremadamente alta, confirmando la cantidad de desviación predicha por el aspecto de la relatividad general al nivel de 0,03%. [47] En este nivel de precisión, los efectos sistemáticos deben tenerse cuidadosamente en cuenta para determinar la ubicación precisa de los telescopios en la Tierra. Algunos efectos importantes son la nutación de la Tierra , la rotación, la refracción atmosférica, el desplazamiento tectónico y los maremotos. Otro efecto importante es la refracción de las ondas de radio por la corona solar . Afortunadamente, este efecto tiene un espectro característico , mientras que la distorsión gravitacional es independiente de la longitud de onda. Por lo tanto, un análisis cuidadoso, utilizando mediciones en varias frecuencias, puede restar esta fuente de error.
Todo el cielo está ligeramente distorsionado debido a la desviación gravitacional de la luz causada por el Sol (exceptuando la dirección opuesta al Sol). Este efecto ha sido observado por el satélite astrométrico Hipparcos de la Agencia Espacial Europea . Midió las posiciones de aproximadamente 10 5 estrellas. Durante la misión completa, aproximadamenteSe han determinado 3,5 × 10 6 posiciones relativas, cada una con una precisión de 3 milisegundos de arco (la precisión para una estrella de magnitud 8-9). Dado que la desviación gravitacional perpendicular a la dirección Tierra-Sol es ya de 4,07 milisegundos de arco, se necesitan correcciones para prácticamente todas las estrellas. Sin efectos sistemáticos, el error en una observación individual de 3 milisegundos de arco podría reducirse por la raíz cuadrada del número de posiciones, lo que lleva a una precisión de 0,0016 milisegundos de arco. Sin embargo, los efectos sistemáticos limitan la precisión de la determinación al 0,3% (Froeschlé, 1997).
La sonda espacial Gaia , lanzada en 2013, realizará un censo de mil millones de estrellas de la Vía Láctea y medirá sus posiciones con una precisión de 24 microsegundos de arco. Por tanto, también proporcionará nuevas pruebas rigurosas de la desviación gravitacional de la luz causada por el Sol , que fue predicha por la relatividad general. [48]
Irwin I. Shapiro propuso otra prueba, más allá de las pruebas clásicas, que podría realizarse dentro del Sistema Solar. A veces se la llama la cuarta prueba "clásica" de la relatividad general . Predijo un retraso temporal relativista ( retardo de Shapiro ) en el tiempo de viaje de ida y vuelta para las señales de radar que se reflejan en otros planetas. [49] La mera curvatura de la trayectoria de un fotón que pasa cerca del Sol es demasiado pequeña para tener un efecto de retraso observable (cuando se compara el tiempo de ida y vuelta con el tiempo que tardaría si el fotón hubiera seguido una trayectoria recta), pero la relatividad general predice un retraso temporal que se hace progresivamente mayor cuando el fotón pasa más cerca del Sol debido a la dilatación del tiempo en el potencial gravitatorio del Sol. Observar los reflejos de radar de Mercurio y Venus justo antes y después de que sean eclipsados por el Sol concuerda con la teoría de la relatividad general en el nivel del 5%. [50]
Más recientemente, la sonda Cassini ha llevado a cabo un experimento similar que dio un acuerdo con la relatividad general en el nivel de 0,002%. [51] Sin embargo, los siguientes estudios detallados [52] [53] revelaron que el valor medido del parámetro PPN gamma se ve afectado por el efecto gravitomagnético causado por el movimiento orbital del Sol alrededor del baricentro del sistema solar. El efecto gravitomagnético en el experimento de radiociencia Cassini fue postulado implícitamente por B. Bertotti como de origen relativista general puro, pero su valor teórico nunca se ha probado en el experimento, lo que efectivamente hace que la incertidumbre experimental en el valor medido de gamma sea en realidad mayor (por un factor de 10) que el 0,002% afirmado por B. Bertotti y coautores en Nature.
La interferometría de línea de base muy larga ha medido correcciones dependientes de la velocidad (gravitomagnéticas) al retardo de tiempo de Shapiro en el campo de Júpiter en movimiento [54] [55] y Saturno. [56]
El principio de equivalencia, en su forma más simple, afirma que las trayectorias de los cuerpos que caen en un campo gravitatorio deberían ser independientes de su masa y estructura interna, siempre que sean lo suficientemente pequeños como para no perturbar el medio ambiente o verse afectados por fuerzas de marea . Esta idea ha sido probada con una precisión extremadamente alta mediante los experimentos de equilibrio de torsión de Eötvös , que buscan una aceleración diferencial entre dos masas de prueba. Las restricciones sobre esto y sobre la existencia de una quinta fuerza dependiente de la composición o interacción gravitatoria de Yukawa son muy fuertes y se analizan en el apartado de quinta fuerza y principio de equivalencia débil .
Una versión del principio de equivalencia, llamada principio de equivalencia fuerte , afirma que los cuerpos que caen por autogravitación, como las estrellas, los planetas o los agujeros negros (que se mantienen unidos por su atracción gravitatoria) deberían seguir las mismas trayectorias en un campo gravitatorio, siempre que se cumplan las mismas condiciones. Esto se llama efecto Nordtvedt y se prueba con mayor precisión mediante el Experimento de medición de distancia por láser lunar . [57] [58] Desde 1969, ha medido continuamente la distancia desde varias estaciones de medición de distancia en la Tierra hasta reflectores en la Luna con una precisión de aproximadamente centímetros. [59] Estos han proporcionado una fuerte restricción en varios de los otros parámetros post-newtonianos.
Otra parte del principio de equivalencia fuerte es el requisito de que la constante gravitacional de Newton sea constante en el tiempo y tenga el mismo valor en todas partes del universo. Hay muchas observaciones independientes que limitan la posible variación de la constante gravitacional de Newton , [60] pero una de las mejores proviene de la medición de distancias lunares que sugiere que la constante gravitacional no cambia en más de una parte en 10 11 por año. La constancia de las otras constantes se analiza en la sección del principio de equivalencia de Einstein del artículo sobre el principio de equivalencia.
La primera de las pruebas clásicas analizadas anteriormente, el corrimiento al rojo gravitacional , es una consecuencia simple del principio de equivalencia de Einstein y fue predicha por Einstein en 1907. Como tal, no es una prueba de la relatividad general de la misma manera que las pruebas post-newtonianas, porque cualquier teoría de la gravedad que obedezca el principio de equivalencia también debería incorporar el corrimiento al rojo gravitacional. No obstante, confirmar la existencia del efecto fue una importante sustanciación de la gravedad relativista, ya que la ausencia de corrimiento al rojo gravitacional habría contradicho fuertemente la relatividad. La primera observación del corrimiento al rojo gravitacional fue la medición del desplazamiento en las líneas espectrales de la estrella enana blanca Sirio B por Adams en 1925, analizada anteriormente, y mediciones posteriores de otras enanas blancas. Sin embargo, debido a la dificultad de la medición astrofísica, fue preferible la verificación experimental utilizando una fuente terrestre conocida.
La verificación experimental del corrimiento al rojo gravitacional utilizando fuentes terrestres llevó varias décadas, porque es difícil encontrar relojes (para medir la dilatación del tiempo ) o fuentes de radiación electromagnética (para medir el corrimiento al rojo) con una frecuencia que se conozca lo suficientemente bien como para que el efecto pueda medirse con precisión. Se confirmó experimentalmente por primera vez en 1959 utilizando mediciones del cambio en la longitud de onda de los fotones de rayos gamma generados con el efecto Mössbauer , que genera radiación con un ancho de línea muy estrecho. El experimento de Pound-Rebka midió el corrimiento al rojo relativo de dos fuentes situadas en la parte superior e inferior de la torre Jefferson de la Universidad de Harvard. [61] [62] El resultado estuvo en excelente acuerdo con la relatividad general. Este fue uno de los primeros experimentos de precisión que probó la relatividad general. El experimento fue mejorado más tarde por Pound y Snider para mejorar el nivel del 1%. [63]
El corrimiento al azul de un fotón que cae se puede encontrar suponiendo que tiene una masa equivalente basada en su frecuencia E = hf (donde h es la constante de Planck ) junto con E = mc2 , un resultado de la relatividad especial. Estas derivaciones simples ignoran el hecho de que en la relatividad general el experimento compara frecuencias de reloj, en lugar de energías. En otras palabras, la "mayor energía" del fotón después de que cae se puede atribuir de manera equivalente al funcionamiento más lento de los relojes en las profundidades del pozo de potencial gravitatorio. Para validar completamente la relatividad general, es importante demostrar también que la tasa de llegada de los fotones es mayor que la tasa a la que se emiten. En 1976 se realizó un experimento de corrimiento al rojo gravitatorio muy preciso, que trata este tema, [64] donde se lanzó un reloj máser de hidrógeno en un cohete a una altura de 10.000 km, y se comparó su tasa con un reloj idéntico en tierra. Se probó el corrimiento al rojo gravitatorio al 0,007%.
Aunque el Sistema de Posicionamiento Global (GPS) no está diseñado para poner a prueba la física fundamental, debe tener en cuenta el corrimiento al rojo gravitacional en su sistema de cronometraje, y los físicos han analizado los datos de cronometraje del GPS para confirmar otras pruebas. Cuando se lanzó el primer satélite, algunos ingenieros se resistieron a la predicción de que se produciría una dilatación notable del tiempo gravitacional, por lo que el primer satélite se lanzó sin el ajuste del reloj que se incorporó posteriormente a los satélites posteriores. El resultado fue el desplazamiento previsto de 38 microsegundos por día. Esta tasa de discrepancia es suficiente para perjudicar sustancialmente el funcionamiento del GPS en cuestión de horas si no se tiene en cuenta. En Ashby 2003 se puede encontrar una excelente explicación del papel desempeñado por la relatividad general en el diseño del GPS. [65]
Otras pruebas de precisión de la relatividad general, [66] no analizadas aquí, son el satélite Gravity Probe A , lanzado en 1976, que mostró que la gravedad y la velocidad afectan la capacidad de sincronizar las frecuencias de los relojes que orbitan una masa central y el experimento Hafele-Keating , que utilizó relojes atómicos en aviones que circunnavegaban para probar la relatividad general y la relatividad especial juntas. [67] [68]

Se han realizado pruebas de la precesión Lense-Thirring , que consiste en pequeñas precesiones seculares de la órbita de una partícula de prueba en movimiento alrededor de una masa giratoria central, por ejemplo, un planeta o una estrella, con los satélites LAGEOS , [69] pero muchos aspectos de ellas siguen siendo controvertidos. El mismo efecto puede haber sido detectado en los datos de la nave espacial Mars Global Surveyor (MGS), una antigua sonda en órbita alrededor de Marte ; también una prueba de este tipo generó un debate. [70] También se han informado recientemente los primeros intentos de detectar el efecto Lense-Thirring del Sol en los perihelios de los planetas interiores . El arrastre de marco causaría que el plano orbital de las estrellas que orbitan cerca de un agujero negro supermasivo precesara alrededor del eje de giro del agujero negro. Este efecto debería ser detectable en los próximos años a través del monitoreo astrométrico de las estrellas en el centro de la galaxia de la Vía Láctea . [71] Comparando la tasa de precesión orbital de dos estrellas en órbitas diferentes, es posible en principio probar los teoremas de ausencia de pelo de la relatividad general. [72]
El satélite Gravity Probe B , lanzado en 2004 y en funcionamiento hasta 2005, detectó el arrastre de trama y el efecto geodésico . El experimento utilizó cuatro esferas de cuarzo del tamaño de pelotas de ping pong recubiertas de un superconductor. El análisis de datos continuó durante 2011 debido a los altos niveles de ruido y las dificultades para modelar el ruido con precisión de modo que se pudiera encontrar una señal útil. Los investigadores principales de la Universidad de Stanford informaron el 4 de mayo de 2011 que habían medido con precisión el efecto de arrastre de trama en relación con la estrella distante IM Pegasi , y los cálculos demostraron estar en línea con la predicción de la teoría de Einstein. Los resultados, publicados en Physical Review Letters , midieron el efecto geodésico con un error de aproximadamente el 0,2 por ciento. Los resultados informaron que el efecto de arrastre de trama (causado por la rotación de la Tierra) sumó 37 milisegundos de arco con un error de aproximadamente el 19 por ciento. [73] El investigador Francis Everitt explicó que un milisegundo de arco "es el ancho de un cabello humano visto a una distancia de 10 millas". [74]
En enero de 2012, el satélite LARES fue lanzado en un cohete Vega [75] para medir el efecto Lense-Thirring con una precisión de alrededor del 1%, según sus defensores. [76] Esta evaluación de la precisión real obtenible es un tema de debate. [77] [78] [79]
Es posible comprobar si el potencial gravitatorio continúa con la ley del cuadrado inverso a distancias muy pequeñas. Las pruebas realizadas hasta ahora se han centrado en una divergencia de la RG en forma de un potencial de Yukawa , pero no se ha encontrado ninguna evidencia de un potencial de este tipo. El potencial de Yukawa con ha sido descartado hasta λ =5,6 × 10 −5 m . [80]
Fue concebido como un medio para medir el efecto de dilatación del tiempo en la Tierra después de estar motivado por el principio de equivalencia de Einstein que implica que un observador giratorio estará sujeto a las mismas transformaciones que un observador en un campo gravitacional. [81] Los experimentos con rotor de Mössbauer permiten, por tanto, una prueba terrestre precisa del efecto Doppler relativista . Desde una fuente radiactiva fijada en el centro de un disco o varilla giratoria, los rayos gamma viajan a un absorbedor en el borde (en algunas variaciones del experimento, este esquema se invirtió) y un número no absorbido de ellos pasa dependiendo de la velocidad de rotación para llegar a un contador estacionario ( es decir , detector de cuantos gamma en reposo en el marco del laboratorio). En lugar de la hipótesis del reloj , la relatividad general de Einstein predice que el reloj del absorbedor en movimiento en el borde debería retrasarse una cantidad específica debido a la dilatación del tiempo debido solo al enlace centrífugo en comparación con un absorbedor en el marco de reposo. Por lo tanto, la transmisión de fotones gamma a través del absorbedor debería aumentar durante la rotación, lo que puede medirse posteriormente mediante el contador estacionario más allá del absorbedor. Esta predicción se observó realmente utilizando el efecto Mössbauer , ya que el principio de equivalencia, como lo sugirió originalmente Einstein, permite implícitamente la asociación de la dilatación del tiempo debido a la rotación (calculada como resultado del cambio en la tasa de conteo del detector) con la dilatación del tiempo gravitacional. Tales experimentos fueron pioneros por Hay et al. (1960), [82] Champeney et al. (1965), [83] y Kündig (1963), [84] y todos ellos habían declarado la confirmación de la predicción de la teoría de la relatividad de Einstein.
Sea como fuere, un reexamen de estos esfuerzos a principios del siglo XXI puso en tela de juicio la validez de los resultados obtenidos en el pasado que afirmaban haber verificado la dilatación del tiempo según lo predicho por la teoría de la relatividad de Einstein, [85] [86] mediante los cuales se llevaron a cabo nuevos experimentos que descubrieron un cambio de energía adicional entre la radiación emitida y absorbida junto a la dilatación relativista clásica del tiempo. [87] [88] Este descubrimiento se explicó primero como un descrédito de la relatividad general y una confirmación exitosa a escala de laboratorio de las predicciones de una teoría alternativa de la gravedad desarrollada por T. Yarman y sus colegas. [89] En contra de este desarrollo, se hizo un intento polémico de explicar el cambio de energía adicional revelado como el resultado de un efecto de sincronización del reloj hasta ahora desconocido y supuestamente perdido , [90] [91] que inusualmente fue galardonado con un premio en 2018 por la Gravity Research Foundation por haber asegurado una nueva prueba de la relatividad general . [92] Sin embargo, en el mismo período de tiempo, se reveló que dicho autor cometió varios errores matemáticos en sus cálculos, [93] y la supuesta contribución de la llamada sincronización del reloj a la dilatación del tiempo medida es de hecho prácticamente nula. [94] [95] [96] [97] [98] [99] Como consecuencia, una explicación relativista general para los resultados de los experimentos del rotor Mössbauer permanece abierta.
Los campos gravitatorios muy fuertes que están presentes cerca de los agujeros negros , especialmente aquellos agujeros negros supermasivos que se cree que alimentan los núcleos galácticos activos y los cuásares más activos , pertenecen a un campo de investigación intensa y activa. Las observaciones de estos cuásares y núcleos galácticos activos son difíciles, y la interpretación de las observaciones depende en gran medida de modelos astrofísicos distintos de la relatividad general o teorías fundamentales de la gravitación que compiten entre sí , pero son cualitativamente consistentes con el concepto de agujero negro tal como se modela en la relatividad general.
Los púlsares son estrellas de neutrones que giran rápidamente y emiten pulsos de radio regulares a medida que giran. Como tales, actúan como relojes que permiten un seguimiento muy preciso de sus movimientos orbitales. Las observaciones de púlsares en órbita alrededor de otras estrellas han demostrado precesiones de periapsis sustanciales que no se pueden explicar de forma clásica, pero sí mediante el uso de la relatividad general. Por ejemplo, el púlsar binario Hulse-Taylor PSR B1913+16 (un par de estrellas de neutrones en las que una se detecta como púlsar) tiene una precesión observada de más de 4° de arco por año (el desplazamiento del periastrón por órbita es de solo unos 10 −6 ). Esta precesión se ha utilizado para calcular las masas de los componentes.
De manera similar a la forma en que los átomos y las moléculas emiten radiación electromagnética, una masa gravitacional que esté en vibración de tipo cuadrupolar o de orden superior, o que sea asimétrica y esté en rotación, puede emitir ondas gravitacionales. [100] Se predice que estas ondas gravitacionales viajan a la velocidad de la luz . Por ejemplo, los planetas que orbitan alrededor del Sol pierden constantemente energía a través de la radiación gravitacional, pero este efecto es tan pequeño que es poco probable que se observe en el futuro cercano (la Tierra irradia alrededor de 200 vatios de radiación gravitacional ).
La radiación de ondas gravitacionales se ha deducido del sistema binario Hulse-Taylor (y otros púlsares binarios). [101] La cronología precisa de los pulsos muestra que las estrellas orbitan sólo aproximadamente de acuerdo con las Leyes de Kepler : con el tiempo se van acercando gradualmente en espiral, lo que demuestra una pérdida de energía en estrecha concordancia con la energía predicha radiada por las ondas gravitacionales. [102] [103] Por su descubrimiento del primer púlsar binario y la medición de su decaimiento orbital debido a la emisión de ondas gravitacionales, Hulse y Taylor ganaron el Premio Nobel de Física en 1993. [104]
Un "doble púlsar" descubierto en 2003, PSR J0737-3039 , tiene una precesión del periastrón de 16,90° por año; a diferencia del sistema binario Hulse-Taylor, ambas estrellas de neutrones se detectan como púlsares, lo que permite cronometrar con precisión ambos miembros del sistema. Debido a esto, la órbita estrecha, el hecho de que el sistema está casi de canto y la velocidad transversal muy baja del sistema visto desde la Tierra, J0737−3039 proporciona, con mucho, el mejor sistema para pruebas de campo intenso de la relatividad general conocido hasta ahora. Se observan varios efectos relativistas distintos, incluida la desintegración orbital como en el sistema Hulse-Taylor. Después de observar el sistema durante dos años y medio, fueron posibles cuatro pruebas independientes de relatividad general, la más precisa (el retardo de Shapiro) confirmó la predicción de la relatividad general dentro del 0,05% [105] (sin embargo, el desplazamiento del periastrón por órbita es solo de alrededor del 0,0013% de un círculo y, por lo tanto, no es una prueba de relatividad de orden superior).
En 2013, un equipo internacional de astrónomos informó nuevos datos de la observación de un sistema púlsar-enana blanca PSR J0348+0432 , en el que pudieron medir un cambio en el período orbital de 8 millonésimas de segundo por año, y confirmaron las predicciones de RG en un régimen de campos gravitacionales extremos nunca antes investigados; [106] pero todavía hay algunas teorías en competencia que estarían de acuerdo con estos datos. [107]
Se han construido varios detectores de ondas gravitacionales con la intención de detectar directamente las ondas gravitacionales que emanan de eventos astronómicos como la fusión de dos estrellas de neutrones o agujeros negros . En febrero de 2016, el equipo LIGO avanzado anunció que había detectado directamente ondas gravitacionales de una fusión de dos sistemas estelares binarios con agujeros negros , [1] [108] [109] y se anunciaron detecciones adicionales en junio de 2016, junio de 2017 y agosto de 2017. [2] [110]
La relatividad general predice las ondas gravitacionales, como lo hace cualquier teoría de la gravitación en la que los cambios en el campo gravitacional se propagan a una velocidad finita. [111] Entonces, la función de respuesta LIGO podría discriminar entre las diversas teorías. [112] [113] Dado que las ondas gravitacionales se pueden detectar directamente, [1] [109] es posible usarlas para aprender sobre el Universo. Esta es la astronomía de ondas gravitacionales . La astronomía de ondas gravitacionales puede probar la relatividad general verificando que las ondas observadas son de la forma predicha (por ejemplo, que solo tienen dos polarizaciones transversales), y comprobando que los agujeros negros son los objetos descritos por las soluciones de las ecuaciones de campo de Einstein . [114] [115] [116]
La astronomía de ondas gravitacionales también puede poner a prueba las ecuaciones de campo de Maxwell-Einstein. Esta versión de las ecuaciones de campo predice que los magnetares giratorios (es decir, estrellas de neutrones con un campo dipolar magnético extremadamente fuerte) deberían emitir ondas gravitacionales. [117]
«Estas sorprendentes observaciones son la confirmación de muchos trabajos teóricos, incluida la teoría general de la relatividad de Einstein, que predice las ondas gravitacionales», afirmó Stephen Hawking. [1]

La galaxia M87 fue objeto de observación por el Event Horizon Telescope (EHT) en 2017; el número del 10 de abril de 2019 de Astrophysical Journal Letters (vol. 875, No. 1) estuvo dedicado a los resultados del EHT, publicando seis artículos de acceso abierto . El horizonte de sucesos del agujero negro en el centro de M87 fue fotografiado directamente en la longitud de onda de las ondas de radio por el EHT; la imagen fue revelada en una conferencia de prensa el 10 de abril de 2019, la primera imagen del horizonte de sucesos de un agujero negro. [119] [118] En mayo de 2022, el EHT proporcionó la primera imagen del agujero negro supermasivo Sagitario A* en el centro de nuestra propia galaxia, la Vía Láctea.
El corrimiento al rojo gravitacional de la luz de la estrella S2 que orbita el agujero negro supermasivo Sagitario A* en el centro de la Vía Láctea se ha medido con el Very Large Telescope utilizando los instrumentos GRAVITY, NACO y SIFONI. [120] [121] Además, ahora se ha detectado la precesión de Schwarzschild en la órbita de la estrella S2 cerca del agujero negro masivo del centro galáctico. [122]
El principio de equivalencia fuerte de la relatividad general requiere la universalidad de la caída libre para aplicarse incluso a cuerpos con fuerte autogravedad. Las pruebas directas de este principio utilizando cuerpos del Sistema Solar están limitadas por la débil autogravedad de los cuerpos, y las pruebas utilizando sistemas binarios púlsar-enana blanca han estado limitadas por la débil atracción gravitatoria de la Vía Láctea. Con el descubrimiento de un sistema estelar triple llamado PSR J0337+1715 , ubicado a unos 4.200 años luz de la Tierra, el principio de equivalencia fuerte puede probarse con una alta precisión. Este sistema contiene una estrella de neutrones en una órbita de 1,6 días con una estrella enana blanca , y el par en una órbita de 327 días con otra enana blanca más alejada. Este sistema permite una prueba que compara cómo la atracción gravitatoria de la enana blanca exterior afecta al púlsar, que tiene fuerte autogravedad, y a la enana blanca interior. El resultado muestra que las aceleraciones del púlsar y su compañera enana blanca cercana difieren fraccionariamente en no más de 2,6 × 10 −6 ( nivel de confianza del 95% ). [123] [124] [125]
Esta técnica se basa en la idea de que las trayectorias de los fotones se modifican en presencia de un cuerpo gravitacional. Un sistema astrofísico muy común en el universo es un agujero negro rodeado por un disco de acreción . La radiación del entorno general, incluido el disco de acreción, se ve afectada por la naturaleza del agujero negro central. Suponiendo que la teoría de Einstein sea correcta, los agujeros negros astrofísicos se describen mediante la métrica de Kerr. (Una consecuencia de los teoremas de ausencia de pelo ). Por lo tanto, al analizar la radiación de tales sistemas, es posible probar la teoría de Einstein.
La mayor parte de la radiación de estos sistemas de disco de acreción de agujeros negros (por ejemplo, sistemas binarios de agujeros negros y núcleos galácticos activos ) llega en forma de rayos X. Cuando se modela, la radiación se descompone en varios componentes. Las pruebas de la teoría de Einstein son posibles con el espectro térmico (solo para sistemas binarios de agujeros negros) y el espectro de reflexión (tanto para sistemas binarios de agujeros negros como para núcleos galácticos activos). No se espera que el primero proporcione fuertes restricciones, [126] mientras que el segundo es mucho más prometedor. [127] En ambos casos, las incertidumbres sistemáticas podrían hacer que tales pruebas sean más desafiantes. [128]
Las pruebas de la relatividad general en las escalas más grandes no son tan estrictas como las pruebas del Sistema Solar. [129] La primera prueba de este tipo fue la predicción y el descubrimiento de la expansión del universo . [130] En 1922, Alexander Friedmann descubrió que las ecuaciones de Einstein tienen soluciones no estacionarias (incluso en presencia de la constante cosmológica ). [131] [132] En 1927, Georges Lemaître demostró que las soluciones estáticas de las ecuaciones de Einstein, que son posibles en presencia de la constante cosmológica, son inestables y, por lo tanto, el universo estático imaginado por Einstein no podría existir (debe expandirse o contraerse). [131] Lemaître hizo una predicción explícita de que el universo debería expandirse. [133] También derivó una relación desplazamiento al rojo-distancia, que ahora se conoce como la Ley de Hubble . [133] Más tarde, en 1931, el propio Einstein estuvo de acuerdo con los resultados de Friedmann y Lemaître. [131] La expansión del universo descubierta por Edwin Hubble en 1929 [131] fue considerada por muchos (y continúa siendo considerada por algunos ahora) como una confirmación directa de la relatividad general. [134] En la década de 1930, en gran parte debido al trabajo de EA Milne , se comprendió que la relación lineal entre el corrimiento al rojo y la distancia deriva del supuesto general de uniformidad e isotropía en lugar de específicamente de la relatividad general. [130] Sin embargo, la predicción de un universo no estático no era trivial, de hecho dramática, y estaba motivada principalmente por la relatividad general. [135]
Otras pruebas cosmológicas incluyen la búsqueda de ondas gravitacionales primordiales generadas durante la inflación cósmica , que pueden detectarse en la polarización del fondo cósmico de microondas [136] o mediante un interferómetro de ondas gravitacionales basado en el espacio llamado Big Bang Observer . Otras pruebas a alto corrimiento al rojo son las restricciones a otras teorías de la gravedad [137] [138] y la variación de la constante gravitacional desde la nucleosíntesis del Big Bang (no varió más del 40% desde entonces). [ cita requerida ]
En agosto de 2017 se dieron a conocer los resultados de las pruebas realizadas por astrónomos utilizando el Very Large Telescope (VLT) del Observatorio Europeo Austral , entre otros instrumentos, y demostraron positivamente los efectos gravitacionales predichos por Albert Einstein. Una de estas pruebas observó la órbita de las estrellas que giran alrededor de Sagitario A* , un agujero negro aproximadamente 4 millones de veces más masivo que el Sol. La teoría de Einstein sugería que los objetos grandes curvan el espacio a su alrededor, haciendo que otros objetos diverjan de las líneas rectas que de otro modo seguirían. Aunque estudios anteriores han validado la teoría de Einstein, esta fue la primera vez que su teoría se había probado en un objeto tan gigantesco. Los hallazgos fueron publicados en The Astrophysical Journal . [139] [140]
Los astrónomos han utilizado el telescopio espacial Hubble y el Very Large Telescope para realizar pruebas precisas de la relatividad general a escala galáctica. La galaxia cercana ESO 325-G004 actúa como una potente lente gravitacional, distorsionando la luz procedente de una galaxia distante situada detrás de ella y creando un anillo de Einstein alrededor de su centro. Al comparar la masa de ESO 325-G004 (a partir de mediciones de los movimientos de las estrellas en el interior de esta galaxia) con la curvatura del espacio que la rodea, los astrónomos descubrieron que la gravedad se comporta como predice la relatividad general en estas escalas de longitud astronómicas. [141] [142]
{{cite book}}: CS1 maint: multiple names: authors list (link)