La relatividad especial es una teoría física que desempeña un papel fundamental en la descripción de todos los fenómenos físicos, siempre que la gravitación no sea significativa. Muchos experimentos desempeñaron (y aún desempeñan) un papel importante en su desarrollo y justificación. La fortaleza de la teoría reside en su capacidad única para predecir correctamente y con gran precisión el resultado de una gama extremadamente diversa de experimentos. Todavía se realizan repeticiones de muchos de esos experimentos con una precisión cada vez mayor, y los experimentos modernos se centran en efectos como los de la escala de Planck y en el sector de neutrinos . Sus resultados son consistentes con las predicciones de la relatividad especial. Jakob Laub , [1] Zhang, [2] Mattingly, [3] Clifford Will , [4] y Roberts/Schleif proporcionaron recopilaciones de varias pruebas . [5]
La relatividad especial se limita al espacio-tiempo plano , es decir , a todos los fenómenos sin influencia significativa de la gravitación . Esta última se encuentra en el dominio de la relatividad general y deben considerarse las pruebas correspondientes de la relatividad general .
La teoría predominante de la luz en el siglo XIX era la del éter luminífero , un medio estacionario en el que la luz se propaga de manera análoga a la forma en que el sonido se propaga a través del aire. Por analogía, se deduce que la velocidad de la luz es constante en todas las direcciones en el éter y es independiente de la velocidad de la fuente. Por lo tanto, un observador que se mueve en relación con el éter debe medir algún tipo de "viento de éter", al igual que un observador que se mueve en relación con el aire mide un viento aparente .
A partir del trabajo de François Arago (1810), se habían llevado a cabo una serie de experimentos ópticos que deberían haber dado un resultado positivo para magnitudes de primer orden en (es decir, de ) y que, por lo tanto, deberían haber demostrado el movimiento relativo del éter. Sin embargo, los resultados fueron negativos. Augustin Fresnel (1818) proporcionó una explicación con la introducción de una hipótesis auxiliar, el llamado "coeficiente de arrastre", es decir, la materia arrastra al éter en una pequeña medida. Este coeficiente fue demostrado directamente por el experimento de Fizeau (1851). Más tarde se demostró que todos los experimentos ópticos de primer orden deben dar un resultado negativo debido a este coeficiente. Además, se llevaron a cabo algunos experimentos electrostáticos de primer orden, que nuevamente tuvieron resultados negativos. En general, Hendrik Lorentz (1892, 1895) introdujo varias variables auxiliares nuevas para observadores en movimiento, demostrando por qué todos los experimentos ópticos y electrostáticos de primer orden han producido resultados nulos. Por ejemplo, Lorentz propuso una variable de ubicación por la cual los campos electrostáticos se contraen en la línea de movimiento y otra variable ("tiempo local") por la cual las coordenadas de tiempo de los observadores en movimiento dependen de su ubicación actual. [1]

La teoría del éter estacionario, sin embargo, daría resultados positivos cuando los experimentos fueran lo suficientemente precisos para medir magnitudes de segundo orden en (es decir, de ). Albert A. Michelson realizó el primer experimento de este tipo en 1881, seguido por el experimento de Michelson-Morley más sofisticado en 1887. Se hicieron interferir dos rayos de luz, viajando durante algún tiempo en diferentes direcciones, de modo que las diferentes orientaciones relativas al viento del éter deberían conducir a un desplazamiento de las franjas de interferencia . Pero el resultado fue negativo nuevamente. La salida de este dilema fue la propuesta de George Francis FitzGerald (1889) y Lorentz (1892) de que la materia se contrae en la línea de movimiento con respecto al éter ( contracción de longitud ). Es decir, la hipótesis más antigua de una contracción de los campos electrostáticos se extendió a las fuerzas intermoleculares. Sin embargo, como no había ninguna razón teórica para eso, la hipótesis de la contracción se consideró ad hoc .
Además del experimento óptico de Michelson-Morley, también se llevó a cabo su equivalente electrodinámico, el experimento de Trouton-Noble . Con él se demostró que un condensador en movimiento debe estar sometido a un par de torsión . Además, los experimentos de Rayleigh y Brace pretendían medir algunas consecuencias de la contracción de la longitud en el marco de laboratorio, por ejemplo, la suposición de que conduciría a la birrefringencia . Aunque todos esos experimentos condujeron a resultados negativos. (El experimento de Trouton-Rankine realizado en 1908 también dio un resultado negativo al medir la influencia de la contracción de la longitud en una bobina electromagnética .) [1]
Para explicar todos los experimentos realizados antes de 1904, Lorentz se vio obligado a ampliar nuevamente su teoría introduciendo la transformación completa de Lorentz . Henri Poincaré declaró en 1905 que la imposibilidad de demostrar el movimiento absoluto ( principio de relatividad ) es aparentemente una ley de la naturaleza.
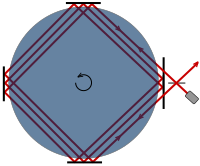
La idea de que el éter podría ser arrastrado completamente dentro o en las proximidades de la Tierra, con lo que se podrían explicar los experimentos de deriva negativa del éter, fue refutada por una variedad de experimentos.
Lodge expresó la situación paradójica en la que se encontraban los físicos de la siguiente manera: "... a ninguna velocidad practicable... la materia [tiene] ningún agarre viscoso apreciable sobre el éter. Los átomos deben ser capaces de ponerla en vibración, si están oscilando o girando a suficiente velocidad; de lo contrario, no emitirían luz ni ningún tipo de radiación; pero en ningún caso parecen arrastrarla, o encontrar resistencia en cualquier movimiento uniforme a través de ella". [6]
Finalmente, Albert Einstein (1905) llegó a la conclusión de que las teorías establecidas y los hechos conocidos en ese momento sólo forman un sistema lógico coherente cuando los conceptos de espacio y tiempo se someten a una revisión fundamental. Por ejemplo:
El resultado es la teoría de la relatividad especial , que se basa en la constancia de la velocidad de la luz en todos los sistemas de referencia inerciales y en el principio de relatividad . En este caso, la transformación de Lorentz ya no es una mera colección de hipótesis auxiliares, sino que refleja una simetría de Lorentz fundamental y constituye la base de teorías exitosas como la electrodinámica cuántica . Existe una gran cantidad de posibles pruebas de las predicciones y del segundo postulado: [7]

Los efectos de la relatividad especial pueden derivarse fenomenológicamente de los tres experimentos fundamentales siguientes: [8]
De estos tres experimentos y utilizando la sincronización de Poincaré-Einstein , se deduce la transformación completa de Lorentz, siendo el factor de Lorentz : [8]
Además de la derivación de la transformación de Lorentz, la combinación de estos experimentos también es importante porque pueden interpretarse de diferentes maneras cuando se ven individualmente. Por ejemplo, los experimentos de isotropía como Michelson-Morley pueden verse como una simple consecuencia del principio de relatividad, según el cual cualquier observador en movimiento inercial puede considerarse en reposo. Por lo tanto, por sí mismo, el experimento MM es compatible con teorías invariantes de Galileo como la teoría de la emisión o la hipótesis de arrastre completo del éter , que también contienen algún tipo de principio de relatividad. Sin embargo, cuando se consideran otros experimentos que excluyen las teorías invariantes de Galileo ( es decir , el experimento de Ives-Stilwell, varias refutaciones de las teorías de la emisión y refutaciones del arrastre completo del éter ), las teorías invariantes de Lorentz y, por lo tanto, la relatividad especial son las únicas teorías que siguen siendo viables.
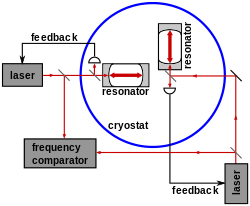
Se han llevado a cabo variantes modernas de los experimentos de Michelson-Morley y Kennedy-Thorndike para comprobar la isotropía de la velocidad de la luz. A diferencia de Michelson-Morley, los experimentos de Kennedy-Thorndike emplean longitudes de brazo diferentes y las evaluaciones duran varios meses. De esa manera, se puede observar la influencia de las diferentes velocidades durante la órbita de la Tierra alrededor del Sol. Se utilizan láseres , máseres y resonadores ópticos , lo que reduce la posibilidad de cualquier anisotropía de la velocidad de la luz al nivel de 10 −17 . Además de las pruebas terrestres, también se han llevado a cabo experimentos de medición de distancia por láser lunar como una variación del experimento de Kennedy-Thorndike. [4]
Otro tipo de experimentos de isotropía son los experimentos de rotor Mössbauer de la década de 1960, mediante los cuales se puede observar la anisotropía del efecto Doppler en un disco giratorio utilizando el efecto Mössbauer (esos experimentos también se pueden utilizar para medir la dilatación del tiempo, ver más abajo).
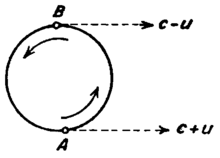
Las teorías de emisión , según las cuales la velocidad de la luz depende de la velocidad de la fuente, pueden explicar concebiblemente el resultado negativo de los experimentos de deriva del éter. No fue hasta mediados de la década de 1960 que la constancia de la velocidad de la luz se demostró definitivamente mediante experimentos, ya que en 1965, JG Fox demostró que los efectos del teorema de extinción hacían que los resultados de todos los experimentos anteriores a ese momento no fueran concluyentes y, por lo tanto, compatibles tanto con la relatividad especial como con la teoría de la emisión. [9] [10] Experimentos más recientes han descartado definitivamente el modelo de emisión: los primeros fueron los de Filippas y Fox (1964), [11] utilizando fuentes móviles de rayos gamma, y Alväger et al. (1964), [12] que demostraron que los fotones no adquirían la velocidad de los mesones de desintegración de alta velocidad que eran su fuente. Además, el experimento de la estrella doble de Sitter (1913) fue repetido por Brecher (1977) bajo consideración del teorema de extinción, descartando también una dependencia de la fuente. [13]
Las observaciones de estallidos de rayos gamma también demostraron que la velocidad de la luz es independiente de la frecuencia y la energía de los rayos de luz. [14]
Se realizaron una serie de mediciones unidireccionales, todas ellas confirmando la isotropía de la velocidad de la luz. [5] Sin embargo, solo la velocidad bidireccional de la luz (de A a B y de regreso a A) puede medirse de manera inequívoca, ya que la velocidad unidireccional depende de la definición de simultaneidad y, por lo tanto, del método de sincronización. La convención de sincronización de Einstein hace que la velocidad unidireccional sea igual a la velocidad bidireccional. Sin embargo, existen muchos modelos que tienen una velocidad de la luz bidireccional isótropa, en los que la velocidad unidireccional es anisotrópica al elegir diferentes esquemas de sincronización. Son experimentalmente equivalentes a la relatividad especial porque todos estos modelos incluyen efectos como la dilatación del tiempo de los relojes en movimiento, que compensan cualquier anisotropía medible. Sin embargo, de todos los modelos que tienen velocidad isótropa bidireccional, solo la relatividad especial es aceptable para la abrumadora mayoría de los físicos, ya que todas las demás sincronizaciones son mucho más complicadas y esos otros modelos (como la teoría del éter de Lorentz ) se basan en suposiciones extremas e inverosímiles sobre algunos efectos dinámicos, que tienen como objetivo ocultar el "marco preferido" de la observación.
Los experimentos de comparación de relojes (los procesos periódicos y las frecuencias pueden considerarse como relojes), como los experimentos de Hughes-Drever, proporcionan pruebas rigurosas de la invariancia de Lorentz . No se limitan al sector de los fotones como Michelson-Morley, sino que determinan directamente cualquier anisotropía de masa, energía o espacio midiendo el estado fundamental de los núcleos . Se ha proporcionado un límite superior de tales anisotropías de 10 −33 GeV . Por lo tanto, estos experimentos se encuentran entre las verificaciones más precisas de la invariancia de Lorentz jamás realizadas. [3] [4]

El efecto Doppler transversal y, en consecuencia, la dilatación del tiempo se observaron directamente por primera vez en el experimento de Ives-Stilwell (1938). En los experimentos modernos de Ives-Stilwell en anillos de almacenamiento de iones pesados utilizando espectroscopia saturada , la desviación máxima medida de la dilatación del tiempo con respecto a la predicción relativista se ha limitado a ≤ 10 −8 . Otras confirmaciones de la dilatación del tiempo incluyen experimentos de rotor Mössbauer en los que se enviaron rayos gamma desde el centro de un disco giratorio a un receptor en el borde del disco, de modo que el efecto Doppler transversal se puede evaluar por medio del efecto Mössbauer . Al medir la vida útil de los muones en la atmósfera y en aceleradores de partículas, también se verificó la dilatación del tiempo de las partículas en movimiento. Por otro lado, el experimento de Hafele-Keating confirmó la resolución de la paradoja de los gemelos , es decir , que un reloj que se mueve de A a B de regreso a A se retrasa con respecto al reloj inicial. Sin embargo, en este experimento los efectos de la relatividad general también juegan un papel esencial.
En la práctica, es difícil confirmar directamente la contracción de la longitud , ya que las dimensiones de las partículas observadas son extremadamente pequeñas. Sin embargo, existen confirmaciones indirectas; por ejemplo, el comportamiento de los iones pesados en colisión se puede explicar si se considera su mayor densidad debido a la contracción de Lorentz. La contracción también conduce a un aumento de la intensidad del campo de Coulomb perpendicular a la dirección del movimiento, cuyos efectos ya se han observado. Por lo tanto, tanto la dilatación del tiempo como la contracción de la longitud deben tenerse en cuenta al realizar experimentos en aceleradores de partículas.

A partir de 1901 se realizaron una serie de mediciones destinadas a demostrar la dependencia de la masa de los electrones con la velocidad . Los resultados mostraron efectivamente dicha dependencia, pero la precisión necesaria para distinguir entre teorías en pugna fue discutida durante mucho tiempo. Finalmente, fue posible descartar definitivamente todos los modelos en pugna, excepto la relatividad especial.
En la actualidad, las predicciones de la relatividad especial se confirman de forma rutinaria en aceleradores de partículas como el Relativistic Heavy Ion Collider . Por ejemplo, el aumento del momento y la energía relativistas no solo se mide con precisión, sino que también es necesario para comprender el comportamiento de los ciclotrones y sincrotrones , etc., mediante los cuales las partículas se aceleran a velocidades cercanas a la de la luz.

La relatividad especial también predice que dos rayos de luz que viajan en direcciones opuestas alrededor de una trayectoria cerrada que gira (por ejemplo, un bucle) requieren tiempos de vuelo diferentes para regresar al emisor/receptor en movimiento (esto es una consecuencia de la independencia de la velocidad de la luz con respecto a la velocidad de la fuente, véase más arriba). Este efecto fue observado y se llama efecto Sagnac . Actualmente, la consideración de este efecto es necesaria para muchas configuraciones experimentales y para el correcto funcionamiento del GPS .
Si se realizan tales experimentos en medios en movimiento (por ejemplo, agua o fibra óptica de vidrio ), también es necesario considerar el coeficiente de arrastre de Fresnel, como se demostró en el experimento de Fizeau . Aunque inicialmente se entendió que este efecto proporcionaba evidencia de un éter casi estacionario o un arrastre parcial del éter, se puede explicar fácilmente con la relatividad especial utilizando la ley de composición de la velocidad .
Se han desarrollado varias teorías de prueba para evaluar un posible resultado positivo en experimentos de violación de Lorentz añadiendo ciertos parámetros a las ecuaciones estándar. Estas incluyen el marco Robertson-Mansouri-Sexl (RMS) y la Extensión del Modelo Estándar (SME). RMS tiene tres parámetros comprobables con respecto a la contracción de la longitud y la dilatación del tiempo. A partir de eso, se puede evaluar cualquier anisotropía de la velocidad de la luz. Por otro lado, SME incluye muchos parámetros de violación de Lorentz, no solo para la relatividad especial, sino también para el modelo estándar y la relatividad general ; por lo tanto, tiene un número mucho mayor de parámetros comprobables.
Debido a los avances en los últimos años en relación con varios modelos de gravedad cuántica , las desviaciones de la invariancia de Lorentz (posiblemente derivadas de esos modelos) vuelven a ser el objetivo de los experimentalistas. Dado que la "invariancia local de Lorentz" (LLI) también se cumple en sistemas de caída libre, los experimentos relacionados con el principio de equivalencia débil también pertenecen a esta clase de pruebas. Los resultados se analizan mediante teorías de prueba (como se mencionó anteriormente) como RMS o, más importante, mediante SME. [3]
{{cite book}}: CS1 maint: multiple names: authors list (link)