
En la rama de las matemáticas conocida como geometría euclidiana , el teorema de Poncelet-Steiner es uno de varios resultados relacionados con construcciones con compás y regla que tienen restricciones adicionales impuestas a las reglas tradicionales. Este resultado establece que todo lo que se puede construir con regla y compás juntos se puede construir solo con regla, siempre que se den un solo círculo y su centro . Este teorema está relacionado con la equivalencia de la brújula oxidada .
Aunque una brújula puede facilitar significativamente las construcciones, se da a entender que no tiene ningún propósito funcional una vez que se ha dibujado el primer círculo. Todas las construcciones siguen siendo posibles, aunque se comprende naturalmente que los círculos y sus arcos no se pueden dibujar sin el compás. Todos los puntos que definen de forma única una construcción, que pueden determinarse con el uso del compás, son igualmente determinables sin ella, aunque con mayor dificultad.
Esto significa únicamente que la brújula se puede utilizar con fines estéticos , más que con fines de construcción. En otras palabras, el compás se puede utilizar después de que se hayan determinado todos los puntos clave, para "rellenar" los arcos con fines puramente visuales o artísticos, si es deseable, y no como un paso necesario hacia la construcción. No se pierde nada por descuidar la construcción de arcos circulares.
Las construcciones realizadas de acuerdo con este teorema (basándose únicamente en el uso de una regla sin la ayuda de un compás) se conocen como construcciones Steiner . Las construcciones de Steiner pueden incluir cualquier número de círculos, incluido ninguno, ya dibujados en el plano, con o sin sus centros. También pueden involucrar todo tipo de formas y curvas únicas preexistentes en el plano, siempre que la herramienta de regla sea la única herramienta física a disposición de los geómetras. Mientras que el teorema de Poncelet-Steiner estipula la existencia de un círculo y su centro, y afirma que un solo círculo equivale a un compás.

En el siglo X, el matemático persa Abu al-Wafa' Buzjani (940-998) consideró construcciones geométricas utilizando una regla y un compás con una abertura fija, el llamado compás oxidado . Las construcciones de este tipo parecían tener cierta importancia práctica, ya que fueron utilizadas por los artistas Leonardo da Vinci y Alberto Durero en Europa a finales del siglo XV. A mediados del siglo XVI se desarrolló un nuevo punto de vista, cuando el tamaño de la abertura se consideraba fijo pero arbitrario y la cuestión de cuántas de las construcciones de Euclides podían obtenerse era primordial. [1]
El matemático renacentista Lodovico Ferrari , alumno de Gerolamo Cardano en un "desafío matemático" contra Niccolò Fontana Tartaglia pudo demostrar que "todo Euclides" (es decir, las construcciones con regla y compás en los primeros seis libros de los Elementos de Euclides ) podrían ser logrado con una regla y un compás oxidado. En diez años, Cardano, Tartaglia y el alumno de Tartaglia, Benedetti, obtuvieron conjuntos adicionales de soluciones. Durante el siglo siguiente, estas soluciones fueron generalmente olvidadas hasta que, en 1673, Georg Mohr publicó (anónimamente y en holandés) Euclidis Curiosi que contenía sus propias soluciones. Mohr sólo había oído hablar de la existencia de los resultados anteriores y esto le llevó a trabajar en el problema. [2]
Demostrar que "todo Euclides" se puede realizar con regla y compás oxidado no es lo mismo que demostrar que todas las construcciones con regla y compás se pueden hacer con regla y sólo un compás oxidado. Tal prueba requeriría la formalización de lo que una regla y un compás podrían construir. Esta base fue proporcionada por Jean Victor Poncelet en 1822, motivado por el trabajo de Mohr sobre el teorema de Mohr-Mascheroni . También conjeturó y sugirió una posible prueba de que una regla y un compás oxidados serían equivalentes a una regla y un compás y, además, el compás oxidado solo debía usarse una vez. El resultado de que " una regla y un círculo con un centro dado equivalen a una regla y un compás " fue demostrado por Jakob Steiner en 1833. [3] [1]
Varias otras nociones, herramientas, terminología, etc., a menudo se asocian (a veces de manera vaga) al teorema de Poncelet-Steiner. Algunos se enumeran aquí.
El término construcción Steiner generalmente se refiere a cualquier construcción geométrica que utiliza solo la herramienta regla y, a veces, se la denomina simplemente construcción solo con regla . No se hacen estipulaciones sobre qué objetos geométricos ya existen en el plano o su ubicación relativa; Cualquiera de estas condiciones se postula con antelación. Además, no se hacen implicaciones sobre lo que es o no posible construir.
Por lo tanto, todas las construcciones que se adhieren al teorema de Poncelet-Steiner son construcciones de Steiner, aunque no todas las construcciones de Steiner cumplen con la condición de un solo círculo con su centro en el plano. El teorema de Poncelet-Steiner no requiere una brújula real; se supone que el círculo preexiste en el plano; por lo tanto, todas las construcciones aquí que demuestran el teorema de Poncelet-Steiner son construcciones de Steiner.
La brújula oxidada describe una brújula cuya bisagra está tan oxidada que se fusiona de tal manera que sus patas (la aguja y el lápiz) no pueden ajustar el ancho. En esencia, se trata de una brújula cuya distancia es fija, y que traza círculos de un radio predeterminado y constante, pero arbitrario. Se pueden dibujar círculos centrados en cualquier punto arbitrario, pero el radio no se puede cambiar.
Como paradigma constructivo restringido , las construcciones con compás oxidado permiten el uso de regla y compás de ancho fijo. La equivalencia de la brújula oxidada:
Naturalmente, se entiende que la brújula de radio arbitrario puede utilizarse con fines estéticos; Para la construcción sólo se podrá utilizar el arco del compás de ancho fijo.
En cierto sentido, la brújula oxidada es una generalización y simplificación del teorema de Poncelet-Steiner. Aunque no es más potente, ciertamente es más conveniente. El teorema de Poncelet-Steiner requiere que se coloque en el plano un solo círculo con radio y punto central arbitrarios. Como es el único círculo dibujado, si fue dibujado o no con un compás oxidado es irrelevante y equivalente. Sin embargo, el beneficio de las construcciones generales con brújula oxidada es que la brújula se puede usar repetidamente para volver a dibujar círculos centrados en cualquier punto deseado, aunque con el mismo radio, simplificando así muchas construcciones. Naturalmente, si todas las construcciones son posibles con un solo círculo colocado arbitrariamente en el plano, entonces seguramente se puede decir lo mismo de una regla y un compás oxidados, con los que se puede colocar al menos un círculo arbitrariamente.
Se sabe que una regla y un compás oxidado son suficientes para construir todo lo que es posible con una regla y un compás estándar, con el entendimiento implícito de que no se pueden dibujar arcos circulares de radios arbitrarios, y sólo es necesario dibujarlos con fines estéticos y no constructivos. . Históricamente esto se demostró cuando se demostró el teorema de Poncelet-Steiner, que es un resultado más sólido. La brújula oxidada, por tanto, no es más débil que el teorema de Poncelet-Steiner. La brújula oxidada tampoco es más fuerte.
El teorema de Poncelet-Steiner reduce la equivalencia de la brújula oxidada de Ferrari, una afirmación en ese momento, a una brújula de un solo uso:
El teorema de Poncelet-Steiner toma el escenario de la brújula oxidada y la rompe por completo después de su primer uso.
Si sólo se va a dar un círculo y ninguna otra información especial, el teorema de Steiner implica que se debe proporcionar el centro del círculo junto con el arco del círculo. Esto se hace demostrando la imposibilidad de construir el centro del círculo solo con una regla usando un solo círculo en el plano, sin su centro. Se utiliza un argumento que utiliza transformaciones proyectivas y las secciones cónicas de Steiner .
También atribuido a David Hilbert y conocido como Error de Hilbert , un resumen ingenuo de la prueba es el siguiente. Con el uso de una herramienta de regla, sólo son posibles transformaciones proyectivas lineales, y las transformaciones proyectivas lineales son operaciones reversibles. Las líneas se proyectan sobre líneas bajo cualquier transformación proyectiva lineal, mientras que las secciones cónicas se proyectan sobre secciones cónicas bajo una transformación proyectiva lineal, pero estas últimas están sesgadas de tal manera que las excentricidades , focos y centros de los círculos no se conservan. Bajo diferentes secuencias de mapeos, el centro no se mapea de manera única y reversible . Este no sería el caso si se pudieran usar líneas para determinar el centro de un círculo. Como las transformaciones lineales son operaciones reversibles y, por lo tanto, producirían resultados únicos, el hecho de que no sean posibles resultados únicos implica la imposibilidad de construcciones de puntos centrales. La singularidad del centro construido dependería de información adicional que haga que la construcción sea reversible.
Por lo tanto, no es posible construir todo lo que se puede construir con regla y compás sólo con regla. En consecuencia, los requisitos del teorema de Poncelet-Steiner no pueden debilitarse con respecto al centro del círculo. Si no se proporciona el centro del único círculo dado, no se puede obtener solo con una regla. Muchas construcciones son imposibles sólo con regla. Es necesario algo más y basta con un círculo con su centro identificado.
Alternativamente, se podrá omitir el centro con suficiente información adicional. Esto no es un debilitamiento del teorema de Poncelet-Steiner, sino simplemente un marco alternativo. Tampoco es una contradicción con el teorema de Steiner, que plantea la hipótesis de un único círculo. La inclusión de esta información alternativa suficiente, que siempre incluye al menos dos círculos, elimina la ambigüedad de las asignaciones bajo las transformaciones proyectivas, permitiendo así que varias construcciones de Steiner recuperen el centro del círculo.
Cada una de estas alternativas requiere al menos dos círculos desprovistos de sus centros, además de alguna otra información única. Algunas alternativas incluyen dos círculos concéntricos o dos círculos que se cruzan, o tres círculos, u otras variaciones en las que los círculos proporcionados carecen de sus centros. En cada uno de ellos se cumple algún criterio adicional único pero suficiente, como por ejemplo concentricidad, puntos de intersección, un tercer círculo, etc., respectivamente. En cualquiera de estos casos, se puede construir el centro de un círculo, reduciendo así el problema a la hipótesis del teorema de Poncelet-Steiner (con la conveniencia adicional de tener círculos adicionales en el plano, cuyos centros ahora se pueden construir).
Para probar el teorema, es necesario demostrar que cada una de las construcciones básicas de compás y regla es posible usando una regla sola (siempre que exista un círculo y su centro en el plano), ya que estos son los fundamentos o pasos elementales. para todas las demás construcciones. Es decir, todas las construcciones se pueden escribir como una serie de pasos que involucran estas cinco construcciones básicas:
#1 – Una línea que pasa por dos puntos
Esto se puede hacer sólo con una regla. No se requiere ni un compás ni un círculo.
#2 – Un círculo que pasa por un punto con centro definido
Se entiende que el arco de un círculo no se puede trazar sin compás. Se considera que un círculo está formado por dos puntos cualesquiera, uno que define el centro y otro que existe en la circunferencia en el radio. Cualquier par de estos define un círculo único, aunque lo contrario no es cierto: para cualquier círculo dado no existe un par único que lo defina. De acuerdo con la intención del teorema que pretendemos demostrar, no es necesario trazar el círculo real salvo por razones estéticas.
#3 – Intersección de dos líneas
Esta construcción también se puede realizar directamente con regla.
#4, #5 – Intersecciones que involucran el círculo
Por lo tanto, para demostrar el teorema, solo es necesario demostrar que las construcciones 4 y 5 son posibles usando solo una regla y un círculo dado con su centro.
Usabilidad
La demostración constructiva no sirve simplemente como prueba del teorema, sino que también demuestra la aplicación práctica de las construcciones más básicas, de modo que la afirmación de constructibilidad con regla podría aplicarse en la práctica, en el caso más general. Dado que todas las construcciones geométricas se pueden expresar como una secuencia de los cinco pasos constructivos básicos, y las siguientes construcciones demuestran y justifican cada uno de ellos, necesariamente, para demostrar el teorema, todas las construcciones posibles pueden implementarse en consecuencia.
Dudas sobre las Construcciones #1, #2 o #3
Cualquier duda sobre las construcciones 1 o 3 se aplicaría igualmente al paradigma de construcción tradicional que involucra la brújula y, por lo tanto, no son preocupaciones exclusivas del teorema de Poncelet-Steiner.
La construcción número 2 no debería ser motivo de preocupación. Aunque es indiscutible que un círculo único está definido por un punto central y un punto en su circunferencia, la pregunta pertinente es si esta es información suficiente para los propósitos de la construcción, o si se requiere el arco dibujado. El arco del círculo sólo se utiliza en paradigmas de construcción tradicionales para fines de intersecciones círculo-círculo y círculo-línea, en ellos el arco del círculo se utiliza directamente para identificar puntos de intersección. Por lo tanto, si las construcciones n.° 4 y n.° 5 son satisfactorias sin el arco del círculo con el cual intersectarse, entonces se demostrará que no es necesario dibujar el arco. Por lo tanto, esto implicaría que la construcción n.° 2 se cumple con un simple etiquetado de dos puntos, identificando el círculo único.
Nomenclatura circular
En las construcciones siguientes, un círculo definido por un punto central P y un punto de su circunferencia, Q , a través del cual pasa el arco del círculo, se denota como P(Q) . Como la mayoría de los círculos no se dibujan con un compás, los puntos del centro y la circunferencia se nombran explícitamente. El arco, si se dibuja, también puede tener un nombre, como por ejemplo círculo c . Según el teorema, cuando se proporciona un círculo dibujado con un compás, simplemente se lo denomina círculo dado o círculo proporcionado .
Generalidad del círculo
Siempre se debe suponer que el círculo proporcionado está colocado arbitrariamente en el plano con un radio arbitrario. Muchos ejemplos de constructibilidad con regla que se pueden encontrar en varias referencias dentro y fuera de línea, supondrán que el círculo no está colocado en la posición general . En cambio, por ejemplo, la constructibilidad de un polígono puede postular que el círculo es circunscrito . Tales supuestos simplifican una construcción pero no prueban la generalidad de la afirmación de constructibilidad. A los efectos de este teorema, podemos suponer que el círculo es, en efecto, completamente general.
Uso del arco de los círculos proporcionados
Los puntos de intersección entre cualquier línea y el círculo dado se pueden encontrar directamente, al igual que los puntos de intersección entre los arcos de dos círculos, si se proporcionan. El teorema de Poncelet-Steiner no prohíbe el tratamiento normal de círculos ya dibujados en el plano; Se aplican las reglas de construcción normales. El teorema sólo prohíbe la construcción de nuevos arcos circulares con un compás.
Colocación de puntos arbitrarios
Las construcciones de Steiner y aquellas construcciones que aquí demuestran el teorema de Poncelet-Steiner requieren la ubicación arbitraria de puntos en el espacio. Estas construcciones se basan en el concepto de puntos fijos, donde la construcción resultante es independiente de la arbitrariedad empleada durante la construcción. En algunos paradigmas de construcción, como en la definición geométrica del número construible , la colocación arbitraria de puntos puede estar prohibida. La geometría tradicional no tiene tal restricción en cuanto a la ubicación de los puntos; con tal restricción contra la colocación de puntos arbitrarios, el círculo único es de hecho más débil que el compás. Sin embargo, esto se puede conciliar. Las construcciones de Steiner pueden usarse como base para el conjunto de números construibles si solo se ingresan en el conjunto aquellos puntos que son fijos, sin tener en cuenta los puntos colocados arbitrariamente necesarios durante una construcción.
Elección de la construcción entre variantes.
En las construcciones generales suele haber varias variaciones que producirán el mismo resultado. Las elecciones realizadas en dicha variante pueden realizarse sin pérdida de generalidad . Sin embargo, cuando se utiliza una construcción para demostrar que se puede hacer algo, no es necesario describir todas estas opciones y, en aras de la claridad de la exposición, a continuación sólo se dará una variante. Las variantes elegidas a continuación se hacen por su ubicuidad y generalización en la aplicación más que por su simplicidad o conveniencia bajo un conjunto particular de condiciones especiales.
Generalidad y simplicidad
Algunos objetivos constructivos específicos, como por ejemplo la construcción de una plaza, pueden tener soluciones constructivas relativamente sencillas, que a pesar de su simplicidad no se mostrarán aquí en el artículo. La omisión de tales construcciones mitiga la extensión del artículo. El propósito de estas decisiones es que tales construcciones pueden no ser ubicuas o suficientemente útiles, particularmente para demostrar el teorema. Aunque el teorema y las construcciones aquí encontradas se pueden utilizar para construir cualquier figura, no se afirma la existencia de alternativas más simples (sólo con regla) para ninguna construcción específica.
A continuación se muestra la demostración del teorema y construcciones útiles basadas únicamente en regla.
Para probar las construcciones #4 y #5 anteriores, que se incluyen a continuación, también se explican a continuación algunas construcciones intermedias necesarias, ya que se utilizan y se hace referencia a ellas con frecuencia. Estas también son construcciones con regla únicamente. Todas las construcciones a continuación se basan en las construcciones básicas n.° 1, n.° 2, n.° 3 y cualquier otra construcción enumerada anteriormente.

Esta construcción no requiere el uso del círculo dado. Naturalmente, cualquier línea que pase por el centro del círculo dado tiene implícitamente un segmento bisectado : el diámetro es bisectado por el centro. El archivo GIF animado incluido en la introducción de este artículo demuestra esta construcción, basándose en el diámetro dividido; nunca se utiliza el arco del círculo, lo cual se reitera aquí sin el círculo y con pasos enumerados.
Dada una recta arbitraria n (en negro) en la que existen dos puntos A y B , que tienen un punto medio M entre ellos, y un punto arbitrario P en el plano (que se supone no está en la recta n ) a través del cual pasa un paralelo de la recta n se debe realizar:
En alguna literatura, el segmento de línea bisecado a veces se ve como un "círculo" unidimensional que existe en la línea. Alternativamente, alguna literatura considera el segmento de línea bisectado como un círculo bidimensional en un espacio tridimensional con la línea pasando por un diámetro, pero no paralela al plano, intersectando así el plano de construcción en dos puntos de la circunferencia con el punto medio simplemente siendo el centro del círculo prescrito.
Esta construcción es un caso especial de la construcción armónica proyectiva conjugada , que no se demuestra en este artículo.
Si la línea pasa por el centro de un círculo, el segmento definido por el diámetro que pasa por el círculo es bisectado por el centro del círculo. En el caso general, sin embargo, cualquier otra línea en el plano puede tener un segmento bisectado construido sobre ella. Esta construcción requiere el uso del círculo dado.
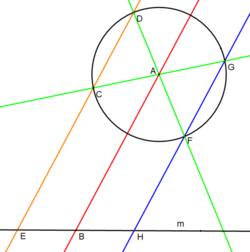
Dada una línea, m (en negro), y un círculo centrado en A , deseamos crear puntos E , B y H en la línea de modo que B sea el punto medio:
Como el punto C se elige arbitrariamente, no es necesario que esté en la perpendicular de la línea AB que pasa por el centro del círculo. Sin embargo, si es así, la línea CD es simplemente la línea tangente al círculo que pasa por el punto C , que coincide con el punto D. Esta construcción es posible aunque no figura en este artículo. Los puntos F y G pueden construirse como antes y también serán iguales entre sí. Y nuevamente, la línea GF es simplemente la línea tangente al círculo en ese punto. Así, los puntos E , H y su punto medio B se pueden encontrar, como antes, con sólo un pequeño cambio añadiendo una subconstrucción.
Esta construcción requiere el uso del círculo dado. Para generalizar la construcción de líneas paralelas a todas las líneas posibles, no solo a aquellas con un segmento de línea bisecado colineal , es necesario tener información adicional. De acuerdo con el teorema de Poncelet-Steiner, el objeto elegido para esta construcción es un círculo (con centro).
Para construir una recta paralela a cualquier recta dada, que pasa por cualquier punto del plano, combinamos trivialmente dos construcciones:
En construcciones alternativas, que no se demuestran en este artículo, se puede construir un paralelo a partir de cualquier par de líneas que ya sean paralelas entre sí; así, a partir de dos cualesquiera se puede producir un tercer paralelo, sin necesidad de utilizar un círculo. Además, se podrá construir una paralela de cualquier recta siempre que exista en el plano cualquier paralelogramo , también sin utilizar una circunferencia determinada.

Esta construcción requiere el uso del círculo dado y aprovecha el teorema de Tales .
A partir de una recta dada m y de un punto A dado en el plano, se construye una perpendicular a la recta que pasa por el punto. Se proporciona el círculo dado O(r) .
Si la línea a partir de la cual se va a trazar una perpendicular pasa por el centro del círculo, un enfoque alternativo sería construir las líneas tangentes al círculo en los puntos de intersección de las líneas, utilizando construcciones de Steiner. Esto no se demuestra en este artículo.
Otra opción en caso de que la línea pase por el centro del círculo sería construir una paralela a ella a través del círculo en un punto arbitrario. Un trapezoide isósceles (o potencialmente un triángulo isósceles) está formado por los puntos de intersección del círculo de ambas líneas. cuyos dos lados no paralelos pueden extenderse hasta un punto de intersección entre ellos, y desde allí trazarse una línea que pase por el centro del círculo. Esta línea es perpendicular y el diámetro es bisectado por el centro.
Mediante una construcción alternativa no demostrada en este artículo, se puede construir una perpendicular de cualquier línea sin círculo, siempre que exista en el plano algún cuadrado .

Dado es un segmento de línea AB , que se va a bisecar. Opcionalmente, existe una línea paralela m en el plano.
Para mayor perspectiva, en cierto sentido esta construcción es una variante de una construcción previa de un paralelo a partir de un segmento de línea bisectado y, por lo tanto, también es un caso especial del conjugado armónico proyectivo (no proporcionado en este artículo). Es el mismo conjunto de líneas tomadas en su conjunto, pero construidas en un orden diferente y a partir de un conjunto inicial diferente de condiciones, llegando a un objetivo final diferente.
Dado que cualquier segmento arbitrario de una de dos rectas paralelas se puede bisecar, y cualquier recta con un segmento bisecado puede tener un paralelo construido, los dos escenarios son proposiciones geométricamente equivalentes. Se implican unos a otros; una construcción simple puede convertir un escenario en otro sin necesidad de información adicional.
En una construcción alternativa, cualquier segmento de línea puede bisecarse siempre que exista un paralelogramo en el plano.
Para definir un círculo sólo se requiere el centro y un punto (cualquier punto) de la circunferencia. En principio , se construye un nuevo punto B' de modo que el círculo A(B) sea igual al círculo A(B') , aunque el punto B no sea igual al punto B' . En esencia, el segmento AB se gira alrededor del punto del eje A , hacia AB' , para un conjunto diferente de puntos definitorios para el mismo círculo.

Una forma de hacerlo que satisface la mayoría de las condiciones es la siguiente:
Esta construcción fallará si la rotación deseada es diametralmente opuesta al círculo (es decir, una rotación de semicírculo). Una solución a este escenario es emplear dos construcciones de rotación separadas, ninguna de las cuales es una rotación de semicírculo respecto de la anterior, sino que una actúa como paso intermedio. Elija cualquier ángulo de rotación arbitrariamente, complete la rotación, luego elija el ángulo suplementario y realice la rotación por segunda vez.
Existe una segunda solución constructiva alternativa de rotación, basada en proyecciones y puntos de perspectiva. Aunque evita la complicación de la rotación en semicírculo antes mencionada, tiene sus propias complicaciones, que se resuelven de manera similar con construcciones de rotación intermedia. La construcción no es más versátil. No se demuestra en este artículo.

Esta construcción requiere el uso del círculo dado (que no está representado) para las subconstrucciones a las que se hace referencia y que se demostraron previamente.
Supongamos que dos círculos A ( B ) y C ( D ) están dados implícitamente, definidos sólo por los puntos A , B , C y D en el plano, con sus centros definidos, pero no están construidos con una brújula. El eje radical , línea m (en azul oscuro), entre los dos círculos se puede construir:
En el caso de que la construcción del eje radical falle debido a que no existe un punto de intersección X entre las líneas paralelas j y k , lo que resulta de la colocación coincidente del punto medio M en la línea AC , se requiere un enfoque alternativo. Uno de esos enfoques es rotar el segmento AB alrededor del punto del eje A (el centro del círculo A ( B ) ). Una vez alcanzada la rotación arbitraria AB' , que define el mismo círculo, la construcción del eje radical puede comenzar de nuevo sin problemas.

Esta construcción requiere el uso del círculo proporcionado, O ( r ) . Cualquier línea puede intersectarse naturalmente con cualquier círculo dibujado con un compás.
Se da la línea m (en negro) y el círculo P(Q) , que no está construido con un compás. Los puntos de intersección del círculo P(Q) y la recta m , que son los puntos A y B , se pueden construir:
La intersección entre dos círculos se convierte en una combinación trivial de dos construcciones anteriores:
La segunda construcción básica, que describe un círculo completo con sólo dos puntos definitorios, nunca necesitó que se construyera un arco con el compás para poder utilizar el círculo en las construcciones. Es decir, las intersecciones de círculos tanto con círculos como con líneas, que en conjunto son la esencia de todas las construcciones que involucran un círculo, se pueden lograr sin el arco. Por lo tanto, definir un círculo por su centro y por cualquier punto arbitrario de su circunferencia es suficiente para describir completamente el círculo completo y construir con él. Como tal, el arco sólo tiene un propósito estético. La construcción básica n.° 2 está satisfecha.
Dado que se ha demostrado que las cinco construcciones básicas se pueden lograr sólo con una regla, siempre que se coloque un solo círculo con su centro en el plano, esto demuestra el teorema de Poncelet-Steiner.
Aunque es un tema distinto por derecho propio, muchos de los conceptos de geometría proyectiva se aplican aquí a las construcciones de Steiner. Jean-Victor Poncelet contribuyó de manera importante al tema cuando postuló el teorema de este artículo, que Jakob Steiner demostró más tarde. Muchos de los conceptos relacionados desarrollados en geometría proyectiva incluyen, entre otros: concurrencia, "puntos en el infinito", perspectiva, razones y razones cruzadas, puntos estables o fijos de involuciones, invariantes, homogeneidad, transformaciones lineales, armónicos proyectivos y otros. . Un tratamiento exhaustivo de las construcciones de Steiner y sus demostraciones requiere conocimientos de geometría proyectiva, aunque el tema de la geometría proyectiva no se limita a las construcciones con regla únicamente.
El teorema de Poncelet-Steiner se puede contrastar con el teorema de Mohr-Mascheroni , que establece que cualquier construcción con compás y regla se puede realizar con sólo un compás. La regla no es necesaria sino por motivos estéticos; No se necesita nada más en el avión.
La restricción de la brújula oxidada permite el uso de un compás y una regla, siempre que la brújula produzca círculos de radio fijo. Aunque las construcciones con brújula oxidada se exploraron desde el siglo X, y se demostró que todo Euclides se podía construir con una brújula oxidada en el siglo XVII, el teorema de Poncelet-Steiner demuestra que el compás y la regla oxidados juntos son más que suficientes para cualquier cosa y toda construcción euclidiana. De hecho, el compás oxidado se convierte en una herramienta que simplifica las construcciones en lugar de simplemente una regla y un círculo único. Visto desde el otro lado, el teorema de Poncelet-Steiner no sólo fija el ancho de la brújula oxidada, sino que garantiza que la brújula se rompa después de su primer uso.
El teorema de equivalencia de la brújula demuestra que la brújula rígida (también llamada brújula moderna), aquella que mantiene su separación cuando se levanta del avión, es equivalente a la brújula colapsable tradicional (también llamada divisoria), aquella que no conserva su separación, por lo que "puesta a cero", cada vez que se levanta del avión. Euclides demostró que la capacidad de transferir distancias (es decir, construir círculos congruentes), una operación que se vuelve trivial con la brújula rígida, era posible con la brújula colapsable. De hecho, se puede hacer utilizando sólo el compás plegable, sin la herramienta regla. En consecuencia, el compás rígido y el compás plegable son equivalentes; lo que puede ser construido por uno puede ser construido por el otro, incluso en el paradigma de construcción basado únicamente en una brújula.
El requisito impuesto al teorema de Poncelet-Steiner (que exista un círculo con su centro en el plano) se ha generalizado o reforzado desde entonces para incluir condiciones alternativas pero igualmente restrictivas.
Sin duda, existen otros escenarios únicos además de los enumerados aquí. Esta no es una lista exhaustiva de posibilidades.
En dos de estas alternativas, el centro puede omitirse por completo siempre que se den dos círculos concéntricos o dos círculos distintos que se cruzan, de los cuales hay dos casos: dos puntos de intersección y un punto de intersección (círculos tangenciales). A partir de cualquiera de estos escenarios se pueden construir centros, reduciendo el escenario a la hipótesis original. Estos no contradicen el teorema de Steiner que, aunque es absolutamente necesario establecer un centro, también plantea la hipótesis de que sólo existe un círculo.
Aún existen otras variaciones. Es suficiente tener dos círculos no concéntricos y que no se intersectan (sin sus centros), siempre que se dé al menos un punto en la línea central que los pasa o en el eje radical entre ellos, o que se proporcionen dos líneas paralelas cualesquiera en el círculo. avión. Alternativamente también es suficiente tener tres círculos que no se crucen. [4] Una vez que se construye un solo centro, el escenario se reduce nuevamente a la hipótesis original del teorema de Poncelet-Steiner.
En cada uno de estos escenarios, existe más información que sólo un segundo círculo. El hecho de que dos círculos sean concéntricos, o que dos círculos tengan puntos de intersección conocidos, o la presencia de un tercer círculo, o de un punto en una línea central o en un eje radical, constituye una información adicional más allá de la mera presencia de un segundo círculo.
En otra alternativa, no se requiere en absoluto el círculo completo. En 1904, Francesco Severi demostró que cualquier pequeño arco (del círculo), junto con el centro, era suficiente. [5] Esta construcción rompe el compás oxidado en cualquier punto antes de que se complete el primer círculo, pero después de haber comenzado, dibujando así una porción continua del arco del círculo en el plano, y aún así todas las construcciones siguen siendo posibles. Por tanto, las condiciones que plantean la hipótesis del teorema de Poncelet-Steiner pueden debilitarse, pero sólo con respecto a la integridad del arco circular y no, según el teorema de Steiner, con respecto al centro.
El teorema demuestra la construcción de Steiner de los puntos de intersección entre una línea y el círculo de un arco, independientemente del tamaño o la posición del arco, utilizando sólo una regla y el arco. La construcción, además, no hace uso del centro del círculo del arco. Aunque se requiere el centro para completar todo Euclides, como lo demuestran el teorema de Steiner y el teorema de Poncelet-Steiner, el centro no es necesario para cruzar una línea con el círculo de ese arco. Usando esta construcción, el arco y el centro del círculo del arco, todas las construcciones de Poncelet-Steiner anteriores se pueden lograr igualmente, aunque con mayor dificultad.
Además, en cada uno de los escenarios mencionados anteriormente en los que se omite el centro del círculo, la integridad del arco circular no es necesaria, según el teorema de Severi, siempre que las intersecciones de los círculos se den explícitamente siempre que no existan arcos de los círculos donde se cruzan. los puntos lo hacen. Es decir, si los puntos de intersección entre dos círculos de arcos no se pueden encontrar directamente a través de los dos arcos, se deben proporcionar. De lo contrario, la integridad del arco circular es redundante.
En lugar de restringir aún más las normas de construcción, es igualmente interesante estudiar la posibilidad de relajar las restricciones. A veces se les llama construcciones extendidas , porque amplían lo que es construible al ampliar el conjunto de herramientas permitido. Estas construcciones también se denominan construcciones neusis (del griego ) porque emplean herramientas distintas al compás y la regla, o construcciones liberadas porque alivian las restricciones del paradigma tradicional.
Así como los geómetras han estudiado qué es posible construir (y cómo) cuando se imponen restricciones adicionales a las reglas de construcción tradicionales (como sólo compás, sólo regla, compás oxidado, etc.), también han estudiado qué construcciones se vuelven posibles que no lo eran. ya cuando se alivien las restricciones naturales inherentes a las reglas de construcción tradicionales. Preguntas como "qué se vuelve construible", "cómo podría construirse", "cuáles son las menos reglas tradicionales que se pueden romper", "cuáles son las herramientas más simples que se necesitan", "qué herramientas aparentemente diferentes son equivalentes", "¿cómo "El nuevo paradigma simplifica las construcciones tradicionales", etc.
El ángulo arbitrario no es trisectable utilizando las reglas tradicionales de compás y regla, por ejemplo, pero la trisección se vuelve construible cuando se permite la herramienta adicional de una elipse en el plano, que en sí misma no es construible. Algunos de los problemas tradicionales no resueltos, como la trisección de ángulos, la duplicación del cubo , la cuadratura del círculo , la búsqueda de raíces cúbicas, etc., que resultaron imposibles únicamente con la regla y el compás, se han resuelto utilizando un conjunto ampliado de herramientas. En general, los objetos estudiados para ampliar el alcance de lo construible han incluido:
Los geómetras antiguos consideraban ideales y preferidas las construcciones con compás y regla (conocidas como construcciones planas ). En segundo lugar, preferían las construcciones sólidas , que incluían el uso de secciones cónicas en el plano distinto del círculo. En tercer lugar, favorecían el uso de curvas suaves y arbitrarias en el avión, y menos aún el uso de neuseis (herramientas físicas portátiles alternativas). Es dudoso que los geómetras antiguos, al menos los del mundo occidental, siquiera consideraran el plegado del papel.
El término neusis o construcción de neusis también puede referirse a una herramienta o método específico empleado por los geómetras antiguos.
La regla graduada es única porque define una métrica y da lugar al tratamiento algebraico de la geometría , la representación gráfica cartesiana e importa una unidad estándar para la proporcionalidad de segmentos.
Vale la pena señalar que en todos los paradigmas de construcción, la regla implícita es que todas las construcciones deben terminar en un número finito de aplicaciones de las herramientas disponibles (brújula y regla) y producir los resultados exactos deseados. Se podrían entablar discusiones enteras con cualquiera de estas condiciones aliviadas.
Para cualquier figura que de otra manera no se pueda construir:
Por ejemplo, una trisección de ángulos se puede realizar exactamente usando una secuencia infinita de bisecciones de ángulos. Si la construcción termina en alguna iteración finita, se puede lograr una aproximación precisa de una trisección con precisión arbitraria. Aunque cada punto, línea o círculo es una construcción válida, lo que pretende aproximar nunca puede lograrse realmente en aplicaciones finitas de un compás y/o regla.
Por supuesto, existen figuras exactamente construibles que son aproximaciones razonables para figuras no construibles, como construcciones relativamente simples y no iterativas para una aproximación del heptágono.