stringtranslate.com

Genética de poblaciones

La genética de poblaciones es un subcampo de la genética que estudia las diferencias genéticas dentro y entre poblaciones y forma parte de la biología evolutiva . Los estudios en esta rama de la biología examinan fenómenos como la adaptación , la especiación y la estructura de las poblaciones . [1]

La genética de poblaciones fue un ingrediente vital en el surgimiento de la síntesis evolutiva moderna . Sus fundadores principales fueron Sewall Wright , JBS Haldane y Ronald Fisher , quienes también sentaron las bases para la disciplina relacionada de la genética cuantitativa . Tradicionalmente una disciplina altamente matemática, la genética de poblaciones moderna abarca trabajo teórico, de laboratorio y de campo. Los modelos genéticos de poblaciones se utilizan tanto para la inferencia estadística a partir de datos de secuencias de ADN como para la prueba/refutación de conceptos. [2]

Lo que distingue a la genética de poblaciones de los enfoques más nuevos y más fenotípicos para modelar la evolución, como la teoría de juegos evolutivos y la dinámica adaptativa , es su énfasis en fenómenos genéticos como la dominancia , la epistasis , el grado en que la recombinación genética rompe el desequilibrio de ligamiento y los fenómenos aleatorios de mutación y deriva genética . Esto la hace apropiada para la comparación con los datos de genómica de poblaciones .

Historia

La genética de poblaciones comenzó como una reconciliación de la herencia mendeliana y los modelos bioestadísticos . La selección natural solo causará evolución si hay suficiente variación genética en una población. Antes del descubrimiento de la genética mendeliana , una hipótesis común era la herencia combinada . Pero con la herencia combinada, la varianza genética se perdería rápidamente, haciendo improbable la evolución por selección natural o sexual. El principio de Hardy-Weinberg proporciona la solución a cómo se mantiene la variación en una población con herencia mendeliana. Según este principio, las frecuencias de los alelos (variaciones en un gen) permanecerán constantes en ausencia de selección, mutación, migración y deriva genética. [3]

El siguiente paso clave fue el trabajo del biólogo y estadístico británico Ronald Fisher . En una serie de artículos que comenzaron en 1918 y culminaron en su libro de 1930 The Genetical Theory of Natural Selection , Fisher demostró que la variación continua medida por los biometristas podría ser producida por la acción combinada de muchos genes discretos, y que la selección natural podría cambiar las frecuencias de los alelos en una población, lo que daría lugar a la evolución. En una serie de artículos que comenzaron en 1924, otro genetista británico, JBS Haldane , elaboró ​​las matemáticas del cambio de frecuencia de los alelos en un solo locus genético bajo una amplia gama de condiciones. Haldane también aplicó el análisis estadístico a ejemplos del mundo real de selección natural, como la evolución de la polilla moteada y el melanismo industrial , y demostró que los coeficientes de selección podrían ser mayores de lo que Fisher suponía, lo que conduce a una evolución adaptativa más rápida como estrategia de camuflaje tras el aumento de la contaminación. [4] [5]

El biólogo estadounidense Sewall Wright , que tenía experiencia en experimentos de cría de animales , se centró en las combinaciones de genes que interactuaban y en los efectos de la endogamia en poblaciones pequeñas y relativamente aisladas que mostraban deriva genética. En 1932, Wright introdujo el concepto de paisaje adaptativo y sostuvo que la deriva genética y la endogamia podían alejar a una subpoblación pequeña y aislada de un pico adaptativo, permitiendo que la selección natural la llevara hacia diferentes picos adaptativos. [ cita requerida ]

El trabajo de Fisher, Haldane y Wright fundó la disciplina de la genética de poblaciones. Esto integró la selección natural con la genética mendeliana, que fue el primer paso crítico para desarrollar una teoría unificada de cómo funcionaba la evolución. [4] [5] John Maynard Smith fue alumno de Haldane, mientras que WD Hamilton estuvo influenciado por los escritos de Fisher. El estadounidense George R. Price trabajó tanto con Hamilton como con Maynard Smith. El estadounidense Richard Lewontin y el japonés Motoo Kimura estuvieron influenciados por Wright y Haldane. [ cita requerida ]

Síntesis moderna

Las matemáticas de la genética de poblaciones se desarrollaron originalmente como el comienzo de la síntesis moderna . Autores como Beatty [6] han afirmado que la genética de poblaciones define el núcleo de la síntesis moderna. Durante las primeras décadas del siglo XX, la mayoría de los naturalistas de campo continuaron creyendo que el lamarckismo y la ortogénesis proporcionaban la mejor explicación para la complejidad que observaban en el mundo viviente. [7] Durante la síntesis moderna, estas ideas fueron depuradas y solo se conservaron las causas evolutivas que podían expresarse en el marco matemático de la genética de poblaciones. [8] Se llegó a un consenso sobre qué factores evolutivos podrían influir en la evolución, pero no sobre la importancia relativa de los diversos factores. [8]

Theodosius Dobzhansky , un trabajador postdoctoral en el laboratorio de TH Morgan , había sido influenciado por el trabajo sobre diversidad genética de genetistas rusos como Sergei Chetverikov . Ayudó a tender un puente entre los fundamentos de la microevolución desarrollados por los genetistas de poblaciones y los patrones de macroevolución observados por los biólogos de campo, con su libro de 1937 Genética y el origen de las especies . Dobzhansky examinó la diversidad genética de las poblaciones silvestres y demostró que, contrariamente a las suposiciones de los genetistas de poblaciones, estas poblaciones tenían grandes cantidades de diversidad genética, con marcadas diferencias entre subpoblaciones. El libro también tomó el trabajo altamente matemático de los genetistas de poblaciones y lo puso en una forma más accesible. Muchos más biólogos fueron influenciados por la genética de poblaciones a través de Dobzhansky de los que pudieron leer los trabajos altamente matemáticos en el original. [9]

En Gran Bretaña, EB Ford , el pionero de la genética ecológica , [10] continuó durante las décadas de 1930 y 1940 demostrando empíricamente el poder de la selección debido a factores ecológicos, incluida la capacidad de mantener la diversidad genética a través de polimorfismos genéticos como los tipos de sangre humanos . El trabajo de Ford, en colaboración con Fisher, contribuyó a un cambio de énfasis durante la síntesis moderna hacia la selección natural como la fuerza dominante. [4] [5] [11] [12]

Teoría neutral y dinámica de fijación del origen

La visión de síntesis original y moderna de la genética de poblaciones supone que las mutaciones proporcionan abundante materia prima y se centra únicamente en el cambio en la frecuencia de los alelos dentro de las poblaciones . [13] Los principales procesos que influyen en las frecuencias de los alelos son la selección natural , la deriva genética , el flujo genético y la mutación recurrente . Fisher y Wright tenían algunos desacuerdos fundamentales sobre los papeles relativos de la selección y la deriva. [14] La disponibilidad de datos moleculares sobre todas las diferencias genéticas condujo a la teoría neutral de la evolución molecular . En esta visión, muchas mutaciones son perjudiciales y, por lo tanto, nunca se observan, y la mayoría del resto son neutrales, es decir, no están bajo selección. Con el destino de cada mutación neutral dejado al azar (deriva genética), la dirección del cambio evolutivo está impulsada por las mutaciones que ocurren, y por lo tanto no puede capturarse solo con modelos de cambio en la frecuencia de los alelos (existentes). [13] [15]

La visión de la fijación del origen de la genética de poblaciones generaliza este enfoque más allá de las mutaciones estrictamente neutrales y considera la tasa a la que ocurre un cambio particular como el producto de la tasa de mutación y la probabilidad de fijación . [13]

Cuatro procesos

Selección

La selección natural , que incluye la selección sexual , es el hecho de que algunos rasgos hacen que sea más probable que un organismo sobreviva y se reproduzca . La genética de poblaciones describe la selección natural definiendo la aptitud como una propensión o probabilidad de supervivencia y reproducción en un entorno particular. La aptitud normalmente se da con el símbolo w = 1- s donde s es el coeficiente de selección . La selección natural actúa sobre los fenotipos , por lo que los modelos genéticos de poblaciones suponen relaciones relativamente simples para predecir el fenotipo y, por lo tanto, la aptitud a partir del alelo en uno o un pequeño número de loci. De esta manera, la selección natural convierte las diferencias en la aptitud de los individuos con diferentes fenotipos en cambios en la frecuencia de los alelos en una población a lo largo de generaciones sucesivas. [ cita requerida ]

Antes de la llegada de la genética de poblaciones, muchos biólogos dudaban de que pequeñas diferencias en la aptitud fueran suficientes para hacer una gran diferencia en la evolución. [9] Los genetistas de poblaciones abordaron esta preocupación en parte comparando la selección con la deriva genética . La selección puede superar la deriva genética cuando s es mayor que 1 dividido por el tamaño efectivo de la población . Cuando se cumple este criterio, la probabilidad de que un nuevo mutante ventajoso se vuelva fijo es aproximadamente igual a 2s . [16] [17] El tiempo hasta la fijación de dicho alelo es aproximadamente . [18]

Dominio

La dominancia significa que el efecto fenotípico y/o de aptitud de un alelo en un locus depende de qué alelo está presente en la segunda copia de ese locus. Consideremos tres genotipos en un locus, con los siguientes valores de aptitud [19]

s es el coeficiente de selección y h es el coeficiente de dominancia. El valor de h arroja la siguiente información:

Epistasis

El logaritmo de la aptitud en función del número de mutaciones deletéreas. La epistasis sinérgica está representada por la línea roja: cada mutación deletérea posterior tiene un efecto proporcionalmente mayor en la aptitud del organismo. La epistasis antagónica está en azul. La línea negra muestra el caso no epistático, donde la aptitud es el producto de las contribuciones de cada uno de sus loci.

La epistasis significa que el efecto fenotípico y/o de aptitud de un alelo en un locus depende de qué alelos están presentes en otros loci. La selección no actúa sobre un solo locus, sino sobre un fenotipo que surge a través del desarrollo a partir de un genotipo completo. [20] Sin embargo, muchos modelos de genética de poblaciones de especies sexuales son modelos de "locus único", donde la aptitud de un individuo se calcula como el producto de las contribuciones de cada uno de sus loci, asumiendo efectivamente que no hay epistasis.

De hecho, el panorama de la relación genotipo-aptitud es más complejo. La genética de poblaciones debe modelar esta complejidad en detalle o capturarla mediante alguna regla de promedio más simple. Empíricamente, las mutaciones beneficiosas tienden a tener un beneficio de aptitud menor cuando se agregan a un trasfondo genético que ya tiene una aptitud alta: esto se conoce como epistasis de rendimientos decrecientes. [21] Cuando las mutaciones deletéreas también tienen un efecto de aptitud menor sobre trasfondos de aptitud alta, esto se conoce como "epstasis sinérgica". Sin embargo, el efecto de las mutaciones deletéreas tiende en promedio a ser muy cercano al multiplicativo, o incluso puede mostrar el patrón opuesto, conocido como "epstasis antagónica". [22]

La epistasis sinérgica es fundamental para algunas teorías sobre la purga de la carga de mutaciones [23] y para la evolución de la reproducción sexual .

Mutación

Drosophila melanogaster

El proceso genético de mutación tiene lugar dentro de un individuo, dando como resultado cambios hereditarios en el material genético. Este proceso a menudo se caracteriza por una descripción de los estados inicial y final, o el tipo de cambio que ha sucedido a nivel de ADN (por ejemplo, una mutación de T a C, una deleción de 1 pb), de genes o proteínas (por ejemplo, una mutación nula, una mutación de pérdida de función), o a un nivel fenotípico más alto (por ejemplo, mutación de ojos rojos). Los cambios de un solo nucleótido son con frecuencia el tipo más común de mutación, pero son posibles muchos otros tipos de mutación , y ocurren a tasas muy variables que pueden mostrar asimetrías o sesgos sistemáticos ( sesgo de mutación ).

Las mutaciones pueden implicar la duplicación de grandes secciones de ADN , generalmente a través de la recombinación genética . [24] Esto conduce a una variación en el número de copias dentro de una población. Las duplicaciones son una fuente importante de materia prima para la evolución de nuevos genes. [25] Otros tipos de mutaciones ocasionalmente crean nuevos genes a partir de ADN previamente no codificante. [26] [27]

En la distribución de los efectos de aptitud (EFA) para las nuevas mutaciones, sólo una minoría de las mutaciones son beneficiosas. Las mutaciones con efectos macroscópicos suelen ser perjudiciales. Los estudios realizados en la mosca Drosophila melanogaster sugieren que si una mutación cambia una proteína producida por un gen, esto probablemente será perjudicial, ya que alrededor del 70 por ciento de estas mutaciones tienen efectos perjudiciales y el resto son neutrales o ligeramente beneficiosos. [28]

Este proceso biológico de mutación se representa en los modelos genéticos de poblaciones de una de dos maneras: como una presión determinista de mutación recurrente sobre las frecuencias de los alelos o como una fuente de variación. En la teoría determinista, la evolución comienza con un conjunto predeterminado de alelos y procede mediante cambios en las frecuencias continuas, como si la población fuera infinita. La ocurrencia de mutaciones en individuos se representa mediante una "fuerza" o "presión" de mutación a nivel de población, es decir, la fuerza de innumerables eventos de mutación con una magnitud escalada u aplicada a frecuencias cambiantes f(A1) a f(A2). Por ejemplo, en el modelo clásico de equilibrio mutación-selección , [29] la fuerza de la presión de mutación empuja la frecuencia de un alelo hacia arriba, y la selección contra sus efectos nocivos empuja la frecuencia hacia abajo, de modo que se alcanza un equilibrio, dado (en el caso más simple) por f = u/s.

Este concepto de presión mutacional es útil principalmente para considerar las implicaciones de la mutación deletérea, como la carga de mutación y sus implicaciones para la evolución de la tasa de mutación. [30] La transformación de poblaciones por presión mutacional es poco probable. Haldane [31]  argumentó que requeriría altas tasas de mutación sin oposición de la selección, y Kimura [32] concluyó aún más pesimistamente que incluso esto era poco probable, ya que el proceso tomaría demasiado tiempo (ver evolución por presión mutacional ).

Sin embargo, la evolución por presión mutacional es posible bajo algunas circunstancias y ha sido sugerida por mucho tiempo como una posible causa para la pérdida de rasgos no utilizados. [33] Por ejemplo, los pigmentos ya no son útiles cuando los animales viven en la oscuridad de las cuevas, y tienden a perderse. [34] Un ejemplo experimental involucra la pérdida de esporulación en poblaciones experimentales de B. subtilis . La esporulación es un rasgo complejo codificado por muchos loci, de modo que la tasa de mutación para la pérdida del rasgo se estimó como un valor inusualmente alto, . [35] La pérdida de esporulación en este caso puede ocurrir por mutación recurrente, sin requerir selección para la pérdida de la capacidad de esporulación. Cuando no hay selección para la pérdida de función, la velocidad a la que evoluciona la pérdida depende más de la tasa de mutación que del tamaño efectivo de la población , [36] lo que indica que está impulsada más por la mutación que por la deriva genética.

El papel de la mutación como fuente de novedad es diferente de estos modelos clásicos de presión mutacional. Cuando los modelos genéticos de población incluyen un proceso dependiente de la tasa de introducción u origen mutacional, es decir, un proceso que introduce nuevos alelos incluyendo los neutrales y beneficiosos, entonces las propiedades de la mutación pueden tener un impacto más directo en la tasa y dirección de la evolución, incluso si la tasa de mutación es muy baja. [37] [38] Es decir, el espectro de mutación puede volverse muy importante, particularmente los sesgos de mutación , diferencias predecibles en las tasas de ocurrencia para diferentes tipos de mutaciones, porque el sesgo en la introducción de variación puede imponer sesgos en el curso de la evolución. [39]

La mutación juega un papel clave en otras teorías clásicas y recientes, incluyendo el trinquete de Muller , la subfuncionalización , el concepto de catástrofe de error de Eigen y la hipótesis de riesgo mutacional de Lynch .

Deriva genética

La deriva genética es un cambio en las frecuencias de los alelos causado por un muestreo aleatorio . [40] Es decir, los alelos en la descendencia son una muestra aleatoria de los de los padres. [41] La deriva genética puede hacer que las variantes genéticas desaparezcan por completo y, por lo tanto, reducir la variabilidad genética. A diferencia de la selección natural, que hace que las variantes genéticas sean más o menos comunes dependiendo de su éxito reproductivo, [42] los cambios debidos a la deriva genética no están impulsados ​​por presiones ambientales o adaptativas, y es igualmente probable que hagan que un alelo sea más común que menos común.

El efecto de la deriva genética es mayor para alelos presentes en pocas copias que cuando un alelo está presente en muchas copias. La genética de poblaciones de la deriva genética se describe utilizando procesos de ramificación o una ecuación de difusión que describe cambios en la frecuencia de los alelos. [43] Estos enfoques se aplican generalmente a los modelos de genética de poblaciones de Wright-Fisher y Moran . Suponiendo que la deriva genética es la única fuerza evolutiva que actúa sobre un alelo, después de t generaciones en muchas poblaciones replicadas, comenzando con frecuencias de alelos de p y q, la varianza en la frecuencia de alelos a través de esas poblaciones es

[44]

Ronald Fisher sostuvo que la deriva genética desempeña, como mucho, un papel menor en la evolución, y esta fue la opinión dominante durante varias décadas. Ninguna perspectiva de la genética de poblaciones le ha dado nunca un papel central a la deriva genética por sí sola, pero algunas han hecho que la deriva genética sea importante en combinación con otra fuerza no selectiva. La teoría del equilibrio cambiante de Sewall Wright sostuvo que la combinación de la estructura de la población y la deriva genética era importante. La teoría neutral de la evolución molecular de Motoo Kimura sostiene que la mayoría de las diferencias genéticas dentro y entre poblaciones son causadas por la combinación de mutaciones neutrales y deriva genética. [45]

El papel de la deriva genética por medio del error de muestreo en la evolución ha sido criticado por John H Gillespie [46] y Will Provine [47] , quienes sostienen que la selección en sitios vinculados es una fuerza estocástica más importante, que realiza el trabajo tradicionalmente atribuido a la deriva genética por medio del error de muestreo. Las propiedades matemáticas del arrastre genético son diferentes de las de la deriva genética. [48] La dirección del cambio aleatorio en la frecuencia de los alelos está autocorrelacionada a lo largo de las generaciones. [40]

Flujo genético

El flujo genético es la transferencia de alelos de una población a otra a través de la inmigración de individuos. En este ejemplo, una de las aves de la población A migra a la población B, que tiene menos alelos dominantes, y mediante el apareamiento incorpora sus alelos a la otra población.

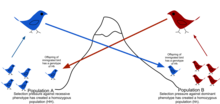
Debido a las barreras físicas a la migración, junto con la tendencia limitada de los individuos a moverse o dispersarse (vagilidad) y la tendencia a permanecer o regresar al lugar natal ( filopatría ), las poblaciones naturales rara vez se cruzan entre sí, como se puede suponer en los modelos aleatorios teóricos ( panmixia ). [49] Por lo general, existe un rango geográfico dentro del cual los individuos están más estrechamente relacionados entre sí que aquellos seleccionados al azar de la población general. Esto se describe como el grado en que una población está estructurada genéticamente. [50]

La Gran Muralla China es un obstáculo para el flujo genético de algunas especies terrestres. [51]

La estructuración genética puede ser causada por la migración debido al cambio climático histórico , la expansión del rango de especies o la disponibilidad actual de hábitat . El flujo genético se ve obstaculizado por cadenas montañosas, océanos y desiertos o incluso estructuras creadas por el hombre como la Gran Muralla China , que ha obstaculizado el flujo de genes de las plantas. [51]

El flujo genético es el intercambio de genes entre poblaciones o especies, rompiendo la estructura. Algunos ejemplos de flujo genético dentro de una especie incluyen la migración y luego la reproducción de organismos, o el intercambio de polen . La transferencia genética entre especies incluye la formación de organismos híbridos y la transferencia genética horizontal . Los modelos genéticos de población se pueden utilizar para identificar qué poblaciones muestran un aislamiento genético significativo entre sí y para reconstruir su historia. [52]

Someter a una población a aislamiento conduce a una depresión endogámica . La migración a una población puede introducir nuevas variantes genéticas, [53] contribuyendo potencialmente al rescate evolutivo . Si una proporción significativa de individuos o gametos migran, también puede cambiar las frecuencias de los alelos, por ejemplo, dando lugar a una carga migratoria . [54]

En presencia de flujo genético, se requieren otras barreras a la hibridación entre dos poblaciones divergentes de una especie exogámica para que las poblaciones se conviertan en nuevas especies .

Transferencia horizontal de genes

Árbol de la vida actual que muestra transferencias genéticas verticales y horizontales

La transferencia horizontal de genes es la transferencia de material genético de un organismo a otro organismo que no es su descendencia; esto es más común entre los procariotas . [55] En medicina, esto contribuye a la propagación de la resistencia a los antibióticos , ya que cuando una bacteria adquiere genes de resistencia puede transferirlos rápidamente a otras especies. [56] También puede haber ocurrido la transferencia horizontal de genes de bacterias a eucariotas, como la levadura Saccharomyces cerevisiae y el escarabajo del frijol adzuki Callosobruchus chinensis . [57] [58] Un ejemplo de transferencias a mayor escala son los rotíferos bdelloides eucariotas , que parecen haber recibido una variedad de genes de bacterias, hongos y plantas. [59] Los virus también pueden transportar ADN entre organismos, lo que permite la transferencia de genes incluso a través de dominios biológicos . [60] También se ha producido una transferencia de genes a gran escala entre los ancestros de las células eucariotas y los procariotas, durante la adquisición de cloroplastos y mitocondrias . [61]

Enlace

Si todos los genes están en equilibrio de ligamiento , el efecto de un alelo en un locus se puede promediar en el acervo genético en otros loci. En realidad, un alelo se encuentra frecuentemente en desequilibrio de ligamiento con genes en otros loci, especialmente con genes ubicados cerca en el mismo cromosoma. La recombinación rompe este desequilibrio de ligamiento demasiado lentamente para evitar el autostop genético , donde un alelo en un locus aumenta a alta frecuencia porque está vinculado a un alelo bajo selección en un locus cercano. El ligamiento también ralentiza la tasa de adaptación, incluso en poblaciones sexuales. [62] [63] [64] El efecto del desequilibrio de ligamiento en la ralentización de la tasa de evolución adaptativa surge de una combinación del efecto Hill-Robertson (demoras en unir mutaciones beneficiosas) y la selección de fondo (demoras en separar las mutaciones beneficiosas de las autoestopistas deletéreas ).

El ligamiento es un problema para los modelos genéticos de poblaciones que tratan un locus genético a la vez. Sin embargo, puede aprovecharse como método para detectar la acción de la selección natural a través de barridos selectivos .

En el caso extremo de una población asexual , el ligamiento es completo y las ecuaciones genéticas de la población se pueden derivar y resolver en términos de una onda viajera de frecuencias de genotipo a lo largo de un paisaje de aptitud simple . [65] La mayoría de los microbios , como las bacterias , son asexuales. La genética de la población de su adaptación tiene dos regímenes contrastantes. Cuando el producto de la tasa de mutación beneficiosa y el tamaño de la población es pequeño, las poblaciones asexuales siguen un "régimen sucesional" de dinámica de fijación del origen, con una tasa de adaptación fuertemente dependiente de este producto. Cuando el producto es mucho más grande, las poblaciones asexuales siguen un régimen de "mutaciones concurrentes" con una tasa de adaptación menos dependiente del producto, caracterizado por la interferencia clonal y la aparición de una nueva mutación beneficiosa antes de que se haya fijado la última .

Aplicaciones

Explicando los niveles de variación genética

La teoría neutral predice que el nivel de diversidad de nucleótidos en una población será proporcional al producto del tamaño de la población por la tasa de mutación neutral. El hecho de que los niveles de diversidad genética varíen mucho menos que los tamaños de las poblaciones se conoce como la "paradoja de la variación". [66] Si bien los altos niveles de diversidad genética fueron uno de los argumentos originales a favor de la teoría neutral, la paradoja de la variación ha sido uno de los argumentos más sólidos en contra de la teoría neutral.

Está claro que los niveles de diversidad genética varían mucho dentro de una especie en función de la tasa de recombinación local, debido tanto a la interacción genética como a la selección de fondo . La mayoría de las soluciones actuales a la paradoja de la variación invocan cierto nivel de selección en sitios vinculados. [67] Por ejemplo, un análisis sugiere que las poblaciones más grandes tienen barridos más selectivos, que eliminan más diversidad genética neutral. [68] Una correlación negativa entre la tasa de mutación y el tamaño de la población también puede contribuir. [69]

La historia de vida afecta la diversidad genética más que la historia de la población, por ejemplo, los estrategas r tienen más diversidad genética. [67]

Detección de selección

Los modelos de genética de poblaciones se utilizan para inferir qué genes están siendo seleccionados. Un enfoque común es buscar regiones de alto desequilibrio de ligamiento y baja varianza genética a lo largo del cromosoma, para detectar barridos selectivos recientes .

Un segundo enfoque común es la prueba de McDonald–Kreitman , que compara la cantidad de variación dentro de una especie ( polimorfismo ) con la divergencia entre especies (sustituciones) en dos tipos de sitios; uno de ellos se supone que es neutral. Normalmente, se supone que los sitios sinónimos son neutrales. [70] Los genes sometidos a selección positiva tienen un exceso de sitios divergentes en relación con los sitios polimórficos. La prueba también se puede utilizar para obtener una estimación de todo el genoma de la proporción de sustituciones que se fijan mediante selección positiva, α. [71] [72] Según la teoría neutral de la evolución molecular , este número debería ser cercano a cero. Por lo tanto, los números altos se han interpretado como una falsificación de la teoría neutral a nivel de todo el genoma. [73]

Inferencia demográfica

La prueba más simple para la estructura de la población en una especie diploide que se reproduce sexualmente es ver si las frecuencias de los genotipos siguen las proporciones de Hardy-Weinberg como una función de las frecuencias de los alelos. Por ejemplo, en el caso más simple de un solo locus con dos alelos denotados A y a en frecuencias p y q , el apareamiento aleatorio predice freq( AA ) =  p 2 para los homocigotos AA , freq( aa ) =  q 2 para los homocigotos aa , y freq( Aa ) = 2 pq para los heterocigotos . En ausencia de estructura de la población, las proporciones de Hardy-Weinberg se alcanzan dentro de 1-2 generaciones de apareamiento aleatorio. Más típicamente, hay un exceso de homocigotos, indicativo de la estructura de la población. La extensión de este exceso se puede cuantificar como el coeficiente de endogamia, F .

Los individuos pueden agruparse en K subpoblaciones. [74] [75] El grado de estructura de la población puede calcularse utilizando F ST , que es una medida de la proporción de varianza genética que puede explicarse por la estructura de la población. La estructura genética de la población puede entonces relacionarse con la estructura geográfica y puede detectarse la mezcla genética .

La teoría coalescente relaciona la diversidad genética de una muestra con la historia demográfica de la población de la que se tomó. Normalmente supone neutralidad , por lo que se seleccionan secuencias de porciones de genomas con una evolución más neutral para dichos análisis. Puede utilizarse para inferir las relaciones entre especies ( filogenética ), así como la estructura de la población, la historia demográfica (por ejemplo , cuellos de botella de la población , crecimiento de la población ), la dispersión biológica , la dinámica fuente-sumidero [76] y la introgresión dentro de una especie.

Otro enfoque para la inferencia demográfica se basa en el espectro de frecuencia de los alelos . [77]

Evolución de los sistemas genéticos

Al suponer que existen loci que controlan el sistema genético en sí, se crean modelos genéticos de población para describir la evolución de la dominancia y otras formas de robustez , la evolución de la reproducción sexual y las tasas de recombinación, la evolución de las tasas de mutación , la evolución de los condensadores evolutivos , la evolución de los rasgos de señalización costosos , la evolución del envejecimiento y la evolución de la cooperación . Por ejemplo, la mayoría de las mutaciones son perjudiciales, por lo que la tasa de mutación óptima para una especie puede ser un equilibrio entre el daño de una alta tasa de mutación perjudicial y los costos metabólicos de mantener sistemas para reducir la tasa de mutación, como las enzimas de reparación del ADN. [78]

Un aspecto importante de estos modelos es que la selección sólo es lo suficientemente fuerte como para purgar las mutaciones deletéreas y, por lo tanto, superar el sesgo mutacional hacia la degradación si el coeficiente de selección s es mayor que el inverso del tamaño efectivo de la población . Esto se conoce como la barrera de deriva y está relacionado con la teoría casi neutral de la evolución molecular . La teoría de la barrera de deriva predice que las especies con grandes tamaños efectivos de población tendrán sistemas genéticos altamente simplificados y eficientes, mientras que aquellas con tamaños de población pequeños tendrán genomas hinchados y complejos que contienen, por ejemplo, intrones y elementos transponibles . [79] Sin embargo, de manera algo paradójica, las especies con grandes tamaños de población podrían ser tan tolerantes a las consecuencias de ciertos tipos de errores que desarrollan tasas de error más altas, por ejemplo, en la transcripción y la traducción , que las poblaciones pequeñas. [80]

Véase también

Referencias

  1. ^ "Genética de poblaciones - Últimas investigaciones y noticias". www.nature.com . Consultado el 29 de enero de 2018 .
  2. ^ Servedio, Maria R. ; Brandvain, Yaniv; Dhole, Sumit; Fitzpatrick, Courtney L.; Goldberg, Emma E.; Stern, Caitlin A.; Van Cleve, Jeremy; Yeh, D. Justin (9 de diciembre de 2014). "No solo una teoría: la utilidad de los modelos matemáticos en la biología evolutiva". PLOS Biology . 12 (12): e1002017. doi : 10.1371/journal.pbio.1002017 . PMC 4260780 . PMID  25489940. 
  3. ^ Ewens, WJ (2004). Genética de poblaciones matemática (2.ª ed.). Nueva York: Springer. ISBN 978-0-387-20191-7.
  4. ^ abc Bowler, Peter J. (2003). Evolución: la historia de una idea (3.ª ed.). Berkeley: University of California Press. pp. 325–339. ISBN 978-0-520-23693-6.
  5. ^ abc Larson, Edward J. (2004). Evolución: la notable historia de una teoría científica (Modern Library ed.). Nueva York: Modern Library. pp. 221–243. ISBN 978-0-679-64288-6.
  6. ^ Beatty, John (1986). "La síntesis y la teoría sintética". Integración de disciplinas científicas . Ciencia y filosofía. Vol. 2. Springer Netherlands. págs. 125-135. doi :10.1007/978-94-010-9435-1_7. ISBN 9789024733422.
  7. ^ Mayr, Ernst ; Provine, William B., eds. (1998). La síntesis evolutiva: perspectivas sobre la unificación de la biología ([Nueva ed.]. ed.). Cambridge, Massachusetts: Harvard University Press. pp. 295–298. ISBN 9780674272262.
  8. ^ ab Provine, WB (1988). "Progreso en la evolución y sentido de la vida". Progreso evolutivo . University of Chicago Press. págs. 49–79.
  9. ^ ab Provine, William B. (1978). "El papel de los genetistas matemáticos de poblaciones en la síntesis evolutiva de los años 1930 y 1940". Estudios de la historia de la biología . 2 : 167–192. PMID  11610409.
  10. ^ Ford, EB (1975) [1964]. Genética ecológica (4ª ed.). Londres: Chapman and Hall. pp. 1ff.
  11. ^ Mayr, Ernst (1988). Hacia una nueva filosofía de la biología: observaciones de un evolucionista . Cambridge, Massachusetts: Belknap Press de Harvard University Press . pág. 402. ISBN. 978-0-674-89665-9.
  12. ^ Mayr, Ernst ; Provine, William B., eds. (1998). La síntesis evolutiva: perspectivas sobre la unificación de la biología ([Nueva ed.]. ed.). Cambridge, Massachusetts: Harvard University Press. pp. 338–341. ISBN 9780674272262.
  13. ^ abc McCandlish, David M.; Stoltzfus, Arlin (septiembre de 2014). "Modelado de la evolución utilizando la probabilidad de fijación: historia e implicaciones". The Quarterly Review of Biology . 89 (3): 225–252. doi :10.1086/677571. PMID  25195318. S2CID  19619966.
  14. ^ Crow, James F. (2010). "Wright y Fisher sobre endogamia y deriva aleatoria". Genética . 184 (3): 609–611. doi : 10.1534/genetics.109.110023 . ISSN  0016-6731. PMC 2845331 . PMID  20332416. 
  15. ^ Casillas, Sònia; Barbadilla, Antonio (2017). "Genética de poblaciones moleculares". Genética . 205 (3): 1003–1035. doi :10.1534/genética.116.196493. PMC 5340319 . PMID  28270526. 
  16. ^ Haldane, JBS (1927). "Una teoría matemática de la selección natural y artificial, parte V: selección y mutación". Actas matemáticas de la Sociedad Filosófica de Cambridge . 23 (7): 838–844. Bibcode :1927PCPS...23..838H. doi :10.1017/S0305004100015644. S2CID  86716613.
  17. ^ Orr, HA (2010). "La genética de poblaciones de mutaciones beneficiosas". Philosophical Transactions of the Royal Society B: Biological Sciences . 365 (1544): 1195–1201. doi :10.1098/rstb.2009.0282. PMC 2871816 . PMID  20308094. 
  18. ^ Hermisson, J.; Pennings, PS (2005). "Barridos suaves: genética molecular de poblaciones de adaptación a partir de variación genética permanente". Genética . 169 (4): 2335–2352. doi :10.1534/genetics.104.036947. PMC 1449620 . PMID  15716498. 
  19. ^ Gillespie, John (2004). Genética de poblaciones: una guía concisa (2.ª ed.). Johns Hopkins University Press. ISBN 978-0-8018-8008-7.
  20. ^ Miko, I. (2008). "Epistasis: interacción genética y efectos fenotípicos". Nature Education . 1 (1): 197.
  21. ^ Berger, D.; Postma, E. (13 de octubre de 2014). "¿Estimaciones sesgadas de la epistasis de rendimientos decrecientes? Evidencia empírica revisada". Genética . 198 (4): 1417–1420. doi :10.1534/genetics.114.169870. PMC 4256761 . PMID  25313131. 
  22. ^ Kouyos, Roger D.; Silander, Olin K.; Bonhoeffer, Sebastian (junio de 2007). "Epistasis entre mutaciones deletéreas y la evolución de la recombinación". Tendencias en ecología y evolución . 22 (6): 308–315. Bibcode :2007TEcoE..22..308K. doi :10.1016/j.tree.2007.02.014. PMID  17337087.
  23. ^ Crow, JF (5 de agosto de 1997). "La alta tasa de mutación espontánea: ¿es un riesgo para la salud?". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 94 (16): 8380–8386. Bibcode :1997PNAS...94.8380C. doi : 10.1073/pnas.94.16.8380 . PMC 33757 . PMID  9237985. 
  24. ^ Hastings, PJ; Lupski, JR; Rosenberg, SM; Ira, G. (2009). "Mecanismos de cambio en el número de copias de genes". Nature Reviews Genetics . 10 (8): 551–564. doi :10.1038/nrg2593. PMC 2864001 . PMID  19597530. 
  25. ^ M., Long; Betrán, E.; Thornton, K.; Wang, W. (noviembre de 2003). "El origen de nuevos genes: visiones desde los jóvenes y los viejos". Nat. Rev. Genet . 4 (11): 865–75. doi :10.1038/nrg1204. PMID  14634634. S2CID  33999892.
  26. ^ Liu, N.; Okamura, K.; Tyler, DM; Phillips; Chung; Lai (2008). "La evolución y diversificación funcional de los genes de microARN animales". Cell Research . 18 (10): 985–996. doi :10.1038/cr.2008.278. PMC 2712117 . PMID  18711447. 
  27. ^ McLysaght, Aoife; Hurst, Laurence D. (25 de julio de 2016). "Preguntas abiertas en el estudio de genes de novo: qué, cómo y por qué". Nature Reviews Genetics . 17 (9): 567–578. doi :10.1038/nrg.2016.78. PMID  27452112. S2CID  6033249.
  28. ^ Sawyer, SA; Parsch, J.; Zhang, Z.; Hartl, DL (2007). "Prevalencia de selección positiva entre reemplazos de aminoácidos casi neutros en Drosophila". Actas de la Academia Nacional de Ciencias . 104 (16): 6504–6510. Bibcode :2007PNAS..104.6504S. doi : 10.1073/pnas.0701572104 . ISSN  0027-8424. PMC 1871816 . PMID  17409186. 
  29. ^ Crow, James F.; Kimura, Motoo (1970). Introducción a la teoría de la genética de poblaciones (ed. [Reimpresión]). Nueva Jersey: Blackburn Press. ISBN 9781932846126.
  30. ^ Lynch, Michael (agosto de 2010). "Evolución de la tasa de mutación". Tendencias en genética . 26 (8): 345–352. doi :10.1016/j.tig.2010.05.003. PMC 2910838 . PMID  20594608. 
  31. ^ JBS Haldane (1932). Las causas de la evolución . Longmans, Green and Co., Nueva York.
  32. ^ M. Kimura (1980). "Tiempo medio hasta la fijación de un alelo mutante en una población finita bajo presión de mutación continua: estudios mediante métodos analíticos, numéricos y de pseudomuestreo". Proc Natl Acad Sci USA . 77 (1): 522–526. Bibcode :1980PNAS...77..522K. doi : 10.1073/pnas.77.1.522 . PMC 348304 . PMID  16592764. 
  33. ^ Haldane, JBS (1933). "El papel de la mutación recurrente en la evolución". American Naturalist . 67 (708): 5–19. doi :10.1086/280465. JSTOR  2457127. S2CID  84059440.
  34. ^ Protas, Meredith; Conrad, M.; Gross, JB; Tabin, C.; Borowsky, R (2007). "Evolución regresiva en el tetra de cueva mexicano, Astyanax mexicanus". Current Biology . 17 (5): 452–454. Bibcode :2007CBio...17..452P. doi :10.1016/j.cub.2007.01.051. PMC 2570642 . PMID  17306543. 
  35. ^ H. Maughan, J. Masel, CW Birky, Jr. y WL Nicholson (2007). "Los roles de la acumulación y selección de mutaciones en la pérdida de esporulación en poblaciones experimentales de Bacillus subtilis". Genética . 177 (2): 937–48. doi :10.1534/genetics.107.075663. PMC 2034656 . PMID  17720926. {{cite journal}}: CS1 maint: multiple names: authors list (link)
  36. ^ Masel, J. ; King, OD; Maughan, H. (2007). "La pérdida de plasticidad adaptativa durante largos períodos de estasis ambiental". American Naturalist . 169 (1): 38–46. doi :10.1086/510212. PMC 1766558 . PMID  17206583. 
  37. ^ K. Gomez, J. Bertram y J. Masel (2020). "El sesgo de mutación puede moldear la adaptación en grandes poblaciones asexuales que experimentan interferencia clonal". Proc. R. Soc. B . 287 (1937): 20201503. doi :10.1098/rspb.2020.1503. PMC 7661309 . PMID  33081612. 
  38. ^ AV Cano, H. Rozhonova, A. Stoltzfus, DM McCandlish y JL Payne (10 de febrero de 2022). "El sesgo de mutación moldea el espectro de sustituciones adaptativas". Proc Natl Acad Sci USA . 119 (7). Bibcode :2022PNAS..11919720C. doi : 10.1073/pnas.2119720119 . PMC 8851560 . PMID  35145034. {{cite journal}}: CS1 maint: multiple names: authors list (link)
  39. ^ Stoltzfus, A.; Yampolsky, LY (2009). "Escalando el Monte Probable: La mutación como causa de la no aleatoriedad en la evolución". Journal of Heredity . 100 (5): 637–647. doi : 10.1093/jhered/esp048 . PMID  19625453.
  40. ^ ab Masel, J. (2011). "Deriva genética". Current Biology . 21 (20): R837–R838. Código Bibliográfico :2011CBio...21.R837M. doi : 10.1016/j.cub.2011.08.007 . PMID  22032182.
  41. ^ Futuyma, Douglas (1998). Biología evolutiva . Sinauer Associates . p. Glosario. ISBN. 978-0-87893-189-7.
  42. ^ Avers, Charlotte (1989). Proceso y patrón en la evolución . Oxford University Press.
  43. ^ Wahl, LM (2011). "Fijación cuando N y s varían: los enfoques clásicos dan resultados nuevos y elegantes". Genética . 188 (4): 783–785. doi :10.1534/genetics.111.131748. PMC 3176088 . PMID  21828279. 
  44. ^ Barton, Nicholas H.; Briggs, Derek EG; Eisen, Jonathan A.; Goldstein, David B.; Patel, Nipam H. (2007). Evolución . Cold Spring Harbor Laboratory Press. pág. 417. ISBN 978-0-87969-684-9.
  45. ^ Futuyma, Douglas (1998). Biología evolutiva . Sinauer Associates . pág. 320. ISBN. 978-0-87893-189-7.
  46. ^ Gillespie, JH (2000). "Deriva genética en una población infinita: el modelo de pseudoautostop". Genética . 155 (2): 909–919. doi :10.1093/genetics/155.2.909. PMC 1461093 . PMID  10835409. 
  47. ^ Provine, William B. La falacia de la "deriva genética aleatoria" . CreateSpace.
  48. ^ Neher, Richard A.; Shraiman, Boris I. (agosto de 2011). "Genetic Draft and Quasi-Neutrality in Large Facultatively Sexually Populations" (Proyecto genético y cuasi-neutralidad en grandes poblaciones facultativamente sexuales). Genética . 188 (4): 975–996. arXiv : 1108.1635 . doi :10.1534/genetics.111.128876. ISSN  0016-6731. PMC 3176096 . PMID  21625002. 
  49. ^ Buston, PM; Pilkington, JG; et al. (2007). "¿Los grupos de peces payaso están compuestos por parientes cercanos? Un análisis de la variación del ADN de microsatélites en Amphiprion percula ". Ecología molecular . 12 (3): 733–742. doi :10.1046/j.1365-294X.2003.01762.x. PMID  12675828. S2CID  35546810.
  50. ^ Repaci, V.; Stow, AJ; Briscoe, DA (2007). "Estructura genética a escala fina, cofundación y apareamiento múltiple en la abeja alodapina australiana ( Ramphocinclus brachyurus )". Revista de Zoología . 270 (4): 687–691. doi :10.1111/j.1469-7998.2006.00191.x.
  51. ^ ab Su, H.; Qu, L.-J.; He, K.; Zhang, Z.; Wang, J; Chen, Z.; Gu, H. (2003). "La Gran Muralla China: ¿una barrera física para el flujo genético?". Heredity . 90 (3): 212–219. doi :10.1038/sj.hdy.6800237. ISSN  0018-067X. PMID  12634804. S2CID  13367320.
  52. ^ Gravel, S. (2012). "Modelos de genética poblacional de ascendencia local". Genética . 1202 (2): 607–619. arXiv : 1202.4811 . Código Bibliográfico :2012arXiv1202.4811G. doi :10.1534/genetics.112.139808. PMC 3374321 . PMID  22491189. 
  53. ^ Morjan, C.; Rieseberg, L. (2004). "Cómo evolucionan colectivamente las especies: implicaciones del flujo genético y la selección para la propagación de alelos ventajosos". Ecología molecular . 13 (6): 1341–56. Bibcode :2004MolEc..13.1341M. doi :10.1111/j.1365-294X.2004.02164.x. PMC 2600545 . PMID  15140081. 
  54. ^ Bolnick, Daniel I.; Nosil, Patrik (septiembre de 2007). "Selección natural en poblaciones sujetas a una carga migratoria". Evolución . 61 (9): 2229–2243. doi : 10.1111/j.1558-5646.2007.00179.x . PMID  17767592. S2CID  25685919.
  55. ^ Boucher, Yan; Douady, Christophe J.; Papke, R. Thane; Walsh, David A.; Boudreau, Mary Ellen R.; Nesbø, Camilla L.; Case, Rebecca J.; Doolittle, W. Ford (2003). "Transferencia lateral de genes y los orígenes de los grupos procariotas". Revisión anual de genética . 37 (1): 283–328. doi :10.1146/annurev.genet.37.050503.084247. ISSN  0066-4197. PMID  14616063.
  56. ^ Walsh, T. (2006). "Evolución genética combinatoria de la multirresistencia". Current Opinion in Microbiology . 9 (5): 476–82. doi :10.1016/j.mib.2006.08.009. PMID  16942901.
  57. ^ Kondo, N.; Nikoh, N.; Ijichi, N.; Shimada, M.; Fukatsu, T. (2002). "Fragmento del genoma del endosimbionte de Wolbachia transferido al cromosoma X del insecto huésped". Actas de la Academia Nacional de Ciencias . 99 (22): 14280–14285. Bibcode :2002PNAS...9914280K. doi : 10.1073/pnas.222228199 . ISSN  0027-8424. PMC 137875 . PMID  12386340. 
  58. ^ Sprague, G. (1991). "Intercambio genético entre reinos". Current Opinion in Genetics & Development . 1 (4): 530–533. doi :10.1016/S0959-437X(05)80203-5. PMID  1822285.
  59. ^ Gladyshev, EA; Meselson, M.; Arkhipova, IR (2008). "Transferencia masiva horizontal de genes en rotíferos bdelloideos". Science . 320 (5880): 1210–1213. Bibcode :2008Sci...320.1210G. doi :10.1126/science.1156407. ISSN  0036-8075. PMID  18511688. S2CID  11862013.
  60. ^ Baldo, A.; McClure, M. (1 de septiembre de 1999). "Evolución y transferencia horizontal de genes codificantes de dUTPasa en virus y sus hospedadores". Journal of Virology . 73 (9): 7710–7721. doi :10.1128/JVI.73.9.7710-7721.1999. PMC 104298 . PMID  10438861. 
  61. ^ Poole, A.; Penny, D. (2007). "Evaluación de hipótesis sobre el origen de los eucariotas". BioEssays . 29 (1): 74–84. doi :10.1002/bies.20516. PMID  17187354.
  62. ^ Weissman, DB; Hallatschek, O. (15 de enero de 2014). "La tasa de adaptación en grandes poblaciones sexuales con cromosomas lineales". Genética . 196 (4): 1167–1183. doi :10.1534/genetics.113.160705. PMC 3982688 . PMID  24429280. 
  63. ^ Weissman, Daniel B.; Barton, Nicholas H.; McVean, Gil (7 de junio de 2012). "Límites a la tasa de sustitución adaptativa en poblaciones sexuales". PLOS Genetics . 8 (6): e1002740. doi : 10.1371/journal.pgen.1002740 . PMC 3369949 . PMID  22685419. 
  64. ^ Neher, RA; Shraiman, BI; Fisher, DS (30 de noviembre de 2009). "Tasa de adaptación en grandes poblaciones sexuales". Genética . 184 (2): 467–481. arXiv : 1108.3464 . doi :10.1534/genetics.109.109009. PMC 2828726 . PMID  19948891. 
  65. ^ Desai, Michael M.; Fisher, Daniel S. (2007). "Balance de selección de mutaciones beneficiosas y el efecto del ligamiento en la selección positiva". Genética . 176 (3): 1759–1798. doi :10.1534/genetics.106.067678. PMC 1931526 . PMID  17483432. 
  66. ^ Lewontin, RC (1973). La base genética del cambio evolutivo ([4.ª edición]). Nueva York: Columbia University Press. ISBN 978-0231033923.
  67. ^ ab Ellegren, Hans; Galtier, Nicolas (6 de junio de 2016). "Determinantes de la diversidad genética". Nature Reviews Genetics . 17 (7): 422–433. doi :10.1038/nrg.2016.58. PMID  27265362. S2CID  23531428.
  68. ^ Corbett-Detig, Russell B.; Hartl, Daniel L.; Sackton, Timothy B.; Barton, Nick H. (10 de abril de 2015). "La selección natural restringe la diversidad neutral en una amplia gama de especies". PLOS Biology . 13 (4): e1002112. doi : 10.1371/journal.pbio.1002112 . PMC 4393120 . PMID  25859758. 
  69. ^ Sung, W.; Ackerman, MS; Miller, SF; Doak, TG; Lynch, M. (17 de octubre de 2012). "Hipótesis de la barrera de deriva y evolución de la tasa de mutación" (PDF) . Actas de la Academia Nacional de Ciencias . 109 (45): 18488–18492. Bibcode :2012PNAS..10918488S. doi : 10.1073/pnas.1216223109 . PMC 3494944 . PMID  23077252. 
  70. ^ Charlesworth, J. Eyre-Walker (2008). "La prueba McDonald–Kreitman y mutaciones ligeramente perjudiciales". Biología molecular y evolución . 25 (6): 1007–1015. doi : 10.1093/molbev/msn005 . PMID  18195052.
  71. ^ Eyre-Walker, A. (2006). "La tasa genómica de la evolución adaptativa" (PDF) . Tendencias en ecología y evolución . 21 (10): 569–575. Bibcode :2006TEcoE..21..569E. doi :10.1016/j.tree.2006.06.015. PMID  16820244.
  72. ^ Smith, NGC; Eyre-Walker, A. (2002). "Evolución adaptativa de proteínas en Drosophila". Nature . 415 (6875): 1022–1024. Bibcode :2002Natur.415.1022S. doi :10.1038/4151022a. PMID  11875568. S2CID  4426258.
  73. ^ Hahn, MW (2008). "Hacia una teoría de selección de la evolución molecular". Evolución . 62 (2): 255–265. doi : 10.1111/j.1558-5646.2007.00308.x . PMID  18302709. S2CID  5986211.
  74. ^ Pritchard, JK; Stephens, M.; Donnelly, P. (junio de 2000). "Inferencia de la estructura de la población utilizando datos de genotipos multilocus". Genética . 155 (2): 945–959. doi :10.1093/genetics/155.2.945. ISSN  0016-6731. PMC 1461096 . PMID  10835412. 
  75. ^ Verity, Robert; Nichols, Richard A. (agosto de 2016). "Estimación del número de subpoblaciones (K) en poblaciones estructuradas". Genética . 203 (4): 1827–1839. doi :10.1534/genetics.115.180992. ISSN  0016-6731. PMC 4981280 . PMID  27317680. 
  76. ^ Manlik, Oliver; Chabanne, Delphine; Daniel, Claire; Bejder, Lars; Allen, Simon J.; Sherwin, William B. (13 de noviembre de 2018). "La demografía y la genética sugieren una inversión de la dinámica de origen-destino de los delfines, con implicaciones para la conservación". Marine Mammal Science . 35 (3): 732–759. doi :10.1111/mms.12555. S2CID  92108810.
  77. ^ Gutenkunst, Ryan N.; Hernandez, Ryan D.; Williamson, Scott H.; Bustamante, Carlos D.; McVean, Gil (23 de octubre de 2009). "Inferir la historia demográfica conjunta de múltiples poblaciones a partir de datos de frecuencia de SNP multidimensionales". PLOS Genetics . 5 (10): e1000695. arXiv : 0909.0925 . doi : 10.1371/journal.pgen.1000695 . PMC 2760211 . PMID  19851460. 
  78. ^ Sniegowski, P. (2000). "La evolución de las tasas de mutación: separando las causas de las consecuencias". BioEssays . 22 (12). Gerrish P.; Johnson T;. Shaver A.: 1057–1066. doi :10.1002/1521-1878(200012)22:12<1057::AID-BIES3>3.0.CO;2-W. PMID  11084621. S2CID  36771934.
  79. ^ Lynch, Michael; Conery, John S. (2003). "Los orígenes de la complejidad del genoma". Science . 302 (5649): 1401–1404. Bibcode :2003Sci...302.1401L. CiteSeerX 10.1.1.135.974 . doi :10.1126/science.1089370. PMID  14631042. S2CID  11246091. 
  80. ^ Rajon, E.; Masel, J. (3 de enero de 2011). "Evolución de las tasas de error molecular y las consecuencias para la capacidad evolutiva". Actas de la Academia Nacional de Ciencias . 108 (3): 1082–1087. Bibcode :2011PNAS..108.1082R. doi : 10.1073/pnas.1012918108 . PMC 3024668 . PMID  21199946. 

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Genética de poblaciones .