
En matemáticas , la geometría hiperbólica (también llamada geometría lobachevskiana o geometría bolyai - lobachevskiana ) es una geometría no euclidiana . El postulado de las paralelas de la geometría euclidiana se sustituye por:
(Compare lo anterior con el axioma de Playfair , la versión moderna del postulado de las paralelas de Euclides ).
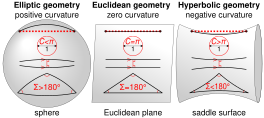
El plano hiperbólico es un plano en el que cada punto es un punto de silla . La geometría del plano hiperbólico también es la geometría de las superficies pseudoesféricas , superficies con una curvatura gaussiana negativa constante . Las superficies de silla tienen una curvatura gaussiana negativa al menos en algunas regiones, donde se parecen localmente al plano hiperbólico.
El modelo hiperboloide de la geometría hiperbólica proporciona una representación de los acontecimientos que se producen una unidad temporal en el futuro en el espacio de Minkowski , la base de la relatividad especial . Cada uno de estos acontecimientos corresponde a una rapidez en alguna dirección.
Cuando los geómetras se dieron cuenta por primera vez de que estaban trabajando con algo distinto a la geometría euclidiana estándar, describieron su geometría con muchos nombres diferentes; Felix Klein finalmente le dio al tema el nombre de geometría hiperbólica para incluirla en la secuencia ahora raramente utilizada de geometría elíptica ( geometría esférica ), geometría parabólica ( geometría euclidiana ) y geometría hiperbólica. En la ex Unión Soviética , se la llama comúnmente geometría lobachevskiana, llamada así por uno de sus descubridores, el geómetra ruso Nikolai Lobachevsky .
La geometría hiperbólica está más relacionada con la geometría euclidiana de lo que parece: la única diferencia axiomática es el postulado de las paralelas . Cuando se elimina el postulado de las paralelas de la geometría euclidiana, la geometría resultante es la geometría absoluta . Hay dos tipos de geometría absoluta, la euclidiana y la hiperbólica. Todos los teoremas de la geometría absoluta, incluidas las primeras 28 proposiciones del libro uno de los Elementos de Euclides , son válidos en la geometría euclidiana e hiperbólica. Las proposiciones 27 y 28 del Libro Uno de los Elementos de Euclides prueban la existencia de líneas paralelas/no intersecantes.
Esta diferencia también tiene muchas consecuencias: los conceptos que son equivalentes en la geometría euclidiana no lo son en la geometría hiperbólica; es necesario introducir nuevos conceptos. Además, debido al ángulo de paralelismo , la geometría hiperbólica tiene una escala absoluta , una relación entre las medidas de distancia y ángulo.
Las líneas simples en la geometría hiperbólica tienen exactamente las mismas propiedades que las líneas rectas simples en la geometría euclidiana. Por ejemplo, dos puntos definen de manera única una línea y los segmentos de línea pueden extenderse infinitamente.
Dos líneas que se intersecan tienen las mismas propiedades que dos líneas que se intersecan en la geometría euclidiana. Por ejemplo, dos líneas distintas pueden intersecar en un único punto, las líneas que se intersecan forman ángulos opuestos iguales y los ángulos adyacentes de las líneas que se intersecan son suplementarios .
Cuando se introduce una tercera línea, pueden existir propiedades de las líneas que se intersecan que difieran de las líneas que se intersecan en la geometría euclidiana. Por ejemplo, dadas dos líneas que se intersecan, hay infinitas líneas que no intersecan ninguna de las líneas dadas.
Todas estas propiedades son independientes del modelo utilizado, incluso si las líneas pueden parecer radicalmente diferentes.

Las líneas que no se intersecan en la geometría hiperbólica también tienen propiedades que difieren de las líneas que no se intersecan en la geometría euclidiana :
Esto implica que a través de P hay un número infinito de líneas coplanares que no intersecan a R.
Estas líneas que no se intersecan se dividen en dos clases:
Algunos geómetras simplemente usan la frase " líneas paralelas " para significar " líneas paralelas limitantes ", mientras que líneas ultraparalelas significan simplemente líneas que no se intersecan .
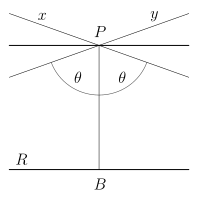
Estos paralelos límite forman un ángulo θ con PB ; este ángulo depende únicamente de la curvatura gaussiana del plano y de la distancia PB y se llama ángulo de paralelismo .
Para las líneas ultraparalelas, el teorema ultraparalelo establece que hay una única línea en el plano hiperbólico que es perpendicular a cada par de líneas ultraparalelas.
En geometría hiperbólica, la circunferencia de un círculo de radio r es mayor que .
Sea , donde es la curvatura gaussiana del plano. En geometría hiperbólica, es negativo, por lo que la raíz cuadrada es de un número positivo.
Entonces la circunferencia de un círculo de radio r es igual a:
Y el área del disco encerrado es:
Por lo tanto, en geometría hiperbólica, la relación entre la circunferencia de un círculo y su radio es siempre estrictamente mayor que , aunque puede hacerse arbitrariamente cercana seleccionando un círculo suficientemente pequeño.
Si la curvatura gaussiana del plano es −1 entonces la curvatura geodésica de un círculo de radio r es: [1]

En la geometría hiperbólica no existe una línea cuyos puntos sean todos equidistantes de otra línea, sino que los puntos que están todos a la misma distancia de una línea dada se encuentran en una curva llamada hiperciclo .
Otra curva especial es el horociclo , cuyos radios normales ( líneas perpendiculares ) son todos paralelos entre sí (todos convergen asintóticamente en una dirección al mismo punto ideal , el centro del horociclo).
Por cada par de puntos hay dos horociclos, cuyos centros son los puntos ideales de la mediatriz del segmento comprendido entre ellos.
Dados tres puntos distintos, todos ellos se encuentran en una línea, un hiperciclo, un horociclo o un círculo.
La longitud de un segmento de línea es la longitud más corta entre dos puntos.
La longitud del arco de un hiperciclo que conecta dos puntos es más larga que la del segmento de línea y más corta que la del arcohorociclo que conecta los mismos dos puntos.
Las longitudes de los arcos de ambos hiperciclos que unen dos puntos son iguales, y son más largas que la longitud de arco de cualquier hiperciclo que conecte los puntos y más cortas que el arco de cualquier círculo que conecte los dos puntos.
Si la curvatura gaussiana del plano es −1, entonces la curvatura geodésica de un horociclo es 1 y la de un hiperciclo está entre 0 y 1. [1]
A diferencia de los triángulos euclidianos, donde los ángulos siempre suman π radianes (180°, un ángulo llano ), en el espacio hiperbólico la suma de los ángulos de un triángulo es siempre estrictamente menor que π radianes (180°). La diferencia se llama defecto . Generalmente, el defecto de un polígono hiperbólico convexo con lados es la suma de sus ángulos restada de .
El área de un triángulo hiperbólico está dada por su defecto en radianes multiplicado por R 2 , lo que también es cierto para todos los polígonos hiperbólicos convexos. [2] Por lo tanto, todos los triángulos hiperbólicos tienen un área menor o igual a R 2 π. El área de un triángulo ideal hiperbólico en el que los tres ángulos son 0° es igual a este máximo.
Al igual que en la geometría euclidiana , cada triángulo hiperbólico tiene un círculo inscrito . En el espacio hiperbólico, si sus tres vértices se encuentran en un horociclo o hiperciclo , entonces el triángulo no tiene un círculo circunscrito .
Al igual que en la geometría esférica y elíptica , en la geometría hiperbólica, si dos triángulos son semejantes, deben ser congruentes.

Los polígonos especiales en geometría hiperbólica son los polígonos regulares uniformes apeirógonos y pseudogonos con un número infinito de lados.
En la geometría euclidiana , la única forma de construir un polígono de este tipo es hacer que las longitudes de los lados tiendan a cero y el apeirógono sea indistinguible de un círculo, o hacer que los ángulos interiores tiendan a 180° y el apeirógono se aproxime a una línea recta.
Sin embargo, en geometría hiperbólica, un apeirógono o pseudogono regular tiene lados de cualquier longitud (es decir, sigue siendo un polígono con lados visibles).
Las bisectrices de los lados y de los ángulos serán, según la longitud de los lados y el ángulo entre los lados, paralelas limitantes o divergentes. Si las bisectrices son paralelas limitantes, entonces es un apeirógono y puede estar inscrito y circunscrito por horociclos concéntricos .
Si las bisectrices divergen paralelamente entonces es un pseudogono y puede inscribirse y circunscribirse mediante hiperciclos (todos los vértices están a la misma distancia de una recta, el eje, también el punto medio de los segmentos laterales son todos equidistantes al mismo eje).

Al igual que el plano euclidiano, también es posible teselar el plano hiperbólico con polígonos regulares como caras .
Hay un número infinito de teselados uniformes basados en los triángulos de Schwarz ( p q r ) donde 1/ p + 1/ q + 1/ r < 1, donde p , q , r son cada uno órdenes de simetría de reflexión en tres puntos del triángulo de dominio fundamental , el grupo de simetría es un grupo de triángulos hiperbólicos . También hay infinitos teselados uniformes que no se pueden generar a partir de triángulos de Schwarz, algunos, por ejemplo, requieren cuadriláteros como dominios fundamentales. [3]
Aunque la geometría hiperbólica se aplica a cualquier superficie con una curvatura gaussiana negativa constante , es habitual suponer una escala en la que la curvatura K es −1.
Esto hace que algunas fórmulas se simplifiquen. Algunos ejemplos son:
En comparación con la geometría euclidiana, la geometría hiperbólica presenta muchas dificultades para un sistema de coordenadas: la suma de los ángulos de un cuadrilátero es siempre menor que 360°; no hay líneas equidistantes, por lo que un rectángulo adecuado debería estar encerrado por dos líneas y dos hiperciclos; transportar en paralelo un segmento de línea alrededor de un cuadrilátero hace que gire cuando regresa al origen, etc.
Sin embargo, existen diferentes sistemas de coordenadas para la geometría del plano hiperbólico. Todos se basan en la elección de un punto (el origen) en una línea dirigida elegida (el eje x ) y, a partir de ahí, existen muchas opciones.
Las coordenadas x e y de Lobachevsky se obtienen colocando una perpendicular sobre el eje x . x será la etiqueta del pie de la perpendicular. y será la distancia a lo largo de la perpendicular del punto dado desde su pie (positiva en un lado y negativa en el otro).
Otro sistema de coordenadas mide la distancia desde el punto hasta el horociclo a través del origen centrado alrededor y la longitud a lo largo de este horociclo. [5]
Otros sistemas de coordenadas utilizan el modelo de Klein o el modelo de disco de Poincaré descritos a continuación y toman las coordenadas euclidianas como hiperbólicas.
Un sistema de coordenadas cartesiano [ cita requerida ] ( x, y ) en el plano hiperbólico orientado se construye de la siguiente manera. Elija una línea en el plano hiperbólico junto con una orientación y un origen o en esta línea. Luego:
La distancia entre dos puntos representados por ( x_i, y_i ), i=1,2 en este sistema de coordenadas es [ cita requerida ]
Esta fórmula se puede derivar de las fórmulas sobre triángulos hiperbólicos .
El campo tensor métrico correspondiente es: .
En este sistema de coordenadas, las líneas rectas toman una de estas formas (( x , y ) es un punto en la línea; x 0 , y 0 , A y α son parámetros):
ultraparalelo al eje x
asintóticamente paralela en el lado negativo
asintóticamente paralelo en el lado positivo
intersecándose perpendicularmente
intersecándose en un ángulo α
En general, estas ecuaciones solo se cumplen en un dominio acotado (de valores x ). En el borde de ese dominio, el valor de y aumenta hasta ±infinito.
Desde la publicación de los Elementos de Euclides alrededor del año 300 a. C., muchos geómetras intentaron demostrar el postulado de las paralelas . Algunos intentaron demostrarlo asumiendo su negación y tratando de derivar una contradicción . Entre ellos, los más destacados fueron Proclo , Ibn al-Haytham (Alhacen), Omar Khayyám , [6] Nasīr al-Dīn al-Tūsī , Witelo , Gersonides , Alfonso y, más tarde, Giovanni Gerolamo Saccheri , John Wallis , Johann Heinrich Lambert y Legendre . [7] Sus intentos estaban condenados al fracaso (como ahora sabemos, el postulado de las paralelas no se puede demostrar a partir de los otros postulados), pero sus esfuerzos condujeron al descubrimiento de la geometría hiperbólica.
Los teoremas de Alhacen, Khayyam y al-Tūsī sobre cuadriláteros , incluidos el cuadrilátero de Ibn al-Haytham-Lambert y el cuadrilátero de Khayyam-Saccheri , fueron los primeros teoremas sobre geometría hiperbólica. Sus trabajos sobre geometría hiperbólica tuvieron una influencia considerable en su desarrollo entre los geómetras europeos posteriores, incluidos Witelo, Gersonides, Alfonso, John Wallis y Saccheri. [8]
En el siglo XVIII, Johann Heinrich Lambert introdujo las funciones hiperbólicas [9] y calculó el área de un triángulo hiperbólico . [10]
En el siglo XIX, la geometría hiperbólica fue explorada extensamente por Nikolai Lobachevsky , János Bolyai , Carl Friedrich Gauss y Franz Taurinus . A diferencia de sus predecesores, que solo querían eliminar el postulado de las paralelas de los axiomas de la geometría euclidiana, estos autores se dieron cuenta de que habían descubierto una nueva geometría. [11] [12]
En una carta de 1824 a Franz Taurinus, Gauss escribió que la había construido, pero no publicó su trabajo. Gauss la llamó « geometría no euclidiana » [13], lo que provocó que varios autores modernos siguieran considerando que «geometría no euclidiana» y «geometría hiperbólica» eran sinónimos. Taurinus publicó resultados sobre trigonometría hiperbólica en 1826, argumentó que la geometría hiperbólica es autoconsistente, pero todavía creía en el papel especial de la geometría euclidiana. El sistema completo de geometría hiperbólica fue publicado por Lobachevsky en 1829/1830, mientras que Bolyai lo descubrió de forma independiente y lo publicó en 1832.
En 1868, Eugenio Beltrami proporcionó modelos de geometría hiperbólica y los utilizó para demostrar que la geometría hiperbólica era consistente si y sólo si la geometría euclidiana lo era.
El término "geometría hiperbólica" fue introducido por Felix Klein en 1871. [14] Klein siguió una iniciativa de Arthur Cayley de utilizar las transformaciones de la geometría proyectiva para producir isometrías . La idea utilizaba una sección cónica o cuadrática para definir una región, y utilizaba la razón cruzada para definir una métrica . Las transformaciones proyectivas que dejan estable la sección cónica o cuadrática son las isometrías. "Klein demostró que si el absoluto de Cayley es una curva real, entonces la parte del plano proyectivo en su interior es isométrica al plano hiperbólico..." [15]
El descubrimiento de la geometría hiperbólica tuvo importantes consecuencias filosóficas . Antes de su descubrimiento, muchos filósofos (como Hobbes y Spinoza ) consideraban el rigor filosófico en términos del "método geométrico", haciendo referencia al método de razonamiento utilizado en los Elementos de Euclides .
Kant, en su Crítica de la razón pura, concluyó que el espacio (en la geometría euclidiana ) y el tiempo no son descubiertos por los humanos como características objetivas del mundo, sino que son parte de un marco sistemático inevitable para organizar nuestras experiencias. [16]
Se dice que Gauss no publicó nada sobre geometría hiperbólica por miedo al "alboroto de los beocios " (estereotipados como tontos por los antiguos atenienses [17] ), que arruinaría su condición de princeps mathematicorum (del latín, "el príncipe de los matemáticos"). [18] El "alboroto de los beocios" vino y se fue, y dio un impulso a grandes mejoras en el rigor matemático , la filosofía analítica y la lógica . La geometría hiperbólica finalmente demostró ser consistente y, por lo tanto, es otra geometría válida.
Como la geometría euclidiana, hiperbólica y elíptica son todas consistentes, surge la pregunta: ¿cuál es la geometría real del espacio y, si es hiperbólica o elíptica, cuál es su curvatura?
Lobachevsky ya había intentado medir la curvatura del universo midiendo la paralaje de Sirio y tratando a Sirio como el punto ideal de un ángulo de paralelismo . Se dio cuenta de que sus mediciones no eran lo suficientemente precisas como para dar una respuesta definitiva, pero llegó a la conclusión de que si la geometría del universo es hiperbólica, entonces la longitud absoluta es al menos un millón de veces el diámetro de la órbita de la Tierra (2 000 000 UA , 10 parsec ). [19] Algunos sostienen que sus mediciones tenían fallas metodológicas. [20]
Henri Poincaré , con su experimento mental del mundo esférico , llegó a la conclusión de que la experiencia cotidiana no descarta necesariamente otras geometrías.
La conjetura de geometrización ofrece una lista completa de ocho posibilidades para la geometría fundamental de nuestro espacio. El problema para determinar cuál de ellas es aplicable es que, para llegar a una respuesta definitiva, necesitamos poder observar formas extremadamente grandes, mucho más grandes que cualquier cosa que haya en la Tierra o tal vez incluso en nuestra galaxia. [21]
La relatividad especial coloca al espacio y al tiempo en pie de igualdad, de modo que se considera la geometría de un espacio-tiempo unificado en lugar de considerar el espacio y el tiempo por separado. [22] [23] La geometría de Minkowski reemplaza a la geometría galileana (que es el espacio euclidiano tridimensional con el tiempo de la relatividad galileana ). [24]
En relatividad, en lugar de la geometría euclidiana, elíptica e hiperbólica, las geometrías apropiadas a considerar son el espacio de Minkowski , el espacio de De Sitter y el anti-espacio de De Sitter , [25] [26] correspondientes a curvatura cero, positiva y negativa respectivamente.
La geometría hiperbólica entra en la relatividad especial a través de la rapidez , que sustituye a la velocidad , y se expresa mediante un ángulo hiperbólico . El estudio de esta geometría de la velocidad se ha denominado geometría cinemática . El espacio de velocidades relativistas tiene una geometría hiperbólica tridimensional, donde la función de distancia se determina a partir de las velocidades relativas de los puntos "cercanos" (velocidades). [27]


Existen varias pseudoesferas en el espacio euclidiano que tienen un área finita de curvatura gaussiana negativa constante.
Según el teorema de Hilbert , no se puede sumergir isométricamente un plano hiperbólico completo (una superficie regular completa de curvatura gaussiana negativa constante ) en un espacio euclidiano tridimensional.
Existen otros modelos útiles de geometría hiperbólica en el espacio euclidiano, en los que no se conserva la métrica. Un modelo de papel particularmente conocido basado en la pseudoesfera se debe a William Thurston .
El arte del crochet se ha utilizado para demostrar planos hiperbólicos, siendo la primera demostración de este tipo realizada por Daina Taimiņa . [28]
En 2000, Keith Henderson demostró un modelo de papel fácil de hacer, denominado " balón de fútbol hiperbólico " (más precisamente, un mosaico triangular truncado de orden 7 ). [29] [30]
Jeff Weeks ha puesto a disposición instrucciones sobre cómo hacer una colcha hiperbólica, diseñada por Helaman Ferguson [ 31] . [32]
Varias pseudoesferas (superficies con curvatura gaussiana negativa constante) pueden incorporarse al espacio tridimensional según la métrica euclidiana estándar, y así convertirse en modelos tangibles. De ellas, la tractoide (o pseudoesfera) es la más conocida; utilizar la tractoide como modelo del plano hiperbólico es análogo a utilizar un cono o un cilindro como modelo del plano euclidiano. Sin embargo, el plano hiperbólico entero no puede incorporarse al espacio euclidiano de esta manera, y existen otros modelos más convenientes para explorar de forma abstracta la geometría hiperbólica.
Existen cuatro modelos que se utilizan comúnmente para la geometría hiperbólica: el modelo de Klein , el modelo del disco de Poincaré , el modelo del semiplano de Poincaré y el modelo de Lorentz o hiperboloide . Estos modelos definen un plano hiperbólico que satisface los axiomas de una geometría hiperbólica. A pesar de sus nombres, los tres primeros mencionados anteriormente fueron introducidos como modelos del espacio hiperbólico por Beltrami , no por Poincaré o Klein . Todos estos modelos son extensibles a más dimensiones.
El modelo de Beltrami-Klein , también conocido como modelo de disco proyectivo, modelo de disco de Klein y modelo de Klein , lleva el nombre de Eugenio Beltrami y Felix Klein .
Para las dos dimensiones, este modelo utiliza el interior del círculo unitario para el plano hiperbólico completo , y las cuerdas de este círculo son las líneas hiperbólicas.
Para dimensiones superiores, este modelo utiliza el interior de la bola unitaria , y las cuerdas de esta n -bola son las líneas hiperbólicas.
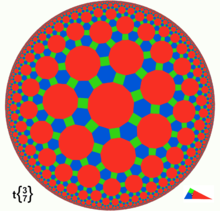
El modelo de disco de Poincaré , también conocido como modelo de disco conforme, también emplea el interior del círculo unitario , pero las líneas están representadas por arcos de círculos que son ortogonales al círculo límite, más los diámetros del círculo límite.
El modelo de semiplano de Poincaré considera que la mitad del plano euclidiano, delimitado por una línea B del plano, es un modelo del plano hiperbólico. La línea B no está incluida en el modelo.
El plano euclidiano puede tomarse como un plano con el sistema de coordenadas cartesianas y el eje x se toma como la línea B y el semiplano es la mitad superior ( y > 0 ) de este plano.
El modelo hiperboloide o modelo de Lorentz emplea un hiperboloide de revolución bidimensional (de dos láminas, pero utilizando una) inserto en un espacio de Minkowski tridimensional . Este modelo se atribuye generalmente a Poincaré, pero Reynolds [33] dice que Wilhelm Killing utilizó este modelo en 1885.
El modelo hemisférico no suele utilizarse como modelo por sí solo, pero funciona como una herramienta útil para visualizar transformaciones entre los otros modelos.
El modelo de hemisferio utiliza la mitad superior de la esfera unitaria :
Las líneas hiperbólicas son semicírculos ortogonales al límite del hemisferio.
El modelo del hemisferio es parte de una esfera de Riemann , y diferentes proyecciones dan diferentes modelos del plano hiperbólico:
En 1966, David Gans propuso un modelo hiperboloide aplanado en la revista American Mathematical Monthly . [34] Se trata de una proyección ortográfica del modelo hiperboloide sobre el plano xy. Este modelo no se utiliza tan ampliamente como otros modelos, pero sin embargo es bastante útil para comprender la geometría hiperbólica.
El modelo de banda emplea una porción del plano euclidiano entre dos líneas paralelas. [36] La distancia se conserva a lo largo de una línea que pasa por el medio de la banda. Suponiendo que la banda está dada por , la métrica está dada por .

Todos los modelos describen esencialmente la misma estructura. La diferencia entre ellos es que representan diferentes gráficos de coordenadas establecidos en el mismo espacio métrico , es decir, el plano hiperbólico. La característica característica del propio plano hiperbólico es que tiene una curvatura gaussiana negativa constante , que es indiferente al gráfico de coordenadas utilizado. Las geodésicas son igualmente invariantes: es decir, las geodésicas se asignan a geodésicas bajo transformación de coordenadas. La geometría hiperbólica se introduce generalmente en términos de las geodésicas y sus intersecciones en el plano hiperbólico. [37]
Una vez que elegimos un gráfico de coordenadas (uno de los "modelos"), siempre podemos incrustarlo en un espacio euclidiano de la misma dimensión, pero la incrustación claramente no es isométrica (ya que la curvatura del espacio euclidiano es 0). El espacio hiperbólico puede representarse mediante una infinidad de gráficos diferentes; pero las incrustaciones en el espacio euclidiano debidas a estos cuatro gráficos específicos muestran algunas características interesantes.
Dado que los cuatro modelos describen el mismo espacio métrico, cada uno puede transformarse en el otro.
Véase, por ejemplo:
Toda isometría ( transformación o movimiento ) del plano hiperbólico respecto de sí mismo puede realizarse como la composición de, como máximo, tres reflexiones . En un espacio hiperbólico de n dimensiones, pueden requerirse hasta n +1 reflexiones. (Esto también es válido para las geometrías esférica y euclidiana, pero la clasificación que se indica a continuación es diferente).
Todas las isometrías del plano hiperbólico se pueden clasificar en estas clases:
Los famosos grabados de MC Escher Círculo límite III y Círculo límite IV ilustran bastante bien el modelo de disco conforme ( modelo de disco de Poincaré ). Las líneas blancas en III no son exactamente geodésicas (son hiperciclos ), pero están cerca de serlo. También es posible ver con bastante claridad la curvatura negativa del plano hiperbólico, a través de su efecto sobre la suma de ángulos en triángulos y cuadrados.
Por ejemplo, en Circle Limit III cada vértice pertenece a tres triángulos y tres cuadrados. En el plano euclidiano, sus ángulos sumarían 450°; es decir, un círculo y un cuarto. De esto, vemos que la suma de los ángulos de un triángulo en el plano hiperbólico debe ser menor que 180°. Otra propiedad visible es el crecimiento exponencial . En Circle Limit III , por ejemplo, se puede ver que el número de peces dentro de una distancia de n desde el centro aumenta exponencialmente. Los peces tienen un área hiperbólica igual, por lo que el área de una pelota de radio n debe aumentar exponencialmente en n .
El arte del crochet se ha utilizado para demostrar planos hiperbólicos (en la foto de arriba), siendo el primero realizado por Daina Taimiņa , [28] cuyo libro Crocheting Adventures with Hyperbolic Planes ganó el premio Bookseller/Diagram Prize 2009 al título más extraño del año . [38]
HyperRogue es un juego roguelike ambientado en varios mosaicos del plano hiperbólico .
La geometría hiperbólica no se limita a dos dimensiones; existe una geometría hiperbólica para cada número mayor de dimensiones.
El espacio hiperbólico de dimensión n es un caso especial de un espacio simétrico riemanniano de tipo no compacto, ya que es isomorfo al cociente
El grupo ortogonal O(1, n ) actúa mediante transformaciones que preservan la norma en el espacio de Minkowski R 1, n , y actúa transitivamente en el hiperboloide de dos hojas de vectores de norma 1. Las líneas temporales (es decir, aquellas con tangentes de norma positiva) que pasan por el origen pasan por puntos antípodas en el hiperboloide, por lo que el espacio de tales líneas produce un modelo de n -espacio hiperbólico. El estabilizador de cualquier línea particular es isomorfo al producto de los grupos ortogonales O( n ) y O(1), donde O( n ) actúa en el espacio tangente de un punto en el hiperboloide, y O(1) refleja la línea que pasa por el origen. Muchos de los conceptos elementales en geometría hiperbólica se pueden describir en términos algebraicos lineales : las trayectorias geodésicas se describen por intersecciones con planos que pasan por el origen, los ángulos diedros entre hiperplanos se pueden describir por productos internos de vectores normales, y a los grupos de reflexión hiperbólica se les pueden dar realizaciones matriciales explícitas.
En pequeñas dimensiones, existen isomorfismos excepcionales de grupos de Lie que producen formas adicionales de considerar simetrías de espacios hiperbólicos. Por ejemplo, en dimensión 2, los isomorfismos SO + (1, 2) ≅ PSL(2, R ) ≅ PSU(1, 1) permiten interpretar el modelo del semiplano superior como el cociente SL(2, R )/SO(2) y el modelo del disco de Poincaré como el cociente SU(1, 1)/U(1) . En ambos casos, los grupos de simetría actúan mediante transformaciones lineales fraccionarias, ya que ambos grupos son los estabilizadores que preservan la orientación en PGL(2, C ) de los respectivos subespacios de la esfera de Riemann. La transformación de Cayley no solo lleva un modelo del plano hiperbólico al otro, sino que realiza el isomorfismo de los grupos de simetría como conjugación en un grupo más grande. En dimensión 3, la acción lineal fraccionaria de PGL(2, C ) sobre la esfera de Riemann se identifica con la acción sobre el límite conforme del 3-espacio hiperbólico inducida por el isomorfismo O + (1, 3) ≅ PGL(2, C ) . Esto permite estudiar isometrías del 3-espacio hiperbólico considerando propiedades espectrales de matrices complejas representativas. Por ejemplo, las transformaciones parabólicas son conjugadas a traslaciones rígidas en el modelo de semiespacio superior, y son exactamente aquellas transformaciones que pueden representarse mediante matrices triangulares superiores unipotentes .
"Tres científicos, Ibn al-Haytham, Khayyam y al-Tūsī, habían hecho la contribución más considerable a esta rama de la geometría cuya importancia llegó a ser completamente reconocida solo en el siglo XIX. En esencia, sus proposiciones sobre las propiedades de los cuadrángulos que consideraron suponiendo que algunos de los ángulos de estas figuras eran agudos u obtusos, incorporaron los primeros teoremas de las geometrías hiperbólica y elíptica. Sus otras propuestas mostraron que varias afirmaciones geométricas eran equivalentes al postulado euclidiano V. Es extremadamente importante que estos eruditos establecieran la conexión mutua entre este postulado y la suma de los ángulos de un triángulo y un cuadrángulo. Con sus trabajos sobre la teoría de líneas paralelas, los matemáticos árabes influyeron directamente en las investigaciones relevantes de sus homólogos europeos. El primer intento europeo de demostrar el postulado sobre líneas paralelas, realizado por Witelo, el científico polaco del siglo XIII, mientras revisaba el Libro de Óptica de Ibn al-Haytham ( Kitab "La demostración de Euclides de Pseudo -Tusi se basó sin duda en fuentes árabes. Las pruebas presentadas en el siglo XIV por el erudito judío Levi ben Gerson , que vivió en el sur de Francia, y por el mencionado Alfonso de España, lindan directamente con la demostración de Ibn al-Haytham. Más arriba, hemos demostrado que la Exposición de Euclides de Pseudo-Tusi había estimulado los estudios de la teoría de las líneas paralelas tanto de J. Wallis como de G. Saccheri."
debemos a Lambert el primer desarrollo sistemático de la teoría de funciones hiperbólicas y, de hecho, nuestra notación actual para estas funciones.
el área de un triángulo hiperbólico es proporcional a su defecto angular apareció por primera vez en la monografía de Lambert Theorie der Parallellinien , que se publicó póstumamente en 1786.
De la nada he creado un universo nuevo y extraño. JÁNOS BOLYAI
{{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: others (link)