Cálculo discreto

Versión discreta (es decir, incremental) del cálculo infinitesimal

El cálculo discreto o el cálculo de funciones discretas , es el estudio matemático del cambio incremental , de la misma manera que la geometría es el estudio de la forma y el álgebra es el estudio de las generalizaciones de operaciones aritméticas . La palabra cálculo es una palabra latina que originalmente significa "pequeño guijarro"; Como estos guijarros se utilizaban para el cálculo, el significado de la palabra ha evolucionado y hoy suele significar un método de cálculo. Mientras tanto, el cálculo , originalmente llamado cálculo infinitesimal o "el cálculo de los infinitesimales ", es el estudio del cambio continuo .

El cálculo discreto tiene dos puntos de entrada, cálculo diferencial y cálculo integral. El cálculo diferencial se refiere a tasas de cambio incrementales y las pendientes de curvas lineales por partes. El cálculo integral se refiere a la acumulación de cantidades y las áreas bajo curvas constantes por partes. Estos dos puntos de vista están relacionados entre sí por el teorema fundamental del cálculo discreto.

El estudio de los conceptos de cambio comienza con su forma discreta. El desarrollo depende de un parámetro, el incremento de la variable independiente. Si así lo decidimos, podemos hacer que el incremento sea cada vez más pequeño y encontrar las contrapartes continuas de estos conceptos como límites . Informalmente, el límite del cálculo discreto es el cálculo infinitesimal. Aunque sirve como base discreta del cálculo, el valor principal del cálculo discreto está en las aplicaciones. ${\displaystyle \Delta x}$ ${\displaystyle \Delta x\to 0}$

Dos construcciones iniciales

El cálculo diferencial discreto es el estudio de la definición, propiedades y aplicaciones del cociente de diferencias de una función. El proceso de encontrar el cociente de diferencias se llama diferenciación . Dada una función definida en varios puntos de la recta real, el cociente de diferencias en ese punto es una forma de codificar el comportamiento a pequeña escala (es decir, del punto al siguiente) de la función. Al encontrar el cociente de diferencias de una función en cada par de puntos consecutivos en su dominio, es posible producir una nueva función, llamada función de cociente de diferencias o simplemente cociente de diferencias de la función original. En términos formales, el cociente de diferencias es un operador lineal que toma una función como entrada y produce una segunda función como salida. Esto es más abstracto que muchos de los procesos estudiados en álgebra elemental, donde las funciones generalmente ingresan un número y generan otro número. Por ejemplo, si a la función de duplicación se le da la entrada tres, entonces genera seis, y si a la función de cuadratura se le da la entrada tres, entonces genera nueve. La derivada, sin embargo, puede tomar la función de elevar al cuadrado como entrada. Esto significa que la derivada toma toda la información de la función elevatoria (por ejemplo, que dos se envía a cuatro, tres se envía a nueve, cuatro se envía a dieciséis, etc.) y utiliza esta información para producir otra función. La función producida al derivar la función de elevar al cuadrado resulta ser algo parecido a la función de duplicación.

Supongamos que las funciones están definidas en puntos separados por un incremento : ${\displaystyle \Delta x=h>0}$

${\displaystyle a,a+h,a+2h,\ldots ,a+nh,\ldots }$

La "función de duplicación" puede denotarse por y la "función de cuadratura" por . El "cociente de diferencias" es la tasa de cambio de la función en uno de los intervalos definidos por la fórmula: ${\displaystyle g(x)=2x}$ ${\displaystyle f(x)=x^{2}}$ ${\displaystyle [x,x+h]}$

${\displaystyle {\frac {f(x+h)-f(x)}{h}}.}$

Toma la función como entrada, es decir, toda la información (por ejemplo, que dos se envían a cuatro, tres se envían a nueve, cuatro se envían a dieciséis, etc.) y utiliza esta información para generar otra función, la función , como resultará. Por conveniencia, la nueva función puede definirse en los puntos medios de los intervalos anteriores: ${\displaystyle f}$ ${\displaystyle g(x)=2x+h}$

${\displaystyle a+h/2,a+h+h/2,a+2h+h/2,...,a+nh+h/2,...}$

Como la tasa de cambio es la de todo el intervalo , cualquier punto dentro de él puede usarse como referencia o, mejor aún, todo el intervalo que constituye el cociente de diferencias a - cocadena . ${\displaystyle [x,x+h]}$ ${\displaystyle 1}$

La notación más común para el cociente de diferencias es:

${\displaystyle {\frac {\Delta f}{\Delta x}}(x+h/2)={\frac {f(x+h)-f(x)}{h}}.}$

Si la entrada de la función representa el tiempo, entonces el cociente de diferencias representa el cambio con respecto al tiempo. Por ejemplo, si es una función que toma un tiempo como entrada y da la posición de una pelota en ese momento como salida, entonces el cociente de diferencias es cómo cambia la posición en el tiempo, es decir, es la velocidad de la pelota. . ${\displaystyle f}$ ${\displaystyle f}$

Si una función es lineal (es decir, si los puntos de la gráfica de la función se encuentran en una línea recta), entonces la función se puede escribir como , donde es la variable independiente, es la variable dependiente, es el intercepto y : ${\displaystyle y=mx+b}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle b}$ ${\displaystyle y}$

${\displaystyle m={\frac {\text{rise}}{\text{run}}}={\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {\Delta y}{\Delta x}}.}$

Pendiente: ${\displaystyle m={\frac {\Delta y}{\Delta x}}=\tan(\theta )}$

Esto da un valor exacto de la pendiente de una línea recta.

Sin embargo, si la función no es lineal, entonces el cambio en dividido por el cambio en varía. El cociente de diferencias da un significado exacto a la noción de cambio en la producción con respecto al cambio en los insumos. Para ser concretos, sea una función y fijemos un punto en el dominio de . es un punto en la gráfica de la función. Si es el incremento de , entonces es el siguiente valor de . Por tanto, es el incremento de . La pendiente de la recta entre estos dos puntos es ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle (x,f(x))}$ ${\displaystyle h}$ ${\displaystyle x}$ ${\displaystyle x+h}$ ${\displaystyle x}$ ${\displaystyle (x+h,f(x+h))}$ ${\displaystyle (x,f(x))}$

${\displaystyle m={\frac {f(x+h)-f(x)}{(x+h)-x}}={\frac {f(x+h)-f(x)}{h}}.}$

También lo es la pendiente de la recta entre y . ${\displaystyle m}$ ${\displaystyle (x,f(x))}$ ${\displaystyle (x+h,f(x+h))}$

Aquí hay un ejemplo particular, el cociente de diferencias de la función elevatoria. Sea la función elevatoria. Entonces: ${\displaystyle f(x)=x^{2}}$

${\displaystyle {\begin{aligned}{\frac {\Delta f}{\Delta x}}(x)&={(x+h)^{2}-x^{2} \over {h}}\\&={x^{2}+2hx+h^{2}-x^{2} \over {h}}\\&={2hx+h^{2} \over {h}}\\&=2x+h.\end{aligned}}}$

El cociente de diferencias del cociente de diferencias se llama segundo cociente de diferencias y se define en

${\displaystyle a+h,a+2h,a+3h,\ldots ,a+nh,\ldots }$

etcétera.

El cálculo integral discreto es el estudio de las definiciones, propiedades y aplicaciones de las sumas de Riemann . El proceso de encontrar el valor de una suma se llama integración . En lenguaje técnico, el cálculo integral estudia un determinado operador lineal .

La suma de Riemann ingresa una función y genera una función, que da la suma algebraica de áreas entre la parte de la gráfica de la entrada y el eje x .

Un ejemplo motivador son las distancias recorridas en un tiempo determinado.

${\displaystyle {\text{distance}}={\text{speed}}\cdot {\text{time}}}$

Si la velocidad es constante, sólo se necesita la multiplicación, pero si la velocidad cambia, evaluamos la distancia recorrida dividiendo el tiempo en muchos intervalos cortos de tiempo y luego multiplicando el tiempo transcurrido en cada intervalo por una de las velocidades en ese intervalo. , y luego tomando la suma (una suma de Riemann ) de la distancia recorrida en cada intervalo.

Velocidad constante

La suma de Riemann mide el área total de las barras, definida por , entre dos puntos (aquí y ). ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle b}$

Cuando la velocidad es constante, la distancia total recorrida durante el intervalo de tiempo dado se puede calcular multiplicando la velocidad y el tiempo. Por ejemplo, viajar a una velocidad constante de 50 mph durante 3 horas da como resultado una distancia total de 150 millas. En el diagrama de la izquierda, cuando se grafican la velocidad y el tiempo constantes, estos dos valores forman un rectángulo con una altura igual a la velocidad y un ancho igual al tiempo transcurrido. Por lo tanto, el producto de la velocidad y el tiempo también calcula el área rectangular bajo la curva de velocidad (constante). Esta conexión entre el área bajo una curva y la distancia recorrida se puede extender a cualquier región de forma irregular que exhiba una velocidad que varía incrementalmente durante un período de tiempo determinado. Si las barras en el diagrama de la derecha representan la velocidad a medida que varía de un intervalo al siguiente, la distancia recorrida (entre los tiempos representados por y ) es el área de la región sombreada . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle s}$

Entonces, el intervalo entre y se divide en una cantidad de segmentos iguales, la longitud de cada segmento representada por el símbolo . Para cada segmento pequeño, tenemos un valor de la función . Llame a ese valor . Luego, el área del rectángulo con base y altura da la distancia (tiempo multiplicado por la velocidad ) recorrida en ese segmento. Asociado a cada segmento está el valor de la función que está encima de él, . La suma de todos esos rectángulos da el área entre el eje y la curva constante por partes, que es la distancia total recorrida. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \Delta x}$ ${\displaystyle f(x)}$ ${\displaystyle v}$ ${\displaystyle \Delta x}$ ${\displaystyle v}$ ${\displaystyle \Delta x}$ ${\displaystyle v}$ ${\displaystyle f(x)=v}$

Supongamos que se define una función en los puntos medios de los intervalos de igual longitud : ${\displaystyle \Delta x=h>0}$

${\displaystyle a+h/2,a+h+h/2,a+2h+h/2,\ldots ,a+nh-h/2,\ldots }$

Entonces la suma de Riemann desde hasta en notación sigma es: ${\displaystyle a}$ ${\displaystyle b=a+nh}$

${\displaystyle \sum _{i=1}^{n}f(a+ih)\,\Delta x.}$

A medida que se realiza este cálculo para cada , la nueva función se define en los puntos: ${\displaystyle n}$

${\displaystyle a,a+h,a+2h,\ldots ,a+nh,\ldots }$

El teorema fundamental del cálculo establece que la diferenciación y la integración son operaciones inversas. Más precisamente, relaciona los cocientes de diferencias con las sumas de Riemann. También puede interpretarse como una afirmación precisa del hecho de que la diferenciación es lo inverso de la integración.

El teorema fundamental del cálculo: si una función está definida en una partición del intervalo , y si es una función cuyo cociente de diferencias es , entonces tenemos: ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle b=a+nh}$ ${\displaystyle F}$ ${\displaystyle f}$

${\displaystyle \sum _{i=0}^{n-1}f(a+ih+h/2)\,\Delta x=F(b)-F(a).}$

Además, para cada , tenemos: ${\textstyle m=0,1,2,\ldots ,n-1}$

${\displaystyle {\frac {\Delta }{\Delta x}}\sum _{i=0}^{m}f(a+ih+h/2)\,\Delta x=f(a+mh+h/2).}$

Esta es también una solución prototipo de una ecuación en diferencias . Las ecuaciones en diferencias relacionan una función desconocida con su diferencia o cociente de diferencias y son omnipresentes en las ciencias.

Historia

La historia temprana del cálculo discreto es la historia del cálculo . Ideas básicas como los cocientes de diferencias y las sumas de Riemann aparecen implícita o explícitamente en definiciones y demostraciones. Sin embargo, una vez superado el límite, nunca más se los volverá a ver. Sin embargo, la ley de voltaje de Kirchhoff (1847) se puede expresar en términos de la derivada exterior discreta unidimensional.

Durante el siglo XX, el cálculo discreto permanece interconectado con el cálculo infinitesimal, especialmente con sus formas diferenciales, pero también comienza a recurrir a la topología algebraica a medida que ambos se desarrollan. Las principales contribuciones provienen de las siguientes personas: ^[1]

• Henri Poincaré : triangulaciones ( subdivisión baricéntrica , triangulación dual ), lema de Poincaré , la primera prueba del teorema general de Stokes y mucho más
• LEJ Brouwer : teorema de aproximación simple
• Élie Cartan , Georges de Rham : la noción de forma diferencial, la derivada exterior como operador lineal independiente de las coordenadas , exactitud/cerrazón de las formas
• Emmy Noether , Heinz Hopf , Leopold Vietoris , Walther Mayer : módulos de cadenas , operador de frontera , complejos de cadenas
• JW Alexander , Solomon Lefschetz , Lev Pontryagin , Andrey Kolmogorov , Norman Steenrod , Eduard Čech : las primeras nociones de cocadena
• Hermann Weyl : las leyes de Kirchhoff expresadas en términos de los operadores de frontera y cofrontera
• WVD Hodge : el operador estrella de Hodge , la descomposición de Hodge
• Samuel Eilenberg , Saunders Mac Lane , Norman Steenrod , JHC Whitehead : el desarrollo riguroso de la teoría de la homología y la cohomología , incluidos los complejos de cadenas y cocadenas, el producto de copa
• Hassler Whitney : las cocadenas como integrandos

El reciente desarrollo del cálculo discreto, comenzando con Whitney, ha sido impulsado por las necesidades del modelado aplicado . ^{[2] [3] [4]}

Aplicaciones

El cálculo discreto se utiliza para modelar directa o indirectamente como una discretización del cálculo infinitesimal en todas las ramas de las ciencias físicas, ciencias actuariales , informática , estadística , ingeniería, economía, negocios, medicina, demografía y en otros campos donde un problema pueda resolverse. ser modelado matemáticamente . Permite pasar de tasas de cambio (no constantes) al cambio total o viceversa, y muchas veces al estudiar un problema conocemos uno y estamos tratando de encontrar el otro.

La física hace un uso particular del cálculo; Todos los conceptos discretos de la mecánica clásica y el electromagnetismo se relacionan mediante el cálculo discreto. La masa de un objeto de densidad conocida que varía incrementalmente, el momento de inercia de dichos objetos, así como la energía total de un objeto dentro de un campo conservador discreto, se pueden encontrar mediante el uso de cálculo discreto. Un ejemplo del uso del cálculo discreto en mecánica es la segunda ley del movimiento de Newton : históricamente expresada utiliza expresamente el término "cambio de movimiento" que implica el cociente de diferencias dicho El cambio de impulso de un cuerpo es igual a la fuerza resultante que actúa sobre el cuerpo y está en la misma dirección. Comúnmente expresado hoy como Fuerza = Masa × Aceleración, invoca el cálculo discreto cuando el cambio es incremental porque la aceleración es el cociente de diferencia de velocidad con respecto al tiempo o el segundo cociente de diferencia de la posición espacial. Partiendo de saber cómo se acelera un objeto, utilizamos las sumas de Riemann para derivar su trayectoria.

La teoría del electromagnetismo de Maxwell y la teoría de la relatividad general de Einstein se han expresado en el lenguaje del cálculo discreto.

La química utiliza el cálculo para determinar las velocidades de reacción y la desintegración radiactiva ( desintegración exponencial ).

En biología, la dinámica poblacional comienza con las tasas de reproducción y mortalidad para modelar los cambios poblacionales ( modelado poblacional ).

En ingeniería, las ecuaciones en diferencias se utilizan para trazar el rumbo de una nave espacial en entornos de gravedad cero, para modelar la transferencia de calor , la difusión y la propagación de ondas .

El análogo discreto del teorema de Green se aplica en un instrumento conocido como planímetro , que se utiliza para calcular el área de una superficie plana en un dibujo. Por ejemplo, se puede utilizar para calcular la cantidad de área ocupada por un parterre de flores de forma irregular o una piscina al diseñar el diseño de una propiedad. Se puede utilizar para calcular de manera eficiente sumas de dominios rectangulares en imágenes, para extraer características rápidamente y detectar objetos; Otro algoritmo que podría usarse es la tabla de áreas sumadas .

En el ámbito de la medicina, el cálculo se puede utilizar para encontrar el ángulo de ramificación óptimo de un vaso sanguíneo para maximizar el flujo. A partir de las leyes de desintegración para la eliminación de una droga en particular del cuerpo, se utiliza para derivar leyes de dosificación. En medicina nuclear, se utiliza para construir modelos de transporte de radiación en terapias tumorales dirigidas.

En economía, el cálculo permite determinar el beneficio máximo calculando tanto el costo marginal como el ingreso marginal , así como el modelado de mercados. ^[5]

En el procesamiento de señales y el aprendizaje automático, el cálculo discreto permite definiciones apropiadas de operadores (p. ej., convolución), optimización de conjuntos de niveles y otras funciones clave para el análisis de redes neuronales en estructuras gráficas. ^[3]

El cálculo discreto se puede utilizar junto con otras disciplinas matemáticas. Por ejemplo, se puede utilizar en teoría de la probabilidad para determinar la probabilidad de una variable aleatoria discreta a partir de una función de densidad supuesta.

Cálculo de diferencias y sumas.

Supongamos que una función (una -cochain) se define en puntos separados por un incremento : ${\displaystyle 0}$ ${\displaystyle f}$ ${\displaystyle \Delta x=h>0}$

${\displaystyle a,a+h,a+2h,\ldots ,a+nh,\ldots }$

La diferencia (o la derivada exterior , o el operador colímite) de la función viene dada por:

${\displaystyle {\big (}\Delta f{\big )}{\big (}[x,x+h]{\big )}=f(x+h)-f(x).}$

Se define en cada uno de los intervalos anteriores; es una -cocadena. ${\displaystyle 1}$

Supongamos que se define una cocadena en cada uno de los intervalos anteriores. Entonces su suma es una función (una -cocadena) definida en cada uno de los puntos por: ${\displaystyle 1}$ ${\displaystyle g}$ ${\displaystyle 0}$

${\displaystyle \left(\sum g\right)\!(a+nh)=\sum _{i=1}^{n}g{\big (}[a+(i-1)h,a+ih]{\big )}.}$

Estas son sus propiedades:

• Regla constante : si es una constante , entonces ${\displaystyle c}$

${\displaystyle \Delta c=0}$

• Linealidad : siyson constantes , ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle \Delta (af+bg)=a\,\Delta f+b\,\Delta g,\quad \sum (af+bg)=a\,\sum f+b\,\sum g}$

• Regla del producto :

${\displaystyle \Delta (fg)=f\,\Delta g+g\,\Delta f+\Delta f\,\Delta g}$

• Teorema fundamental del cálculo I :

${\displaystyle \left(\sum \Delta f\right)\!(a+nh)=f(a+nh)-f(a)}$

• Teorema fundamental del cálculo II :

${\displaystyle \Delta \!\left(\sum g\right)=g}$

Las definiciones se aplican a los gráficos de la siguiente manera. Si una función (una -cocadena) se define en los nodos de un gráfico: ${\displaystyle 0}$ ${\displaystyle f}$

${\displaystyle a,b,c,\ldots }$

entonces su derivada exterior (o el diferencial) es la diferencia, es decir, la siguiente función definida en los bordes del gráfico ( -cochain): ${\displaystyle 1}$

${\displaystyle \left(df\right)\!{\big (}[a,b]{\big )}=f(b)-f(a).}$

Si es una cocadena, entonces su integral sobre una secuencia de aristas del gráfico es la suma de sus valores sobre todas las aristas de ("integral de ruta"): ${\displaystyle g}$ ${\displaystyle 1}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma }$

${\displaystyle \int _{\sigma }g=\sum _{\sigma }g{\big (}[a,b]{\big )}.}$

Estas son las propiedades:

• Regla constante : si es una constante , entonces ${\displaystyle c}$

${\displaystyle dc=0}$

• Linealidad : si y son constantes , ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle d(af+bg)=a\,df+b\,dg,\quad \int _{\sigma }(af+bg)=a\,\int _{\sigma }f+b\,\int _{\sigma }g}$

• Regla del producto :

${\displaystyle d(fg)=f\,dg+g\,df+df\,dg}$

• Teorema fundamental del cálculo I : si una cadena consta de aristas , entonces para cualquier cocadena ${\displaystyle 1}$ ${\displaystyle \sigma }$ ${\displaystyle [a_{0},a_{1}],[a_{1},a_{2}],...,[a_{n-1},a_{n}]}$ ${\displaystyle 0}$ ${\displaystyle f}$

${\displaystyle \int _{\sigma }df=f(a_{n})-f(a_{0})}$

• Teorema fundamental del cálculo II : si el gráfico es un árbol , es una -cocadena, y una función ( -cocadena) está definida en los nodos del gráfico por ${\displaystyle g}$ ${\displaystyle 1}$ ${\displaystyle 0}$

${\displaystyle f(x)=\int _{\sigma }g}$

donde una cadena consiste en algo fijo , entonces ${\displaystyle 1}$ ${\displaystyle \sigma }$ ${\displaystyle [a_{0},a_{1}],[a_{1},a_{2}],...,[a_{n-1},x]}$ ${\displaystyle a_{0}}$

${\displaystyle df=g}$

Ver referencias. ^{[6] [7] [8] [9] [3] [10]}

Cadenas de simples y cubos.

Un complejo simplista.

Un complejo simplicial es un conjunto de simples que satisface las siguientes condiciones: ${\displaystyle S}$

1. Cada cara de un simplex de también está en . ${\displaystyle S}$ ${\displaystyle S}$

2. La intersección no vacía de dos simples cualesquiera es una cara de ambos y . ${\displaystyle \sigma _{1},\sigma _{2}\in S}$ ${\displaystyle \sigma _{1}}$ ${\displaystyle \sigma _{2}}$

Se toman el límite de un límite de 2 simplex (izquierda) y el límite de una cadena 1 (derecha). Ambos son 0, siendo sumas en las que tanto el positivo como el negativo de un 0-símplex ocurren una vez. El límite de un límite es siempre 0. Un ciclo no trivial es algo que se cierra como el límite de un simplex, en el sentido de que su límite suma 0, pero que en realidad no es el límite de un simplex o cadena.

Por definición, una orientación de un k -simplex viene dada por un ordenamiento de los vértices, escrito como , con la regla de que dos ordenamientos definen la misma orientación si y sólo si difieren por una permutación par . Por lo tanto, cada simplex tiene exactamente dos orientaciones y cambiar el orden de dos vértices cambia una orientación a la orientación opuesta. Por ejemplo, elegir una orientación de un 1-símplex equivale a elegir una de las dos direcciones posibles, y elegir una orientación de un 2-símplex equivale a elegir lo que debería significar "en sentido contrario a las agujas del reloj". ${\displaystyle (v_{0},...,v_{k})}$

Sea un complejo simple. Una k -cadena simplicial es una suma formal finita ${\displaystyle S}$

${\displaystyle \sum _{i=1}^{N}c_{i}\sigma _{i},\,}$

donde cada _ci es un número entero y σ _i es un k -símplex orientado. En esta definición, declaramos que cada simplex orientado es igual al negativo del simplex con la orientación opuesta. Por ejemplo,

${\displaystyle (v_{0},v_{1})=-(v_{1},v_{0}).}$

El espacio vectorial de k -cadenas está escrito . Tiene una base en correspondencia uno a uno con el conjunto de k -simplices en . Para definir una base explícitamente, hay que elegir una orientación de cada simplex. Una forma estándar de hacer esto es elegir un orden de todos los vértices y darle a cada simplex la orientación correspondiente al orden inducido de sus vértices. ${\displaystyle S}$ ${\displaystyle C_{k}}$ ${\displaystyle S}$

Sea un k -simplex orientado, visto como un elemento base de . El operador de frontera ${\displaystyle \sigma =(v_{0},...,v_{k})}$ ${\displaystyle C_{k}}$

${\displaystyle \partial _{k}:C_{k}\rightarrow C_{k-1}}$

es el operador lineal definido por:

${\displaystyle \partial _{k}(\sigma )=\sum _{i=0}^{k}(-1)^{i}(v_{0},\dots ,{\widehat {v_{i}}},\dots ,v_{k}),}$

donde el simplex orientado

${\displaystyle (v_{0},\dots ,{\widehat {v_{i}}},\dots ,v_{k})}$

es la enésima cara de , obtenida eliminando su enésimo vértice. ${\displaystyle i}$ ${\displaystyle \sigma }$ ${\displaystyle i}$

En , elementos del subgrupo ${\displaystyle C_{k}}$

${\displaystyle Z_{k}=\ker \partial _{k}}$

se conocen como ciclos , y el subgrupo

${\displaystyle B_{k}=\operatorname {im} \partial _{k+1}}$

Se dice que está formado por fronteras .

Un cálculo directo muestra que . En términos geométricos, esto dice que el límite de cualquier cosa no tiene límite. De manera equivalente, los espacios vectoriales forman un complejo de cadenas . Otra afirmación equivalente es la que está contenida en . ${\displaystyle \partial ^{2}=0}$ ${\displaystyle (C_{k},\partial _{k})}$ ${\displaystyle B_{k}}$ ${\displaystyle Z_{k}}$

Un complejo cúbico es un conjunto compuesto de puntos , segmentos de línea , cuadrados , cubos y sus contrapartes de n dimensiones . Se utilizan de manera análoga a los simples para formar complejos. Un intervalo elemental es un subconjunto de la forma ${\displaystyle I\subset \mathbf {R} }$

${\displaystyle I=[\ell ,\ell +1]\quad {\text{or}}\quad I=[\ell ,\ell ]}$

para algunos . Un cubo elemental es el producto finito de intervalos elementales, es decir ${\displaystyle \ell \in \mathbf {Z} }$ ${\displaystyle Q}$

${\displaystyle Q=I_{1}\times I_{2}\times \cdots \times I_{d}\subset \mathbf {R} ^{d}}$

¿ Dónde están los intervalos elementales? De manera equivalente, un cubo elemental es cualquier traducción de un cubo unitario incrustado en el espacio euclidiano (para algunos con ). Un conjunto es un complejo cúbico si puede escribirse como una unión de cubos elementales (o posiblemente, es homeomorfo a dicho conjunto) y contiene todas las caras de todos sus cubos. El operador de frontera y el complejo de cadena se definen de manera similar a los de los complejos simpliciales. ${\displaystyle I_{1},I_{2},\ldots ,I_{d}}$ ${\displaystyle [0,1]^{n}}$ ${\displaystyle \mathbf {R} ^{d}}$ ${\displaystyle n,d\in \mathbf {N} \cup \{0\}}$ ${\displaystyle n\leq d}$ ${\displaystyle X\subseteq \mathbf {R} ^{d}}$

Más generales son los complejos celulares .

Un complejo de cadenas es una secuencia de espacios vectoriales conectados por operadores lineales (llamados operadores de límite ) , de modo que la composición de dos mapas consecutivos cualesquiera es el mapa cero. Explícitamente, los operadores de límite satisfacen , o con índices suprimidos ,. El complejo puede escribirse de la siguiente manera. ${\displaystyle (C_{*},\partial _{*})}$ ${\displaystyle \ldots ,C_{0},C_{1},C_{2},C_{3},C_{4},\ldots }$ ${\displaystyle \partial _{n}:C_{n}\to C_{n-1}}$ ${\displaystyle \partial _{n}\circ \partial _{n+1}=0}$ ${\displaystyle \partial ^{2}=0}$

${\displaystyle \cdots {\xleftarrow {\partial _{0}}}C_{0}{\xleftarrow {\partial _{1}}}C_{1}{\xleftarrow {\partial _{2}}}C_{2}{\xleftarrow {\partial _{3}}}C_{3}{\xleftarrow {\partial _{4}}}C_{4}{\xleftarrow {\partial _{5}}}\cdots }$

Un mapa simplicial es un mapa entre complejos simpliciales con la propiedad de que las imágenes de los vértices de un simplex siempre abarcan un simplex (por lo tanto, los vértices tienen vértices para imágenes). Un mapa simplicial de un complejo simplicial a otro es una función del conjunto de vértices de al conjunto de vértices de tal que la imagen de cada simplex en (visto como un conjunto de vértices) es un simplex en . Genera un mapa lineal, llamado mapa de cadena , desde el complejo de cadena de hasta el complejo de cadena de . Explícitamente, está dado en cadenas por ${\displaystyle f}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle k}$

${\displaystyle f((v_{0},\ldots ,v_{k}))=(f(v_{0}),\ldots ,f(v_{k}))}$

si son todos distintos y, en caso contrario, se establece igual a . ${\displaystyle f(v_{0}),...,f(v_{k})}$ ${\displaystyle 0}$

Un mapa de cadenas entre dos complejos de cadenas y es una secuencia de homomorfismos para cada uno que conmuta con los operadores de frontera en los dos complejos de cadenas, entonces . Esto se expresa en el siguiente diagrama conmutativo : ${\displaystyle f}$ ${\displaystyle (A_{*},d_{A,*})}$ ${\displaystyle (B_{*},d_{B,*})}$ ${\displaystyle f_{*}}$ ${\displaystyle f_{n}:A_{n}\rightarrow B_{n}}$ ${\displaystyle n}$ ${\displaystyle d_{B,n}\circ f_{n}=f_{n-1}\circ d_{A,n}}$

Un mapa de cadenas envía ciclos a ciclos y límites a límites.

Ver referencias. ^{[11] [10] [12]}

Formas diferenciales discretas: cocadenas

Para cada espacio vectorial Ci en el complejo _de cadenas consideramos su espacio dual y es su operador lineal dual. ${\displaystyle C_{i}^{*}:=\mathrm {Hom} (C_{i},{\bf {R}}),}$ ${\displaystyle d^{i}=\partial _{i}^{*}}$

${\displaystyle d^{i-1}:C_{i-1}^{*}\to C_{i}^{*}.}$

Esto tiene el efecto de "invertir todas las flechas" del complejo original, dejando un complejo de cocadena.

${\displaystyle \cdots \leftarrow C_{i+1}^{*}{\stackrel {\partial _{i}^{*}}{\leftarrow }}\ C_{i}^{*}{\stackrel {\partial _{i-1}^{*}}{\leftarrow }}C_{i-1}^{*}\leftarrow \cdots }$

El complejo de cocadena es la noción dual de complejo de cadena. Consiste en una secuencia de espacios vectoriales conectados por operadores lineales que satisfacen . El complejo de cocadena se puede escribir de forma similar al complejo de cadena. ${\displaystyle (C^{*},d^{*})}$ ${\displaystyle ...,C_{0},C_{1},C_{2},C_{3},C_{4},...}$ ${\displaystyle d^{n}:C^{n}\to C^{n+1}}$ ${\displaystyle d^{n+1}\circ d^{n}=0}$

${\displaystyle \cdots {\xrightarrow {d^{-1}}}C^{0}{\xrightarrow {d^{0}}}C^{1}{\xrightarrow {d^{1}}}C^{2}{\xrightarrow {d^{2}}}C^{3}{\xrightarrow {d^{3}}}C^{4}{\xrightarrow {d^{4}}}\cdots }$

El índice en o se conoce como grado (o dimensión ). La diferencia entre complejos de cadena y cocadena es que, en los complejos de cadena, los diferenciales disminuyen la dimensión, mientras que en los complejos de cocadena aumentan la dimensión. ${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle C^{n}}$

Los elementos de los espacios vectoriales individuales de un complejo de (co)cadenas se denominan cocadenas . Los elementos en el núcleo de se llaman cociclos (o elementos cerrados ), y los elementos en la imagen de se llaman colímites (o elementos exactos ). Desde la definición de diferencial, todos los límites son ciclos. ${\displaystyle d}$ ${\displaystyle d}$

El lema de Poincaré establece que si es una bola abierta en , cualquier forma cerrada definida en es exacta, para cualquier número entero con . ${\displaystyle B}$ ${\displaystyle {\bf {R}}^{n}}$ ${\displaystyle p}$ ${\displaystyle \omega }$ ${\displaystyle B}$ ${\displaystyle p}$ ${\displaystyle 1\leq p\leq n}$

Cuando nos referimos a las cocadenas como formas discretas (diferenciales) , nos referimos a ellas como derivadas exteriores . También utilizamos la notación de cálculo para los valores de las formas: ${\displaystyle d}$

${\displaystyle \omega (s)=\int _{s}\omega .}$

El teorema de Stokes es una afirmación sobre las formas diferenciales discretas en variedades , que generaliza el teorema fundamental del cálculo discreto para una partición de un intervalo:

${\displaystyle \sum _{i=0}^{n-1}{\frac {\Delta F}{\Delta x}}(a+ih+h/2)\,\Delta x=F(b)-F(a).}$

El teorema de Stokes dice que la suma de una forma sobre el límite de alguna variedad orientable es igual a la suma de su derivada exterior sobre la totalidad de , es decir, ${\displaystyle \omega }$ ${\displaystyle \Omega }$ ${\displaystyle d\omega }$ ${\displaystyle \Omega }$

${\displaystyle \int _{\Omega }d\omega =\int _{\partial \Omega }\omega \,.}$

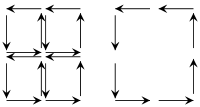
Vale la pena examinar el principio subyacente considerando un ejemplo de dimensiones. La idea esencial se puede entender en el diagrama de la izquierda, que muestra que, en un mosaico orientado de una variedad, los caminos interiores se atraviesan en direcciones opuestas; sus contribuciones a la integral de trayectoria se cancelan entre sí por pares. Como consecuencia, sólo queda la contribución de la frontera. ${\displaystyle d=2}$

Ver referencias. ^{[11] [10]}

El producto cuña de las formas.

En cálculo discreto, esta es una construcción que crea a partir de formas formas de orden superior: unir dos cocadenas de grado y formar una cocadena compuesta de grado . ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle p+q}$

Para complejos cúbicos , el producto cuña se define en cada cubo visto como un espacio vectorial de la misma dimensión.

Para complejos simpliciales , el producto cuña se implementa como producto copa : si es una -cocadena y es una -cocadena, entonces ${\displaystyle f^{p}}$ ${\displaystyle p}$ ${\displaystyle g^{q}}$ ${\displaystyle q}$

${\displaystyle (f^{p}\smile g^{q})(\sigma )=f^{p}(\sigma _{0,1,...,p})\cdot g^{q}(\sigma _{p,p+1,...,p+q})}$

donde es a -simplex y , es el simplex dividido en el -simplex cuyos vértices están indexados por . Entonces, es la -ésima cara frontal y la -ésima cara posterior de , respectivamente. ${\displaystyle \sigma }$ ${\displaystyle (p+q)}$ ${\displaystyle \sigma _{S},\ S\subset \{0,1,...,p+q\}}$ ${\displaystyle S}$ ${\displaystyle (p+q)}$ ${\displaystyle \{0,...,p+q\}}$ ${\displaystyle \sigma _{0,1,...,p}}$ ${\displaystyle p}$ ${\displaystyle \sigma _{p,p+1,...,p+q}}$ ${\displaystyle q}$ ${\displaystyle \sigma }$

El colímite del producto de copa de las cocadenas y está dado por ${\displaystyle f^{p}}$ ${\displaystyle g^{q}}$

${\displaystyle d(f^{p}\smile g^{q})=d{f^{p}}\smile g^{q}+(-1)^{p}(f^{p}\smile d{g^{q}}).}$

El producto de taza de dos cociclos es nuevamente un cociclo, y el producto de un colímite con un cociclo (en cualquier orden) es un colímite.

La operación del producto en taza satisface la identidad.

${\displaystyle \alpha ^{p}\smile \beta ^{q}=(-1)^{pq}(\beta ^{q}\smile \alpha ^{p}).}$

En otras palabras, la multiplicación correspondiente es conmutativa graduada .

Ver referencias. ^[11]

operador de Laplace

El operador de Laplace de una función en un vértice es (hasta un factor) la velocidad a la que el valor promedio de sobre una vecindad celular de se desvía de . El operador de Laplace representa la densidad de flujo del flujo gradiente de una función. Por ejemplo, la velocidad neta a la que una sustancia química disuelta en un fluido se acerca o se aleja de algún punto es proporcional al operador de Laplace de la concentración química en ese punto; expresada simbólicamente, la ecuación resultante es la ecuación de difusión . Por estas razones, se utiliza ampliamente en las ciencias para modelar diversos fenómenos físicos. ${\displaystyle \Delta f}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle f(p)}$

El codiferencial

${\displaystyle \delta :C^{k}\to C^{k-1}}$

es un operador definido en -forms por: ${\displaystyle k}$

${\displaystyle \delta =(-1)^{n(k-1)+1}{\star }d{\star }=(-1)^{k}\,{\star }^{-1}d{\star },}$

donde es la derivada o diferencial exterior y es el operador estrella de Hodge . ${\displaystyle d}$ ${\displaystyle \star }$

El codiferencial es el adjunto de la derivada exterior según el teorema de Stokes:

${\displaystyle (\eta ,\delta \zeta )=(d\eta ,\zeta ).}$

Dado que el diferencial satisface , el codiferencial tiene la propiedad correspondiente ${\displaystyle d^{2}=0}$

${\displaystyle \delta ^{2}={\star }d{\star }{\star }d{\star }=(-1)^{k(n-k)}{\star }d^{2}{\star }=0.}$

El operador de Laplace se define por:

${\displaystyle \Delta =(\delta +d)^{2}=\delta d+d\delta .}$

Ver referencias. ^[10]

Relacionado

• Método de elementos discretos
• Diferencias divididas
• Coeficiente de diferencias finitas
• método de diferencias finitas
• Método de elementos finitos
• Método de volumen finito
• Diferenciación numérica
• Integracion numerica
• Métodos numéricos para ecuaciones diferenciales ordinarias.

Ver también

• Cálculo de diferencias finitas
• Cálculo sobre gráficos ponderados finitos
• autómata celular
• Geometría diferencial discreta
• Operador discreto de Laplace
• Cálculo de diferencias finitas, cálculo discreto o análisis discreto
• Teoría de Morse discreta

Referencias

1. Dieudonné, Jean (1988). Una historia de la topología algebraica y diferencial 1900-1960. Birkhäuser Boston. ISBN 9780817649074.
2. Auclair-Fortier, Marie-Flavie; Ziou, Djemel; Allili, Madjid (2004). "Enfoque de topología algebraica computacional global para difusión". En Bouman, Charles A; Miller, Eric L (eds.). Imágenes Computacionales II . vol. 5299. ESPÍA. pag. 357. doi : 10.1117/12.525975. S2CID  2211593.
3. Grady, Leo; Polimeni, Jonathan (2011). Cálculo discreto: análisis aplicado de gráficos para ciencias computacionales (PDF) . Saltador.
4. Desbrun, Mathieu; Kanso, Eva ; Tong, Yiying (2008). "Formas diferenciales discretas para modelado computacional". En Bobenko, AI; Sullivan, JM; Schröder, P.; Ziegler, GM (eds.). Geometría Diferencial Discreta . Seminarios de Oberwolfach. vol. 38. Basilea: Birkhäuser.
5. Wilmott, Pablo; Howison, Sam; Dewynne, Jeff (1995). Las matemáticas de los derivados financieros: una introducción para el estudiante . Prensa de la Universidad de Cambridge. pag. 137.ISBN​ 978-0-521-49789-3.
6. Chaudhry, M. Hanif (2007). Flujo de canal abierto . Saltador. pag. 369.ISBN​ 978-0-387-68648-6.
7. Levy, H.; Lessman, F. (1992). Ecuaciones en diferencias finitas . Publicaciones de Dover. ISBN 0-486-67260-3.
8. Ames, WF (1977). "Sección 1.6". Métodos numéricos para ecuaciones diferenciales parciales . Prensa académica. ISBN 0-12-056760-1.
9. Hildebrand, FB (1968). "Sección 2.2". Simulaciones y ecuaciones en diferencias finitas. Prentice Hall. OCLC  780785195.
10. Saveliev, Peter (2016). Topología ilustrada . Peter Saveliev. ISBN 978-1495188756.
11. Bredon, Glen E. (1997). Topología y Geometría . Textos de Posgrado en Matemáticas. Saltador. ISBN 0387979263.
12. Kaczynski, Tomasz; Mischaikow, Konstantin; Mrozek, Marian (2004). Topología Computacional . ISBN 0-387-40853-3.