Valores propios y vectores propios

Conceptos de álgebra lineal

En álgebra lineal , un vector propio ( / ˈaɪɡən- / EYE -gən- ) o vector característico es un vector cuya dirección no cambia con una transformación lineal dada . Más precisamente, un vector propio, , de una transformación lineal, , se escala por un factor constante , , cuando se le aplica la transformación lineal: . A menudo es importante conocer estos vectores en álgebra lineal. El valor propio correspondiente , valor característico o raíz característica es el factor multiplicador . ${\displaystyle \mathbf {v} }$ ${\displaystyle T}$ ${\displaystyle \lambda }$ ${\displaystyle T\mathbf {v} =\lambda \mathbf {v} }$ ${\displaystyle \lambda }$

Geométricamente, los vectores son cantidades multidimensionales con magnitud y dirección, a menudo representadas como flechas. Una transformación lineal rota , estira o corta los vectores sobre los que actúa. Sus vectores propios son aquellos vectores que solo se estiran, sin rotación ni corte. El valor propio correspondiente es el factor por el cual un vector propio se estira o se aplasta. Si el valor propio es negativo, la dirección del vector propio se invierte. ^[1]

Los vectores y valores propios de una transformación lineal sirven para caracterizarla, por lo que desempeñan papeles importantes en todas las áreas en las que se aplica el álgebra lineal, desde la geología hasta la mecánica cuántica . En particular, a menudo se da el caso de que un sistema se representa mediante una transformación lineal cuyas salidas se introducen como entradas a la misma transformación ( retroalimentación ). En una aplicación de este tipo, el valor propio más grande es de particular importancia, porque gobierna el comportamiento a largo plazo del sistema después de muchas aplicaciones de la transformación lineal, y el vector propio asociado es el estado estacionario del sistema.

Definición

Consideremos una matriz A y un vector distinto de cero de longitud Si multiplicar A por (denotado por ) simplemente escala por un factor de λ , donde λ es un escalar , entonces se llama vector propio de A , y λ es el valor propio correspondiente. Esta relación se puede expresar como: . ^[2] ${\displaystyle n{\times }n}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle n.}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle A\mathbf {v} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle A\mathbf {v} =\lambda \mathbf {v} }$

Existe una correspondencia directa entre matrices cuadradas de n por n y transformaciones lineales de un espacio vectorial de n dimensiones a sí mismo, dada cualquier base del espacio vectorial. Por lo tanto, en un espacio vectorial de dimensión finita, es equivalente definir valores propios y vectores propios utilizando el lenguaje de matrices o el lenguaje de transformaciones lineales. ^{[3] [4]}

La siguiente sección ofrece un punto de vista más general que también cubre los espacios vectoriales de dimensión infinita .

Descripción general

Los valores propios y los vectores propios ocupan un lugar destacado en el análisis de las transformaciones lineales. El prefijo eigen- se adopta de la palabra alemana eigen ( cognado de la palabra inglesa own ) para 'apropiado', 'característico', 'propio'. ^{[5] [6]} Originalmente utilizados para estudiar los ejes principales del movimiento rotacional de cuerpos rígidos , los valores propios y los vectores propios tienen una amplia gama de aplicaciones, por ejemplo en el análisis de estabilidad , análisis de vibraciones , orbitales atómicos , reconocimiento facial y diagonalización de matrices .

En esencia, un vector propio v de una transformación lineal T es un vector distinto de cero que, cuando se le aplica T , no cambia de dirección. La aplicación de T al vector propio solo escala el vector propio por el valor escalar λ , llamado valor propio. Esta condición se puede escribir como la ecuación denominada ecuación de valor propio o ecuación propia . En general, λ puede ser cualquier escalar . Por ejemplo, λ puede ser negativo, en cuyo caso el vector propio invierte la dirección como parte del escalamiento, o puede ser cero o complejo . $${\displaystyle T(\mathbf {v} )=\lambda \mathbf {v} ,}$$

En esta aplicación de cizallamiento, la flecha roja cambia de dirección, pero la flecha azul no. La flecha azul es un vector propio de esta aplicación de cizallamiento porque no cambia de dirección y, dado que su longitud no cambia, su valor propio es 1.

Matriz real y simétrica de 2×2 que representa un estiramiento y un corte del plano. Los vectores propios de la matriz (líneas rojas) son las dos direcciones especiales de modo que cada punto de ellas se deslice sobre ellas.

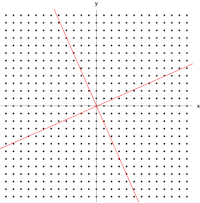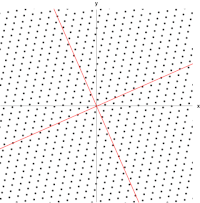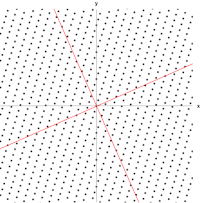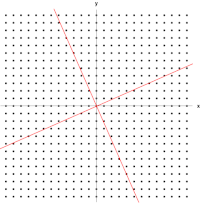
El ejemplo que se muestra aquí, basado en la Mona Lisa , proporciona una ilustración sencilla. Cada punto de la pintura se puede representar como un vector que apunta desde el centro de la pintura hasta ese punto. La transformación lineal en este ejemplo se llama mapeo de cizallamiento . Los puntos en la mitad superior se mueven hacia la derecha y los puntos en la mitad inferior se mueven hacia la izquierda, de manera proporcional a la distancia que se encuentran del eje horizontal que pasa por el medio de la pintura. Por lo tanto, los vectores que apuntan a cada punto en la imagen original se inclinan hacia la derecha o hacia la izquierda y se alargan o acortan mediante la transformación. Los puntos a lo largo del eje horizontal no se mueven en absoluto cuando se aplica esta transformación. Por lo tanto, cualquier vector que apunte directamente a la derecha o a la izquierda sin componente vertical es un vector propio de esta transformación, porque el mapeo no cambia su dirección. Además, todos estos vectores propios tienen un valor propio igual a uno, porque el mapeo tampoco cambia su longitud.

Las transformaciones lineales pueden tomar muchas formas diferentes, mapeando vectores en una variedad de espacios vectoriales, por lo que los vectores propios también pueden tomar muchas formas. Por ejemplo, la transformación lineal podría ser un operador diferencial como , en cuyo caso los vectores propios son funciones llamadas funciones propias que son escaladas por ese operador diferencial, como Alternativamente, la transformación lineal podría tomar la forma de una matriz n por n , en cuyo caso los vectores propios son matrices n por 1. Si la transformación lineal se expresa en la forma de una matriz n por n A , entonces la ecuación de valor propio para una transformación lineal anterior se puede reescribir como la multiplicación de matrices donde el vector propio v es una matriz n por 1. Para una matriz, los valores propios y los vectores propios se pueden usar para descomponer la matriz , por ejemplo, diagonalizándola . ${\displaystyle {\tfrac {d}{dx}}}$ $${\displaystyle {\frac {d}{dx}}e^{\lambda x}=\lambda e^{\lambda x}.}$$ $${\displaystyle A\mathbf {v} =\lambda \mathbf {v} ,}$$

Los valores propios y los vectores propios dan lugar a muchos conceptos matemáticos estrechamente relacionados, y el prefijo eigen- se aplica generosamente al nombrarlos:

• El conjunto de todos los vectores propios de una transformación lineal, cada uno emparejado con su valor propio correspondiente, se denomina sistema propio de esa transformación. ^{[7] [8]}
• El conjunto de todos los vectores propios de T correspondientes al mismo valor propio, junto con el vector cero, se denomina espacio propio , o el espacio característico de T asociado con ese valor propio. ^[9]
• Si un conjunto de vectores propios de T forma una base del dominio de T , entonces esta base se denomina base propia .

Historia

Los valores propios suelen introducirse en el contexto del álgebra lineal o la teoría de matrices . Sin embargo, históricamente, surgieron en el estudio de formas cuadráticas y ecuaciones diferenciales .

En el siglo XVIII, Leonhard Euler estudió el movimiento de rotación de un cuerpo rígido y descubrió la importancia de los ejes principales . ^[a] Joseph-Louis Lagrange se dio cuenta de que los ejes principales son los vectores propios de la matriz de inercia. ^[10]

A principios del siglo XIX, Augustin-Louis Cauchy vio cómo su trabajo podía usarse para clasificar las superficies cuadráticas y lo generalizó a dimensiones arbitrarias. ^[11] Cauchy también acuñó el término racine caractéristique (raíz característica), para lo que ahora se llama valor propio ; su término sobrevive en la ecuación característica . ^[b]

Más tarde, Joseph Fourier utilizó el trabajo de Lagrange y Pierre-Simon Laplace para resolver la ecuación del calor por separación de variables en su famoso libro de 1822 Théorie analytique de la chaleur . ^[12] Charles-François Sturm desarrolló aún más las ideas de Fourier y las llevó a la atención de Cauchy, quien las combinó con sus propias ideas y llegó al hecho de que las matrices simétricas reales tienen valores propios reales. ^[11] Esto fue extendido por Charles Hermite en 1855 a lo que ahora se llaman matrices hermíticas . ^[13]

Casi al mismo tiempo, Francesco Brioschi demostró que los valores propios de las matrices ortogonales se encuentran en el círculo unitario ^[11] y Alfred Clebsch encontró el resultado correspondiente para matrices antisimétricas ^[13] . Finalmente, Karl Weierstrass aclaró un aspecto importante en la teoría de estabilidad iniciada por Laplace, al darse cuenta de que las matrices defectuosas pueden causar inestabilidad ^[11] .

Mientras tanto, Joseph Liouville estudió problemas de valores propios similares a los de Sturm; la disciplina que surgió de su trabajo ahora se llama teoría de Sturm-Liouville . ^[14] Schwarz estudió el primer valor propio de la ecuación de Laplace en dominios generales hacia fines del siglo XIX, mientras que Poincaré estudió la ecuación de Poisson unos años más tarde. ^[15]

A principios del siglo XX, David Hilbert estudió los valores propios de los operadores integrales al considerarlos como matrices infinitas. ^[16] Fue el primero en utilizar la palabra alemana eigen , que significa "propio", ^[6] para denotar valores propios y vectores propios en 1904, ^[c] aunque es posible que haya seguido un uso relacionado de Hermann von Helmholtz . Durante algún tiempo, el término estándar en inglés era "valor propio", pero el término más distintivo "valor propio" es el estándar en la actualidad. ^[17]

El primer algoritmo numérico para calcular valores y vectores propios apareció en 1929, cuando Richard von Mises publicó el método de potencia . Uno de los métodos más populares en la actualidad, el algoritmo QR , fue propuesto independientemente por John GF Francis ^[18] y Vera Kublanovskaya ^[19] en 1961. ^{[20] [21]}

Valores propios y vectores propios de matrices

Los valores y vectores propios suelen presentarse a los estudiantes en el contexto de cursos de álgebra lineal centrados en matrices. ^{[22] [23]} Además, las transformaciones lineales sobre un espacio vectorial de dimensión finita se pueden representar utilizando matrices, ^{[3] [4]} lo que es especialmente común en aplicaciones numéricas y computacionales. ^[24]

La matriz A actúa estirando el vector x , sin cambiar su dirección, por lo que x es un vector propio de A .

Consideremos vectores n -dimensionales que se forman como una lista de n escalares, como los vectores tridimensionales $${\displaystyle \mathbf {x} ={\begin{bmatrix}1\\-3\\4\end{bmatrix}}\quad {\mbox{and}}\quad \mathbf {y} ={\begin{bmatrix}-20\\60\\-80\end{bmatrix}}.}$$

Se dice que estos vectores son múltiplos escalares entre sí, o paralelos o colineales , si existe un escalar λ tal que $${\displaystyle \mathbf {x} =\lambda \mathbf {y} .}$$

En este caso, . ${\displaystyle \lambda =-{\frac {1}{20}}}$

Consideremos ahora la transformación lineal de vectores n -dimensionales definidos por una matriz n por n A , o donde, para cada fila, $${\displaystyle A\mathbf {v} =\mathbf {w} ,}$$ $${\displaystyle {\begin{bmatrix}A_{11}&A_{12}&\cdots &A_{1n}\\A_{21}&A_{22}&\cdots &A_{2n}\\\vdots &\vdots &\ddots &\vdots \\A_{n1}&A_{n2}&\cdots &A_{nn}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}={\begin{bmatrix}w_{1}\\w_{2}\\\vdots \\w_{n}\end{bmatrix}}}$$ $${\displaystyle w_{i}=A_{i1}v_{1}+A_{i2}v_{2}+\cdots +A_{in}v_{n}=\sum _{j=1}^{n}A_{ij}v_{j}.}$$

Si ocurre que v y w son múltiplos escalares, es decir si

entonces v es un vector propio de la transformación lineal A y el factor de escala λ es el valor propio correspondiente a ese vector propio. La ecuación ( 1 ) es la ecuación del valor propio para la matriz A.

La ecuación ( 1 ) se puede expresar de manera equivalente como

donde I es la matriz identidad n por n y 0 es el vector cero.

Valores propios y polinomio característico

La ecuación ( 2 ) tiene una solución v distinta de cero si y solo si el determinante de la matriz ( A − λI ) es cero. Por lo tanto, los valores propios de A son valores de λ que satisfacen la ecuación

Utilizando la fórmula de Leibniz para determinantes , el lado izquierdo de la ecuación ( 3 ) es una función polinómica de la variable λ y el grado de este polinomio es n , el orden de la matriz A. Sus coeficientes dependen de las entradas de A , excepto que su término de grado n es siempre (−1) n ^λ n ^. Este polinomio se denomina polinomio característico de A. La ecuación ( 3 ) se denomina ecuación característica o ecuación secular de A.

El teorema fundamental del álgebra implica que el polinomio característico de una matriz n por n A , al ser un polinomio de grado n , puede factorizarse en el producto de n términos lineales,

donde cada λ _i puede ser real pero en general es un número complejo. Los números λ ₁ , λ ₂ , ..., λ _n , que pueden no tener todos valores distintos, son raíces del polinomio y son los valores propios de A .

Como ejemplo breve, que se describe con más detalle en la sección de ejemplos más adelante, considere la matriz $${\displaystyle A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.}$$

Tomando el determinante de ( A − λI ) , el polinomio característico de A es $${\displaystyle \det(A-\lambda I)={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}=3-4\lambda +\lambda ^{2}.}$$

Si se iguala a cero el polinomio característico, éste tiene raíces en λ=1 y λ=3 , que son los dos valores propios de A. Los vectores propios correspondientes a cada valor propio se pueden encontrar resolviendo los componentes de v en la ecuación . En este ejemplo, los vectores propios son cualquier múltiplo escalar distinto de cero de ${\displaystyle \left(A-\lambda I\right)\mathbf {v} =\mathbf {0} }$ $${\displaystyle \mathbf {v} _{\lambda =1}={\begin{bmatrix}1\\-1\end{bmatrix}},\quad \mathbf {v} _{\lambda =3}={\begin{bmatrix}1\\1\end{bmatrix}}.}$$

Si las entradas de la matriz A son todas números reales, entonces los coeficientes del polinomio característico también serán números reales, pero los valores propios pueden tener partes imaginarias distintas de cero. Por lo tanto, las entradas de los vectores propios correspondientes también pueden tener partes imaginarias distintas de cero. De manera similar, los valores propios pueden ser números irracionales incluso si todas las entradas de A son números racionales o incluso si son todos números enteros. Sin embargo, si las entradas de A son todas números algebraicos , que incluyen los racionales, los valores propios también deben ser números algebraicos.

Las raíces no reales de un polinomio real con coeficientes reales se pueden agrupar en pares de conjugados complejos , es decir, con los dos miembros de cada par que tienen partes imaginarias que difieren solo en el signo y la misma parte real. Si el grado es impar, entonces, por el teorema del valor intermedio, al menos una de las raíces es real. Por lo tanto, cualquier matriz real con orden impar tiene al menos un valor propio real, mientras que una matriz real con orden par puede no tener ningún valor propio real. Los vectores propios asociados con estos valores propios complejos también son complejos y también aparecen en pares conjugados complejos.

Espectro de una matriz

El espectro de una matriz es la lista de valores propios, repetidos según su multiplicidad; en una notación alternativa, el conjunto de valores propios con sus multiplicidades.

Una cantidad importante asociada con el espectro es el valor absoluto máximo de cualquier valor propio, conocido como radio espectral de la matriz.

Multiplicidad algebraica

Sea λ _i un valor propio de una matriz A de n por n . La multiplicidad algebraica μ _A ( λ _i ) del valor propio es su multiplicidad como raíz del polinomio característico, es decir, el entero más grande k tal que ( λ − λ _i ) ^k divide exactamente ese polinomio. ^{[9] [25] [26]}

Supóngase que una matriz A tiene dimensión n y d ≤ n valores propios distintos. Mientras que la ecuación ( 4 ) factoriza el polinomio característico de A en el producto de n términos lineales con algunos términos que potencialmente se repiten, el polinomio característico también puede escribirse como el producto de d términos, cada uno correspondiente a un valor propio distinto y elevado a la potencia de la multiplicidad algebraica, $${\displaystyle \det(A-\lambda I)=(\lambda _{1}-\lambda )^{\mu _{A}(\lambda _{1})}(\lambda _{2}-\lambda )^{\mu _{A}(\lambda _{2})}\cdots (\lambda _{d}-\lambda )^{\mu _{A}(\lambda _{d})}.}$$

Si d = n entonces el lado derecho es el producto de n términos lineales y esto es lo mismo que la ecuación ( 4 ). El tamaño de la multiplicidad algebraica de cada valor propio está relacionado con la dimensión n como $${\displaystyle {\begin{aligned}1&\leq \mu _{A}(\lambda _{i})\leq n,\\\mu _{A}&=\sum _{i=1}^{d}\mu _{A}\left(\lambda _{i}\right)=n.\end{aligned}}}$$

Si μ _A ( λ _i ) = 1, entonces se dice que λ _i es un valor propio simple . ^[26] Si μ _A ( λ _i ) es igual a la multiplicidad geométrica de λ _i , γ _A ( λ _i ), definida en la siguiente sección, entonces se dice que λ _i es un valor propio semisimple .

Espacios propios, multiplicidad geométrica y base propia para matrices

Dado un valor propio particular λ de la matriz A de n por n , defina el conjunto E como todos los vectores v que satisfacen la ecuación ( 2 ), $${\displaystyle E=\left\{\mathbf {v} :\left(A-\lambda I\right)\mathbf {v} =\mathbf {0} \right\}.}$$

Por un lado, este conjunto es precisamente el núcleo o espacio nulo de la matriz ( A − λI ). Por otro lado, por definición, cualquier vector distinto de cero que satisfaga esta condición es un vector propio de A asociado a λ . Así, el conjunto E es la unión del vector cero con el conjunto de todos los vectores propios de A asociados a λ , y E es igual al espacio nulo de ( A − λI ). E se denomina espacio propio o espacio característico de A asociado a λ . ^{[27] [9]} En general λ es un número complejo y los vectores propios son matrices complejas n por 1. Una propiedad del espacio nulo es que es un subespacio lineal , por lo que E es un subespacio lineal de . ${\displaystyle \mathbb {C} ^{n}}$

Como el espacio propio E es un subespacio lineal, es cerrado bajo la adición. Es decir, si dos vectores u y v pertenecen al conjunto E , escrito u , v ∈ E , entonces ( u + v ) ∈ E o equivalentemente A ( u + v ) = λ ( u + v ) . Esto se puede comprobar utilizando la propiedad distributiva de la multiplicación de matrices. De manera similar, como E es un subespacio lineal, es cerrado bajo la multiplicación escalar. Es decir, si v ∈ E y α es un número complejo, ( α v ) ∈ E o equivalentemente A ( α v ) = λ ( α v ) . Esto se puede comprobar observando que la multiplicación de matrices complejas por números complejos es conmutativa . Siempre que u + v y α v no sean cero, también son vectores propios de A asociados con λ .

La dimensión del espacio propio E asociado con λ , o equivalentemente el número máximo de vectores propios linealmente independientes asociados con λ , se denomina multiplicidad geométrica del valor propio . Debido a que E también es el espacio nulo de ( A − λI ), la multiplicidad geométrica de λ es la dimensión del espacio nulo de ( A − λI ), también llamada nulidad de ( A − λI ), que se relaciona con la dimensión y el rango de ( A − λI ) como ${\displaystyle \gamma _{A}(\lambda )}$ $${\displaystyle \gamma _{A}(\lambda )=n-\operatorname {rank} (A-\lambda I).}$$

Debido a la definición de valores propios y vectores propios, la multiplicidad geométrica de un valor propio debe ser al menos uno, es decir, cada valor propio tiene al menos un vector propio asociado. Además, la multiplicidad geométrica de un valor propio no puede superar su multiplicidad algebraica. Además, recuerde que la multiplicidad algebraica de un valor propio no puede superar n . $${\displaystyle 1\leq \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )\leq n}$$

Para demostrar la desigualdad , considere cómo la definición de multiplicidad geométrica implica la existencia de vectores propios ortonormales , tales que . Por lo tanto, podemos encontrar una matriz (unitaria) cuyas primeras columnas son estos vectores propios, y cuyas columnas restantes pueden ser cualquier conjunto ortonormal de vectores ortogonales a estos vectores propios de . Entonces tiene rango completo y, por lo tanto, es invertible. Evaluando , obtenemos una matriz cuyo bloque superior izquierdo es la matriz diagonal . Esto se puede ver evaluando lo que el lado izquierdo hace con los vectores base de la primera columna. Al reorganizar y agregar en ambos lados, obtenemos ya que conmuta con . En otras palabras, es similar a , y . Pero a partir de la definición de , sabemos que contiene un factor , lo que significa que la multiplicidad algebraica de debe satisfacer . ${\displaystyle \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )}$ ${\displaystyle \gamma _{A}(\lambda )}$ ${\displaystyle {\boldsymbol {v}}_{1},\,\ldots ,\,{\boldsymbol {v}}_{\gamma _{A}(\lambda )}}$ ${\displaystyle A{\boldsymbol {v}}_{k}=\lambda {\boldsymbol {v}}_{k}}$ ${\displaystyle V}$ ${\displaystyle \gamma _{A}(\lambda )}$ ${\displaystyle n-\gamma _{A}(\lambda )}$ ${\displaystyle A}$ ${\displaystyle V}$ ${\displaystyle D:=V^{T}AV}$ ${\displaystyle \lambda I_{\gamma _{A}(\lambda )}}$ ${\displaystyle -\xi V}$ ${\displaystyle (A-\xi I)V=V(D-\xi I)}$ ${\displaystyle I}$ ${\displaystyle V}$ ${\displaystyle A-\xi I}$ ${\displaystyle D-\xi I}$ ${\displaystyle \det(A-\xi I)=\det(D-\xi I)}$ ${\displaystyle D}$ ${\displaystyle \det(D-\xi I)}$ ${\displaystyle (\xi -\lambda )^{\gamma _{A}(\lambda )}}$ ${\displaystyle \lambda }$ ${\displaystyle \mu _{A}(\lambda )\geq \gamma _{A}(\lambda )}$

Supongamos que tiene valores propios distintos , donde la multiplicidad geométrica de es . La multiplicidad geométrica total de , es la dimensión de la suma de todos los espacios propios de los valores propios de , o equivalentemente el número máximo de vectores propios linealmente independientes de . Si , entonces ${\displaystyle A}$ ${\displaystyle d\leq n}$ ${\displaystyle \lambda _{1},\ldots ,\lambda _{d}}$ ${\displaystyle \lambda _{i}}$ ${\displaystyle \gamma _{A}(\lambda _{i})}$ ${\displaystyle A}$ $${\displaystyle {\begin{aligned}\gamma _{A}&=\sum _{i=1}^{d}\gamma _{A}(\lambda _{i}),\\d&\leq \gamma _{A}\leq n,\end{aligned}}}$$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \gamma _{A}=n}$

• La suma directa de los espacios propios de todos los valores propios de es el espacio vectorial completo . ${\displaystyle A}$ ${\displaystyle \mathbb {C} ^{n}}$
• Una base de se puede formar a partir de vectores propios linealmente independientes de ; dicha base se denomina base propia ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle n}$ ${\displaystyle A}$
• Cualquier vector en puede escribirse como una combinación lineal de vectores propios de . ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle A}$

Propiedades adicionales

Sea una matriz arbitraria de números complejos con valores propios . Cada valor propio aparece veces en esta lista, donde es la multiplicidad algebraica del valor propio. Las siguientes son propiedades de esta matriz y sus valores propios: ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ ${\displaystyle \mu _{A}(\lambda _{i})}$ ${\displaystyle \mu _{A}(\lambda _{i})}$

• La traza de , definida como la suma de sus elementos diagonales, es también la suma de todos los valores propios, ^{[28] [29] [30]} ${\displaystyle A}$

  ${\displaystyle \operatorname {tr} (A)=\sum _{i=1}^{n}a_{ii}=\sum _{i=1}^{n}\lambda _{i}=\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}.}$

• El determinante de es el producto de todos sus valores propios, ^{[28] [31] [32]} ${\displaystyle A}$

  ${\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

• Los valores propios de la ésima potencia de ; es decir, los valores propios de , para cualquier entero positivo , son . ${\displaystyle k}$ ${\displaystyle A}$ ${\displaystyle A^{k}}$ ${\displaystyle k}$ ${\displaystyle \lambda _{1}^{k},\ldots ,\lambda _{n}^{k}}$
• La matriz es invertible si y sólo si cada valor propio es distinto de cero. ${\displaystyle A}$
• Si es invertible, entonces los valores propios de son y la multiplicidad geométrica de cada valor propio coincide. Además, dado que el polinomio característico del inverso es el polinomio recíproco del original, los valores propios comparten la misma multiplicidad algebraica. ${\displaystyle A}$ ${\displaystyle A^{-1}}$ ${\textstyle {\frac {1}{\lambda _{1}}},\ldots ,{\frac {1}{\lambda _{n}}}}$
• Si es igual a su transpuesta conjugada o, equivalentemente, si es hermítica , entonces todo valor propio es real. Lo mismo se aplica a cualquier matriz real simétrica . ${\displaystyle A}$ ${\displaystyle A^{*}}$ ${\displaystyle A}$
• Si no es solo hermítico sino también positivo-definido , positivo-semidefinido, negativo-definido o negativo-semidefinido, entonces cada valor propio es positivo, no negativo, negativo o no positivo, respectivamente. ${\displaystyle A}$
• Si es unitario , cada valor propio tiene valor absoluto . ${\displaystyle A}$ ${\displaystyle |\lambda _{i}|=1}$
• Si es una matriz y son sus valores propios, entonces los valores propios de la matriz (donde es la matriz identidad) son . Además, si , los valores propios de son . De manera más general, para un polinomio los valores propios de la matriz son . ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle \{\lambda _{1},\ldots ,\lambda _{k}\}}$ ${\displaystyle I+A}$ ${\displaystyle I}$ ${\displaystyle \{\lambda _{1}+1,\ldots ,\lambda _{k}+1\}}$ ${\displaystyle \alpha \in \mathbb {C} }$ ${\displaystyle \alpha I+A}$ ${\displaystyle \{\lambda _{1}+\alpha ,\ldots ,\lambda _{k}+\alpha \}}$ ${\displaystyle P}$ ${\displaystyle P(A)}$ ${\displaystyle \{P(\lambda _{1}),\ldots ,P(\lambda _{k})\}}$

Vectores propios izquierdo y derecho

Muchas disciplinas tradicionalmente representan los vectores como matrices con una sola columna en lugar de matrices con una sola fila. Por esa razón, la palabra "vector propio" en el contexto de matrices casi siempre se refiere a un vector propio derecho , es decir, un vector columna que multiplica por la derecha la matriz en la ecuación definitoria, ecuación ( 1 ). ${\displaystyle n\times n}$ ${\displaystyle A}$ $${\displaystyle A\mathbf {v} =\lambda \mathbf {v} .}$$

El problema de los valores propios y los vectores propios también se puede definir para vectores fila que multiplican por la izquierda la matriz . En esta formulación, la ecuación definitoria es ${\displaystyle A}$ $${\displaystyle \mathbf {u} A=\kappa \mathbf {u} ,}$$

donde es un escalar y es una matriz. Cualquier vector fila que satisfaga esta ecuación se denomina vector propio izquierdo de y es su valor propio asociado. Tomando la transpuesta de esta ecuación, ${\displaystyle \kappa }$ ${\displaystyle u}$ ${\displaystyle 1\times n}$ ${\displaystyle u}$ ${\displaystyle A}$ ${\displaystyle \kappa }$ $${\displaystyle A^{\textsf {T}}\mathbf {u} ^{\textsf {T}}=\kappa \mathbf {u} ^{\textsf {T}}.}$$

Comparando esta ecuación con la ecuación ( 1 ), se sigue inmediatamente que un vector propio izquierdo de es el mismo que la transpuesta de un vector propio derecho de , con el mismo valor propio. Además, dado que el polinomio característico de es el mismo que el polinomio característico de , los vectores propios izquierdo y derecho de están asociados con los mismos valores propios. ${\displaystyle A}$ ${\displaystyle A^{\textsf {T}}}$ ${\displaystyle A^{\textsf {T}}}$ ${\displaystyle A}$ ${\displaystyle A}$

Diagonalización y descomposición propia

Supóngase que los vectores propios de A forman una base, o equivalentemente, A tiene n vectores propios linealmente independientes v ₁ , v ₂ , ..., v _n con valores propios asociados λ ₁ , λ ₂ , ..., λ _n . Los valores propios no necesitan ser distintos. Defina una matriz cuadrada Q cuyas columnas sean los n vectores propios linealmente independientes de A ,

${\displaystyle Q={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}.}$

Dado que cada columna de Q es un vector propio de A , al multiplicar A por Q hacia la derecha se escala cada columna de Q por su valor propio asociado,

${\displaystyle AQ={\begin{bmatrix}\lambda _{1}\mathbf {v} _{1}&\lambda _{2}\mathbf {v} _{2}&\cdots &\lambda _{n}\mathbf {v} _{n}\end{bmatrix}}.}$

Con esto en mente, defina una matriz diagonal Λ donde cada elemento diagonal Λ _ii es el valor propio asociado con la i- ésima columna de Q . Luego

${\displaystyle AQ=Q\Lambda .}$

Como las columnas de Q son linealmente independientes, Q es invertible. Multiplicando ambos lados de la ecuación por Q ⁻¹ ,

${\displaystyle A=Q\Lambda Q^{-1},}$

o en su lugar, multiplicando hacia la izquierda ambos lados por Q ⁻¹ ,

${\displaystyle Q^{-1}AQ=\Lambda .}$

Por lo tanto, A se puede descomponer en una matriz compuesta por sus vectores propios, una matriz diagonal con sus valores propios a lo largo de la diagonal y la inversa de la matriz de vectores propios. Esto se llama descomposición propia y es una transformación de similitud . Se dice que una matriz A de este tipo es similar a la matriz diagonal Λ o diagonalizable . La matriz Q es la matriz de cambio de base de la transformación de similitud. Esencialmente, las matrices A y Λ representan la misma transformación lineal expresada en dos bases diferentes. Los vectores propios se utilizan como base cuando se representa la transformación lineal como Λ.

Por el contrario, supongamos que una matriz A es diagonalizable. Sea P una matriz cuadrada no singular tal que P ⁻¹ AP es una matriz diagonal D . Multiplicando ambas por P , AP = PD . Por lo tanto, cada columna de P debe ser un vector propio de A cuyo valor propio sea el elemento diagonal correspondiente de D . Como las columnas de P deben ser linealmente independientes para que P sea invertible, existen n vectores propios linealmente independientes de A . Entonces se deduce que los vectores propios de A forman una base si y solo si A es diagonalizable.

Una matriz que no es diagonalizable se dice que es defectuosa . Para matrices defectuosas, la noción de vectores propios se generaliza a vectores propios generalizados y la matriz diagonal de valores propios se generaliza a la forma normal de Jordan . Sobre un cuerpo algebraicamente cerrado, cualquier matriz A tiene una forma normal de Jordan y, por lo tanto, admite una base de vectores propios generalizados y una descomposición en espacios propios generalizados .

Caracterización variacional

En el caso hermítico , los valores propios pueden tener una caracterización variacional. El valor propio más grande de es el valor máximo de la forma cuadrática . Un valor de que realiza ese máximo es un vector propio. ${\displaystyle H}$ ${\displaystyle \mathbf {x} ^{\textsf {T}}H\mathbf {x} /\mathbf {x} ^{\textsf {T}}\mathbf {x} }$ ${\displaystyle \mathbf {x} }$

Ejemplos de matrices

Ejemplo de matriz bidimensional

La matriz de transformación A = conserva la dirección de los vectores violeta paralelos a v _{λ =1} = [1 −1] ^T y los vectores azules paralelos a v _{λ =3} = [1 1] ^T . Los vectores rojos no son paralelos a ninguno de los vectores propios, por lo que sus direcciones cambian por la transformación. Las longitudes de los vectores violeta no cambian después de la transformación (debido a su valor propio de 1), mientras que los vectores azules tienen tres veces la longitud del original (debido a su valor propio de 3). Véase también: Una versión extendida, que muestra los cuatro cuadrantes . ${\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}$

Considere la matriz $${\displaystyle A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.}$$

La figura de la derecha muestra el efecto de esta transformación sobre las coordenadas de los puntos en el plano. Los vectores propios v de esta transformación satisfacen la ecuación ( 1 ), y los valores de λ para los cuales el determinante de la matriz ( A  −  λI ) es igual a cero son los valores propios.

Tomando el determinante para encontrar el polinomio característico de A , $${\displaystyle {\begin{aligned}\det(A-\lambda I)&=\left|{\begin{bmatrix}2&1\\1&2\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}\\[6pt]&=3-4\lambda +\lambda ^{2}\\[6pt]&=(\lambda -3)(\lambda -1).\end{aligned}}}$$

Al establecer el polinomio característico igual a cero, tiene raíces en λ = 1 y λ = 3 , que son los dos valores propios de A.

Para λ = 1 , la ecuación ( 2 ) se convierte en, $${\displaystyle (A-I)\mathbf {v} _{\lambda =1}={\begin{bmatrix}1&1\\1&1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}}$$ $${\displaystyle 1v_{1}+1v_{2}=0}$$

Cualquier vector distinto de cero con v ₁ = − v ₂ resuelve esta ecuación. Por lo tanto, es un vector propio de A correspondiente a λ = 1, al igual que cualquier múltiplo escalar de este vector. $${\displaystyle \mathbf {v} _{\lambda =1}={\begin{bmatrix}v_{1}\\-v_{1}\end{bmatrix}}={\begin{bmatrix}1\\-1\end{bmatrix}}}$$

Para λ = 3 , la ecuación ( 2 ) se convierte en $${\displaystyle {\begin{aligned}(A-3I)\mathbf {v} _{\lambda =3}&={\begin{bmatrix}-1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\\-1v_{1}+1v_{2}&=0;\\1v_{1}-1v_{2}&=0\end{aligned}}}$$

Cualquier vector distinto de cero con v ₁ = v ₂ resuelve esta ecuación. Por lo tanto, $${\displaystyle \mathbf {v} _{\lambda =3}={\begin{bmatrix}v_{1}\\v_{1}\end{bmatrix}}={\begin{bmatrix}1\\1\end{bmatrix}}}$$

es un vector propio de A correspondiente a λ = 3, como lo es cualquier múltiplo escalar de este vector.

Por lo tanto, los vectores v _{λ = 1} y v _{λ = 3} son vectores propios de A asociados a los valores propios λ = 1 y λ = 3 , respectivamente.

Ejemplo de matriz tridimensional

Considere la matriz $${\displaystyle A={\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}.}$$

El polinomio característico de A es $${\displaystyle {\begin{aligned}\det(A-\lambda I)&=\left|{\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}-\lambda {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &0&0\\0&3-\lambda &4\\0&4&9-\lambda \end{vmatrix}},\\[6pt]&=(2-\lambda ){\bigl [}(3-\lambda )(9-\lambda )-16{\bigr ]}=-\lambda ^{3}+14\lambda ^{2}-35\lambda +22.\end{aligned}}}$$

Las raíces del polinomio característico son 2, 1 y 11, que son los únicos tres valores propios de A. Estos valores propios corresponden a los vectores propios , , y , o cualquier múltiplo distinto de cero de los mismos. ${\displaystyle {\begin{bmatrix}1&0&0\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&-2&1\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&1&2\end{bmatrix}}^{\textsf {T}}}$

Ejemplo de matriz tridimensional con valores propios complejos

Considere la matriz de permutación cíclica $${\displaystyle A={\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}}.}$$

Esta matriz desplaza las coordenadas del vector una posición hacia arriba y desplaza la primera coordenada hacia abajo. Su polinomio característico es 1 −  λ ³ , cuyas raíces son donde es una unidad imaginaria con . $${\displaystyle {\begin{aligned}\lambda _{1}&=1\\\lambda _{2}&=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\lambda _{3}&=\lambda _{2}^{*}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{aligned}}}$$ ${\displaystyle i}$ ${\displaystyle i^{2}=-1}$

Para el valor propio real λ ₁ = 1, cualquier vector con tres entradas iguales distintas de cero es un vector propio. Por ejemplo, $${\displaystyle A{\begin{bmatrix}5\\5\\5\end{bmatrix}}={\begin{bmatrix}5\\5\\5\end{bmatrix}}=1\cdot {\begin{bmatrix}5\\5\\5\end{bmatrix}}.}$$

Para el par conjugado complejo de valores propios imaginarios, $${\displaystyle \lambda _{2}\lambda _{3}=1,\quad \lambda _{2}^{2}=\lambda _{3},\quad \lambda _{3}^{2}=\lambda _{2}.}$$

Entonces y $${\displaystyle A{\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}}={\begin{bmatrix}\lambda _{2}\\\lambda _{3}\\1\end{bmatrix}}=\lambda _{2}\cdot {\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}},}$$ $${\displaystyle A{\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}={\begin{bmatrix}\lambda _{3}\\\lambda _{2}\\1\end{bmatrix}}=\lambda _{3}\cdot {\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}.}$$

Por lo tanto, los otros dos vectores propios de A son complejos y son y con valores propios λ ₂ y λ ₃ , respectivamente. Los dos vectores propios complejos también aparecen en un par conjugado complejo, ${\displaystyle \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}1&\lambda _{2}&\lambda _{3}\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}1&\lambda _{3}&\lambda _{2}\end{bmatrix}}^{\textsf {T}}}$ $${\displaystyle \mathbf {v} _{\lambda _{2}}=\mathbf {v} _{\lambda _{3}}^{*}.}$$

Ejemplo de matriz diagonal

Las matrices con entradas solo a lo largo de la diagonal principal se denominan matrices diagonales . Los valores propios de una matriz diagonal son los propios elementos diagonales. Considere la matriz $${\displaystyle A={\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\end{bmatrix}}.}$$

El polinomio característico de A es $${\displaystyle \det(A-\lambda I)=(1-\lambda )(2-\lambda )(3-\lambda ),}$$

que tiene las raíces λ ₁ = 1 , λ ₂ = 2 y λ ₃ = 3 . Estas raíces son los elementos diagonales así como los valores propios de  A .

Cada elemento diagonal corresponde a un vector propio cuyo único componente distinto de cero se encuentra en la misma fila que ese elemento diagonal. En el ejemplo, los valores propios corresponden a los vectores propios, $${\displaystyle \mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\0\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},}$$

respectivamente, así como múltiplos escalares de estos vectores.

Ejemplo de matriz triangular

Una matriz cuyos elementos por encima de la diagonal principal son todos cero se denomina matriz triangular inferior , mientras que una matriz cuyos elementos por debajo de la diagonal principal son todos cero se denomina matriz triangular superior . Al igual que con las matrices diagonales, los valores propios de las matrices triangulares son los elementos de la diagonal principal.

Consideremos la matriz triangular inferior, $${\displaystyle A={\begin{bmatrix}1&0&0\\1&2&0\\2&3&3\end{bmatrix}}.}$$

El polinomio característico de A es $${\displaystyle \det(A-\lambda I)=(1-\lambda )(2-\lambda )(3-\lambda ),}$$

que tiene las raíces λ ₁ = 1 , λ ₂ = 2 y λ ₃ = 3 . Estas raíces son los elementos diagonales así como los valores propios de  A .

Estos valores propios corresponden a los vectores propios, $${\displaystyle \mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\-1\\{\frac {1}{2}}\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\-3\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},}$$

respectivamente, así como múltiplos escalares de estos vectores.

Ejemplo de matriz con valores propios repetidos

Como en el ejemplo anterior, la matriz triangular inferior tiene un polinomio característico que es el producto de sus elementos diagonales, $${\displaystyle A={\begin{bmatrix}2&0&0&0\\1&2&0&0\\0&1&3&0\\0&0&1&3\end{bmatrix}},}$$ $${\displaystyle \det(A-\lambda I)={\begin{vmatrix}2-\lambda &0&0&0\\1&2-\lambda &0&0\\0&1&3-\lambda &0\\0&0&1&3-\lambda \end{vmatrix}}=(2-\lambda )^{2}(3-\lambda )^{2}.}$$

Las raíces de este polinomio, y por tanto los valores propios, son 2 y 3. La multiplicidad algebraica de cada valor propio es 2; en otras palabras, ambos son raíces dobles. La suma de las multiplicidades algebraicas de todos los valores propios distintos es μ _A = 4 = n , el orden del polinomio característico y la dimensión de A .

Por otra parte, la multiplicidad geométrica del valor propio 2 es solo 1, porque su espacio propio está abarcado por un solo vector y, por lo tanto, es unidimensional. De manera similar, la multiplicidad geométrica del valor propio 3 es 1 porque su espacio propio está abarcado por un solo vector . La multiplicidad geométrica total γ _A es 2, que es la más pequeña que podría ser para una matriz con dos valores propios distintos. Las multiplicidades geométricas se definen en una sección posterior. ${\displaystyle {\begin{bmatrix}0&1&-1&1\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&0&0&1\end{bmatrix}}^{\textsf {T}}}$

Identidad vector propio-valor propio

Para una matriz hermítica , la norma al cuadrado del componente j de un vector propio normalizado se puede calcular utilizando solo los valores propios de la matriz y los valores propios de la matriz menor correspondiente , donde es la submatriz formada al eliminar la fila y columna j de la matriz original. ^{[33] [34] [35]} Esta identidad también se extiende a matrices diagonalizables y ha sido redescubierta muchas veces en la literatura. ^{[34] [36]} $${\displaystyle |v_{i,j}|^{2}={\frac {\prod _{k}{(\lambda _{i}-\lambda _{k}(M_{j}))}}{\prod _{k\neq i}{(\lambda _{i}-\lambda _{k})}}},}$$ ${\textstyle M_{j}}$

Valores propios y funciones propias de operadores diferenciales

Las definiciones de valor propio y vectores propios de una transformación lineal T siguen siendo válidas incluso si el espacio vectorial subyacente es un espacio de Hilbert o de Banach de dimensión infinita. Una clase ampliamente utilizada de transformaciones lineales que actúan en espacios de dimensión infinita son los operadores diferenciales en espacios de funciones . Sea D un operador diferencial lineal en el espacio C ^∞ de funciones reales infinitamente diferenciables de un argumento real t . La ecuación del valor propio para D es la ecuación diferencial $${\displaystyle Df(t)=\lambda f(t)}$$

Las funciones que satisfacen esta ecuación son vectores propios de D y se denominan comúnmente funciones propias .

Ejemplo de operador derivado

Considere el operador derivado con ecuación de valor propio ${\displaystyle {\tfrac {d}{dt}}}$ $${\displaystyle {\frac {d}{dt}}f(t)=\lambda f(t).}$$

Esta ecuación diferencial se puede resolver multiplicando ambos lados por dt / f ( t ) e integrando . Su solución, la función exponencial, es la función propia del operador derivada. En este caso, la función propia es en sí misma una función de su valor propio asociado. En particular, para λ = 0, la función propia f ( t ) es una constante. $${\displaystyle f(t)=f(0)e^{\lambda t},}$$

El artículo principal sobre funciones propias ofrece otros ejemplos.

Definición general

El concepto de valores propios y vectores propios se extiende naturalmente a transformaciones lineales arbitrarias sobre espacios vectoriales arbitrarios. Sea V cualquier espacio vectorial sobre un cuerpo K de escalares y sea T una transformación lineal que aplica V a V , $${\displaystyle T:V\to V.}$$

Decimos que un vector distinto de cero v ∈ V es un vector propio de T si y solo si existe un escalar λ ∈ K tal que

Esta ecuación se denomina ecuación de valor propio para T , y el escalar λ es el valor propio de T correspondiente al vector propio v . T ( v ) es el resultado de aplicar la transformación T al vector v , mientras que λ v es el producto del escalar λ con v . ^{[37] [38]}

Espacios propios, multiplicidad geométrica y base propia

Dado un valor propio λ , considere el conjunto $${\displaystyle E=\left\{\mathbf {v} :T(\mathbf {v} )=\lambda \mathbf {v} \right\},}$$

que es la unión del vector cero con el conjunto de todos los vectores propios asociados a  λ . E se denomina espacio propio o espacio característico de T asociado a  λ . ^[39]

Por definición de una transformación lineal, $${\displaystyle {\begin{aligned}T(\mathbf {x} +\mathbf {y} )&=T(\mathbf {x} )+T(\mathbf {y} ),\\T(\alpha \mathbf {x} )&=\alpha T(\mathbf {x} ),\end{aligned}}}$$

para x ,  y  ∈ V y α  ∈ K . Por lo tanto, si u y v son vectores propios de T asociados con el valor propio λ , es decir u ,  v  ∈ E , entonces $${\displaystyle {\begin{aligned}T(\mathbf {u} +\mathbf {v} )&=\lambda (\mathbf {u} +\mathbf {v} ),\\T(\alpha \mathbf {v} )&=\lambda (\alpha \mathbf {v} ).\end{aligned}}}$$

Por lo tanto, tanto u + v como α v son cero o vectores propios de T asociados con λ , es decir, u + v , α v ∈ E , y E está cerrado bajo la adición y la multiplicación escalar. El espacio propio E asociado con λ es, por lo tanto, un subespacio lineal de V . ^[40] Si ese subespacio tiene dimensión 1, a veces se lo denomina línea propia . ^[41]

La multiplicidad geométrica γ _T ( λ ) de un valor propio λ es la dimensión del espacio propio asociado con λ , es decir, el número máximo de vectores propios linealmente independientes asociados con ese valor propio. ^{[9] [26] [42]} Por la definición de valores propios y vectores propios, γ _T ( λ ) ≥ 1 porque cada valor propio tiene al menos un vector propio.

Los espacios propios de T siempre forman una suma directa . En consecuencia, los vectores propios de distintos valores propios son siempre linealmente independientes. Por lo tanto, la suma de las dimensiones de los espacios propios no puede superar la dimensión n del espacio vectorial en el que opera T , y no puede haber más de n valores propios distintos. ^[d]

Cualquier subespacio abarcado por vectores propios de T es un subespacio invariante de T , y la restricción de T a dicho subespacio es diagonalizable. Además, si todo el espacio vectorial V puede ser abarcado por los vectores propios de T , o equivalentemente si la suma directa de los espacios propios asociados con todos los valores propios de T es todo el espacio vectorial V , entonces una base de V llamada base propia puede formarse a partir de vectores propios linealmente independientes de T . Cuando T admite una base propia, T es diagonalizable.

Teoría espectral

Si λ es un valor propio de T , entonces el operador ( T − λI ) no es biunívoco y, por lo tanto, su inverso ( T − λI ) ⁻¹ no existe. Lo contrario es cierto para espacios vectoriales de dimensión finita, pero no para espacios vectoriales de dimensión infinita. En general, el operador ( T − λI ) puede no tener inverso incluso si λ no es un valor propio.

Por esta razón, en el análisis funcional los valores propios se pueden generalizar al espectro de un operador lineal T como el conjunto de todos los escalares λ para los cuales el operador ( T − λI ) no tiene inverso acotado . El espectro de un operador siempre contiene todos sus valores propios pero no está limitado a ellos.

Álgebras asociativas y teoría de la representación

Se puede generalizar el objeto algebraico que actúa sobre el espacio vectorial, reemplazando un único operador que actúa sobre un espacio vectorial por una representación algebraica : un álgebra asociativa que actúa sobre un módulo . El estudio de tales acciones es el campo de la teoría de la representación .

El concepto teórico de representación de peso es un análogo de los valores propios, mientras que los vectores de peso y los espacios de peso son los análogos de los vectores propios y los espacios propios, respectivamente.

El haz propio de Hecke es un tensor múltiplo de sí mismo y se considera en la correspondencia de Langlands .

Ecuaciones dinámicas

Las ecuaciones diferenciales más simples tienen la forma

${\displaystyle x_{t}=a_{1}x_{t-1}+a_{2}x_{t-2}+\cdots +a_{k}x_{t-k}.}$

La solución de esta ecuación para x en términos de t se encuentra utilizando su ecuación característica

${\displaystyle \lambda ^{k}-a_{1}\lambda ^{k-1}-a_{2}\lambda ^{k-2}-\cdots -a_{k-1}\lambda -a_{k}=0,}$

que se puede encontrar apilando en forma matricial un conjunto de ecuaciones que consisten en la ecuación diferencial anterior y las ecuaciones k  – 1 que dan un sistema k -dimensional de primer orden en el vector de variable apilada en términos de su valor una vez rezagado, y tomando la ecuación característica de la matriz de este sistema. Esta ecuación da k raíces características para usar en la ecuación de solución ${\displaystyle x_{t-1}=x_{t-1},\ \dots ,\ x_{t-k+1}=x_{t-k+1},}$ ${\displaystyle {\begin{bmatrix}x_{t}&\cdots &x_{t-k+1}\end{bmatrix}}}$ ${\displaystyle \lambda _{1},\,\ldots ,\,\lambda _{k},}$

${\displaystyle x_{t}=c_{1}\lambda _{1}^{t}+\cdots +c_{k}\lambda _{k}^{t}.}$

Se utiliza un procedimiento similar para resolver una ecuación diferencial de la forma

${\displaystyle {\frac {d^{k}x}{dt^{k}}}+a_{k-1}{\frac {d^{k-1}x}{dt^{k-1}}}+\cdots +a_{1}{\frac {dx}{dt}}+a_{0}x=0.}$

Cálculo

El cálculo de valores propios y vectores propios es un tema en el que la teoría, tal como se presenta en los libros de texto de álgebra lineal elemental, a menudo está muy lejos de la práctica.

Método clásico

El método clásico consiste en encontrar primero los valores propios y luego calcular los vectores propios para cada valor propio. En varios aspectos, no es adecuado para operaciones aritméticas no exactas, como la de punto flotante .

Valores propios

Los valores propios de una matriz se pueden determinar hallando las raíces del polinomio característico. Esto es fácil en el caso de las matrices, pero la dificultad aumenta rápidamente con el tamaño de la matriz. ${\displaystyle A}$ ${\displaystyle 2\times 2}$

En teoría, los coeficientes del polinomio característico se pueden calcular con exactitud, ya que son sumas de productos de elementos de la matriz; y hay algoritmos que pueden encontrar todas las raíces de un polinomio de grado arbitrario con cualquier precisión requerida . ^[43] Sin embargo, este enfoque no es viable en la práctica porque los coeficientes estarían contaminados por errores de redondeo inevitables , y las raíces de un polinomio pueden ser una función extremadamente sensible de los coeficientes (como lo ejemplifica el polinomio de Wilkinson ). ^[43] Incluso para matrices cuyos elementos son números enteros, el cálculo se vuelve no trivial, porque las sumas son muy largas; el término constante es el determinante , que para una matriz es una suma de diferentes productos. ^[e] ${\displaystyle n\times n}$ ${\displaystyle n!}$

Las fórmulas algebraicas explícitas para las raíces de un polinomio solo existen si el grado es 4 o menos. Según el teorema de Abel-Ruffini, no existe una fórmula algebraica general, explícita y exacta para las raíces de un polinomio con grado 5 o más. (La generalidad importa porque cualquier polinomio con grado es el polinomio característico de alguna matriz compañera de orden ). Por lo tanto, para matrices de orden 5 o más, los valores y vectores propios no se pueden obtener mediante una fórmula algebraica explícita y, por lo tanto, deben calcularse mediante métodos numéricos aproximados . Incluso la fórmula exacta para las raíces de un polinomio de grado 3 es numéricamente impráctica. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Vectores propios

Una vez que se conoce el valor (exacto) de un valor propio, se pueden encontrar los vectores propios correspondientes hallando soluciones distintas de cero de la ecuación del valor propio, que se convierte en un sistema de ecuaciones lineales con coeficientes conocidos. Por ejemplo, una vez que se sabe que 6 es un valor propio de la matriz $${\displaystyle A={\begin{bmatrix}4&1\\6&3\end{bmatrix}}}$$

Podemos encontrar sus vectores propios resolviendo la ecuación , es decir ${\displaystyle Av=6v}$ $${\displaystyle {\begin{bmatrix}4&1\\6&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}=6\cdot {\begin{bmatrix}x\\y\end{bmatrix}}}$$

Esta ecuación matricial es equivalente a dos ecuaciones lineales que son $${\displaystyle \left\{{\begin{aligned}4x+y&=6x\\6x+3y&=6y\end{aligned}}\right.}$$          ${\displaystyle \left\{{\begin{aligned}-2x+y&=0\\6x-3y&=0\end{aligned}}\right.}$

Ambas ecuaciones se reducen a una única ecuación lineal . Por lo tanto, cualquier vector de la forma , para cualquier número real distinto de cero , es un vector propio de con valor propio . ${\displaystyle y=2x}$ ${\displaystyle {\begin{bmatrix}a&2a\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle \lambda =6}$

La matriz anterior tiene otro valor propio . Un cálculo similar muestra que los vectores propios correspondientes son las soluciones distintas de cero de , es decir, cualquier vector de la forma , para cualquier número real distinto de cero . ${\displaystyle A}$ ${\displaystyle \lambda =1}$ ${\displaystyle 3x+y=0}$ ${\displaystyle {\begin{bmatrix}b&-3b\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle b}$

Métodos iterativos simples

El enfoque inverso, de buscar primero los vectores propios y luego determinar cada valor propio a partir de su vector propio, resulta ser mucho más manejable para las computadoras. El algoritmo más fácil aquí consiste en elegir un vector inicial arbitrario y luego multiplicarlo repetidamente por la matriz (normalizando opcionalmente el vector para mantener sus elementos de tamaño razonable); esto hace que el vector converja hacia un vector propio. Una variación es, en cambio, multiplicar el vector por ; esto hace que converja hacia un vector propio del valor propio más cercano a . ${\displaystyle (A-\mu I)^{-1}}$ ${\displaystyle \mu \in \mathbb {C} }$

Si es (una buena aproximación de) un vector propio de , entonces el valor propio correspondiente se puede calcular como ${\displaystyle \mathbf {v} }$ ${\displaystyle A}$

${\displaystyle \lambda ={\frac {\mathbf {v} ^{*}A\mathbf {v} }{\mathbf {v} ^{*}\mathbf {v} }}}$

donde denota la transpuesta conjugada de . ${\displaystyle \mathbf {v} ^{*}}$ ${\displaystyle \mathbf {v} }$

Métodos modernos

No se conocían métodos eficientes y precisos para calcular valores propios y vectores propios de matrices arbitrarias hasta que se diseñó el algoritmo QR en 1961. ^[43] La combinación de la transformación de Householder con la descomposición LU da como resultado un algoritmo con mejor convergencia que el algoritmo QR. ^{[ cita requerida ]} Para matrices dispersas hermíticas grandes , el algoritmo de Lanczos es un ejemplo de un método iterativo eficiente para calcular valores propios y vectores propios, entre varias otras posibilidades. ^[43]

La mayoría de los métodos numéricos que calculan los valores propios de una matriz también determinan un conjunto de vectores propios correspondientes como subproducto del cálculo, aunque a veces los implementadores optan por descartar la información del vector propio tan pronto como ya no es necesaria.

Aplicaciones

Transformaciones geométricas

Los vectores y valores propios pueden ser útiles para comprender las transformaciones lineales de formas geométricas. La siguiente tabla presenta algunos ejemplos de transformaciones en el plano junto con sus matrices 2×2, valores propios y vectores propios.

La ecuación característica de una rotación es una ecuación cuadrática con discriminante , que es un número negativo siempre que θ no sea un múltiplo entero de 180°. Por lo tanto, excepto en estos casos especiales, los dos valores propios son números complejos, ; y todos los vectores propios tienen entradas no reales. De hecho, excepto en esos casos especiales, una rotación cambia la dirección de cada vector distinto de cero en el plano. ${\displaystyle D=-4(\sin \theta )^{2}}$ ${\displaystyle \cos \theta \pm i\sin \theta }$

Una transformación lineal que convierte un cuadrado en un rectángulo de la misma área (una función de compresión ) tiene valores propios recíprocos.

Análisis de componentes principales

PCA de la distribución gaussiana multivariada centrada en con una desviación estándar de 3 aproximadamente en la dirección y de 1 en la dirección ortogonal. Los vectores que se muestran son vectores propios unitarios de la matriz de covarianza (simétrica, semidefinida positiva) escalada por la raíz cuadrada del valor propio correspondiente. Al igual que en el caso unidimensional, se toma la raíz cuadrada porque la desviación estándar se visualiza más fácilmente que la varianza . ${\displaystyle (1,3)}$ ${\displaystyle (0.878,0.478)}$

La descomposición propia de una matriz semidefinida positiva simétrica (PSD) produce una base ortogonal de vectores propios, cada uno de los cuales tiene un valor propio no negativo. La descomposición ortogonal de una matriz PSD se utiliza en el análisis multivariante , donde las matrices de covarianza de la muestra son PSD. Esta descomposición ortogonal se denomina análisis de componentes principales (PCA) en estadística. El PCA estudia las relaciones lineales entre variables. El PCA se realiza en la matriz de covarianza o la matriz de correlación (en la que cada variable se escala para que su varianza de muestra sea igual a uno). Para la matriz de covarianza o correlación, los vectores propios corresponden a los componentes principales y los valores propios a la varianza explicada por los componentes principales. El análisis de componentes principales de la matriz de correlación proporciona una base ortogonal para el espacio de los datos observados: en esta base, los valores propios más grandes corresponden a los componentes principales que están asociados con la mayor parte de la covariabilidad entre una serie de datos observados.

El análisis de componentes principales se utiliza como un medio de reducción de dimensionalidad en el estudio de grandes conjuntos de datos , como los que se encuentran en bioinformática . En la metodología Q , los valores propios de la matriz de correlación determinan el juicio del metodólogo Q sobre la significación práctica (que difiere de la significación estadística de las pruebas de hipótesis ; cf. criterios para determinar el número de factores ). De manera más general, el análisis de componentes principales se puede utilizar como un método de análisis factorial en el modelado de ecuaciones estructurales .

Gráficos

En la teoría de grafos espectrales , un valor propio de un grafo se define como un valor propio de la matriz de adyacencia del grafo , o (cada vez más) de la matriz laplaciana del grafo debido a su operador de Laplace discreto , que es (a veces llamado el laplaciano combinatorio ) o (a veces llamado el laplaciano normalizado ), donde es una matriz diagonal con igual al grado del vértice , y en , la entrada diagonal n es . El n-ésimo vector propio principal de un grafo se define como el vector propio correspondiente al n-ésimo valor propio más grande o al n-ésimo valor propio más pequeño del laplaciano. El primer vector propio principal del grafo también se conoce simplemente como el vector propio principal. ${\displaystyle A}$ ${\displaystyle D-A}$ ${\displaystyle I-D^{-1/2}AD^{-1/2}}$ ${\displaystyle D}$ ${\displaystyle D_{ii}}$ ${\displaystyle v_{i}}$ ${\displaystyle D^{-1/2}}$ ${\displaystyle i}$ ${\textstyle 1/{\sqrt {\deg(v_{i})}}}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$

El vector propio principal se utiliza para medir la centralidad de sus vértices. Un ejemplo es el algoritmo PageRank de Google . El vector propio principal de una matriz de adyacencia modificada del gráfico de la World Wide Web proporciona los rangos de página como sus componentes. Este vector corresponde a la distribución estacionaria de la cadena de Markov representada por la matriz de adyacencia normalizada por filas; sin embargo, la matriz de adyacencia debe modificarse primero para garantizar que exista una distribución estacionaria. El segundo vector propio más pequeño se puede utilizar para dividir el gráfico en grupos, mediante agrupamiento espectral . También hay otros métodos disponibles para el agrupamiento.

Cadenas de Markov

Una cadena de Markov se representa mediante una matriz cuyas entradas son las probabilidades de transición entre estados de un sistema. En particular, las entradas no son negativas y cada fila de la matriz suma uno, que es la suma de las probabilidades de transición de un estado a otro estado del sistema. El teorema de Perron-Frobenius proporciona condiciones suficientes para que una cadena de Markov tenga un valor propio dominante único, que gobierna la convergencia del sistema a un estado estable.

Análisis de vibraciones

Forma modal de un diapasón a una frecuencia propia de 440,09 Hz

Los problemas de valores propios ocurren naturalmente en el análisis de vibraciones de estructuras mecánicas con muchos grados de libertad . Los valores propios son las frecuencias naturales (o frecuencias propias ) de vibración, y los vectores propios son las formas de estos modos vibracionales. En particular, la vibración no amortiguada está gobernada por o $${\displaystyle m{\ddot {x}}+kx=0}$$ $${\displaystyle m{\ddot {x}}=-kx}$$

Es decir, la aceleración es proporcional a la posición (es decir, esperamos que sea sinusoidal en el tiempo). ${\displaystyle x}$

En dimensiones, se convierte en una matriz de masa y una matriz de rigidez . Las soluciones admisibles son entonces una combinación lineal de soluciones al problema de valor propio generalizado donde es el valor propio y es la frecuencia angular (imaginaria). Los modos de vibración principales son diferentes de los modos de cumplimiento principales, que son los vectores propios de solo. Además, la vibración amortiguada , gobernada por conduce a un llamado problema de valor propio cuadrático . ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle k}$ $${\displaystyle kx=\omega ^{2}mx}$$ ${\displaystyle \omega ^{2}}$ ${\displaystyle \omega }$ ${\displaystyle k}$ $${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0}$$ $${\displaystyle \left(\omega ^{2}m+\omega c+k\right)x=0.}$$

Esto puede reducirse a un problema de valor propio generalizado mediante manipulación algebraica a costa de resolver un sistema más grande.

Las propiedades de ortogonalidad de los vectores propios permiten desacoplar las ecuaciones diferenciales de modo que el sistema se pueda representar como una suma lineal de los vectores propios. El problema de los valores propios de las estructuras complejas se suele resolver mediante el análisis de elementos finitos , pero la solución se generaliza de forma clara a los problemas de vibración de valor escalar.

Tensor del momento de inercia

En mecánica , los vectores propios del tensor del momento de inercia definen los ejes principales de un cuerpo rígido . El tensor del momento de inercia es una cantidad clave necesaria para determinar la rotación de un cuerpo rígido alrededor de su centro de masas .

Tensor de tensión

En mecánica de sólidos , el tensor de tensión es simétrico y, por lo tanto, se puede descomponer en un tensor diagonal con los valores propios en la diagonal y los vectores propios como base. Debido a que es diagonal, en esta orientación, el tensor de tensión no tiene componentes de corte ; los componentes que tiene son los componentes principales.

Ecuación de Schrödinger

Las funciones de onda asociadas con los estados ligados de un electrón en un átomo de hidrógeno pueden verse como los vectores propios del hamiltoniano del átomo de hidrógeno, así como del operador de momento angular . Están asociadas con valores propios interpretados como sus energías (crecientes hacia abajo: ) y momento angular (crecientes a través de: s, p, d, ...). La ilustración muestra el cuadrado del valor absoluto de las funciones de onda. Las áreas más brillantes corresponden a una mayor densidad de probabilidad para una medición de posición . El centro de cada figura es el núcleo atómico , un protón . ${\displaystyle n=1,\,2,\,3,\,\ldots }$

Un ejemplo de una ecuación de valor propio donde la transformación se representa en términos de un operador diferencial es la ecuación de Schrödinger independiente del tiempo en mecánica cuántica : ${\displaystyle T}$

${\displaystyle H\psi _{E}=E\psi _{E}\,}$

donde , el hamiltoniano , es un operador diferencial de segundo orden y , la función de onda , es una de sus funciones propias correspondiente al valor propio , interpretado como su energía . ${\displaystyle H}$ ${\displaystyle \psi _{E}}$ ${\displaystyle E}$

Sin embargo, en el caso en que uno esté interesado únicamente en las soluciones de estado límite de la ecuación de Schrödinger, se busca dentro del espacio de funciones integrables al cuadrado . Dado que este espacio es un espacio de Hilbert con un producto escalar bien definido , se puede introducir un conjunto base en el que y se pueden representar como una matriz unidimensional (es decir, un vector) y una matriz respectivamente. Esto permite representar la ecuación de Schrödinger en forma matricial. ${\displaystyle \psi _{E}}$ ${\displaystyle \psi _{E}}$ ${\displaystyle H}$

En este contexto, se suele utilizar la notación bra-ket . Un vector, que representa un estado del sistema, en el espacio de Hilbert de funciones integrables cuadradas se representa mediante . En esta notación, la ecuación de Schrödinger es: ${\displaystyle |\Psi _{E}\rangle }$

${\displaystyle H|\Psi _{E}\rangle =E|\Psi _{E}\rangle }$

donde es un estado propio de y representa el valor propio. es un operador autoadjunto observable , el análogo de dimensión infinita de las matrices hermíticas. Como en el caso de la matriz, en la ecuación anterior se entiende que es el vector obtenido por aplicación de la transformación a . ${\displaystyle |\Psi _{E}\rangle }$ ${\displaystyle H}$ ${\displaystyle E}$ ${\displaystyle H}$ ${\displaystyle H|\Psi _{E}\rangle }$ ${\displaystyle H}$ ${\displaystyle |\Psi _{E}\rangle }$

Transporte de ondas

La luz , las ondas acústicas y las microondas se dispersan aleatoriamente numerosas veces al atravesar un sistema estático desordenado. Aunque la dispersión múltiple aleatoriza repetidamente las ondas, en última instancia el transporte coherente de ondas a través del sistema es un proceso determinista que puede describirse mediante una matriz de transmisión de campo . ^{[44] [45]} Los vectores propios del operador de transmisión forman un conjunto de frentes de onda de entrada específicos del desorden que permiten que las ondas se acoplen en los canales propios del sistema desordenado: las vías independientes por las que las ondas pueden viajar a través del sistema. Los valores propios, , de corresponden a la transmitancia de intensidad asociada con cada canal propio. Una de las propiedades notables del operador de transmisión de los sistemas difusivos es su distribución de valores propios bimodal con y . ^[45] Además, una de las propiedades sorprendentes de los canales propios abiertos, más allá de la transmitancia perfecta, es el perfil espacial estadísticamente robusto de los canales propios. ^[46] ${\displaystyle \mathbf {t} }$ ${\displaystyle \mathbf {t} ^{\dagger }\mathbf {t} }$ ${\displaystyle \tau }$ ${\displaystyle \mathbf {t} ^{\dagger }\mathbf {t} }$ ${\displaystyle \tau _{\max }=1}$ ${\displaystyle \tau _{\min }=0}$

Orbitales moleculares

En mecánica cuántica , y en particular en física atómica y molecular , dentro de la teoría de Hartree-Fock , los orbitales atómicos y moleculares pueden definirse por los vectores propios del operador de Fock . Los valores propios correspondientes se interpretan como potenciales de ionización a través del teorema de Koopmans . En este caso, el término vector propio se utiliza en un sentido algo más general, ya que el operador de Fock depende explícitamente de los orbitales y sus valores propios. Por lo tanto, si se quiere subrayar este aspecto, se habla de problemas de valores propios no lineales. Tales ecuaciones se resuelven habitualmente mediante un procedimiento de iteración , llamado en este caso método de campo autoconsistente . En química cuántica , a menudo se representa la ecuación de Hartree-Fock en un conjunto de bases no ortogonales . Esta representación particular es un problema de valores propios generalizado llamado ecuaciones de Roothaan .

Geología y glaciología

En geología , especialmente en el estudio de till glacial , los vectores y valores propios se utilizan como un método por el cual una masa de información de la orientación y la inclinación de los constituyentes de un tejido de clastos se puede resumir en un espacio tridimensional mediante seis números. En el campo, un geólogo puede recopilar dichos datos para cientos o miles de clastos en una muestra de suelo, que solo se pueden comparar gráficamente, como en un diagrama Tri-Plot (Sneed y Folk), ^{[47] [48]} o como una red estereoscópica en una red Wulff. ^[49]

La salida para el tensor de orientación está en los tres ejes ortogonales (perpendiculares) del espacio. Los tres vectores propios están ordenados por sus valores propios ; ^[50] entonces es la orientación/inclinación primaria del clasto, es la secundaria y es la terciaria, en términos de resistencia. La orientación del clasto se define como la dirección del vector propio, en una rosa de los vientos de 360° . La inclinación se mide como el valor propio, el módulo del tensor: este se valora desde 0° (sin inclinación) hasta 90° (vertical). Los valores relativos de , , y están dictados por la naturaleza de la estructura del sedimento. Si , se dice que la estructura es isotrópica. Si , se dice que la estructura es plana. Si , se dice que la estructura es lineal. ^[51] ${\displaystyle \mathbf {v} _{1},\mathbf {v} _{2},\mathbf {v} _{3}}$ ${\displaystyle E_{1}\geq E_{2}\geq E_{3}}$ ${\displaystyle \mathbf {v} _{1}}$ ${\displaystyle \mathbf {v} _{2}}$ ${\displaystyle \mathbf {v} _{3}}$ ${\displaystyle E_{1}}$ ${\displaystyle E_{2}}$ ${\displaystyle E_{3}}$ ${\displaystyle E_{1}=E_{2}=E_{3}}$ ${\displaystyle E_{1}=E_{2}>E_{3}}$ ${\displaystyle E_{1}>E_{2}>E_{3}}$

Número básico de reproducción

El número básico de reproducción ( ) es un número fundamental en el estudio de cómo se propagan las enfermedades infecciosas. Si se incluye a una persona infecciosa en una población de personas completamente susceptibles, entonces es el número promedio de personas que una persona infecciosa típica infectará. El tiempo de generación de una infección es el tiempo, , desde que una persona se infecta hasta que la siguiente persona se infecta. En una población heterogénea, la matriz de próxima generación define cuántas personas de la población se infectarán después de que haya transcurrido el tiempo. El valor es entonces el valor propio más grande de la matriz de próxima generación. ^{[52] [53]} ${\displaystyle R_{0}}$ ${\displaystyle R_{0}}$ ${\displaystyle t_{G}}$ ${\displaystyle t_{G}}$ ${\displaystyle R_{0}}$

Caras propias

Caras propias como ejemplos de vectores propios

En el procesamiento de imágenes , las imágenes procesadas de rostros pueden verse como vectores cuyos componentes son los brillos de cada píxel . ^[54] La dimensión de este espacio vectorial es el número de píxeles. Los vectores propios de la matriz de covarianza asociada con un gran conjunto de imágenes normalizadas de rostros se denominan rostros propios ; este es un ejemplo de análisis de componentes principales . Son muy útiles para expresar cualquier imagen de rostro como una combinación lineal de algunos de ellos. En la rama de reconocimiento facial de la biometría , los rostros propios proporcionan un medio para aplicar compresión de datos a los rostros con fines de identificación . También se han realizado investigaciones relacionadas con sistemas de visión propia que determinan los gestos de las manos.

De manera similar a este concepto, las voces propias representan la dirección general de variabilidad en las pronunciaciones humanas de un enunciado particular, como una palabra en un idioma. Con base en una combinación lineal de dichas voces propias, se puede construir una nueva pronunciación de la palabra. Estos conceptos han resultado útiles en los sistemas de reconocimiento automático del habla para la adaptación del hablante.

Véase también

• Teoría de los antivalores propios
• Operador propio
• Plano propio
• Momentos propios
• Algoritmo de valores propios
• Estados cuánticos
• Forma normal de Jordania
• Lista de software de análisis numérico
• Problema propio no lineal
• Valor propio normal
• Problema de valor propio cuadrático
• Valor singular
• Espectro de una matriz

Notas

1. Nota:
   • En 1751, Leonhard Euler demostró que cualquier cuerpo tiene un eje principal de rotación: Leonhard Euler (presentado: octubre de 1751; publicado: 1760) "Du mouvement d'un corps solide quelconque lorsqu'il tourne autour d'un ax mobile" (Sobre el movimiento de cualquier cuerpo sólido mientras gira alrededor de un eje en movimiento), Histoire de l'Académie royale des sciences et des belles lettres de Berlin , págs. En la pág. 212, Euler demuestra que todo cuerpo contiene un eje principal de rotación: "Théorem. 44. De quelque figure que soit le corps, on y peut toujours asignator un tel axe, qui passe par son centre de gravité, autour duquel le corps peut tourner librement & d'un mouvement uniforme." (Teorema 44. Cualquiera que sea la forma del cuerpo, siempre se le puede asignar un eje que pase por su centro de gravedad, alrededor del cual pueda girar libremente y con un movimiento uniforme.)
   • En 1755, Johann Andreas Segner demostró que cualquier cuerpo tiene tres ejes principales de rotación: Johann Andreas Segner, Specimen theoriae turbinum [Ensayo sobre la teoría de las cimas (es decir, cuerpos giratorios)] ( Halle ("Halae"), (Alemania): Gebauer, 1755). (https://books.google.com/books?id=29 p. xxviii [29]), Segner deriva una ecuación de tercer grado en t , que demuestra que un cuerpo tiene tres ejes principales de rotación. Luego afirma (en la misma página): "Non autem repugnat tres esse eiusmodi positiones plani HM, quia in aequatione cubica radices tres esse possunt, et tres tangentis t valores". (Sin embargo, no es inconsistente que haya tres posiciones del plano HM, porque en ecuaciones cúbicas puede haber tres raíces y tres valores de la tangente t.)
   • El pasaje relevante de la obra de Segner fue analizado brevemente por Arthur Cayley . Véase: A. Cayley (1862) "Informe sobre el progreso de la solución de ciertos problemas especiales de dinámica", Informe de la trigésima segunda reunión de la Asociación Británica para el Avance de la Ciencia; celebrada en Cambridge en octubre de 1862 , 32 : 184-252; véanse especialmente las páginas 225-226.
2. Kline 1972, págs. 807–808 Augustin Cauchy (1839) "Mémoire sur l'intégration des équations linéaires" (Memoria sobre la integración de ecuaciones lineales), Comptes rendus , 8 : 827–830, 845–865, 889–907 , 931–937. De la pág. 827: "On sait d'ailleurs qu'en suivant la méthode de Lagrange, on obtient pour valeur générale de la variable prinicipale una fonction dans laquelle entrent avec la variable principale les racines d'une suree équation que j'appellerai l' équation caracteristique , el grado de esta ecuación es tan preciso como el orden de la ecuación diferente que es un agit d'intégrer." (Se sabe, además, que siguiendo el método de Lagrange se obtiene para el valor general de la variable principal una función en la que aparecen, junto con la variable principal, las raíces de una determinada ecuación que llamaré "ecuación característica". , siendo el grado de esta ecuación precisamente el orden de la ecuación diferencial que debe integrarse.)
3. Ver:
   • David Hilbert (1904) "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. (Erste Mitteilung)" (Fundamentos de una teoría general de ecuaciones integrales lineales. (Primer informe)), Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse ( Noticias de la Sociedad Filosófica de Göttingen, sección físico-matemática), págs. De la pág. 51: " Insbesondere in dieser ersten Mitteilung gelange ich zu Formeln, die die Entwickelung einer willkürlichen Funktion nach gewissen ausgezeichneten Funktionen, die ich 'Eigenfunktionen' nenne, liefern: ..." (En particular, en este primer informe llego a fórmulas que proporcionan el desarrollo [en serie] de una función arbitraria en términos de algunas funciones distintivas, que yo llamo funciones propias : ...) Más adelante en la misma página: "Dieser Erfolg ist wesentlich durch den Umstand bedingt, daß ich nicht, wie es bisher geschah , in erster Linie auf den Beweis für die Existenz der Eigenwerte ausgehe, ... " (Este éxito se debe principalmente al hecho de que, como ha ocurrido hasta ahora, no pretendo en primer lugar una prueba de la existencia de valores propios, ... )
   • Para el origen y evolución de los términos valor propio, valor característico, etc., véase: Usos más antiguos conocidos de algunas palabras de las matemáticas (E)
4. Para una prueba de este lema, véase Roman 2008, Teorema 8.2 en la pág. 186; Shilov 1977, pág. 109; Hefferon 2001, pág. 364; Beezer 2006, Teorema EDELI en la pág. 469; y Lema para la independencia lineal de vectores propios.
5. Al realizar la eliminación gaussiana sobre series de potencias formales truncadas en términos, es posible realizar operaciones, pero eso no tiene en cuenta la explosión combinatoria . ${\displaystyle n}$ ${\displaystyle O(n^{4})}$

Citas

1. Carga y ferias 1993, pág. 401.
2. Gilbert Strang. "6: Valores propios y vectores propios". Introducción al álgebra lineal (PDF) (5.ª ed.). Wellesley-Cambridge Press.
3. Herstein 1964, págs.228, 229.
4. Nering 1970, pág. 38.
5. Betteridge 1965.
6. "Vector propio y valor propio". www.mathsisfun.com . Consultado el 19 de agosto de 2020 .
7. Press et al. 2007, pág. 536.
8. Wolfram.com: Vector propio.
9. Nering 1970, pág. 107.
10. Hawkins 1975, §2.
11. Hawkins 1975, §3.
12. Kline 1972, pág. 673.
13. Kline 1972, págs. 807–808.
14. Kline 1972, págs. 715–716.
15. Kline 1972, págs. 706–707.
16. Kline 1972, pág. 1063, pág.
17. Aldrich 2006.
18. Francisco 1961, págs. 265-271.
19. Kublanovskaya 1962.
20. Préstamo Golub y Van 1996, §7.3.
21. Meyer 2000, §7.3.
22. Departamento de Matemáticas de la Universidad de Cornell (2016) Cursos de nivel inferior para estudiantes de primer y segundo año. Consultado el 27 de marzo de 2016.
23. Catálogo de cursos de matemáticas de la Universidad de Michigan (2016) Archivado el 1 de noviembre de 2015 en Wayback Machine . Consultado el 27 de marzo de 2016.
24. Press et al. 2007, pág. 38.
25. Fraleigh 1976, pág. 358.
26. Golub y Van Loan 1996, pág. 316.
27. Anton 1987, págs. 305, 307.
28. Beauregard y Fraleigh 1973, pág. 307.
29. Herstein 1964, pág. 272.
30. Nering 1970, págs. 115-116.
31. Herstein 1964, pág. 290.
32. Nering 1970, pág. 116.
33. Wolchover 2019.
34. Denton y col. 2022.
35. Van Mieghem 2014.
36. Van Mieghem 2024.
37. Korn y Korn 2000, sección 14.3.5a.
38. Friedberg, Insel y Spence 1989, pág. 217.
39. Romano 2008, pág. 186 §8
40. Nering 1970, pág. 107; Shilov 1977, pág. 109 Lema para el espacio propio
41. Lipschutz y Lipson 2002, pag. 111.
42. Romano 2008, pág. 189 §8.
43. Trefethen y Bau 1997.
44. Vellekoop y Mosk 2007, págs. 2309-2311.
45. Rotter y Gigan 2017, pág. 15005.
46. Bender y col. 2020, pág. 165901.
47. Graham y Midgley 2000, págs. 1473–1477.
48. Sneed & Folk 1958, págs. 114-150.
49. Knox-Robinson y Gardoll 1998, pág. 243.
50. Busche, cristiano; Schiller, Beate. "Geología endógena - Ruhr-Universität Bochum". www.ruhr-uni-bochum.de .
51. Benn y Evans 2004, págs. 103-107.
52. Diekmann, Heesterbeek y Metz 1990, págs. 365–382.
53. Heesterbeek y Diekmann 2000.
54. Xirouhakis, Votsis y Delopoulus 2004.

Fuentes

• Aldrich, John (2006), "Valor propio, función propia, vector propio y términos relacionados", en Miller, Jeff (ed.), Usos más antiguos conocidos de algunas de las palabras de las matemáticas
• Anton, Howard (1987), Álgebra lineal elemental (5.ª ed.), Nueva York: Wiley , ISBN 0-471-84819-0
• Beauregard, Raymond A.; Fraleigh, John B. (1973), Un primer curso de álgebra lineal: con introducción opcional a grupos, anillos y campos , Boston: Houghton Mifflin Co. , ISBN 0-395-14017-X
• Beezer, Robert A. (2006), Un primer curso de álgebra lineal, Libro gratuito en línea bajo licencia GNU, Universidad de Puget Sound
• Bender, Nicholas; Yamilov, Alexey; Yilmaz, Hasan; Cao, Hui (14 de octubre de 2020). "Fluctuaciones y correlaciones de los canales propios de transmisión en medios difusivos". Physical Review Letters . 125 (16): 165901. arXiv : 2004.12167 . Bibcode :2020PhRvL.125p5901B. doi :10.1103/physrevlett.125.165901. ISSN  0031-9007. PMID  33124845. S2CID  216553547.
• Benn, D.; Evans, D. (2004), Una guía práctica para el estudio de los sedimentos glaciales , Londres: Arnold, págs. 103-107
• Betteridge, Harold T. (1965), El nuevo diccionario alemán de Cassell , Nueva York: Funk & Wagnall , LCCN  58-7924
• Burden, Richard L.; Faires, J. Douglas (1993), Análisis numérico (5.ª ed.), Boston: Prindle, Weber y Schmidt, ISBN 0-534-93219-3
• Denton, Peter B.; Parke, Stephen J.; Tao, Terence; Zhang, Xining (enero de 2022). "Vectores propios a partir de valores propios: un estudio de una identidad básica en álgebra lineal" (PDF) . Boletín de la Sociedad Matemática Americana . 59 (1): 31–58. arXiv : 1908.03795 . doi :10.1090/bull/1722. S2CID  213918682. Archivado (PDF) desde el original el 19 de enero de 2022.
• Diekmann, O; Heesterbeek, JA; Metz, JA (1990), "Sobre la definición y el cálculo de la tasa básica de reproducción R0 en modelos de enfermedades infecciosas en poblaciones heterogéneas", Journal of Mathematical Biology , 28 (4): 365–382, doi :10.1007/BF00178324, hdl : 1874/8051 , PMID  2117040, S2CID  22275430
• Fraleigh, John B. (1976), Un primer curso de álgebra abstracta (2.ª ed.), Lectura: Addison-Wesley , ISBN 0-201-01984-1
• Francis, JGF (1961), "La transformación QR, I (parte 1)", The Computer Journal , 4 (3): 265–271, doi : 10.1093/comjnl/4.3.265
• Francis, JGF (1962), "La transformación QR, II (parte 2)", The Computer Journal , 4 (4): 332–345, doi : 10.1093/comjnl/4.4.332
• Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E. (1989), Álgebra lineal (2.ª ed.), Englewood Cliffs, NJ: Prentice Hall, ISBN 0-13-537102-3
• Golub, Gene H. ; Van Loan, Charles F. (1996), Cálculos matriciales (3.ª ed.), Baltimore, MD: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
• Graham, D.; Midgley, N. (2000), "Representación gráfica de la forma de las partículas mediante diagramas triangulares: un método de hoja de cálculo de Excel", Earth Surface Processes and Landforms , 25 (13): 1473–1477, Bibcode :2000ESPL...25.1473G, doi :10.1002/1096-9837(200012)25:13<1473::AID-ESP158>3.0.CO;2-C, S2CID  128825838
• Hawkins, T. (1975), "Cauchy y la teoría espectral de matrices", Historia Mathematica , 2 : 1–29, doi : 10.1016/0315-0860(75)90032-4
• Heesterbeek, JAP; Diekmann, Odo (2000), Epidemiología matemática de enfermedades infecciosas, serie Wiley en biología matemática y computacional, West Sussex, Inglaterra: John Wiley & Sons^{[ enlace muerto permanente ]}
• Hefferon, Jim (2001), Álgebra lineal, Colchester, VT: Libro en línea, St Michael's College
• Herstein, IN (1964), Temas de álgebra , Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
• Kline, Morris (1972), El pensamiento matemático desde la antigüedad hasta los tiempos modernos , Oxford University Press, ISBN 0-19-501496-0
• Knox-Robinson, C.; Gardoll, Stephen J. (1998), "GIS-stereoplot: un módulo interactivo de trazado de stereonet para el sistema de información geográfica ArcView 3.0", Computers & Geosciences , 24 (3): 243, Bibcode :1998CG.....24..243K, doi :10.1016/S0098-3004(97)00122-2
• Korn, Granino A.; Korn, Theresa M. (2000), "Manual matemático para científicos e ingenieros: definiciones, teoremas y fórmulas para referencia y revisión", Nueva York: McGraw-Hill (2.ª edición revisada), Bibcode :1968mhse.book.....K, ISBN 0-486-41147-8
• Kublanovskaya, Vera N. (1962), "Sobre algunos algoritmos para la solución del problema completo de valores propios", Matemáticas computacionales y física matemática de la URSS , 1 (3): 637–657, doi :10.1016/0041-5553(63)90168-X
• Lipschutz, Seymour; Lipson, Marc (12 de agosto de 2002). Esquema sencillo de álgebra lineal de Schaum. McGraw Hill Professional. pág. 111. ISBN 978-007139880-0.
• Meyer, Carl D. (2000), Análisis matricial y álgebra lineal aplicada , Filadelfia: Sociedad de Matemáticas Industriales y Aplicadas (SIAM), ISBN 978-0-89871-454-8
• Nering, Evar D. (1970), Álgebra lineal y teoría de matrices (2.ª ed.), Nueva York: Wiley , LCCN  76091646
• Prensa, William H.; Teukolsky, Saul A .; Vetterling, William T.; Flannery, Brian P. (2007), Recetas numéricas: el arte de la computación científica (3.ª ed.), Cambridge University Press, ISBN 978-0521880688
• Roman, Steven (2008), Álgebra lineal avanzada (3.ª ed.), Nueva York: Springer Science + Business Media, ISBN 978-0-387-72828-5
• Rotter, Stefan; Gigan, Sylvain (2 de marzo de 2017). "Campos de luz en medios complejos: la dispersión mesoscópica se encuentra con el control de ondas". Reseñas de Física Moderna . 89 (1): 015005. arXiv : 1702.05395 . Bibcode :2017RvMP...89a5005R. doi :10.1103/RevModPhys.89.015005. S2CID  119330480.
• Shilov, Georgi E. (1977), Álgebra lineal , Traducido y editado por Richard A. Silverman, Nueva York: Dover Publications, ISBN 0-486-63518-X
• Sneed, ED; Folk, RL (1958), "Guijarros en el bajo río Colorado, Texas, un estudio de morfogénesis de partículas", Journal of Geology , 66 (2): 114–150, Bibcode :1958JG.....66..114S, doi :10.1086/626490, S2CID  129658242
• Trefethen, Lloyd N.; Bau, David (1997), Álgebra lineal numérica , SIAM
• Van Mieghem, Piet (18 de enero de 2014). "Vectores propios de grafos, pesos fundamentales y métricas de centralidad para nodos en redes". arXiv : 1401.4580 [math.SP].
• Vellekoop, IM; Mosk, AP (15 de agosto de 2007). "Enfoque de luz coherente a través de medios opacos con fuerte dispersión". Optics Letters . 32 (16): 2309–2311. Bibcode :2007OptL...32.2309V. doi :10.1364/OL.32.002309. ISSN  1539-4794. PMID  17700768. S2CID  45359403.
• Weisstein, Eric W. "Eigenvector". mathworld.wolfram.com . Consultado el 4 de agosto de 2019 .
• Weisstein, Eric W. (nd). "Eigenvalue". mathworld.wolfram.com . Consultado el 19 de agosto de 2020 .
• Wolchover, Natalie (13 de noviembre de 2019). «Los neutrinos conducen a un descubrimiento inesperado en matemáticas básicas». Quanta Magazine . Consultado el 27 de noviembre de 2019 .
• Xirouhakis, A.; Votsis, G.; Delopoulus, A. (2004), Estimación del movimiento 3D y la estructura de rostros humanos (PDF) , Universidad Técnica Nacional de Atenas
• Van Mieghem, P. (2024). "Componentes de vectores propios de matrices simétricas relacionadas con grafos". Álgebra lineal y sus aplicaciones . 692 : 91–134. doi : 10.1016/j.laa.2024.03.035 .

Lectura adicional

• Golub, Gene F.; van der Vorst, Henk A. (2000), "Cálculo de valores propios en el siglo XX" (PDF) , Journal of Computational and Applied Mathematics , 123 (1–2): 35–65, Bibcode :2000JCoAM.123...35G, doi : 10.1016/S0377-0427(00)00413-1 , hdl :1874/2663
• Hill, Roger (2009). "λ – Valores propios". Sixty Symbols . Brady Haran para la Universidad de Nottingham .
• Kuttler, Kenneth (2017), Introducción al álgebra lineal (PDF) , Universidad Brigham Young
• Strang, Gilbert (1993), Introducción al álgebra lineal , Wellesley, MA: Wellesley-Cambridge Press, ISBN 0-9614088-5-5
• Strang, Gilbert (2006), Álgebra lineal y sus aplicaciones , Belmont, CA: Thomson, Brooks/Cole, ISBN 0-03-010567-6

Enlaces externos

• ¿Qué son los valores propios? – Introducción no técnica de la sección "Pregunte a los expertos" de PhysLink.com
• Ejemplos numéricos de valores propios y vectores propios: tutorial y programa interactivo de Revoledu.
• Introducción a los vectores propios y valores propios: conferencia de Khan Academy
• Vectores propios y valores propios | Esencia del álgebra lineal, capítulo 10 – Una explicación visual con 3Blue1Brown
• Calculadora de vectores propios de matrices de Symbolab (haga clic en el botón inferior derecho de la cuadrícula de 2×12 para seleccionar un tamaño de matriz. Seleccione un tamaño (para una matriz cuadrada), luego complete las entradas numéricamente y haga clic en el botón Ir. También puede aceptar números complejos). ${\displaystyle n\times n}$

La Wikiversidad utiliza la física introductoria para presentar los valores propios y los vectores propios.

Teoría

• Cálculo de valores propios
• Solución numérica de problemas de valores propios Editado por Zhaojun Bai, James Demmel , Jack Dongarra, Axel Ruhe y Henk van der Vorst