Paralelo (geometría)

Relación utilizada en geometría.

Dibujo lineal de líneas paralelas y curvas.

En geometría , las rectas paralelas son rectas infinitas coplanares que no se cruzan en ningún punto. Los planos paralelos son planos en el mismo espacio tridimensional que nunca se encuentran. Las curvas paralelas son curvas que no se tocan ni se cruzan y mantienen una distancia mínima fija. En el espacio euclidiano tridimensional, también se dice que una línea y un plano que no comparten un punto son paralelos. Sin embargo, dos líneas no coplanares se llaman líneas sesgadas . Los segmentos de recta y los vectores euclidianos son paralelos si tienen la misma dirección (no necesariamente la misma longitud).

Las líneas paralelas son el tema del postulado de las paralelas de Euclides . ^[1] El paralelismo es principalmente una propiedad de las geometrías afines y la geometría euclidiana es un ejemplo especial de este tipo de geometría. En algunas otras geometrías, como la geometría hiperbólica , las líneas pueden tener propiedades análogas a las que se hace referencia como paralelismo.

Símbolo

El símbolo paralelo es . ^{[2] [3]} Por ejemplo, indica que la línea AB es paralela a la línea  CD . ${\displaystyle \parallel }$ ${\displaystyle AB\parallel CD}$

En el juego de caracteres Unicode , los signos "paralelo" y "no paralelo" tienen puntos de código U+2225 (∥) y U+2226 (∦), respectivamente. Además, U+22D5 (⋕) representa la relación "igual y paralela a". ^[4]

El mismo símbolo se utiliza para una función binaria en ingeniería eléctrica (el operador paralelo ). Se diferencia de los corchetes de doble línea vertical , U+2016 (‖), que indican una norma (p. ej. ), así como del operador lógico u ( ) en varios lenguajes de programación. ${\displaystyle \|x\|}$||

paralelismo euclidiano

Dos líneas en un avión.

Condiciones para el paralelismo

Como lo muestran las marcas, las líneas a y b son paralelas. Esto se puede demostrar porque la transversal t produce ángulos correspondientes congruentes , que se muestran aquí a la derecha de la transversal, uno arriba y adyacente a la línea a y el otro arriba y adyacente a la línea b . ${\displaystyle \theta }$

Dadas las rectas paralelas l y m en el espacio euclidiano , las siguientes propiedades son equivalentes:

1. Cada punto de la línea m está ubicado exactamente a la misma distancia (mínima) de la línea l ( líneas equidistantes ).
2. La línea m está en el mismo plano que la línea l pero no corta a l (recuerde que las líneas se extienden hasta el infinito en cualquier dirección).
3. Cuando las líneas m y l son intersecadas por una tercera línea recta (una transversal ) en el mismo plano, los ángulos de intersección correspondientes con la transversal son congruentes .

Dado que estas son propiedades equivalentes, cualquiera de ellas podría tomarse como la definición de líneas paralelas en el espacio euclidiano, pero la primera y la tercera propiedades implican medición y, por lo tanto, son "más complicadas" que la segunda. Por tanto, la segunda propiedad es la que suele elegirse como propiedad definitoria de las rectas paralelas en la geometría euclidiana. ^[5] Las otras propiedades son entonces consecuencias del Postulado Paralelo de Euclides .

Historia

La definición de líneas paralelas como un par de líneas rectas en un plano que no se encuentran aparece como Definición 23 en el Libro I de los Elementos de Euclides . ^[6] Otros griegos discutieron definiciones alternativas, a menudo como parte de un intento de probar el postulado paralelo . Proclo atribuye a Posidonio una definición de líneas paralelas como líneas equidistantes y cita a Gémino en un tono similar. Simplicio también menciona la definición de Posidonio, así como su modificación por parte del filósofo Aganis. ^[6]

A finales del siglo XIX, en Inglaterra, los Elementos de Euclides todavía eran el libro de texto estándar en las escuelas secundarias. El tratamiento tradicional de la geometría estaba siendo presionado para cambiar por los nuevos desarrollos en geometría proyectiva y geometría no euclidiana , por lo que en ese momento se escribieron varios libros de texto nuevos para la enseñanza de la geometría. Una diferencia importante entre estos textos reformistas, tanto entre ellos como entre ellos y Euclides, es el tratamiento de las líneas paralelas. ^[7] Estos textos reformistas no estuvieron exentos de críticos y uno de ellos, Charles Dodgson (también conocido como Lewis Carroll ), escribió una obra de teatro, Euclides y sus rivales modernos , en la que arremete contra estos textos. ^[8]

Uno de los primeros libros de texto reformistas fue Geometría elemental de James Maurice Wilson de 1868. ^[9] Wilson basó su definición de líneas paralelas en la noción primitiva de dirección . Según Wilhelm Killing ^[10] la idea se remonta a Leibniz . ^[11] Wilson, sin definir dirección ya que es un primitivo, usa el término en otras definiciones como su sexta definición, "Dos líneas rectas que se encuentran tienen diferentes direcciones, y la diferencia de sus direcciones es el ángulo entre ellas. " Wilson (1868, p. 2) En la definición 15 introduce líneas paralelas de esta manera; "Las rectas que tienen la misma dirección , pero que no son partes de la misma recta, se llaman rectas paralelas ". Wilson (1868, p. 12) Augustus De Morgan revisó este texto y lo declaró un fracaso, principalmente sobre la base de esta definición y la forma en que Wilson la usó para probar cosas sobre líneas paralelas. Dodgson también dedica una gran parte de su obra (Acto II, Escena VI § 1) a denunciar el tratamiento que hace Wilson de los paralelos. Wilson eliminó este concepto de la tercera edición y posteriores de su texto. ^[12]

A otras propiedades, propuestas por otros reformadores, utilizadas como sustitutos de la definición de rectas paralelas, no les fue mucho mejor. La principal dificultad, como señaló Dodgson, era que para utilizarlos de esta manera era necesario añadir axiomas adicionales al sistema. La definición de línea equidistante de Posidonio, expuesta por Francis Cuthbertson en su texto de 1874 Geometría euclidiana, adolece del problema de que se debe demostrar que los puntos que se encuentran a una distancia fija dada en un lado de una línea recta forman una línea recta. Esto no se puede probar y se debe suponer que es cierto. ^[13] Los ángulos correspondientes formados por una propiedad transversal, utilizada por WD Cooley en su texto de 1860, Los elementos de la geometría, simplificada y explicada requiere una prueba del hecho de que si una transversal corta un par de líneas en ángulos correspondientes congruentes, entonces todas los transversales deben hacerlo. Nuevamente, se necesita un nuevo axioma para justificar esta afirmación.

Construcción

Las tres propiedades anteriores conducen a tres métodos diferentes de construcción ^[14] de líneas paralelas.

El problema: trazar una recta que pase por una paralela a l .

• 
  Propiedad 1: La línea m tiene en todas partes la misma distancia a la línea l .
• 
  Propiedad 2: Tome una línea aleatoria que pase por a y que corte a l en x . Mueve el punto x al infinito.
• 
  Propiedad 3: Tanto l como m comparten una línea transversal que pasa por a y los intersecta en 90°.

Distancia entre dos líneas paralelas

Debido a que las líneas paralelas en un plano euclidiano son equidistantes, existe una distancia única entre las dos líneas paralelas. Dadas las ecuaciones de dos rectas paralelas no verticales ni horizontales,

${\displaystyle y=mx+b_{1}\,}$

${\displaystyle y=mx+b_{2}\,,}$

La distancia entre las dos líneas se puede encontrar ubicando dos puntos (uno en cada línea) que se encuentran en una perpendicular común a las líneas paralelas y calculando la distancia entre ellas. Como las rectas tienen pendiente m , una perpendicular común tendría pendiente −1/ m y podemos tomar la recta con ecuación y = − x / m como perpendicular común. Resuelve los sistemas lineales.

${\displaystyle {\begin{cases}y=mx+b_{1}\\y=-x/m\end{cases}}}$

y

${\displaystyle {\begin{cases}y=mx+b_{2}\\y=-x/m\end{cases}}}$

para obtener las coordenadas de los puntos. Las soluciones de los sistemas lineales son los puntos.

${\displaystyle \left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2}+1}},{\frac {b_{1}}{m^{2}+1}}\right)\,}$

y

${\displaystyle \left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2}+1}},{\frac {b_{2}}{m^{2}+1}}\right).}$

Estas fórmulas aún dan las coordenadas correctas de los puntos incluso si las líneas paralelas son horizontales (es decir, m = 0). La distancia entre los puntos es

${\displaystyle d={\sqrt {\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}}={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,,}$

lo que se reduce a

${\displaystyle d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,.}$

Cuando las rectas están dadas por la forma general de la ecuación de una recta (se incluyen las rectas horizontales y verticales):

${\displaystyle ax+by+c_{1}=0\,}$

${\displaystyle ax+by+c_{2}=0,\,}$

su distancia se puede expresar como

${\displaystyle d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.}$

Dos líneas en un espacio tridimensional.

Dos líneas en el mismo espacio tridimensional que no se cruzan no tienen por qué ser paralelas. Sólo si están en un plano común se les llama paralelos; de lo contrario se llaman líneas sesgadas .

Dos líneas distintas l y m en el espacio tridimensional son paralelas si y solo si la distancia desde un punto P en la línea m al punto más cercano en la línea l es independiente de la ubicación de P en la línea m . Esto nunca es válido para líneas sesgadas.

Una recta y un plano.

Una recta m y un plano q en el espacio tridimensional, la recta que no se encuentra en ese plano, son paralelos si y sólo si no se cruzan.

De manera equivalente, son paralelos si y sólo si la distancia desde un punto P en la línea m al punto más cercano en el plano q es independiente de la ubicación de P en la línea m .

dos aviones

De manera similar a que las líneas paralelas deben estar ubicadas en el mismo plano, los planos paralelos deben estar situados en el mismo espacio tridimensional y no contener ningún punto en común.

Dos planos distintos q y r son paralelos si y sólo si la distancia desde un punto P en el plano q al punto más cercano en el plano r es independiente de la ubicación de P en el plano q . Esto nunca se cumplirá si los dos planos no están en el mismo espacio tridimensional.

En geometría no euclidiana

En geometría no euclidiana , el concepto de línea recta es reemplazado por el concepto más general de geodésica , una curva que es localmente recta con respecto a la métrica (definición de distancia) en una variedad de Riemann , una superficie (o superior). espacio dimensional) que a su vez puede ser curvo. En la relatividad general , las partículas que no están bajo la influencia de fuerzas externas siguen las geodésicas en el espacio-tiempo , una variedad de cuatro dimensiones con 3 dimensiones espaciales y 1 dimensión temporal. ^[15]

En geometría no euclidiana ( geometría elíptica o hiperbólica ), las tres propiedades euclidianas mencionadas anteriormente no son equivalentes y solo la segunda (la línea m está en el mismo plano que la línea l pero no cruza a l) es útil en geometrías no euclidianas. ya que no implica mediciones. En geometría general, las tres propiedades anteriores dan tres tipos diferentes de curvas, curvas equidistantes , geodésicas paralelas y geodésicas que comparten una perpendicular común , respectivamente.

Geometría hiperbólica

Intersección de rectas paralelas y ultraparalelas que pasan por a con respecto a l en el plano hiperbólico. Las líneas paralelas parecen cruzarse con l justo al lado de la imagen. Esto es sólo un artefacto de la visualización. En un plano hiperbólico real, las líneas se acercarán entre sí y se "encontrarán" en el infinito.

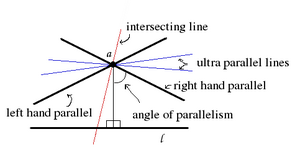
Mientras que en la geometría euclidiana dos geodésicas pueden cruzarse o ser paralelas, en la geometría hiperbólica hay tres posibilidades. Dos geodésicas pertenecientes al mismo plano pueden ser:

1. intersectándose , si se cruzan en un punto común del plano,
2. paralelo , si no se cruzan en el plano, pero convergen a un punto límite común en el infinito ( punto ideal ), o
3. ultraparalelos , si no tienen un punto límite común en el infinito.

En la literatura, las geodésicas ultraparalelas a menudo se denominan no intersecantes . Las geodésicas que se cruzan en el infinito se llaman paralelas limitantes .

Como en la ilustración, a través de un punto a que no está en la línea l, hay dos líneas paralelas limitantes , una para cada dirección del punto ideal de la línea l. Separan las líneas que cruzan la línea l y las que son ultra paralelas a la línea l .

Las líneas ultraparalelas tienen una única perpendicular común ( teorema ultraparalelo ) y divergen en ambos lados de esta perpendicular común.

Geometría esférica o elíptica

En la esfera no existe ninguna línea paralela. La línea a es un círculo máximo , el equivalente a una línea recta en geometría esférica. La línea c es equidistante de la línea a pero no es un círculo máximo. Es un paralelo de latitud. La línea b es otra geodésica que corta a a en dos puntos antípodas. Comparten dos perpendiculares comunes (una se muestra en azul).

En geometría esférica , todas las geodésicas son círculos máximos . Los círculos máximos dividen la esfera en dos hemisferios iguales y todos los círculos máximos se cruzan entre sí. Por lo tanto, no existen geodésicas paralelas a una geodésica determinada, ya que todas las geodésicas se cruzan. Las curvas equidistantes en la esfera se llaman paralelos de latitud , análogas a las líneas de latitud en un globo terráqueo. Los paralelos de latitud se pueden generar mediante la intersección de la esfera con un plano paralelo a un plano que pasa por el centro de la esfera.

Variante reflexiva

Si l, m, n son tres líneas distintas, entonces ${\displaystyle l\parallel m\ \land \ m\parallel n\ \implies \ l\parallel n.}$

En este caso, el paralelismo es una relación transitiva . Sin embargo, en el caso l = n , las líneas superpuestas no se consideran paralelas en la geometría euclidiana. La relación binaria entre rectas paralelas es evidentemente una relación simétrica . Según los principios de Euclides, el paralelismo no es una relación reflexiva y, por tanto, no puede ser una relación de equivalencia . Sin embargo, en geometría afín un lápiz de rectas paralelas se toma como clase de equivalencia en el conjunto de rectas donde el paralelismo es una relación de equivalencia. ^{[16] [17] [18]}

Para ello, Emil Artin (1957) adoptó una definición de paralelismo según la cual dos rectas son paralelas si tienen todos o ninguno de sus puntos en común. ^[19] Entonces una recta es paralela a sí misma de modo que las propiedades reflexiva y transitiva pertenecen a este tipo de paralelismo, creando una relación de equivalencia en el conjunto de rectas. En el estudio de la geometría de incidencia , se utiliza esta variante de paralelismo en el plano afín .

Ver también

• Paralelo de Clifford
• Colinealidad
• Líneas concurrentes
• Limitar el paralelo
• Curva paralela
• Teorema ultraparalelo

Notas

1. Aunque este postulado solo se refiere al momento en que las rectas se encuentran, es necesario para demostrar la unicidad de las rectas paralelas en el sentido del axioma de Playfair .
2. Kersey (la mayor), John (1673). Álgebra . vol. Libro IV. Londres. pag. 177.
3. Cajori, Florian (1993) [septiembre de 1928]. "§ 184, § 359, § 368". Una historia de las notaciones matemáticas: notaciones en matemáticas elementales. vol. 1 (dos volúmenes en una reimpresión inalterada). Chicago, EE. UU.: editorial Open Court . págs.193, 402–403, 411–412. ISBN 0-486-67766-4. LCCN  93-29211 . Consultado el 22 de julio de 2019 . §359. […] ∥ porque el paralelo aparece en Opuscula mathematica hactenus inedita (1677) de Oughtred [p. 197], obra póstuma (§ 184) […] §368. Señales de líneas paralelas. […] cuando el signo de igualdad de Recorde se abrió paso en el continente, se empezaron a utilizar líneas verticales para el paralelismo. Encontramos ∥ para "paralelo" en Kersey ,[14] Caswell , Jones ,[15] Wilson,[16] Emerson ,[17] Kambly,[18] y los escritores de los últimos cincuenta años que ya han sido citados en relación con con otras pictografías. Antes de 1875 aproximadamente no ocurre con tanta frecuencia […] Hall y Stevens[1] usan "par[1] o ∥" para paralelo […] [14] John Kersey , Algebra (Londres, 1673), Libro IV, p. 177. [15] W. Jones , Synopsis palmarioum matheseos (Londres, 1706). [16] John Wilson, Trigonometría (Edimburgo, 1714), explicación de los personajes. [17] W. Emerson , Elementos de geometría (Londres, 1763), p. 4. [18] L. Kambly  [de] , Die Elementar-Mathematik , Parte 2: Planimetrie , 43. edición (Breslau, 1876), p. 8. […] [1] HS Hall y FH Stevens, Euclid's Elements , Partes I y II (Londres, 1889), p. 10. […][1]
4. "Operadores matemáticos - Consorcio Unicode" (PDF) . Consultado el 21 de abril de 2013 .
5. Wylie 1964, págs.92—94
6. Heath 1956, págs. 190-194
7. Richards 1988, cap. 4: Euclides y el escolar inglés. págs. 161-200
8. Carroll, Lewis (2009) [1879], Euclides y sus rivales modernos , Barnes & Noble, ISBN 978-1-4351-2348-9
9. Wilson 1868
10. Einführung in die Grundlagen der Geometrie, I , p. 5
11. Salud 1956, pag. 194
12. Richards 1988, págs. 180-184
13. Salud 1956, pag. 194
14. Sólo el tercero es una construcción con regla y compás, los dos primeros son procesos infinitos (requieren un "número infinito de pasos").
15. Iglesia, Benjamín (3 de diciembre de 2022). "Una introducción no tan amable a la relatividad general" (PDF) .
16. HSM Coxeter (1961) Introducción a la geometría , p. 192, John Wiley & Sons
17. Wanda Szmielew (1983) De la geometría afín a la euclidiana , p. 17, D. Reidel ISBN 90-277-1243-3 
18. Andy Liu (2011) "¿Es el paralelismo una relación de equivalencia?", The College Mathematics Journal 42(5):372
19. Emil Artin (1957) Álgebra geométrica, página 52 vía Internet Archive

Referencias

• Heath, Thomas L. (1956), Los trece libros de los elementos de Euclides (2ª ed. [facsímil. Publicación original: Cambridge University Press, 1925] ed.), Nueva York: Dover Publications

(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). Traducción autorizada de Heath además de una extensa investigación histórica y comentarios detallados a lo largo del texto.   

• Richards, Joan L. (1988), Visiones matemáticas: la búsqueda de la geometría en la Inglaterra victoriana , Boston: Academic Press, ISBN 0-12-587445-6
• Wilson, James Maurice (1868), Geometría elemental (1ª ed.), Londres: Macmillan and Co.
• Wylie, CR Jr. (1964), Fundamentos de la geometría , McGraw-Hill

Otras lecturas

• Papadopoulos, Atanase; Théret, Guillaume (2014), La théorie des parallèles de Johann Heinrich Lambert: presentación, traducción y comentarios , París: Colección Sciences dans l'histoire, Librairie Albert Blanchard, ISBN 978-2-85367-266-5

enlaces externos