Relación matemática
Otro ejemplo puede ayudar a clarificar el concepto: "ser hermana de" es una relación en el conjunto de todas las personas, que se cumple, por ejemplo, entre Marie Curie y Bronisława Dłuska, y viceversa.
A continuación se mencionan algunas propiedades de las relaciones: Por ejemplo, "es menor que" es una relación irreflexiva, asimétrica y transitiva, pero no reflexiva ni simétrica.
Se han declarado numerosos teoremas matemáticos sobre combinaciones de propiedades de relación, como "Una relación transitiva es irreflexiva si, y solo si, es asimétrica".
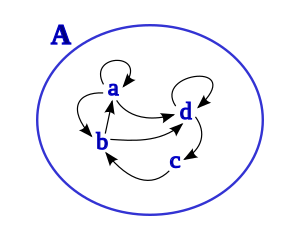
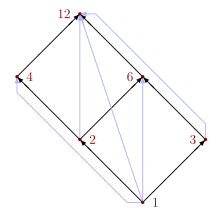
Una relación R sobre un conjunto finito X puede representarse como: Una relación transitiva[nota 3] R en un conjunto finito X también se puede representar como: Por ejemplo, en el conjunto de todos los divisores de 12, se define la relación Rdiv mediante Formalmente, X = { 1, 2, 3, 4, 6, 12 } y Rdiv = { (1,2), (1,3), (1,4), (1 ,6), (1,12), (2,4), (2,6), (2,12), (3,6), (3,12), (4,12), (6,12 ) }.
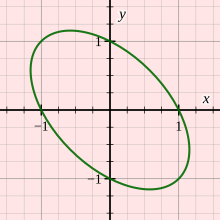
Las siguientes expresiones son equivalentes: Como otro ejemplo, se define la relación Rel en ℝ mediante: La representación de Rel como un gráfico 2D genera una elipse (véase la imagen de la derecha).
Algunas propiedades importantes que puede tener una relación R sobre un conjunto X son: Las 2 alternativas anteriores no son exhaustivas; por ejemplo, la relación roja y= x2 que se muestra en el siguiente diagrama no es irreflexiva ni reflexiva, ya que contiene el par (0, 0), pero no (2, 2), respectivamente.
Nuevamente, las tres alternativas anteriores están lejos de ser exhaustivas.
si R es un subconjunto de S, es decir, para todo
[1][9] Cuando X= Y, se obtiene el concepto de relación descrito anteriormente; a menudo se le llama relación homogénea (o endorelación)[18][19] para distinguirla de su generalización.
Un ejemplo de relación heterogénea es "el océano x limita con el continente y".
Los ejemplos más conocidos son las funciones[nota 6] con distintos dominios y rangos, como sucede con la relación