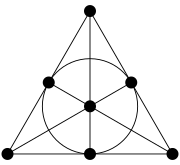
Estructura de incidencia

Incluso en un entorno geométrico, las estructuras de incidencia no se limitan solo a puntos y rectas; y se pueden utilizar objetos de dimensiones superiores (planos, sólidos, espacios n-dimensionales, o superficies cónicas).[1]​ Una estructura de incidencia es una tripleta (P, L, I) donde P es un conjunto cuyos elementos se llaman puntos, L es un conjunto distinto cuyos elementos se llaman líneas y I ⊆ P × L es la relación de incidencia.Cada uno de estos ejemplos, excepto el segundo, es uniforme (con tres puntos por línea).Las estructuras de incidencia rara vez se estudian en toda su generalidad, y es típico centrarse en aquellas que satisfacen algunos axiomas adicionales.Por ejemplo, un espacio lineal parcial es una estructura de incidencia que satisface: Si el primer axioma anterior se reemplaza por la condición más fuerte: la estructura de incidencia resultante se denomina espacio lineal.[2]​ Una estructura C que es un isomorfismo con respecto a su dual C∗, se denomina autodual.Si todos los subconjuntos en F tienen el mismo tamaño, el diseño del bloque se llama "uniforme".Si los conjuntos P y L son finitos, estas representaciones pueden codificar de forma compacta toda la información relevante relativa a la estructura.Compárese esto con la geometría ordenada, donde sí existe el concepto de posición intermedia.En particular, no es necesario representalas mediante "segmentos de recta" (véanse los ejemplos 1, 3 y 4 anteriores).Algunas estructuras de incidencia admiten representación mediante puntos y líneas rectas.Las estructuras que pueden serlo se denominan "factibles" o "realizables".El plano de Fano (ejemplo 1 anterior) no es factible, ya que necesita al menos una curva.Dado que el grafo de Heawood es conexo e isogonal, existe un automorfismo (como el definido por una reflexión sobre el eje vertical en la figura del grafo de Heawood) que intercambia vértices blancos y negros.Esto, a su vez, implica que el plano Fano es autodual.