Teorema de Pitágoras

Relación entre los lados de un triángulo rectángulo

En matemáticas , el teorema de Pitágoras o teorema de Pitágoras es una relación fundamental en la geometría euclidiana entre los tres lados de un triángulo rectángulo . Establece que el área del cuadrado cuyo lado es la hipotenusa (el lado opuesto al ángulo recto ) es igual a la suma de las áreas de los cuadrados de los otros dos lados.

El teorema se puede escribir como una ecuación que relaciona las longitudes de los lados a , b y la hipotenusa c , a veces llamada ecuación de Pitágoras : ^[1]

${\displaystyle a^{2}+b^{2}=c^{2}.}$

El teorema recibe su nombre del filósofo griego Pitágoras , nacido alrededor del año 570 a. C. El teorema se ha demostrado en numerosas ocasiones mediante distintos métodos, posiblemente la mayor cantidad de pruebas realizadas hasta la fecha para un teorema matemático. Las pruebas son diversas e incluyen tanto pruebas geométricas como algebraicas , y algunas datan de hace miles de años.

Cuando el espacio euclidiano se representa mediante un sistema de coordenadas cartesianas en geometría analítica , la distancia euclidiana satisface la relación pitagórica: la distancia al cuadrado entre dos puntos es igual a la suma de los cuadrados de la diferencia de cada coordenada entre los puntos.

El teorema se puede generalizar de varias maneras: a espacios de dimensiones superiores , a espacios que no son euclidianos , a objetos que no son triángulos rectángulos y a objetos que no son triángulos en absoluto sino sólidos n -dimensionales .

Demostraciones utilizando cuadrados construidos

Demostración del teorema de Pitágoras mediante reordenamiento.
(El área del espacio en blanco permanece constante durante todo el reordenamiento de traslación de los triángulos. En todo momento, el área es siempre c² . Y, de la misma manera, en todo momento, el área es siempre a²+b² .)

Pruebas de reordenamiento

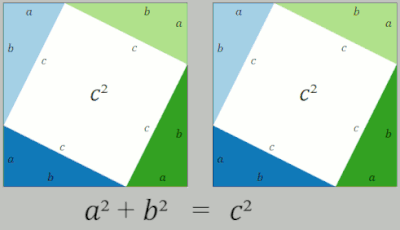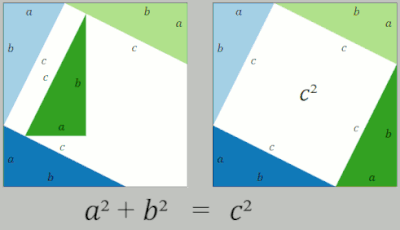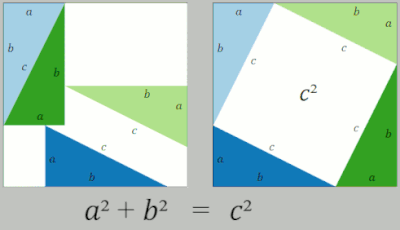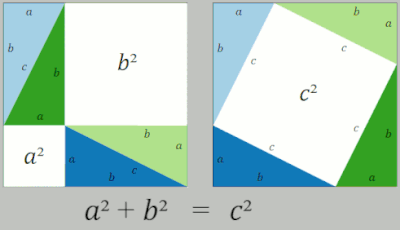
En una prueba de reordenamiento, se utilizan dos cuadrados cuyos lados tienen una medida de y que contienen cuatro triángulos rectángulos cuyos lados son a , b y c , siendo la hipotenusa c . En el cuadrado del lado derecho, los triángulos se colocan de manera que las esquinas del cuadrado correspondan a las esquinas del ángulo recto en los triángulos, formando un cuadrado en el centro cuyos lados tienen una longitud c . Cada cuadrado exterior tiene un área de así como , con representando el área total de los cuatro triángulos. Dentro del cuadrado grande del lado izquierdo, los cuatro triángulos se mueven para formar dos rectángulos similares con lados de longitud a y b . Estos rectángulos en su nueva posición ahora han delineado dos nuevos cuadrados, uno con una longitud de lado a se forma en la esquina inferior izquierda, y otro cuadrado con una longitud de lado b se forma en la esquina superior derecha. En esta nueva posición, este lado izquierdo ahora tiene un cuadrado de área así como . Dado que ambos cuadrados tienen el área de se deduce que la otra medida del área del cuadrado también son iguales entre sí de manera que = . Con el área de los cuatro triángulos eliminada de ambos lados de la ecuación, lo que queda es ^[2] ${\displaystyle a+b}$ ${\displaystyle (a+b)^{2}}$ ${\displaystyle 2ab+c^{2}}$ ${\displaystyle 2ab}$ ${\displaystyle (a+b)^{2}}$ ${\displaystyle 2ab+a^{2}+b^{2}}$ ${\displaystyle (a+b)^{2}}$ ${\displaystyle 2ab+c^{2}}$ ${\displaystyle 2ab+a^{2}+b^{2}}$ ${\displaystyle a^{2}+b^{2}=c^{2}.}$

En otra prueba, los rectángulos en la segunda caja también se pueden colocar de manera que ambos tengan una esquina que corresponda a esquinas consecutivas del cuadrado. De esta manera, también forman dos cajas, esta vez en esquinas consecutivas, con áreas y que nuevamente darán lugar a un segundo cuadrado de con el área . ${\displaystyle a^{2}}$ ${\displaystyle b^{2}}$ ${\displaystyle 2ab+a^{2}+b^{2}}$

El matemático inglés Sir Thomas Heath ofrece esta prueba en su comentario a la Proposición I.47 de los Elementos de Euclides , y menciona las propuestas de los matemáticos alemanes Carl Anton Bretschneider y Hermann Hankel de que Pitágoras pudo haber conocido esta prueba. El propio Heath está a favor de una propuesta diferente para una prueba pitagórica, pero reconoce desde el principio de su discusión "que la literatura griega que poseemos perteneciente a los primeros cinco siglos posteriores a Pitágoras no contiene ninguna declaración que especifique este o cualquier otro gran descubrimiento geométrico particular de él". ^[3] Los estudios recientes han puesto cada vez más en duda cualquier tipo de papel para Pitágoras como creador de las matemáticas, aunque el debate sobre esto continúa. ^[4]

Pruebas algebraicas

Diagrama de las dos pruebas algebraicas

El teorema se puede demostrar algebraicamente utilizando cuatro copias del mismo triángulo dispuestas simétricamente alrededor de un cuadrado de lado c , como se muestra en la parte inferior del diagrama. ^[5] Esto da como resultado un cuadrado más grande, con lado a + b y área ( a + b ) ² . Los cuatro triángulos y el lado cuadrado c deben tener la misma área que el cuadrado más grande,

${\displaystyle (b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,}$

donación

${\displaystyle c^{2}=(b+a)^{2}-2ab=b^{2}+2ab+a^{2}-2ab=a^{2}+b^{2}.}$

Una prueba similar utiliza cuatro copias de un triángulo rectángulo con lados a , b y c , dispuestos dentro de un cuadrado con lado c como en la mitad superior del diagrama. ^[6] Los triángulos son similares con área , mientras que el cuadrado pequeño tiene lado b − a y área ( b − a ) ² . Por lo tanto, el área del cuadrado grande es ${\displaystyle {\tfrac {1}{2}}ab}$

${\displaystyle (b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=b^{2}-2ab+a^{2}+2ab=a^{2}+b^{2}.}$

Pero este es un cuadrado con lado c y área c ² , entonces

${\displaystyle c^{2}=a^{2}+b^{2}.}$

Otras demostraciones del teorema

Este teorema puede tener más pruebas conocidas que cualquier otro (la ley de reciprocidad cuadrática es otro candidato para esa distinción); el libro La proposición pitagórica contiene 370 pruebas. ^[7]

Demostración utilizando triángulos semejantes

Demostración utilizando triángulos semejantes

Esta prueba se basa en la proporcionalidad de los lados de tres triángulos semejantes , es decir, en el hecho de que la relación entre dos lados correspondientes de triángulos semejantes es la misma independientemente del tamaño de los triángulos.

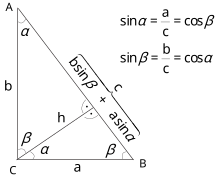
Sea ABC un triángulo rectángulo, cuyo ángulo recto se encuentra en C , como se muestra en la figura. Dibuje la altura desde el punto C y llame H a su intersección con el lado AB . El punto H divide la longitud de la hipotenusa c en las partes d y e . El nuevo triángulo, ACH, es similar al triángulo ABC , porque ambos tienen un ángulo recto (por definición de la altura) y comparten el ángulo en A , lo que significa que el tercer ángulo también será el mismo en ambos triángulos, marcado como θ en la figura. Por un razonamiento similar, el triángulo CBH también es similar a ABC . La prueba de semejanza de los triángulos requiere el postulado del triángulo : La suma de los ángulos en un triángulo es dos ángulos rectos, y es equivalente al postulado de las paralelas . La semejanza de los triángulos conduce a la igualdad de razones de los lados correspondientes:

${\displaystyle {\frac {BC}{AB}}={\frac {BH}{BC}}{\text{ and }}{\frac {AC}{AB}}={\frac {AH}{AC}}.}$

El primer resultado iguala los cosenos de los ángulos θ , mientras que el segundo resultado iguala sus senos .

Estas proporciones se pueden escribir como

${\displaystyle BC^{2}=AB\times BH{\text{ and }}AC^{2}=AB\times AH.}$

Sumando estas dos igualdades obtenemos como resultado

${\displaystyle BC^{2}+AC^{2}=AB\times BH+AB\times AH=AB(AH+BH)=AB^{2},}$

que, después de la simplificación, demuestra el teorema de Pitágoras:

${\displaystyle BC^{2}+AC^{2}=AB^{2}.}$

El papel de esta prueba en la historia es objeto de mucha especulación. La pregunta subyacente es por qué Euclides no utilizó esta prueba, sino que inventó otra. Una conjetura es que la prueba por triángulos semejantes implicaba una teoría de proporciones, un tema que no se trató hasta más tarde en los Elementos , y que la teoría de proporciones necesitaba un mayor desarrollo en ese momento. ^[8]

Demostración de Einstein por disección sin reordenamiento

Triángulo rectángulo sobre la hipotenusa diseccionado en dos triángulos rectángulos similares sobre los catetos, según la prueba de Einstein.

Albert Einstein dio una prueba por disección en la que no es necesario mover las piezas. ^[9] En lugar de utilizar un cuadrado sobre la hipotenusa y dos cuadrados sobre los catetos, se puede utilizar cualquier otra forma que incluya la hipotenusa, y dos formas similares que incluyan cada una uno de los dos catetos en lugar de la hipotenusa (véase Figuras similares en los tres lados). En la prueba de Einstein, la forma que incluye la hipotenusa es el propio triángulo rectángulo. La disección consiste en dejar caer una perpendicular desde el vértice del ángulo recto del triángulo hasta la hipotenusa, dividiendo así todo el triángulo en dos partes. Esas dos partes tienen la misma forma que el triángulo rectángulo original, y tienen los catetos del triángulo original como sus hipotenusas, y la suma de sus áreas es la del triángulo original. Debido a que la relación entre el área de un triángulo rectángulo y el cuadrado de su hipotenusa es la misma para triángulos similares, la relación entre las áreas de los tres triángulos se cumple también para los cuadrados de los lados del triángulo grande.

Prueba de Euclides

Demostración en los Elementos de Euclides

En resumen, así es como procede la prueba en los Elementos de Euclides . El cuadrado grande se divide en un rectángulo izquierdo y otro derecho. Se construye un triángulo que tiene la mitad del área del rectángulo izquierdo. Luego se construye otro triángulo que tiene la mitad del área del cuadrado en el lado más a la izquierda. Se demuestra que estos dos triángulos son congruentes , lo que demuestra que este cuadrado tiene la misma área que el rectángulo izquierdo. A este argumento le sigue una versión similar para el rectángulo derecho y el cuadrado restante. Al unir los dos rectángulos para reformar el cuadrado sobre la hipotenusa, su área es la misma que la suma del área de los otros dos cuadrados. A continuación se presentan los detalles.

Sean A , B , C los vértices de un triángulo rectángulo, con un ángulo recto en A. Traza una perpendicular desde A hasta el lado opuesto a la hipotenusa en el cuadrado sobre la hipotenusa. Esa línea divide el cuadrado sobre la hipotenusa en dos rectángulos, cada uno con la misma área que uno de los dos cuadrados sobre los catetos.

Para la prueba formal, necesitamos cuatro lemas elementales :

1. Si dos triángulos tienen dos lados de uno iguales a dos lados del otro, cada uno a cada uno, y los ángulos comprendidos por esos lados son iguales, entonces los triángulos son congruentes ( lado-ángulo-lado ).
2. El área de un triángulo es la mitad del área de cualquier paralelogramo de la misma base y con la misma altura.
3. El área de un rectángulo es igual al producto de dos lados adyacentes.
4. El área de un cuadrado es igual al producto de dos de sus lados (se deduce de 3).

A continuación, cada cuadrado superior está relacionado con un triángulo congruente con otro triángulo relacionado a su vez con uno de los dos rectángulos que forman el cuadrado inferior. ^[10]

Ilustración que incluye las nuevas líneas

Mostrando los dos triángulos congruentes de la mitad del área del rectángulo BDLK y el cuadrado BAGF

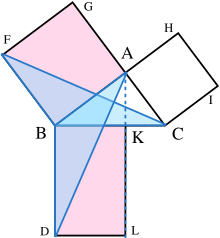
La prueba es la siguiente:

1. Sea ACB un triángulo rectángulo con ángulo recto CAB.
2. En cada uno de los lados BC, AB y CA se dibujan los cuadrados CBDE, BAGF y ACIH, en ese orden. La construcción de los cuadrados requiere los teoremas inmediatamente anteriores de Euclides y depende del postulado de las paralelas. ^[11]
3. Desde A, traza una línea paralela a BD y CE. Intersectará perpendicularmente a BC y DE en K y L, respectivamente.
4. Unir CF y AD, para formar los triángulos BCF y BDA.
5. Los ángulos CAB y BAG son ambos ángulos rectos; por lo tanto, C, A y G son colineales .
6. Los ángulos CBD y FBA son ambos ángulos rectos; por lo tanto, el ángulo ABD es igual al ángulo FBC, ya que ambos son la suma de un ángulo recto y un ángulo ABC.
7. Como AB es igual a FB, BD es igual a BC y el ángulo ABD es igual al ángulo FBC, el triángulo ABD debe ser congruente con el triángulo FBC.
8. Como AKL es una línea recta paralela a BD, entonces el rectángulo BDLK tiene el doble del área del triángulo ABD porque comparten la base BD y tienen la misma altura BK, es decir, una línea normal a su base común, que conecta las líneas paralelas BD y AL. (lema 2)
9. Como C es colineal con A y G, y esta línea es paralela a FB, entonces el cuadrado BAGF debe tener el doble de área que el triángulo FBC.
10. Por lo tanto, el rectángulo BDLK debe tener la misma área que el cuadrado BAGF = AB ² .
11. Aplicando los pasos 3 a 10 al otro lado de la figura, se puede demostrar de manera similar que el rectángulo CKLE debe tener la misma área que el cuadrado ACIH = AC ² .
12. Sumando estos dos resultados, AB ² + AC ² = BD × BK + KL × KC
13. Como BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
14. Por lo tanto, AB ² + AC ² = BC ² , ya que CBDE es un cuadrado.

Esta prueba, que aparece en los Elementos de Euclides como la de la Proposición 47 del Libro 1, demuestra que el área del cuadrado sobre la hipotenusa es la suma de las áreas de los otros dos cuadrados. ^{[12] [13]} Esto es bastante distinto de la prueba por semejanza de triángulos, que se supone que es la prueba que utilizó Pitágoras. ^{[14] [15]}

Pruebas por disección y reordenamiento

Otra reorganización se da en la animación del medio. Se forma un cuadrado grande con área c ² , a partir de cuatro triángulos rectángulos idénticos con lados a , b y c , ajustados alrededor de un cuadrado central pequeño. Luego se forman dos rectángulos con lados a y b moviendo los triángulos. Combinando el cuadrado más pequeño con estos rectángulos se producen dos cuadrados de áreas a ² y b ² , que deben tener la misma área que el cuadrado grande inicial. ^[16]

La tercera imagen, la de más a la derecha, también da una prueba. Los dos cuadrados superiores están divididos, como se muestra con el sombreado azul y verde, en partes que, al reorganizarse, pueden encajar en el cuadrado inferior sobre la hipotenusa; o, a la inversa, el cuadrado grande puede dividirse, como se muestra, en partes que llenen los otros dos. Esta forma de cortar una figura en partes y reorganizarlas para obtener otra figura se llama disección . Esto demuestra que el área del cuadrado grande es igual a la de los dos más pequeños. ^[17]

Prueba mediante esquila preservando el área

Demostración visual del teorema de Pitágoras mediante cizallamiento que preserva el área

Como se muestra en la animación adjunta, las aplicaciones de corte y las traslaciones que preservan el área pueden transformar los cuadrados de los lados adyacentes al ángulo recto en el cuadrado de la hipotenusa, cubriéndolos juntos de manera exacta. ^[18] Cada corte deja la base y la altura sin cambios, por lo que el área también permanece sin cambios. Las traslaciones también dejan el área sin cambios, ya que no alteran las formas en absoluto. Cada cuadrado primero se corta en un paralelogramo y luego en un rectángulo que se puede trasladar a una sección del cuadrado de la hipotenusa.

Otras pruebas algebraicas

Una prueba relacionada fue publicada por el futuro presidente de los EE. UU. James A. Garfield (en ese entonces representante de los EE. UU. ) (ver diagrama). ^{[19] [20] [21]} En lugar de un cuadrado, utiliza un trapezoide , que se puede construir a partir del cuadrado en la segunda de las pruebas anteriores al dividir a lo largo de una diagonal del cuadrado interior, para dar el trapezoide como se muestra en el diagrama. El área del trapezoide se puede calcular como la mitad del área del cuadrado, es decir

${\displaystyle {\frac {1}{2}}(b+a)^{2}.}$

El cuadrado interior se divide a la mitad de manera similar, y solo hay dos triángulos, por lo que la prueba continúa como se indicó anteriormente, excepto por un factor de , que se elimina al multiplicar por dos para obtener el resultado. ${\displaystyle {\frac {1}{2}}}$

Demostración mediante diferenciales

Se puede llegar al teorema de Pitágoras estudiando cómo los cambios en un lado producen un cambio en la hipotenusa y empleando el cálculo . ^{[22] [23] [24]}

El triángulo ABC es un triángulo rectángulo, como se muestra en la parte superior del diagrama, siendo BC la hipotenusa. Al mismo tiempo, se miden las longitudes de los triángulos como se muestra, siendo la hipotenusa de longitud y , el lado AC de longitud x y el lado AB de longitud a , como se ve en la parte inferior del diagrama.

Diagrama para la prueba diferencial

Si x se incrementa en una pequeña cantidad dx al extender el lado AC ligeramente hasta D , entonces y también aumenta en dy . Estos forman dos lados de un triángulo, CDE , que (con E elegido de modo que CE sea perpendicular a la hipotenusa) es un triángulo rectángulo aproximadamente similar a ABC . Por lo tanto, las razones de sus lados deben ser las mismas, es decir:

${\displaystyle {\frac {dy}{dx}}={\frac {x}{y}}.}$

Esto se puede reescribir como , que es una ecuación diferencial que se puede resolver mediante integración directa: ${\displaystyle y\,dy=x\,dx}$

${\displaystyle \int y\,dy=\int x\,dx\,,}$

donación

${\displaystyle y^{2}=x^{2}+C.}$

La constante se puede deducir de x = 0, y = a para dar la ecuación

${\displaystyle y^{2}=x^{2}+a^{2}.}$

Esta es más una prueba intuitiva que formal: puede hacerse más rigurosa si se utilizan límites adecuados en lugar de dx y dy .

Conversar

El recíproco del teorema también es cierto: ^[25]

Dado un triángulo con lados de longitud a , b y c , si a ² + b ² = c ² , entonces el ángulo entre los lados a y b es un ángulo recto .

Para tres números reales positivos cualesquiera a , b y c tales que a ² + b ² = c ² , existe un triángulo con lados a , b y c como consecuencia del inverso de la desigualdad del triángulo .

Esta recíproca aparece en los Elementos de Euclides (Libro I, Proposición 48): "Si en un triángulo el cuadrado de uno de los lados es igual a la suma de los cuadrados de los dos lados restantes del triángulo, entonces el ángulo contenido por los dos lados restantes del triángulo es recto". ^[26]

Se puede demostrar utilizando la ley de los cosenos o de la siguiente manera:

Sea ABC un triángulo cuyos lados tienen longitudes a , b y c , con a ² + b ² = c ² . Construya un segundo triángulo cuyos lados tengan longitud a y b y que contengan un ángulo recto. Por el teorema de Pitágoras, se deduce que la hipotenusa de este triángulo tiene longitud c = √ a ² + b ² , la misma que la hipotenusa del primer triángulo. Como los lados de ambos triángulos tienen las mismas longitudes a , b y c , los triángulos son congruentes y deben tener los mismos ángulos. Por lo tanto, el ángulo entre los lados de longitud a y b en el triángulo original es un ángulo recto.

La demostración del inverso anterior hace uso del propio teorema de Pitágoras. El inverso también puede demostrarse sin suponer el teorema de Pitágoras. ^{[27] [28]}

Un corolario del inverso del teorema de Pitágoras es un método simple para determinar si un triángulo es rectángulo, obtuso o acutángulo, como sigue. Sea c el más largo de los tres lados y a + b > c (de lo contrario no hay triángulo según la desigualdad del triángulo ). Se aplican las siguientes afirmaciones: ^[29]

• Si a ² + b ² = c ² , entonces el triángulo es rectángulo .
• Si a ² + b ² > c ² , entonces el triángulo es agudo .
• Si a ² + b ² < c ² , entonces el triángulo es obtuso .

Edsger W. Dijkstra ha formulado esta proposición sobre los triángulos agudos, rectángulos y obtusos en este lenguaje:

sgn( α + β − γ ) = sgn( a ² + segundo ² − c ² ),

donde α es el ángulo opuesto al lado a , β es el ángulo opuesto al lado b , γ es el ángulo opuesto al lado c y sgn es la función de signo . ^[30]

Consecuencias y usos del teorema

Ternas pitagóricas

Una terna pitagórica tiene tres números enteros positivos a , b y c , tales que a ² + b ² = c ² . En otras palabras, una terna pitagórica representa las longitudes de los lados de un triángulo rectángulo donde los tres lados tienen longitudes enteras. ^[1] Una terna de este tipo se escribe comúnmente ( a , b , c ). Algunos ejemplos bien conocidos son (3, 4, 5) y (5, 12, 13).

Una terna pitagórica primitiva es aquella en la que a , b y c son coprimos (el máximo común divisor de a , b y c es 1).

La siguiente es una lista de ternas pitagóricas primitivas con valores menores a 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Teorema de Pitágoras inverso

Dado un triángulo rectángulo con lados y altura (una línea desde el ángulo recto y perpendicular a la hipotenusa ), el teorema de Pitágoras tiene, ${\displaystyle a,b,c}$ ${\displaystyle d}$ ${\displaystyle c}$

${\displaystyle a^{2}+b^{2}=c^{2}}$

Mientras que el teorema de Pitágoras inverso relaciona los dos catetos con la altitud , ^[31] ${\displaystyle a,b}$ ${\displaystyle d}$

${\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{d^{2}}}}$

La ecuación se puede transformar a,

${\displaystyle {\frac {1}{(xz)^{2}}}+{\frac {1}{(yz)^{2}}}={\frac {1}{(xy)^{2}}}}$

donde para cualquier real distinto de cero . Si los son enteros , la solución más pequeña es entonces ${\displaystyle x^{2}+y^{2}=z^{2}}$ ${\displaystyle x,y,z}$ ${\displaystyle a,b,d}$ ${\displaystyle a>b>d}$

${\displaystyle {\frac {1}{20^{2}}}+{\frac {1}{15^{2}}}={\frac {1}{12^{2}}}}$

utilizando el triple pitagórico más pequeño . El teorema de Pitágoras recíproco es un caso especial de la ecuación óptica ${\displaystyle 3,4,5}$

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{r}}}$

donde los denominadores son cuadrados y también para un triángulo heptagonal cuyos lados son números cuadrados. ${\displaystyle p,q,r}$

Longitudes inconmensurables

La espiral de Teodoro : una construcción para segmentos de línea con longitudes cuyas razones son la raíz cuadrada de un entero positivo

Una de las consecuencias del teorema de Pitágoras es que los segmentos de recta cuyas longitudes son inconmensurables (por lo que su razón no es un número racional ) se pueden construir utilizando una regla y un compás . El teorema de Pitágoras permite la construcción de longitudes inconmensurables porque la hipotenusa de un triángulo está relacionada con los lados mediante la operación de la raíz cuadrada .

La figura de la derecha muestra cómo construir segmentos de línea cuyas longitudes estén en razón de la raíz cuadrada de cualquier entero positivo. ^[32] Cada triángulo tiene un lado (etiquetado como "1") que es la unidad elegida para la medida. En cada triángulo rectángulo, el teorema de Pitágoras establece la longitud de la hipotenusa en términos de esta unidad. Si una hipotenusa está relacionada con la unidad por la raíz cuadrada de un entero positivo que no es un cuadrado perfecto, es una realización de una longitud inconmensurable con la unidad, como √ 2 , √ 3 , √ 5  . Para más detalles, consulte Irracional cuadrático .

Las longitudes inconmensurables entraban en conflicto con el concepto de la escuela pitagórica de que los números eran únicamente números enteros. La escuela pitagórica trataba las proporciones mediante la comparación de múltiplos enteros de una subunidad común. ^[33] Según una leyenda, Hípaso de Metaponto ( ca. 470 a. C.) se ahogó en el mar por dar a conocer la existencia de lo irracional o inconmensurable. ^[34] Una discusión cuidadosa de las contribuciones de Hípaso se encuentra en Fritz . ^[35]

Números complejos

El valor absoluto de un número complejo z es la distancia r desde z hasta el origen.

Para cualquier número complejo

${\displaystyle z=x+iy,}$

El valor absoluto o módulo viene dado por

${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}$

Así que las tres cantidades, r , x e y están relacionadas por la ecuación de Pitágoras,

${\displaystyle r^{2}=x^{2}+y^{2}.}$

Tenga en cuenta que r se define como un número positivo o cero, pero x e y pueden ser tanto negativos como positivos. Geométricamente, r es la distancia de z desde cero o el origen O en el plano complejo .

Esto se puede generalizar para encontrar la distancia entre dos puntos, por ejemplo z ₁ y z _2. La distancia requerida está dada por

${\displaystyle |z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}},}$

Así que nuevamente están relacionados por una versión de la ecuación pitagórica,

${\displaystyle |z_{1}-z_{2}|^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}.}$

Distancia euclidiana

La fórmula de la distancia en coordenadas cartesianas se deriva del teorema de Pitágoras. ^[36] Si ( x ₁ , y ₁ ) y ( x ₂ , y ₂ ) son puntos en el plano, entonces la distancia entre ellos, también llamada distancia euclidiana , está dada por

${\displaystyle {\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}$

De manera más general, en el espacio n euclidiano , la distancia euclidiana entre dos puntos, y , se define, por generalización del teorema de Pitágoras, como: ${\displaystyle A\,=\,(a_{1},a_{2},\dots ,a_{n})}$ ${\displaystyle B\,=\,(b_{1},b_{2},\dots ,b_{n})}$

${\displaystyle {\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}}}={\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

Si en lugar de la distancia euclidiana se utiliza el cuadrado de este valor (la distancia euclidiana al cuadrado o SED), la ecuación resultante evita las raíces cuadradas y es simplemente una suma de la SED de las coordenadas:

${\displaystyle (a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}=\sum _{i=1}^{n}(a_{i}-b_{i})^{2}.}$

La forma cuadrada es una función suave y convexa de ambos puntos, y se utiliza ampliamente en la teoría de optimización y la estadística , formando la base de los mínimos cuadrados .

Distancia euclidiana en otros sistemas de coordenadas

Si no se utilizan coordenadas cartesianas, por ejemplo, si se utilizan coordenadas polares en dos dimensiones o, en términos más generales, si se utilizan coordenadas curvilíneas , las fórmulas que expresan la distancia euclidiana son más complicadas que el teorema de Pitágoras, pero se pueden derivar de él. Un ejemplo típico en el que la distancia en línea recta entre dos puntos se convierte en coordenadas curvilíneas se puede encontrar en las aplicaciones de los polinomios de Legendre en física . Las fórmulas se pueden descubrir utilizando el teorema de Pitágoras con las ecuaciones que relacionan las coordenadas curvilíneas con las coordenadas cartesianas. Por ejemplo, las coordenadas polares ( r , θ ) se pueden introducir como:

${\displaystyle x=r\cos \theta ,\ y=r\sin \theta .}$

Entonces, dos puntos con ubicaciones ( r ₁ , θ ₁ ) y ( r ₂ , θ ₂ ) están separados por una distancia s :

${\displaystyle s^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}=(r_{1}\cos \theta _{1}-r_{2}\cos \theta _{2})^{2}+(r_{1}\sin \theta _{1}-r_{2}\sin \theta _{2})^{2}.}$

Realizando los cuadrados y combinando términos, la fórmula pitagórica para la distancia en coordenadas cartesianas produce la separación en coordenadas polares como:

${\displaystyle {\begin{aligned}s^{2}&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\left(\cos \theta _{1}\cos \theta _{2}+\sin \theta _{1}\sin \theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left(\theta _{1}-\theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \Delta \theta ,\end{aligned}}}$

utilizando las fórmulas trigonométricas de producto-suma . Esta fórmula es la ley de los cosenos, a veces llamada teorema de Pitágoras generalizado. ^[37] A partir de este resultado, para el caso en que los radios de las dos ubicaciones están en ángulos rectos, el ángulo encerrado Δ θ = π /2, y se recupera la forma correspondiente al teorema de Pitágoras: El teorema de Pitágoras, válido para triángulos rectángulos, es por lo tanto un caso especial de la ley más general de los cosenos, válida para triángulos arbitrarios. ${\displaystyle s^{2}=r_{1}^{2}+r_{2}^{2}.}$

Identidad trigonométrica pitagórica

Triángulos rectángulos semejantes que muestran el seno y el coseno del ángulo θ

En un triángulo rectángulo con lados a , b e hipotenusa c , la trigonometría determina el seno y el coseno del ángulo θ entre el lado a y la hipotenusa como:

${\displaystyle \sin \theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.}$

De lo cual se desprende:

${\displaystyle {\cos }^{2}\theta +{\sin }^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}=1,}$

donde el último paso aplica el teorema de Pitágoras. Esta relación entre seno y coseno a veces se denomina identidad trigonométrica pitagórica fundamental. ^[38] En triángulos semejantes, las razones de los lados son las mismas independientemente del tamaño de los triángulos y dependen de los ángulos. En consecuencia, en la figura, el triángulo con hipotenusa de tamaño unitario tiene un lado opuesto de tamaño sen  θ y un lado adyacente de tamaño cos  θ en unidades de la hipotenusa.

Relación con el producto vectorial

El área de un paralelogramo como producto vectorial; los vectores a y b identifican un plano y a × b es normal a este plano.

El teorema de Pitágoras relaciona el producto vectorial y el producto escalar de manera similar: ^[39]

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}+(\mathbf {a} \cdot \mathbf {b} )^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}.}$

Esto se puede ver en las definiciones del producto vectorial y del producto escalar, como

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=ab\mathbf {n} \sin {\theta }\\\mathbf {a} \cdot \mathbf {b} &=ab\cos {\theta },\end{aligned}}}$

donde n es un vector unitario normal tanto a a como a b . La relación se desprende de estas definiciones y de la identidad trigonométrica pitagórica.

Esto también se puede utilizar para definir el producto vectorial. Reordenando la siguiente ecuación se obtiene

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

Esto puede considerarse como una condición del producto vectorial y, por lo tanto, parte de su definición, por ejemplo en siete dimensiones . ^{[40] [41]}

Como axioma

Si se supone que los cuatro primeros axiomas de la geometría euclidiana son verdaderos, entonces el teorema de Pitágoras es equivalente al quinto. Es decir, el quinto postulado de Euclides implica el teorema de Pitágoras y viceversa.

Generalizaciones

Figuras similares en los tres lados

El teorema de Pitágoras se generaliza más allá de las áreas de los cuadrados de los tres lados a cualquier figura similar . Esto fue conocido por Hipócrates de Quíos en el siglo V a. C., ^[42] y fue incluido por Euclides en sus Elementos : ^[43]

Si se construyen figuras semejantes (ver geometría euclidiana ) con lados correspondientes en los lados de un triángulo rectángulo, entonces la suma de las áreas de las de los dos lados menores es igual al área de la del lado mayor.

Esta extensión supone que los lados del triángulo original son los lados correspondientes de las tres figuras congruentes (por lo que las razones comunes de los lados entre las figuras similares son a:b:c ). ^[44] Si bien la prueba de Euclides solo se aplica a polígonos convexos, el teorema también se aplica a polígonos cóncavos e incluso a figuras similares que tienen límites curvos (pero aún con parte del límite de una figura siendo el lado del triángulo original). ^[44]

La idea básica de esta generalización es que el área de una figura plana es proporcional al cuadrado de cualquier dimensión lineal y, en particular, es proporcional al cuadrado de la longitud de cualquier lado. Por lo tanto, si se construyen figuras similares con áreas A , B y C sobre lados con longitudes correspondientes a , b y c , entonces:

${\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,}$

${\displaystyle \Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,.}$

Pero, por el teorema de Pitágoras, a ² + b ² = c ² , luego A + B = C .

Por el contrario, si podemos demostrar que A + B = C para tres figuras semejantes sin utilizar el teorema de Pitágoras, entonces podemos trabajar a la inversa para construir una prueba del teorema. Por ejemplo, el triángulo central inicial puede replicarse y utilizarse como un triángulo C sobre su hipotenusa, y se pueden construir dos triángulos rectángulos semejantes ( A y B ) sobre los otros dos lados, formados dividiendo el triángulo central por su altura . La suma de las áreas de los dos triángulos más pequeños es, por tanto, la del tercero, por lo que A + B = C y, invirtiendo la lógica anterior, se llega al teorema de Pitágoras a ² + b ² = c ² . ( Véase también la prueba de Einstein por disección sin reordenamiento )

Ley de los cosenos

La separación s de dos puntos (r ₁ , θ ₁ ) y (r ₂ , θ ₂ ) en coordenadas polares viene dada por la ley de los cosenos . Ángulo interior Δθ = θ ₁ −θ ₂ .

El teorema de Pitágoras es un caso especial del teorema más general que relaciona las longitudes de los lados de cualquier triángulo, la ley de los cosenos, que establece que donde es el ángulo entre los lados y . ^[45] $${\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2}}$$ ${\displaystyle \theta }$ ${\displaystyle a}$ ${\displaystyle b}$

Cuando son radianes o 90°, entonces , y la fórmula se reduce al teorema de Pitágoras habitual. ${\displaystyle \theta }$ ${\displaystyle {\frac {\pi }{2}}}$ ${\displaystyle \cos {\theta }=0}$

Triángulo arbitrario

Generalización del teorema de Pitágoras por Tâbit ibn Qorra . ^[46] Panel inferior: reflexión del triángulo CAD (arriba) para formar el triángulo DAC, similar al triángulo ABC (arriba).

En cualquier ángulo seleccionado de un triángulo general de lados a, b, c , inscribe un triángulo isósceles tal que los ángulos iguales en su base θ sean iguales que el ángulo seleccionado. Supón que el ángulo seleccionado θ es opuesto al lado etiquetado c . Al inscribir el triángulo isósceles se forma el triángulo CAD con un ángulo θ opuesto al lado b y con un lado r a lo largo de c . Se forma un segundo triángulo con un ángulo θ opuesto al lado a y un lado con una longitud s a lo largo de c , como se muestra en la figura. Thābit ibn Qurra afirmó que los lados de los tres triángulos estaban relacionados como: ^{[47] [48]}

${\displaystyle a^{2}+b^{2}=c(r+s)\ .}$

A medida que el ángulo θ se acerca a π /2, la base del triángulo isósceles se estrecha y las longitudes r y s se superponen cada vez menos. Cuando θ = π /2, ADB se convierte en un triángulo rectángulo, r + s = c y se recupera el teorema de Pitágoras original.

Una prueba observa que el triángulo ABC tiene los mismos ángulos que el triángulo CAD , pero en orden opuesto. (Los dos triángulos comparten el ángulo en el vértice A, ambos contienen el ángulo θ y, por lo tanto, también tienen el mismo tercer ángulo según el postulado del triángulo ). En consecuencia, ABC es similar al reflejo de CAD , el triángulo DAC en el panel inferior. Tomando la relación de los lados opuestos y adyacentes a θ,

${\displaystyle {\frac {c}{b}}={\frac {b}{r}}\ .}$

De la misma manera, para el reflejo del otro triángulo,

${\displaystyle {\frac {c}{a}}={\frac {a}{s}}\ .}$

Despejando fracciones y sumando estas dos relaciones:

${\displaystyle cs+cr=a^{2}+b^{2}\ ,}$

El resultado requerido.

El teorema sigue siendo válido si el ángulo es obtuso, por lo que las longitudes r y s no se superponen. ${\displaystyle \theta }$

Triángulos generales utilizando paralelogramos

Generalización para triángulos arbitrarios, área
verde = área azul

Construcción para la demostración de la generalización del paralelogramo

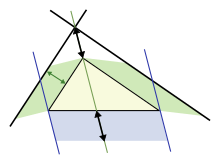
El teorema del área de Pappus es una generalización adicional que se aplica a triángulos que no son rectángulos, utilizando paralelogramos en los tres lados en lugar de cuadrados (los cuadrados son un caso especial, por supuesto). La figura superior muestra que para un triángulo escaleno, el área del paralelogramo del lado más largo es la suma de las áreas de los paralelogramos de los otros dos lados, siempre que el paralelogramo del lado más largo se construya como se indica (las dimensiones etiquetadas con flechas son las mismas y determinan los lados del paralelogramo inferior). Esta sustitución de cuadrados por paralelogramos tiene un claro parecido con el teorema de Pitágoras original, y fue considerada una generalización por Pappus de Alejandría en el año 4 d. C. ^{[49] [50]}

La figura inferior muestra los elementos de la prueba. Concéntrese en el lado izquierdo de la figura. El paralelogramo verde izquierdo tiene la misma área que la porción azul izquierda del paralelogramo inferior porque ambos tienen la misma base b y altura h . Sin embargo, el paralelogramo verde izquierdo también tiene la misma área que el paralelogramo verde izquierdo de la figura superior, porque tienen la misma base (el lado superior izquierdo del triángulo) y la misma altura normal a ese lado del triángulo. Repitiendo el argumento para el lado derecho de la figura, el paralelogramo inferior tiene la misma área que la suma de los dos paralelogramos verdes.

Geometría sólida

El teorema de Pitágoras en tres dimensiones relaciona la diagonal AD con los tres lados.

Un tetraedro con un ángulo recto que mira hacia afuera.

En términos de geometría de sólidos , el teorema de Pitágoras se puede aplicar a tres dimensiones de la siguiente manera. Considere el cuboide que se muestra en la figura. La longitud de la diagonal de la cara AC se obtiene a partir del teorema de Pitágoras como:

${\displaystyle {\overline {AC}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BC}}^{\,2}\,,}$

donde estos tres lados forman un triángulo rectángulo. Utilizando la diagonal AC y la arista horizontal CD , la longitud de la diagonal del cuerpo AD se obtiene mediante una segunda aplicación del teorema de Pitágoras como:

${\displaystyle {\overline {AD}}^{\,2}={\overline {AC}}^{\,2}+{\overline {CD}}^{\,2}\,,}$

o hacerlo todo en un solo paso:

${\displaystyle {\overline {AD}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BC}}^{\,2}+{\overline {CD}}^{\,2}\,.}$

Este resultado es la expresión tridimensional de la magnitud de un vector v (la diagonal AD) en términos de sus componentes ortogonales { v _k } (los tres lados mutuamente perpendiculares):

${\displaystyle \|\mathbf {v} \|^{2}=\sum _{k=1}^{3}\|\mathbf {v} _{k}\|^{2}.}$

Esta formulación de un solo paso puede considerarse una generalización del teorema de Pitágoras a dimensiones superiores. Sin embargo, este resultado es en realidad solo la aplicación repetida del teorema de Pitágoras original a una sucesión de triángulos rectángulos en una secuencia de planos ortogonales.

Una generalización sustancial del teorema de Pitágoras a tres dimensiones es el teorema de De Gua , llamado así por Jean Paul de Gua de Malves : Si un tetraedro tiene una esquina en ángulo recto (como una esquina de un cubo ), entonces el cuadrado del área de la cara opuesta a la esquina en ángulo recto es la suma de los cuadrados de las áreas de las otras tres caras. Este resultado se puede generalizar como en el " teorema de Pitágoras n -dimensional": ^[51]

Sean vectores ortogonales en R ⁿ . Considérese el símplex n -dimensional S con vértices . (Piense en el símplex ( n  − 1)-dimensional con vértices que no incluyen el origen como la "hipotenusa" de S y las caras ( n  − 1)-dimensionales restantes de S como sus "catetos".) Entonces el cuadrado del volumen de la hipotenusa de S es la suma de los cuadrados de los volúmenes de los n catetos. ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ ${\displaystyle 0,x_{1},\ldots ,x_{n}}$ ${\displaystyle x_{1},\ldots ,x_{n}}$

Esta afirmación se ilustra en tres dimensiones con el tetraedro de la figura. La "hipotenusa" es la base del tetraedro que se encuentra en la parte posterior de la figura, y los "catetos" son los tres lados que emanan del vértice que se encuentra en primer plano. A medida que aumenta la profundidad de la base desde el vértice, aumenta el área de los "catetos", mientras que la de la base permanece fija. El teorema sugiere que cuando esta profundidad está en el valor que crea un vértice recto, se aplica la generalización del teorema de Pitágoras. En una redacción diferente: ^[52]

Dado un símplex n -rectangular y n -dimensional, el cuadrado del contenido ( n  − 1) de la faceta opuesta al vértice derecho será igual a la suma de los cuadrados de los contenidos ( n  − 1) de las facetas restantes.

Espacios interiores de productos

Vectores que intervienen en la ley del paralelogramo

El teorema de Pitágoras se puede generalizar a los espacios de producto interno , ^{[53] que son generalizaciones de los} espacios euclidianos bidimensionales y tridimensionales conocidos . Por ejemplo, una función puede considerarse como un vector con infinitos componentes en un espacio de producto interno, como en el análisis funcional . ^[54]

En un espacio de producto interno, el concepto de perpendicularidad se reemplaza por el concepto de ortogonalidad : dos vectores v y w son ortogonales si su producto interno es cero. El producto interno es una generalización del producto escalar de vectores. El producto escalar se denomina producto interno estándar o producto interno euclidiano . Sin embargo, son posibles otros productos internos. ^[55] ${\displaystyle \langle \mathbf {v} ,\mathbf {w} \rangle }$

El concepto de longitud se sustituye por el concepto de norma ‖ v ‖ de un vector v , definido como: ^[56]

${\displaystyle \lVert \mathbf {v} \rVert \equiv {\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}\,.}$

En un espacio de producto interno, el teorema de Pitágoras establece que para dos vectores ortogonales v y w tenemos

${\displaystyle \left\|\mathbf {v} +\mathbf {w} \right\|^{2}=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2}.}$

Aquí los vectores v y w son similares a los lados de un triángulo rectángulo con hipotenusa dada por la suma vectorial v  +  w . Esta forma del teorema de Pitágoras es una consecuencia de las propiedades del producto interno :

${\displaystyle {\begin{aligned}\left\|\mathbf {v} +\mathbf {w} \right\|^{2}&=\langle \mathbf {v+w} ,\ \mathbf {v+w} \rangle \\[3mu]&=\langle \mathbf {v} ,\ \mathbf {v} \rangle +\langle \mathbf {w} ,\ \mathbf {w} \rangle +\langle \mathbf {v,\ w} \rangle +\langle \mathbf {w,\ v} \rangle \\[3mu]&=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2},\end{aligned}}}$

donde debido a la ortogonalidad. ${\displaystyle \langle \mathbf {v,\ w} \rangle =\langle \mathbf {w,\ v} \rangle =0}$

Una generalización adicional del teorema de Pitágoras en un espacio de producto interno a vectores no ortogonales es la ley del paralelogramo : ^[56]

${\displaystyle 2\|\mathbf {v} \|^{2}+2\|\mathbf {w} \|^{2}=\|\mathbf {v+w} \|^{2}+\|\mathbf {v-w} \|^{2}\ ,}$

que dice que el doble de la suma de los cuadrados de las longitudes de los lados de un paralelogramo es la suma de los cuadrados de las longitudes de las diagonales. Cualquier norma que satisfaga esta igualdad es ipso facto una norma correspondiente a un producto interno. ^[56]

La identidad de Pitágoras se puede extender a sumas de más de dos vectores ortogonales. Si v ₁ , v ₂ , ..., v _n son vectores ortogonales por pares en un espacio de producto interno, entonces la aplicación del teorema de Pitágoras a pares sucesivos de estos vectores (como se describe para 3 dimensiones en la sección sobre geometría de sólidos) da como resultado la ecuación ^[57]

${\displaystyle {\biggl \|}\sum _{k=1}^{n}\mathbf {v} _{k}{\biggr \|}^{2}=\sum _{k=1}^{n}\|\mathbf {v} _{k}\|^{2}}$

Conjuntos demetro-objetos dimensionales ennorte-espacio dimensional

Otra generalización del teorema de Pitágoras se aplica a conjuntos de objetos medibles según el método de Lebesgue en cualquier número de dimensiones. En concreto, el cuadrado de la medida de un conjunto de objetos de dimensión m en uno o más planos paralelos de dimensión m en un espacio euclidiano de dimensión n es igual a la suma de los cuadrados de las medidas de las proyecciones ortogonales de los objetos sobre todos los subespacios de coordenadas de dimensión m . ^[58]

En términos matemáticos:

${\displaystyle \mu _{ms}^{2}=\sum _{i=1}^{x}\mathbf {\mu ^{2}} _{mp_{i}}}$

dónde:

• ${\displaystyle \mu _{m}}$es una medida en m -dimensiones (una longitud en una dimensión, un área en dos dimensiones, un volumen en tres dimensiones, etc.).
• ${\displaystyle s}$es un conjunto de uno o más objetos m -dimensionales no superpuestos en uno o más planos m -dimensionales paralelos en el espacio euclidiano n -dimensional.
• ${\displaystyle \mu _{ms}}$es la medida total (suma) del conjunto de objetos m -dimensionales.
• ${\displaystyle p}$representa una proyección m -dimensional del conjunto original sobre un subespacio de coordenadas ortogonales.
• ${\displaystyle \mu _{mp_{i}}}$es la medida de la proyección del conjunto m -dimensional sobre un subespacio de coordenadas m -dimensional . Debido a que las proyecciones de objetos pueden superponerse en un subespacio de coordenadas, la medida de cada proyección de objeto en el conjunto debe calcularse individualmente y luego las medidas de todas las proyecciones deben sumarse para proporcionar la medida total para el conjunto de proyecciones en el subespacio de coordenadas dado. ${\displaystyle i}$
• ${\displaystyle x}$es el número de subespacios de coordenadas ortogonales de dimensión m en el espacio de dimensión n ( R ⁿ ) sobre los que se proyectan los objetos de dimensión m ( m ≤ n ): $${\displaystyle x={\binom {n}{m}}={\frac {n!}{m!(n-m)!}}}$$

Geometría no euclidiana

El teorema de Pitágoras se deriva de los axiomas de la geometría euclidiana y, de hecho, si el teorema de Pitágoras fallara para algún triángulo rectángulo, entonces el plano en el que está contenido este triángulo no puede ser euclidiano. Más precisamente, el teorema de Pitágoras implica, y es implicado por, el Postulado de las Paralelas (Quinto) de Euclides . ^{[59] [60]} Por lo tanto, los triángulos rectángulos en una geometría no euclidiana ^[61] no satisfacen el teorema de Pitágoras. Por ejemplo, en geometría esférica , los tres lados del triángulo rectángulo (digamos a , b y c ) que delimita un octante de la esfera unidad tienen una longitud igual a π /2, y todos sus ángulos son ángulos rectos, lo que viola el teorema de Pitágoras porque . ${\displaystyle a^{2}+b^{2}=2c^{2}>c^{2}}$

Aquí se consideran dos casos de geometría no euclidiana: la geometría esférica y la geometría del plano hiperbólico ; en cada caso, como en el caso euclidiano para triángulos no rectángulos, el resultado que reemplaza al teorema de Pitágoras se sigue de la ley apropiada de los cosenos.

Sin embargo, el teorema de Pitágoras sigue siendo válido en la geometría hiperbólica y la geometría elíptica si la condición de que el triángulo sea rectángulo se reemplaza por la condición de que dos de los ángulos sumen el tercero, digamos A + B = C. Los lados se relacionan entonces de la siguiente manera: la suma de las áreas de los círculos con diámetros a y b es igual al área del círculo con diámetro c . ^[62]

Geometría esférica

Triángulo esférico

Para cualquier triángulo rectángulo sobre una esfera de radio R (por ejemplo, si γ en la figura es un ángulo recto), con lados a , b , c , la relación entre los lados toma la forma: ^[63]

${\displaystyle \cos {\frac {c}{R}}=\cos {\frac {a}{R}}\,\cos {\frac {b}{R}}.}$

Esta ecuación puede derivarse como un caso especial de la ley esférica de los cosenos que se aplica a todos los triángulos esféricos:

${\displaystyle \cos {\frac {c}{R}}=\cos {\frac {a}{R}}\,\cos {\frac {b}{R}}+\sin {\frac {a}{R}}\,\sin {\frac {b}{R}}\,\cos {\gamma }.}$

Para triángulos infinitesimales en la esfera (o equivalentemente, para triángulos esféricos finitos en una esfera de radio infinito), la relación esférica entre los lados de un triángulo rectángulo se reduce a la forma euclidiana del teorema de Pitágoras. Para ver cómo, supongamos que tenemos un triángulo esférico de longitudes de lado fijas a , b y c en una esfera con radio en expansión R . A medida que R se acerca al infinito, las cantidades a/R , b/R y c /R tienden a cero y la identidad pitagórica esférica se reduce a , por lo que debemos observar su expansión asintótica . ${\displaystyle 1=1,}$

La serie de Maclaurin para la función coseno se puede escribir como con el término restante en notación O mayúscula . Si se deja que sea un lado del triángulo y se trata la expresión como una expansión asintótica en términos de R para un c fijo , ${\textstyle \cos x=1-{\tfrac {1}{2}}x^{2}+O{\left(x^{4}\right)}}$ ${\displaystyle x=c/R}$

${\displaystyle {\begin{aligned}\cos {\frac {c}{R}}=1-{\frac {c^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}\end{aligned}}}$

y lo mismo para a y b . Sustituyendo la expansión asintótica para cada uno de los cosenos en la relación esférica para un triángulo rectángulo se obtiene

${\displaystyle {\begin{aligned}1-{\frac {c^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}&=\left(1-{\frac {a^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}\right)\left(1-{\frac {b^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}\right)\\&=1-{\frac {a^{2}}{2R^{2}}}-{\frac {b^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}.\end{aligned}}}$

Restando 1 y luego negando cada lado,

${\displaystyle {\frac {c^{2}}{2R^{2}}}={\frac {a^{2}}{2R^{2}}}+{\frac {b^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}.}$

Multiplicando por 2 R ² , la expansión asintótica para c en términos de a , b fijos y la variable R es

${\displaystyle c^{2}=a^{2}+b^{2}+O{\left(R^{-2}\right)}.}$

La relación pitagórica euclidiana se recupera en el límite, ya que el resto se desvanece cuando el radio R se acerca al infinito. ${\textstyle c^{2}=a^{2}+b^{2}}$

Para el cálculo práctico de trigonometría esférica con triángulos rectángulos pequeños, los cosenos se pueden reemplazar por senos utilizando la identidad del ángulo doble para evitar la pérdida de significancia . Entonces, el teorema de Pitágoras esférico se puede escribir alternativamente como ${\displaystyle \cos {2\theta }=1-2\sin ^{2}{\theta }}$

${\displaystyle \sin ^{2}{\frac {c}{2R}}=\sin ^{2}{\frac {a}{2R}}+\sin ^{2}{\frac {b}{2R}}-2\sin ^{2}{\frac {a}{2R}}\,\sin ^{2}{\frac {b}{2R}}.}$

Geometría hiperbólica

Triángulo hiperbólico

En un espacio hiperbólico con curvatura gaussiana uniforme −1/ R ² , para un triángulo rectángulo con catetos a , b , e hipotenusa c , la relación entre los lados toma la forma: ^[64]

${\displaystyle \cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\,\cosh {\frac {b}{R}}}$

donde cosh es el coseno hiperbólico . Esta fórmula es una forma especial de la ley hiperbólica de los cosenos que se aplica a todos los triángulos hiperbólicos: ^[65]

${\displaystyle \cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\ \cosh {\frac {b}{R}}-\sinh {\frac {a}{R}}\ \sinh {\frac {b}{R}}\ \cos \gamma \ ,}$

siendo γ el ángulo en el vértice opuesto al lado c .

Al utilizar la serie de Maclaurin para el coseno hiperbólico, cosh x ≈ 1 + x ² /2 , se puede demostrar que a medida que un triángulo hiperbólico se vuelve muy pequeño (es decir, cuando a , b y c se acercan a cero), la relación hiperbólica para un triángulo rectángulo se aproxima a la forma del teorema de Pitágoras.

Para triángulos rectángulos pequeños ( a , b << R ), los cosenos hiperbólicos se pueden eliminar para evitar la pérdida de significancia , obteniendo

${\displaystyle \sinh ^{2}{\frac {c}{2R}}=\sinh ^{2}{\frac {a}{2R}}+\sinh ^{2}{\frac {b}{2R}}+2\sinh ^{2}{\frac {a}{2R}}\sinh ^{2}{\frac {b}{2R}}\,.}$

Triángulos muy pequeños

Para cualquier curvatura uniforme K (positiva, cero o negativa), en triángulos rectángulos muy pequeños (| K | a ² , | K | b ² << 1) con hipotenusa c , se puede demostrar que

${\displaystyle c^{2}=a^{2}+b^{2}-{\frac {K}{3}}a^{2}b^{2}-{\frac {K^{2}}{45}}a^{2}b^{2}(a^{2}+b^{2})-{\frac {2K^{3}}{945}}a^{2}b^{2}(a^{2}-b^{2})^{2}+O(K^{4}c^{10})\,.}$

Geometría diferencial

Distancia entre puntos separados infinitesimalmente en coordenadas cartesianas (arriba) y coordenadas polares (abajo), según lo indica el teorema de Pitágoras

El teorema de Pitágoras se aplica a los triángulos infinitesimales que se observan en la geometría diferencial . En el espacio tridimensional, la distancia entre dos puntos separados infinitesimalmente satisface

${\displaystyle ds^{2}=dx^{2}+dy^{2}+dz^{2},}$

donde ds es el elemento de distancia y ( dx , dy , dz ) son los componentes del vector que separa los dos puntos. Un espacio de este tipo se denomina espacio euclidiano . Sin embargo, en geometría de Riemann , una generalización de esta expresión útil para coordenadas generales (no solo cartesianas) y espacios generales (no solo euclidianos) toma la forma: ^[66]

${\displaystyle ds^{2}=\sum _{i,j}^{n}g_{ij}\,dx_{i}\,dx_{j}}$

que se denomina tensor métrico . (A veces, por abuso del lenguaje, se aplica el mismo término al conjunto de coeficientes g _ij .) Puede ser una función de la posición y, a menudo, describe el espacio curvo . Un ejemplo sencillo es el espacio euclidiano (plano) expresado en coordenadas curvilíneas . Por ejemplo, en coordenadas polares :

${\displaystyle ds^{2}=dr^{2}+r^{2}d\theta ^{2}\ .}$

Historia

La tablilla Plimpton 322 registra ternas pitagóricas de la época babilónica . ^[67]

Existe un debate sobre si el teorema de Pitágoras fue descubierto una vez, o muchas veces en muchos lugares, y la fecha del primer descubrimiento es incierta, al igual que la fecha de la primera prueba. Los historiadores de las matemáticas mesopotámicas han concluido que la regla pitagórica era de uso generalizado durante el período babilónico antiguo (siglos XX al XVI a. C.), más de mil años antes de que naciera Pitágoras . ^{[68] [69] [70] [71]} La historia del teorema se puede dividir en cuatro partes: conocimiento de las ternas pitagóricas , conocimiento de la relación entre los lados de un triángulo rectángulo, conocimiento de las relaciones entre ángulos adyacentes y pruebas del teorema dentro de algún sistema deductivo .

Escrito alrededor del año 1800  a. C., el Papiro de Berlín 6619 del Imperio Medio egipcio incluye un problema cuya solución es la terna pitagórica 6:8:10, pero el problema no menciona ningún triángulo. La tablilla mesopotámica Plimpton 322 , escrita cerca de Larsa también alrededor del año 1800 a. C., contiene muchas entradas estrechamente relacionadas con las ternas pitagóricas. ^[72]  

En la India , el Baudhayana Shulba Sutra , cuyas fechas se dan de forma variada entre el siglo VIII y el V a.C., ^[73] contiene una lista de ternas pitagóricas y un enunciado del teorema de Pitágoras, tanto en el caso especial del triángulo rectángulo isósceles como en el caso general, al igual que el Apastamba Shulba Sutra ( c.  600 a.C. ). ^[a]

El filósofo y matemático neoplatónico bizantino Proclo , escribiendo en el siglo V d. C., establece dos reglas aritméticas, "una de ellas atribuida a Platón , la otra a Pitágoras", ^[76] para generar ternas pitagóricas especiales. La regla atribuida a Pitágoras ( c.  570  – c.  495 a. C. ) comienza a partir de un número impar y produce una terna con cateto e hipotenusa que difieren en una unidad; la regla atribuida a Platón (428/427 o 424/423 – 348/347 a. C.) comienza a partir de un número par y produce una terna con cateto e hipotenusa que difieren en dos unidades. Según Thomas L. Heath (1861–1940), no existe ninguna atribución específica del teorema a Pitágoras en la literatura griega sobreviviente de los cinco siglos posteriores a la vida de Pitágoras. ^[77] Sin embargo, cuando autores como Plutarco y Cicerón atribuyeron el teorema a Pitágoras, lo hicieron de una manera que sugiere que la atribución era ampliamente conocida e indudable. ^{[78] [79]} El clasicista Kurt von Fritz escribió: "Ya sea que esta fórmula se atribuya correctamente a Pitágoras personalmente... uno puede asumir con seguridad que pertenece al período más antiguo de las matemáticas pitagóricas ". ^[35] Alrededor del 300 a. C., en los Elementos de Euclides, se presenta la prueba axiomática existente más antigua del teorema. ^[80]

Demostración geométrica del teorema de Pitágoras a partir del Zhoubi Suanjing

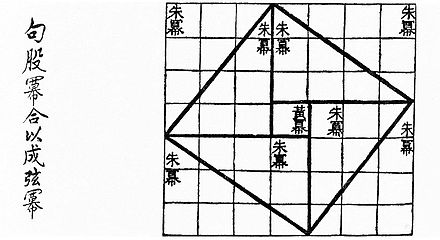
Con contenidos conocidos mucho antes, pero en textos supervivientes que datan aproximadamente del siglo I a.C., el texto chino Zhoubi Suanjing (周髀算经), ( El clásico aritmético del gnomon y los caminos circulares del cielo ) da un razonamiento para el teorema de Pitágoras para el triángulo (3, 4, 5) —en China se le llama " teorema de Gougu " (勾股定理). ^{[81] [82]} Durante la dinastía Han (202 a.C. a 220 d.C.), las ternas pitagóricas aparecen en Los nueve capítulos sobre el arte matemático , ^[83] junto con una mención a los triángulos rectángulos. ^[84] Algunos creen que el teorema surgió por primera vez en China en el siglo XI a. C., ^[85] donde se lo conoce alternativamente como el " teorema de Shang Gao " (商高定理), ^[86] llamado así por el astrónomo y matemático del duque de Zhou , cuyo razonamiento compuso la mayor parte de lo que estaba en el Zhoubi Suanjing . ^[87]

Véase también

• Portal de matemáticas

• Suma en cuadratura
• En Dulcarnon
• Teorema de la bandera británica
• Silla de la novia
• El último teorema de Fermat
• Prueba de Garfield del teorema de Pitágoras
• Hsuan thu
• Teorema de Pitágoras inverso
• Triángulo de Kepler
• Álgebra lineal
• Lista de temas relacionados con los triángulos
• Espacio L ^p
• Número no hipotenusa
• Ley del paralelogramo
• La identidad de Parseval
• Teorema de Ptolomeo
• Pitágoras en la cultura popular
• Expectativa pitagórica
• Teselación pitagórica
• Trigonometría racional en el teorema de Pitágoras
• Teorema de Tales

Notas y referencias

Notas

1. Van der Waerden creía que este material "se basaba sin duda en tradiciones anteriores". ^[74] Carl Boyer afirma que el teorema de Pitágoras del Śulba-sũtram puede haber sido influenciado por las matemáticas mesopotámicas antiguas, pero no hay evidencia concluyente a favor o en contra de esta posibilidad. ^[75]

Referencias

1. Judith D. Sally; Paul Sally (2007). "Capítulo 3: Ternas pitagóricas". De las raíces a la investigación: un desarrollo vertical de problemas matemáticos . Librería de la American Mathematical Society. pág. 63. ISBN 978-0-8218-4403-8.
2. Benson, Donald. El momento de la prueba: epifanías matemáticas , págs. 172-173 (Oxford University Press, 1999).
3. Euclides (1956), págs. 351–352
4. Huffman, Carl (23 de febrero de 2005). "Pitágoras". En Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (edición de invierno de 2018) ."Ahora debería quedar claro que las decisiones sobre las fuentes son cruciales para abordar la cuestión de si Pitágoras era un matemático y un científico. La visión del cosmos de Pitágoras esbozada en los primeros cinco párrafos de esta sección, según la cual no era ni un matemático ni un científico, sigue siendo el consenso".
5. Alexander Bogomolny. "Cut-the-knot.org: Teorema de Pitágoras y sus numerosas demostraciones, Demostración n.° 4". Cut the Knot . Consultado el 4 de noviembre de 2010 .
6. Alexander Bogomolny. "Cut-the-knot.org: Teorema de Pitágoras y sus numerosas demostraciones, Demostración n.° 3". Cut the Knot . Consultado el 4 de noviembre de 2010 .
7. (Loomis 1940)
8. (Maor 2007, pág. 39)
9. Schroeder, Manfred Robert (2012). Fractales, caos, leyes de potencia: minutos de un paraíso infinito . Courier Corporation. págs. 3-4. ISBN 978-0486134789.
10. Véase, por ejemplo, el teorema de Pitágoras por mapeo de corte Archivado el 14 de octubre de 2016 en Wayback Machine , sitio web de la Universidad de Saint Louis Subprograma Java
11. Jan Gullberg (1997). Matemáticas: desde el nacimiento de los números . WW Norton & Company. pág. 435. ISBN 0-393-04002-X.
12. Heiberg, JL "Elementos de geometría de Euclides" (PDF) . págs. 46–47.
13. "Elementos de Euclides, Libro I, Proposición 47".Véase también una versión de página web que utiliza applets Java del Prof. David E. Joyce, de la Universidad Clark.
14. Stephen W. Hawking (2005). Dios creó los números enteros: los avances matemáticos que cambiaron la historia. Filadelfia: Running Press Book Publishers. pág. 12. ISBN 0-7624-1922-9.Esta prueba apareció por primera vez después de que se creó un programa de computadora para verificar pruebas euclidianas.
15. La prueba de Pitágoras probablemente no fue general, ya que la teoría de proporciones se desarrolló sólo dos siglos después de Pitágoras; véase (Maor 2007, p. 25)
16. Alexander Bogomolny . «Teorema de Pitágoras, prueba número 10». Cut the Knot . Consultado el 27 de febrero de 2010 .
17. (Loomis 1940, p. 113, Prueba geométrica 22 y Figura 123)
18. Polster, Burkard (2004). QED: belleza en la demostración matemática . Walker Publishing Company. pág. 49.
19. Publicado en una columna semanal de matemáticas: James A Garfield (1876). "Pons Asinorum". The New England Journal of Education . 3 (14): 161.como se señala en William Dunham (1997). El universo matemático: un viaje alfabético a través de las grandes pruebas, problemas y personalidades. Wiley. p. 96. ISBN 0-471-17661-3.y en Un calendario de fechas matemáticas: 1 de abril de 1876 Archivado el 14 de julio de 2010 en Wayback Machine por V. Frederick Rickey
20. Lantz, David. «Demostración del teorema de Pitágoras según Garfield». Math.Colgate.edu . Archivado desde el original el 28 de agosto de 2013. Consultado el 14 de enero de 2018 .
21. Maor, Eli, El teorema de Pitágoras , Princeton University Press, 2007: págs. 106-107.
22. Mike Staring (1996). "La proposición pitagórica: una prueba por medio del cálculo". Revista de Matemáticas . 69 (1). Asociación Matemática de América: 45–46. doi :10.2307/2691395. JSTOR  2691395.
23. Bogomolny, Alexander. "Teorema de Pitágoras". Miscelánea y acertijos matemáticos interactivos . Alexander Bogomolny. Archivado desde el original el 6 de julio de 2010. Consultado el 9 de mayo de 2010 .
24. Bruce C. Berndt (1988). "Ramanujan: ¿100 años de antigüedad (moderno) o 100 años de modernidad (moderno)?". The Mathematical Intelligencer . 10 (3): 24–31. doi :10.1007/BF03026638. S2CID  123311054.
25. Judith D. Sally; Paul J. Sally Jr. (21 de diciembre de 2007). "Teorema 2.4 (Inverso del teorema de Pitágoras)". Roots to Research . American Mathematical Society . págs. 54–55. ISBN 978-0-8218-4403-8.
26. Elementos de Euclides, Libro I, Proposición 48 De la página web de DE Joyce en la Universidad Clark
27. Casey, Stephen, "El recíproco del teorema de Pitágoras", Mathematical Gazette 92, julio de 2008, 309–313.
28. Mitchell, Douglas W., "Comentarios sobre 92.47", Mathematical Gazette 93, marzo de 2009, 156.
29. Ernest Julius Wilczynski; Herbert Ellsworth Slaught (1914). "Teorema 1 y Teorema 2". Trigonometría plana y aplicaciones. Allyn y Bacon. pág. 85.
30. Dijkstra, Edsger W. (7 de septiembre de 1986). "Sobre el teorema de Pitágoras". EWD975 . Archivo EW Dijkstra.
31. Alexander Bogomolny, Teorema de Pitágoras para los recíprocos, https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
32. Law, Henry (1853). "Corolario 5 de la Proposición XLVII (Teorema de Pitágoras)". Los elementos de Euclides: con muchas proposiciones adicionales y notas explicativas, a las que se añade un ensayo introductorio sobre lógica . John Weale. pág. 49.
33. Shaughan Lavine (1994). Entendiendo el infinito. Harvard University Press. p. 13. ISBN 0-674-92096-1.
34. (Heath 1921, vol. I, págs. 65); Hippasus se encontraba en un viaje en ese momento y sus compañeros lo arrojaron por la borda. Véase James R. Choike (1980). "El pentagrama y el descubrimiento de un número irracional". The College Mathematics Journal . 11 : 312–316.
35. Kurt Von Fritz (abril de 1945). "El descubrimiento de la inconmensurabilidad por Hípaso de Metaponto". Anales de Matemáticas . Segunda serie. 46 (2): 242–264. doi :10.2307/1969021. JSTOR  1969021.
36. Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). "Distancia euclidiana". Dominando algoritmos con Perl . O'Reilly Media, Inc. pág. 426. ISBN 1-56592-398-7.
37. Wentworth, George (2009). Trigonometría plana y tablas. BiblioBazaar, LLC. pág. 116. ISBN 978-1-103-07998-8., Ejercicios, página 116
38. Lawrence S. Leff (2005). PreCalculus the Easy Way (7.ª ed.). Serie educativa de Barron. pág. 296. ISBN 0-7641-2892-2.
39. WS Massey (diciembre de 1983). "Productos cruzados de vectores en espacios euclidianos de dimensiones superiores" (PDF) . The American Mathematical Monthly . 90 (10). Asociación Matemática de América: 697–701. doi :10.2307/2323537. JSTOR  2323537. S2CID  43318100. Archivado desde el original (PDF) el 26 de febrero de 2021.
40. Pertti Lounesto (2001). "§7.4 Producto vectorial de dos vectores". Álgebras y espinores de Clifford (2.ª ed.). Cambridge University Press. pág. 96. ISBN 0-521-00551-5.
41. Francis Begnaud Hildebrand (1992). Métodos de matemáticas aplicadas (Reimpresión de Prentice-Hall 1965 2.ª ed.). Courier Dover Publications. pág. 24. ISBN 0-486-67002-3.
42. Heath, TL, Una historia de las matemáticas griegas , Oxford University Press, 1921; reimpreso por Dover, 1981.
43. Elementos de Euclides : Libro VI, Proposición VI 31: "En los triángulos rectángulos, la figura del lado que subtiende el ángulo recto es igual a las figuras similares y descritas de manera similar en los lados que contienen el ángulo recto".
44. Putz, John F. y Sipka, Timothy A. "Sobre la generalización del teorema de Pitágoras", The College Mathematics Journal 34 (4), septiembre de 2003, págs. 291–295.
45. Lawrence S. Leff (1 de mayo de 2005). Obra citada. Barron's Educational Series. pág. 326. ISBN 0-7641-2892-2.
46. Howard Whitley Eves (1983). "§4.8:...generalización del teorema de Pitágoras". Grandes momentos de la matemática (antes de 1650) . Asociación Matemática de América. pág. 41. ISBN 0-88385-310-8.
47. Aydin Sayili (marzo de 1960). "Generalización del teorema de Pitágoras de Thâbit ibn Qurra". Isis . 51 (1): 35–37. doi :10.1086/348837. JSTOR  227603. S2CID  119868978.
48. Judith D. Sally; Paul Sally (21 de diciembre de 2007). "Ejercicio 2.10 (ii)". De las raíces a la investigación: un desarrollo vertical de problemas matemáticos . American Mathematical Soc. pág. 62. ISBN 978-0-8218-4403-8.
49. Para conocer los detalles de esta construcción, véase Jennings, George (1997). "Figura 1.32: El teorema de Pitágoras generalizado". Geometría moderna con aplicaciones: con 150 figuras (3.ª ed.). Springer. pág. 23. ISBN 0-387-94222-X.
50. Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics . MAA, 2010, ISBN 9780883853481 , pp. 77–78 ( extracto , p. 77, en Google Books ) 
51. Rajendra Bhatia (1997). Análisis matricial. Springer. pág. 21. ISBN 0-387-94846-5.
52. Para una discusión más extensa de esta generalización, véase, por ejemplo, Willie W. Wong Archivado el 29 de diciembre de 2009 en Wayback Machine 2002, Un teorema de Pitágoras n-dimensional generalizado .
53. Fernando van der Heijden; Dick de Ridder (2004). Clasificación, estimación de parámetros y estimación de estado. Wiley. pag. 357.ISBN​ 0-470-09013-8.
54. Qun Lin; Jiafu Lin (2006). Métodos de elementos finitos: precisión y mejora. Elsevier. p. 23. ISBN 7-03-016656-6.
55. Howard Anton; Chris Rorres (2010). Álgebra lineal elemental: versión de aplicaciones (10.ª ed.). Wiley. pág. 336. ISBN 978-0-470-43205-1.
56. Karen Saxe (2002). "Teorema 1.2". Introducción al análisis funcional . Springer. pág. 7. ISBN 0-387-95224-1.
57. Douglas, Ronald G. (1998). Técnicas de álgebra de Banach en teoría de operadores (2.ª ed.). Nueva York, Nueva York: Springer-Verlag New York, Inc., págs. 60-61. ISBN 978-0-387-98377-6.
58. Donald R Conant y William A Beyer (marzo de 1974). "Teorema de Pitágoras generalizado". The American Mathematical Monthly . 81 (3). Asociación Matemática de Estados Unidos: 262–265. doi :10.2307/2319528. JSTOR  2319528.
59. Eric W. Weisstein (2003). Enciclopedia concisa de matemáticas del CRC (2.ª edición). CRC Press. pág. 2147. ISBN 1-58488-347-2El postulado de las paralelas es equivalente al postulado de equidistancia , al axioma de Playfair , al axioma de Proclo , al postulado del triángulo y al teorema de Pitágoras .
60. Alexander R. Pruss (2006). El principio de razón suficiente: una reevaluación. Cambridge University Press. pág. 11. ISBN 0-521-85959-XPodríamos incluir... el postulado de las paralelas y derivar el teorema de Pitágoras. O podríamos, en cambio, incluir el teorema de Pitágoras entre los demás axiomas y derivar el postulado de las paralelas .
61. Stephen W. Hawking (2005). Obra citada. Running Press. p. 4. ISBN 0-7624-1922-9.
62. Victor Pambuccian (diciembre de 2010). "Teorema hiperbólico de Pitágoras de María Teresa Calapso". The Mathematical Intelligencer . 32 (4): 2. doi : 10.1007/s00283-010-9169-0 .
63. Barrett O'Neill (2006). "Ejercicio 4". Geometría diferencial elemental (2.ª ed.). Academic Press. pág. 441. ISBN 0-12-088735-5.
64. Saul Stahl (1993). "Teorema 8.3". El semiplano de Poincaré: una puerta de entrada a la geometría moderna . Jones & Bartlett Learning. pág. 122. ISBN 0-86720-298-X.
65. Jane Gilman (1995). "Triángulos hiperbólicos". Subgrupos discretos de dos generadores de PSL(2,R) . Librería de la American Mathematical Society. ISBN 0-8218-0361-1.
66. Tai L. Chow (2000). Métodos matemáticos para físicos: una introducción concisa . Cambridge University Press. pág. 52. ISBN 0-521-65544-7.
67. Neugebauer 1969, pág. 36.
68. Neugebauer 1969: p. 36 "En otras palabras, se sabía durante toda la duración de las matemáticas babilónicas que la suma de los cuadrados de las longitudes de los lados de un triángulo rectángulo es igual al cuadrado de la longitud de la hipotenusa".
69. Friberg, Jöran (1981). "Métodos y tradiciones de las matemáticas babilónicas: Plimpton 322, ternas pitagóricas y ecuaciones paramétricas de triángulos babilónicos". Historia Mathematica . 8 : 277–318. doi : 10.1016/0315-0860(81)90069-0 .:p. 306 "Aunque Plimpton 322 es un texto único en su tipo, hay varios otros textos conocidos que atestiguan que el teorema de Pitágoras era bien conocido por los matemáticos del período babilónico antiguo".
70. Hoyrup, Jens . "'Regla' y 'Teorema' de Pitágoras: espejo de la relación entre las matemáticas babilónicas y griegas". En Renger, Johannes (ed.). Babilonia: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Coloquio Internacional der Deutschen Orient-Gesellschaft 24.–26. Marzo de 1998 en Berlín (PDF) . Berlín: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. págs. 393–407., p. 406, " A juzgar por esta sola evidencia , es probable que la regla pitagórica fuera descubierta dentro del entorno de los agrimensores legos, posiblemente como un derivado del problema tratado en Db ₂ -146, en algún momento entre 2300 y 1825 a. C." ( Db ₂ -146 es una tablilla de arcilla babilónica antigua de Eshnunna relacionada con el cálculo de los lados de un rectángulo dada su área y diagonal).
71. Robson, E. (2008). Matemáticas en el antiguo Irak: una historia social . Princeton University Press.:p. 109 "Muchos matemáticos de la antigua Babilonia… sabían que el cuadrado de la diagonal de un triángulo rectángulo tenía la misma área que la suma de los cuadrados de la longitud y el ancho: esa relación se utiliza en las soluciones resueltas a problemas de palabras sobre 'álgebra' de cortar y pegar en siete tablillas diferentes, de Ešnuna, Sippar, Susa y un lugar desconocido en el sur de Babilonia".
72. Robson, Eleanor (2001). "Ni Sherlock Holmes ni Babilonia: una reevaluación de Plimpton 322". Historia Mathematica . 28 (3): 167–206. doi : 10.1006/hmat.2001.2317 .
73. Kim Plofker (2009). Matemáticas en la India . Princeton University Press. pp. 17-18. ISBN 978-0-691-12067-6.
74. Bartel L. van der Waerden (2012). Geometría y álgebra en las civilizaciones antiguas . Springer Science & Business Media. pág. 26.
75. Carl Benjamin Boyer ; Uta C. Merzbach (2011). "China y la India". Una historia de las matemáticas (3.ª ed.). Wiley. pág. 229. ISBN 978-0470525487Cita: [En los Sulba-sutras,] encontramos reglas para la construcción de ángulos rectos por medio de triples de cuerdas cuyas longitudes forman triajes pitagóricos, como 3, 4 y 5, o 5, 12 y 13, u 8, 15 y 17, o 12, 35 y 37. Aunque la influencia mesopotámica en los Sulvasũtras no es improbable, no conocemos ninguna evidencia concluyente a favor o en contra de esto. Aspastamba sabía que el cuadrado en la diagonal de un rectángulo es igual a la suma de los cuadrados de los dos lados adyacentes. Menos fácil de explicar es otra regla dada por Apastamba, una que se parece mucho a algo del álgebra geométrica del Libro II de los Elementos de Euclides . (...)
76. Proclo (1970). Comentario del primer libro de los Elementos de EuclidesTraducido por Morrow, Glenn R. Princeton University Press. 428.6.
77. "Introducción y libros 1,2". The University Press. 25 de marzo de 1908 – vía Google Books.
78. (Heath 1921, vol. I, p. 144): "Aunque ésta es la proposición que la tradición asocia universalmente con el nombre de Pitágoras, no existe ninguna prueba realmente fiable de que él la haya descubierto. Los autores relativamente tardíos que se la atribuyen añaden la historia de que sacrificó un buey para celebrar su descubrimiento".
79. Se ofrece una amplia discusión de la evidencia histórica en (Euclid 1956, p. 351) página=351
80. Asger Aaboe (1997). Episodios de la historia temprana de las matemáticas. Asociación Matemática de Estados Unidos. p. 51. ISBN 0-88385-613-1... no es hasta Euclides que encontramos una secuencia lógica de teoremas generales con pruebas adecuadas.
81. Robert P. Crease (2008). Las grandes ecuaciones: avances científicos desde Pitágoras hasta Heisenberg. WW Norton & Co. pág. 25. ISBN 978-0-393-06204-5.
82. Christopher Cullen (2007) ofrece un análisis bastante extenso de los orígenes de los diversos textos del Zhou Bi . Astronomía y matemáticas en la antigua China: el "Zhou Bi Suan Jing". Cambridge University Press. págs. 139 y siguientes . ISBN 978-0-521-03537-8.
83. Esta obra es una recopilación de 246 problemas, algunos de los cuales sobrevivieron a la quema de libros del año 213 a. C. y se pusieron en su forma final antes del año 100 d. C. Fue ampliamente comentada por Liu Hui en el año 263 d. C. Philip D. Straffin Jr. (2004). "Liu Hui y la primera edad de oro de las matemáticas chinas". En Marlow Anderson; Victor J. Katz; Robin J. Wilson (eds.). Sherlock Holmes en Babilonia: y otros cuentos de historia matemática . Asociación Matemática de Estados Unidos. pp. 69 y siguientes . ISBN 0-88385-546-1.Véase en particular §3: Nueve capítulos sobre el arte matemático , págs. 71 y siguientes .
84. Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). Los nueve capítulos sobre el arte matemático: guía y comentario. Oxford University Press. pág. 488. ISBN 0-19-853936-3.
85. En particular, Li Jimin; ver Centaurus, volumen 39. Copenhague: Munksgaard. 1997. págs.193, 205.
86. Chen, Cheng-Yih (1996). "§3.3.4 La fórmula de Chén Zǐ y el método Chóng-Chã; Figura 40". Trabajos chinos tempranos en ciencias naturales: una reexaminación de la física del movimiento, la acústica, la astronomía y los pensamientos científicos . Prensa de la Universidad de Hong Kong. pág. 142. ISBN 962-209-385-X.
87. Wen-tsün Wu (2008). "El teorema de Gougu". Obras seleccionadas de Wen-tsün Wu . World Scientific. pág. 158. ISBN 978-981-279-107-8.

Obras citadas

• Bell, John L. (1999). El arte de lo inteligible: un estudio elemental de las matemáticas en su desarrollo conceptual. Kluwer. ISBN 0-7923-5972-0.
• Euclides (1956). Los trece libros de los Elementos de Euclides, traducidos del texto de Heiberg, con introducción y comentario . Vol. 1 (Libros I y II). Traducido por Heath, Thomas L. (Reimpresión de la 2.ª edición (1925)). Dover.Texto en línea en archive.org
• Heath, Sir Thomas (1921). "El 'teorema de Pitágoras'". Una historia de las matemáticas griegas (2 vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. pp. 144 y siguientes . ISBN 0-486-24073-8.
• Libeskind, Shlomo (2008). Geometría euclidiana y transformacional: una investigación deductiva. Jones & Bartlett Learning. ISBN 978-0-7637-4366-6.Este texto de geometría de secundaria cubre muchos de los temas de este artículo de WP.
• Loomis, Elisha Scott (1940). La proposición de Pitágoras (2.ª ed.). Ann Arbor, Michigan: Edwards Brothers. ISBN 9780873530361.Reeditado en 1968 por el Consejo Nacional de Profesores de Matemáticas. El Centro de Información de Recursos Educativos publicó en línea una versión escaneada de menor calidad , ERIC ED037335.
• Maor, Eli (2007). El teorema de Pitágoras: una historia de 4.000 años. Princeton, Nueva Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
• Neugebauer, Otto (1969). Las ciencias exactas en la antigüedad (2.ª ed.). Courier Dover Publications. ISBN 0-486-22332-9.OCLC 638685764  .
• Robson, Eleanor y Jacqueline Stedall, eds., El manual de Oxford de la historia de las matemáticas, Oxford: Oxford University Press, 2009. págs. vii + 918. ISBN 978-0-19-921312-2 . 
• Stillwell, John (1989). Matemáticas y su historia . Springer-Verlag. ISBN 0-387-96981-0.También ISBN 3-540-96981-0 . 
• Swetz, Frank; Kao, TI (1977). ¿ Pitágoras era chino?: Un examen de la teoría del triángulo rectángulo en la antigua China . Prensa de la Universidad Estatal de Pensilvania. ISBN 0-271-01238-2.
• van der Waerden, Bartel Leendert (1983). Geometría y Álgebra en las Civilizaciones Antiguas . Saltador. ISBN 3-540-12159-5. Triples pitagóricos de los escribas babilónicos van der Waerden.

Enlaces externos

• Teorema de Pitágoras en ProofWiki

• Euclides (1997) [c. 300 a. C.]. David E. Joyce (ed.). Elements . Consultado el 30 de agosto de 2006 .En HTML con figuras interactivas basadas en Java.
• "Teorema de Pitágoras". Enciclopedia de Matemáticas . EMS Press . 2001 [1994].
• Tema de historia: El teorema de Pitágoras en las matemáticas babilónicas
• Enlaces interactivos:
  • Demostración interactiva en Java del teorema de Pitágoras
  • Otra demostración interactiva en Java del teorema de Pitágoras
  • Teorema de Pitágoras con animación interactiva
  • Teorema de Pitágoras animado, no algebraico y adaptado al ritmo del usuario
• Demostración del teorema de Pitágoras en el agua en YouTube
• Teorema de Pitágoras (más de 70 demostraciones de corte de nudos )
• Weisstein, Eric W. "Teorema de Pitágoras". MathWorld .