Triángulo de Kepler

Triángulo rectángulo relacionado con la proporción áurea

Un triángulo de Kepler es un triángulo rectángulo formado por tres cuadrados con áreas en progresión geométrica según la proporción áurea .

Un triángulo de Kepler es un triángulo rectángulo especial con longitudes de aristas en progresión geométrica . La razón de la progresión es donde es la proporción áurea , y la progresión se puede escribir: , o aproximadamente . Los cuadrados en las aristas de este triángulo tienen áreas en otra progresión geométrica, . Las definiciones alternativas del mismo triángulo lo caracterizan en términos de las tres medias pitagóricas de dos números, o a través del inradio de los triángulos isósceles . ${\displaystyle {\sqrt {\varphi }}}$ ${\displaystyle \varphi =(1+{\sqrt {5}})/2}$ ${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$ ${\displaystyle 1:1.272:1.618}$ ${\displaystyle 1:\varphi :\varphi ^{2}}$

Este triángulo recibe su nombre de Johannes Kepler , pero se puede encontrar en fuentes anteriores. Aunque algunas fuentes afirman que las pirámides del antiguo Egipto tenían proporciones basadas en un triángulo de Kepler, la mayoría de los estudiosos creen que la proporción áurea no era conocida por los matemáticos y arquitectos egipcios.

Historia

El triángulo de Kepler recibe su nombre del matemático y astrónomo alemán Johannes Kepler (1571-1630), quien escribió sobre esta forma en una carta de 1597. ^[1] Dos conceptos que se pueden utilizar para analizar este triángulo, el teorema de Pitágoras y la proporción áurea, fueron de interés para Kepler, como escribió en otra parte:

La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras, el otro la división de una línea en razones extremas y medias. El primero lo podemos comparar con una masa de oro, el segundo lo podemos llamar una joya preciosa. ^[2]

Sin embargo, Kepler no fue el primero en describir este triángulo. ^[3] El propio Kepler lo atribuyó a "un profesor de música llamado Magirus". ^[1] El mismo triángulo aparece antes en un libro de matemáticas árabes , el Liber mensurationum de Abû Bekr, conocido por una traducción del siglo XII de Gerardo de Cremona al latín, ^{[3] [4]} y en la Practica geometriae  [it] de Fibonacci (publicada en 1220-1221), quien lo definió de manera similar a Kepler. ^{[3] [5]} Un poco antes que Kepler, Pedro Nunes escribió sobre él en 1567, y es "probable que haya estado muy extendido en las tradiciones manuscritas de finales de la Edad Media y del Renacimiento". ^[3] También ha sido redescubierto de forma independiente varias veces, después de Kepler. ^[1]

Triángulo rectángulo formado por el punto medio de una arista, el punto central de la base y el vértice de una pirámide cuadrada . Algunos piramidólogos han teorizado que el triángulo formado de esta manera para la Gran Pirámide de Giza fue concebido como un triángulo de Kepler.

Según algunos autores, una "pirámide áurea" con un triángulo de Kepler doble como su sección transversal describe con precisión el diseño de las pirámides egipcias como la Gran Pirámide de Giza ; una fuente de esta teoría es una lectura errónea de Heródoto del siglo XIX por el piramidólogo John Taylor. ^{[6] [7]} Se han propuesto muchas otras teorías de proporción para la misma pirámide, no relacionadas con el triángulo de Kepler. ^{[1] [6] [8]} Debido a que estas diferentes teorías son muy similares en los valores numéricos que obtienen, y debido a las imprecisiones en la medición, en parte causadas por la destrucción de la superficie exterior de la pirámide, tales teorías son difíciles de resolver basándose puramente en evidencia física. ^{[6] [9]} La coincidencia de proporciones con el triángulo de Kepler bien puede ser una coincidencia numérica: según los académicos que han investigado esta relación, los antiguos egipcios probablemente no conocían ni utilizaban la proporción áurea en sus matemáticas o arquitectura. ^{[1] [8] [10] [11]} En cambio, las proporciones de la pirámide se pueden explicar adecuadamente utilizando razones enteras, basadas en un triángulo rectángulo con lados 11 y 14. ^{[1] [6]}

El nombre "triángulo de Kepler" para esta forma fue utilizado por Roger Herz-Fischler, basándose en la carta de Kepler de 1597, ya en 1979. ^[7] Otro nombre para el mismo triángulo, utilizado por Matila Ghyka en su libro de 1946 sobre la proporción áurea, La geometría del arte y la vida , es el "triángulo de Price", en honor al piramidólogo WA Price. ^[12]

Definiciones

Cuando un triángulo isósceles se forma a partir de dos triángulos de Kepler, reflejados a través de sus lados largos, tiene el radio interno máximo posible entre todos los triángulos isósceles que tienen catetos de un tamaño determinado.

El triángulo de Kepler se define de forma única por las propiedades de ser un triángulo rectángulo y de tener las longitudes de sus lados en progresión geométrica, o equivalentemente tener los cuadrados de sus lados en progresión geométrica. La razón de la progresión de las longitudes de los lados es , donde es la proporción áurea , y la progresión se puede escribir: , o aproximadamente 1 : 1,272 : 1,618. Los cuadrados de los bordes de este triángulo tienen áreas en otra progresión geométrica, . El hecho de que el triángulo con estas proporciones sea un triángulo rectángulo se deduce del hecho de que, para longitudes de aristas cuadradas con estas proporciones, el polinomio definitorio de la proporción áurea es el mismo que la fórmula dada por el teorema de Pitágoras para las longitudes de aristas cuadradas de un triángulo rectángulo: Debido a que esta ecuación es verdadera para la proporción áurea, estas tres longitudes obedecen al teorema de Pitágoras y forman un triángulo rectángulo. Por el contrario, en cualquier triángulo rectángulo cuyas aristas cuadradas estén en progresión geométrica con cualquier razón , el teorema de Pitágoras implica que esta razón obedece a la identidad . Por lo tanto, la razón debe ser la única solución positiva de esta ecuación, la proporción áurea, y el triángulo debe ser un triángulo de Kepler. ^[1] ${\displaystyle {\sqrt {\varphi }}}$ ${\displaystyle \varphi =(1+{\sqrt {5}})/2}$ ${\displaystyle 1:{\sqrt {\varphi }}:\varphi }$ ${\displaystyle 1:\varphi :\varphi ^{2}}$ $${\displaystyle \varphi ^{2}=\varphi +1.}$$ ${\displaystyle \rho }$ ${\displaystyle \rho ^{2}=\rho +1}$

Las tres longitudes de los bordes , y son la media armónica , la media geométrica y la media aritmética , respectivamente, de los dos números . ^{[13] [14]} Estas tres formas de combinar dos números fueron estudiadas en las matemáticas de la antigua Grecia y se denominan medias pitagóricas . ^[15] A la inversa, esto puede tomarse como una definición alternativa del triángulo de Kepler: es un triángulo rectángulo cuyas longitudes de los bordes son las tres medias pitagóricas de algunos dos números. Los únicos triángulos para los que esto es cierto son los triángulos de Kepler. ^{[13] [14]} ${\displaystyle 1}$ ${\displaystyle {\sqrt {\varphi }}}$ ${\displaystyle \varphi }$ ${\displaystyle \varphi \pm 1}$

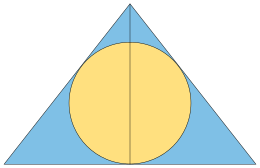
Una tercera forma equivalente de definir este triángulo proviene de un problema de maximización del inradio de los triángulos isósceles . Entre todos los triángulos isósceles con una elección fija de la longitud de los dos lados iguales pero con una longitud de base variable, el que tiene el mayor inradio se forma a partir de dos copias del triángulo de Kepler, reflejadas a través de sus lados más largos entre sí. Por lo tanto, el triángulo de Kepler puede definirse como el triángulo rectángulo que, entre todos los triángulos rectángulos con la misma hipotenusa, forma con su reflexión el triángulo isósceles de máximo inradio. ^[16] La misma reflexión también forma un triángulo isósceles que, para un perímetro dado, contiene el mayor semicírculo posible . ^[17]

Propiedades

En la secuencia loxodrómica de círculos tangentes de Coxeter , los centros de cada tres círculos consecutivos forman un ángulo a partir del triángulo de Kepler.

Si el lado corto de un triángulo de Kepler tiene longitud , los otros lados tendrán longitudes y . El área se puede calcular con la fórmula estándar para el área de triángulos rectángulos (la mitad del producto de los dos lados cortos) como . El coseno del mayor de los dos ángulos no rectos es la razón del lado adyacente (el más corto de los dos lados) a la hipotenusa, , de lo que se deduce que los dos ángulos no rectos son ^[1] ${\displaystyle s}$ ${\displaystyle s{\sqrt {\varphi }}}$ ${\displaystyle s\varphi }$ ${\displaystyle {\tfrac {s^{2}}{2}}{\sqrt {\varphi }}}$ ${\displaystyle \varphi }$

$${\displaystyle \theta =\sin ^{-1}{\frac {1}{\varphi }}\approx 38.1727^{\circ }}$$y $${\displaystyle \theta =\cos ^{-1}{\frac {1}{\varphi }}\approx 51.8273^{\circ }.}$$

Jerzy Kocik ha observado que el mayor de estos dos ángulos es también el ángulo formado por los centros de los triples de círculos consecutivos en la secuencia loxodrómica de círculos tangentes de Coxeter . ^[18]

Véase también

• Triángulo automediano , un triángulo cuyos lados al cuadrado forman una progresión aritmética, incluido el triángulo rectángulo con lados de longitud ${\displaystyle 1:{\sqrt {2}}:{\sqrt {3}}}$
• Triángulo áureo , triángulo isósceles cuya relación entre la base y la longitud del lado es la proporción áurea.

Referencias

1. Herz-Fischler, Roger (2000). La forma de la Gran Pirámide . Waterloo, Ontario: Wilfrid Laurier University Press . ISBN 0-88920-324-5.Señor 1788996  .En todo el libro se examinan muchas teorías alternativas sobre la forma de esta pirámide. Véase el capítulo 11, "Teoría del triángulo de Kepler", págs. 80-91, para material específico sobre el triángulo de Kepler, y la pág. 166 para la conclusión de que la teoría del triángulo de Kepler puede eliminarse mediante el principio de que "Una teoría debe corresponder a un nivel de matemáticas consistente con lo que sabían los antiguos egipcios". Véase la nota 3, pág. 229, para la historia del trabajo de Kepler con este triángulo.
2. Fink, Karl (1903). Breve historia de las matemáticas: traducción autorizada de Geschichte der Elementar-Mathematik, del Dr. Karl Fink. Traducido por Beman, Wooster Woodruff; Smith, David Eugene (2.ª ed.). Chicago: Open Court Publishing Company . pág. 223.
3. Høyrup, Jens (2002). «Reseña de La forma de la Gran Pirámide de Roger Herz-Fischler» (PDF) . Mathematical Reviews . MR  1788996. Archivado (PDF) desde el original el 23 de febrero de 2022. Consultado el 23 de febrero de 2022 .
4. Busard, Hubert LL (abril-junio de 1968). "L'algèbre au Moyen Âge: le" Liber mensurationum "d'Abû Bekr". Journal des Savants (en francés y latín). 1968 (2): 65-124. doi :10.3406/jds.1968.1175. Archivado desde el original el 12 de enero de 2022 . Consultado el 12 de enero de 2022 .Véase el problema 51, reproducido en la pág. 98.
5. Hughes, Barnabas, ed. (2008). Fibonacci's De Practica Geometrie . Fuentes y estudios en la historia de las matemáticas y las ciencias físicas. Nueva York: Springer. pp. 130-131. doi :10.1007/978-0-387-72931-2. ISBN . 978-0-387-72930-5.Señor 2364574  .
6. Bartlett, Christopher (mayo de 2014). "El diseño de la Gran Pirámide de Keops". Nexus Network Journal . 16 (2): 299–311. doi : 10.1007/s00004-014-0193-9 . S2CID  122021107.
7. Fischler, R. (1979). "¿Qué dijo realmente Heródoto? o cómo construir (una teoría de) la Gran Pirámide". Environment and Planning B: Planning and Design . 6 (1): 89–93. Bibcode :1979EnPlB...6...89F. doi :10.1068/b060089. S2CID  62210630.
8. Rossi, Corinna (2004). Arquitectura y matemáticas en el antiguo Egipto . Cambridge University Press. págs. 67-68. ISBN 978-0-521-82954-0... no hay evidencia directa en ninguna fuente matemática escrita del antiguo Egipto de ningún cálculo aritmético o construcción geométrica que pueda clasificarse como la Sección Áurea... la convergencia a , y en sí misma como un número, no encaja con las fuentes matemáticas existentes del Reino Medio ${\displaystyle \varphi }$ ${\displaystyle \varphi }$; véase también un extenso análisis de múltiples teorías alternativas sobre la forma de la pirámide y otras arquitecturas egipcias, págs. 7-56
9. Anglin, WS (1994). "El disparate de la Gran Pirámide". Matemáticas: una historia y filosofía concisas . Textos de pregrado en matemáticas. Nueva York: Springer-Verlag . p. 4. doi :10.1007/978-1-4612-0875-4. ISBN. 0-387-94280-7.Señor 1301327  .
10. Rossi, Corinna ; Tout, Christopher A. (2002). "¿Se conocían la serie de Fibonacci y la sección áurea en el antiguo Egipto?". Historia Mathematica . 29 (2): 101–113. doi : 10.1006/hmat.2001.2334 . hdl : 11311/997099 . MR  1896969.
11. Markowsky, George (enero de 1992). "Misconceptions about the Golden Ratio" (PDF) . The College Mathematics Journal . 23 (1). Mathematical Association of America : 2–19. doi :10.2307/2686193. JSTOR  2686193. Archivado (PDF) desde el original el 2020-12-11 . Consultado el 2012-06-29 . No parece que los egipcios supieran siquiera de la existencia de la proporción áurea y mucho menos que la incorporaran en sus edificios. ${\displaystyle \varphi }$
12. Ghyka, Matila Costiescu (1946). La geometría del arte y la vida. Nueva York: Sheed and Ward . pág. 22.
13. Bruce, Ian (1994). "Otra instancia del triángulo rectángulo áureo" (PDF) . Fibonacci Quarterly . 32 (3): 232–233. doi :10.1080/00150517.1994.12429219. MR  1285752. Archivado (PDF) desde el original el 29 de enero de 2022 . Consultado el 29 de enero de 2022 .
14. Di Domenico, Angelo (julio de 2005). "89.41 La proporción áurea (el triángulo rectángulo) y las medias aritmética, geométrica y armónica". The Mathematical Gazette . 89 (515): 261. doi :10.1017/s0025557200177769. JSTOR  3621234. S2CID  123738769.
15. Huffman, Carl (2005). "Arquitas y la historia de los medios". Arquitas de Tarento: rey pitagórico, filósofo y matemático . Cambridge University Press . págs. 170–177. ISBN. 978-1-139-44407-1Archivado desde el original el 22 de enero de 2022 . Consultado el 22 de enero de 2022 .
16. Halleck, Ezra (marzo de 2012). "Consejo de enseñanza: considere una vaca circular". The College Mathematics Journal . 43 (2): 133. doi :10.4169/college.math.j.43.2.133. JSTOR  10.4169/college.math.j.43.2.133. S2CID  123891402.
17. DeTemple, Duane W. (1992). "El triángulo de perímetro más pequeño que circunscribe un semicírculo" (PDF) . Fibonacci Quarterly . 30 (3): 274. doi :10.1080/00150517.1992.12429354. MR  1175315. Archivado (PDF) desde el original el 2022-01-20 . Consultado el 2022-01-29 .
18. Kocik, Jerzy (enero de 2019). "Una nota sobre empaquetamientos de discos apolíneos no acotados". arXiv : 1910.05924 [math.MG].