
En álgebra abstracta , la teoría de grupos estudia las estructuras algebraicas conocidas como grupos . El concepto de grupo es fundamental para el álgebra abstracta: otras estructuras algebraicas bien conocidas, como anillos , campos y espacios vectoriales , pueden verse como grupos dotados de operaciones y axiomas adicionales . Los grupos se repiten en todas las matemáticas y los métodos de la teoría de grupos han influido en muchas partes del álgebra. Los grupos algebraicos lineales y los grupos de Lie son dos ramas de la teoría de grupos que han experimentado avances y se han convertido en áreas temáticas por derecho propio.
Varios sistemas físicos, como los cristales y el átomo de hidrógeno , y tres de las cuatro fuerzas fundamentales conocidas en el universo, pueden modelarse mediante grupos de simetría . Así, la teoría de grupos y la teoría de la representación, estrechamente relacionada , tienen muchas aplicaciones importantes en física , química y ciencia de materiales . La teoría de grupos también es fundamental para la criptografía de clave pública .
La historia temprana de la teoría de grupos data del siglo XIX. Uno de los logros matemáticos más importantes del siglo XX [1] fue el esfuerzo colaborativo, que ocupó más de 10.000 páginas de revistas y se publicó en su mayoría entre 1960 y 2004, que culminó en una clasificación completa de grupos finitos simples .
La teoría de grupos tiene tres fuentes históricas principales: la teoría de números , la teoría de ecuaciones algebraicas y la geometría . La corriente de la teoría de números fue iniciada por Leonhard Euler y desarrollada por el trabajo de Gauss sobre aritmética modular y grupos aditivos y multiplicativos relacionados con cuerpos cuadráticos . Lagrange , Ruffini y Abel obtuvieron los primeros resultados sobre grupos de permutaciones en su búsqueda de soluciones generales de ecuaciones polinómicas de alto grado. Évariste Galois acuñó el término "grupo" y estableció una conexión, ahora conocida como teoría de Galois , entre la naciente teoría de grupos y la teoría de campos . En geometría, los grupos primero cobraron importancia en la geometría proyectiva y, más tarde, en la geometría no euclidiana . El programa de Erlangen de Felix Klein proclamó que la teoría de grupos era el principio organizador de la geometría.
Galois , en la década de 1830, fue el primero en emplear grupos para determinar la solubilidad de ecuaciones polinómicas . Arthur Cayley y Augustin Louis Cauchy impulsaron estas investigaciones al crear la teoría de los grupos de permutación. La segunda fuente histórica de grupos proviene de situaciones geométricas . En un intento de abordar posibles geometrías (como la geometría euclidiana , hiperbólica o proyectiva ) utilizando la teoría de grupos, Felix Klein inició el programa de Erlangen . Sophus Lie , en 1884, comenzó a utilizar grupos (ahora llamados grupos de Lie ) adjuntos a problemas analíticos . En tercer lugar, los grupos se utilizaron, al principio implícitamente y luego explícitamente, en la teoría algebraica de números .
El diferente alcance de estas primeras fuentes dio como resultado diferentes nociones de grupos. La teoría de grupos se unificó alrededor de 1880. Desde entonces, el impacto de la teoría de grupos ha ido en constante crecimiento, dando lugar al nacimiento del álgebra abstracta a principios del siglo XX, la teoría de la representación y muchos dominios derivados más influyentes. La clasificación de grupos finitos simples es un vasto trabajo de mediados del siglo XX, que clasifica todos los grupos finitos simples .
La gama de grupos considerados se ha ampliado gradualmente desde grupos de permutación finitos y ejemplos especiales de grupos matriciales hasta grupos abstractos que pueden especificarse mediante una presentación por generadores y relaciones .
La primera clase de grupos que se sometió a un estudio sistemático fueron los grupos de permutación . Dado cualquier conjunto X y una colección G de biyecciones de X en sí mismo (conocidas como permutaciones ) que está cerrada bajo composiciones e inversas, G es un grupo que actúa sobre X. Si X consta de n elementos y G consta de todas las permutaciones, G es el grupo simétrico S n ; en general, cualquier grupo de permutación G es un subgrupo del grupo simétrico de X. Una construcción temprana debida a Cayley exhibía cualquier grupo como un grupo de permutación, actuando sobre sí mismo ( X = G ) mediante la representación regular izquierda .
En muchos casos, la estructura de un grupo de permutaciones se puede estudiar utilizando las propiedades de su acción sobre el conjunto correspondiente. De este modo se demuestra, por ejemplo, que para n ≥ 5 el grupo alterno An es simple , es decir, no admite subgrupos normales propios . Este hecho juega un papel clave en la imposibilidad de resolver una ecuación algebraica general de grado n ≥ 5 en radicales .
La siguiente clase importante de grupos está dada por los grupos matriciales o grupos lineales . Aquí G es un conjunto que consta de matrices invertibles de orden dado n sobre un campo K que está cerrado bajo los productos y las inversas. Tal grupo actúa sobre el espacio vectorial n -dimensional K n mediante transformaciones lineales . Esta acción hace que los grupos matriciales sean conceptualmente similares a los grupos de permutación, y la geometría de la acción puede explotarse de manera útil para establecer propiedades del grupo G.
Los grupos de permutación y los grupos de matrices son casos especiales de grupos de transformación : grupos que actúan sobre un determinado espacio X conservando su estructura inherente. En el caso de grupos de permutaciones, X es un conjunto; para grupos de matrices, X es un espacio vectorial . El concepto de grupo de transformación está estrechamente relacionado con el concepto de grupo de simetría : los grupos de transformación frecuentemente consisten en todas las transformaciones que conservan una determinada estructura.
La teoría de los grupos de transformación forma un puente que conecta la teoría de grupos con la geometría diferencial . Una larga línea de investigación, originada con Lie y Klein , considera acciones grupales sobre variedades mediante homeomorfismos o difeomorfismos . Los propios grupos pueden ser discretos o continuos .
La mayoría de los grupos considerados en la primera etapa del desarrollo de la teoría de grupos eran "concretos", ya que se habían realizado mediante números, permutaciones o matrices. No fue hasta finales del siglo XIX que comenzó a afianzarse la idea de un grupo abstracto , donde "abstracto" significa que se ignora la naturaleza de los elementos de tal manera que dos grupos isomórficos son considerados como un mismo grupo. Una forma típica de especificar un grupo abstracto es mediante una presentación por generadores y relaciones ,
Una fuente importante de grupos abstractos viene dada por la construcción de un grupo de factores , o grupo de cocientes , G / H , de un grupo G por un subgrupo normal H. Los grupos de clases de campos numéricos algebraicos estuvieron entre los primeros ejemplos de grupos de factores, de gran interés en la teoría de números . Si un grupo G es un grupo de permutación en un conjunto X , el grupo de factores G / H ya no actúa sobre X ; pero la idea de un grupo abstracto permite no preocuparse por esta discrepancia.
El cambio de perspectiva de los grupos concretos a los abstractos hace que sea natural considerar propiedades de los grupos que son independientes de una realización particular, o en lenguaje moderno, invariantes bajo isomorfismo , así como las clases de grupo con una determinada propiedad de este tipo: grupos finitos , grupos periódicos , grupos simples , grupos solubles , etc. En lugar de explorar las propiedades de un grupo individual, se busca establecer resultados que se apliquen a toda una clase de grupos. El nuevo paradigma fue de suma importancia para el desarrollo de las matemáticas: presagió la creación del álgebra abstracta en las obras de Hilbert , Emil Artin , Emmy Noether y los matemáticos de su escuela. [ cita necesaria ]
Una elaboración importante del concepto de grupo ocurre si G está dotado de una estructura adicional, en particular, de un espacio topológico , variedad diferenciable o variedad algebraica . Si el grupo opera m (multiplicación) e i (inversión),
son compatibles con esta estructura, es decir, son mapas continuos , suaves o regulares (en el sentido de la geometría algebraica), entonces G es un grupo topológico , un grupo de Lie , o un grupo algebraico . [2]
La presencia de estructura extra relaciona este tipo de grupos con otras disciplinas matemáticas y significa que hay más herramientas disponibles en su estudio. Los grupos topológicos forman un dominio natural para el análisis armónico abstracto , mientras que los grupos de Lie (frecuentemente realizados como grupos de transformación) son los pilares de la geometría diferencial y la teoría de la representación unitaria . Ciertas cuestiones de clasificación que no pueden resolverse en general pueden abordarse y resolverse para subclases especiales de grupos. Así, los grupos de Lie compactos y conectados se han clasificado por completo. Existe una relación fructífera entre infinitos grupos abstractos y grupos topológicos: siempre que un grupo Γ puede realizarse como una red en un grupo topológico G , la geometría y el análisis pertenecientes a G arrojan resultados importantes sobre Γ . Una tendencia comparativamente reciente en la teoría de grupos finitos explota sus conexiones con grupos topológicos compactos ( grupos profinitos ): por ejemplo, un solo grupo analítico p -ádico G tiene una familia de cocientes que son p -grupos finitos de varios órdenes y propiedades. de G se traducen en las propiedades de sus cocientes finitos.
Durante el siglo XX, los matemáticos investigaron con gran profundidad algunos aspectos de la teoría de grupos finitos, especialmente la teoría local de grupos finitos y la teoría de grupos solubles y nilpotentes . [ cita necesaria ] Como consecuencia, se logró la clasificación completa de grupos finitos simples , lo que significa que ahora se conocen todos esos grupos simples a partir de los cuales se pueden construir todos los grupos finitos.
Durante la segunda mitad del siglo XX, matemáticos como Chevalley y Steinberg también aumentaron nuestra comprensión de los análogos finitos de los grupos clásicos y otros grupos relacionados. Una de esas familias de grupos es la familia de grupos lineales generales sobre campos finitos . Los grupos finitos suelen aparecer cuando se considera la simetría de objetos matemáticos o físicos, cuando esos objetos admiten sólo un número finito de transformaciones que preservan la estructura. La teoría de los grupos de Lie , que puede considerarse como una " simetría continua ", está fuertemente influenciada por los grupos de Weyl asociados . Se trata de grupos finitos generados por reflexiones que actúan sobre un espacio euclidiano de dimensión finita . Por tanto, las propiedades de los grupos finitos pueden desempeñar un papel en materias como la física teórica y la química .
Decir que un grupo G actúa sobre un conjunto X significa que cada elemento de G define una aplicación biyectiva en el conjunto X de una manera compatible con la estructura del grupo. Cuando X tiene más estructura, es útil restringir aún más esta noción: una representación de G en un espacio vectorial V es un homomorfismo de grupo :
donde GL ( V ) consta de las transformaciones lineales invertibles de V . En otras palabras, a cada elemento del grupo g se le asigna un automorfismo ρ ( g ) tal que ρ ( g ) ∘ ρ ( h ) = ρ ( gh ) para cualquier h en G.
Esta definición puede entenderse en dos direcciones, las cuales dan lugar a dominios completamente nuevos de las matemáticas. [3] Por un lado, puede proporcionar nueva información sobre el grupo G : a menudo, la operación de grupo en G se da de forma abstracta, pero a través de ρ , corresponde a la multiplicación de matrices , lo cual es muy explícito. [4] Por otro lado, dado un grupo bien comprendido que actúa sobre un objeto complicado, esto simplifica el estudio del objeto en cuestión. Por ejemplo, si G es finito, se sabe que V arriba se descompone en partes irreducibles (ver el teorema de Maschke ). Estas partes, a su vez, son mucho más fáciles de manejar que la V completa (a través del lema de Schur ).
Dado un grupo G , la teoría de la representación pregunta qué representaciones de G existen. Hay varios escenarios, y los métodos empleados y los resultados obtenidos son bastante diferentes en cada caso: la teoría de la representación de grupos finitos y las representaciones de grupos de Lie son dos subdominios principales de la teoría. La totalidad de las representaciones está regida por los personajes del grupo . Por ejemplo, los polinomios de Fourier pueden interpretarse como los caracteres de U(1) , el grupo de números complejos de valor absoluto 1 , que actúan sobre el espacio L 2 de funciones periódicas.
Un grupo de Lie es un grupo que también es una variedad diferenciable , con la propiedad de que las operaciones del grupo son compatibles con la estructura suave . Los grupos de Lie llevan el nombre de Sophus Lie , quien sentó las bases de la teoría de los grupos de transformación continua . El término groupes de Lie apareció por primera vez en francés en 1893 en la tesis del alumno de Lie, Arthur Tresse, página 3. [5]
Los grupos de Lie representan la teoría mejor desarrollada de simetría continua de objetos y estructuras matemáticas , lo que los convierte en herramientas indispensables para muchas partes de las matemáticas contemporáneas, así como para la física teórica moderna . Proporcionan un marco natural para analizar las simetrías continuas de ecuaciones diferenciales ( teoría diferencial de Galois ), de la misma manera que los grupos de permutación se utilizan en la teoría de Galois para analizar las simetrías discretas de ecuaciones algebraicas . Una de las principales motivaciones de Lie fue una extensión de la teoría de Galois al caso de grupos de simetría continua.
Los grupos se pueden describir de diferentes maneras. Los grupos finitos se pueden describir escribiendo la tabla de grupos que consta de todas las multiplicaciones posibles g • h . Una forma más compacta de definir un grupo es mediante generadores y relaciones , también llamada presentación de un grupo. Dado cualquier conjunto F de generadores , el grupo libre generado por F se inyecta en el grupo G. El núcleo de este mapa se llama subgrupo de relaciones, generado por algún subconjunto D. La presentación generalmente se denota por. Por ejemplo, la presentación de grupo describe un grupo que es isomorfo a Una cadena que consta de símbolos generadores y sus inversos se llama palabra .
La teoría combinatoria de grupos estudia los grupos desde la perspectiva de los generadores y las relaciones. [6] Es particularmente útil cuando se satisfacen supuestos de finitud, por ejemplo, grupos finitamente generados o grupos finitamente presentados (es decir, además las relaciones son finitas). El área hace uso de la conexión de gráficos a través de sus grupos fundamentales . Por ejemplo, se puede demostrar que cada subgrupo de un grupo libre es libre.
Hay varias preguntas naturales que surgen al dar un grupo por su presentación. El problema verbal pregunta si dos palabras son efectivamente el mismo elemento de grupo. Al relacionar el problema con las máquinas de Turing , se puede demostrar que, en general, no existe ningún algoritmo que resuelva esta tarea. Otro problema algorítmicamente insoluble, generalmente más difícil, es el problema del isomorfismo de grupo , que pregunta si dos grupos dados por presentaciones diferentes son realmente isomorfos. Por ejemplo, el grupo con presentación es isomorfo al grupo aditivo Z de números enteros, aunque esto puede no ser evidente de inmediato. (Escribiendo , uno tiene )

La teoría de grupos geométricos ataca estos problemas desde un punto de vista geométrico, ya sea viendo los grupos como objetos geométricos o encontrando objetos geométricos adecuados sobre los que actúa un grupo. [7] La primera idea se precisa mediante el gráfico de Cayley , cuyos vértices corresponden a elementos del grupo y aristas corresponden a la multiplicación recta en el grupo. Dados dos elementos, se construye la palabra métrica dada por la longitud del camino mínimo entre los elementos. Un teorema de Milnor y Svarc dice entonces que dado un grupo G que actúa de manera razonable en un espacio métrico X , por ejemplo una variedad compacta , entonces G es casi isométrico (es decir, parece similar desde la distancia) al espacio X.
Dado un objeto estructurado X de cualquier tipo, una simetría es un mapeo del objeto sobre sí mismo que preserva la estructura. Esto ocurre en muchos casos, por ejemplo.
Los axiomas de un grupo formalizan los aspectos esenciales de la simetría . Las simetrías forman un grupo: son cerradas porque si tomas la simetría de un objeto y luego aplicas otra simetría, el resultado seguirá siendo una simetría. La identidad que mantiene fijo al objeto es siempre una simetría de un objeto. La existencia de inversas está garantizada deshaciendo la simetría y la asociatividad proviene del hecho de que las simetrías son funciones en un espacio y la composición de funciones es asociativa.
El teorema de Frucht dice que todo grupo es el grupo de simetría de algún grafo . Entonces, cada grupo abstracto es en realidad simetrías de algún objeto explícito.
El dicho de "preservar la estructura" de un objeto se puede precisar trabajando en una categoría . Los mapas que preservan la estructura son entonces los morfismos , y el grupo de simetría es el grupo de automorfismos del objeto en cuestión.
Abundan las aplicaciones de la teoría de grupos. Casi todas las estructuras del álgebra abstracta son casos especiales de grupos. Los anillos , por ejemplo, pueden verse como grupos abelianos (correspondientes a la suma) junto con una segunda operación (correspondiente a la multiplicación). Por lo tanto, los argumentos de la teoría de grupos subyacen a gran parte de la teoría de esas entidades.
La teoría de Galois utiliza grupos para describir las simetrías de las raíces de un polinomio (o más precisamente los automorfismos de las álgebras generadas por estas raíces). El teorema fundamental de la teoría de Galois proporciona un vínculo entre las extensiones de campos algebraicos y la teoría de grupos. Proporciona un criterio eficaz para la solubilidad de ecuaciones polinómicas en términos de la solubilidad del grupo de Galois correspondiente . Por ejemplo, S 5 , el grupo simétrico de 5 elementos, no tiene solución, lo que implica que la ecuación quíntica general no puede resolverse mediante radicales como lo hacen las ecuaciones de grado inferior. La teoría, al ser una de las raíces históricas de la teoría de grupos, todavía se aplica fructíferamente para producir nuevos resultados en áreas como la teoría de campos de clases .
La topología algebraica es otro dominio que asocia de manera destacada grupos con los objetos que interesan a la teoría. Allí, los grupos se utilizan para describir ciertas invariantes de espacios topológicos . Se denominan "invariantes" porque se definen de tal manera que no cambian si el espacio se somete a alguna deformación . Por ejemplo, el grupo fundamental "cuenta" cuántos caminos en el espacio son esencialmente diferentes. La conjetura de Poincaré , demostrada en 2002/2003 por Grigori Perelman , es una aplicación destacada de esta idea. Sin embargo, la influencia no es unidireccional. Por ejemplo, la topología algebraica utiliza espacios de Eilenberg-MacLane , que son espacios con grupos de homotopía prescritos . De manera similar, la teoría K algebraica se basa en cierto modo en la clasificación de espacios de grupos. Finalmente, el nombre del subgrupo de torsión de un grupo infinito muestra el legado de la topología en la teoría de grupos.

La geometría algebraica también utiliza la teoría de grupos de muchas maneras. Las variedades abelianas se han introducido anteriormente. La presencia de la operación en grupo aporta información adicional que hace que estas variedades sean especialmente accesibles. También suelen servir como prueba para nuevas conjeturas. (Por ejemplo, la conjetura de Hodge (en ciertos casos).) Se estudia con especial detalle el caso unidimensional, es decir, las curvas elípticas . Son tanto teórica como prácticamente intrigantes. [8] En otra dirección, las variedades tóricas son variedades algebraicas sobre las que actúa un toro . Las incrustaciones toroidales han conducido recientemente a avances en geometría algebraica , en particular en la resolución de singularidades . [9]
La teoría algebraica de números utiliza grupos para algunas aplicaciones importantes. Por ejemplo, la fórmula del producto de Euler ,
Capta el hecho de que cualquier número entero se descompone de forma única en números primos . El fracaso de esta afirmación para anillos más generales da lugar a grupos de clases y primos regulares , que aparecen en el tratamiento que hace Kummer del último teorema de Fermat .
El análisis de grupos de Lie y algunos otros grupos se denomina análisis armónico . Las medidas de Haar , es decir, integrales invariantes bajo la traducción en un grupo de Lie, se utilizan para el reconocimiento de patrones y otras técnicas de procesamiento de imágenes . [10]
En combinatoria , la noción de grupo de permutación y el concepto de acción grupal se suelen utilizar para simplificar el recuento de un conjunto de objetos; ver en particular el lema de Burnside .
La presencia de la periodicidad 12 en el círculo de quintas produce aplicaciones de la teoría elemental de grupos en la teoría de conjuntos musicales . La teoría transformacional modela las transformaciones musicales como elementos de un grupo matemático.
En física , los grupos son importantes porque describen las simetrías que parecen obedecer las leyes de la física. Según el teorema de Noether , toda simetría continua de un sistema físico corresponde a una ley de conservación del sistema. Los físicos están muy interesados en las representaciones de grupos, especialmente de los grupos de Lie, ya que estas representaciones a menudo señalan el camino hacia las "posibles" teorías físicas. Ejemplos del uso de grupos en física incluyen el modelo estándar , la teoría de calibre , el grupo de Lorentz y el grupo de Poincaré .
La teoría de grupos se puede utilizar para resolver la incompletitud de las interpretaciones estadísticas de la mecánica desarrolladas por Willard Gibbs , relacionadas con la suma de un número infinito de probabilidades para producir una solución significativa. [11]
En química y ciencia de materiales , los grupos de puntos se utilizan para clasificar los poliedros regulares y las simetrías de las moléculas , y los grupos espaciales para clasificar las estructuras cristalinas . Los grupos asignados se pueden usar para determinar propiedades físicas (como polaridad química y quiralidad ), propiedades espectroscópicas (particularmente útiles para espectroscopia Raman , espectroscopia infrarroja , espectroscopia de dicroísmo circular, espectroscopia de dicroísmo circular magnético, espectroscopia UV/Vis y espectroscopia de fluorescencia). y construir orbitales moleculares .
La simetría molecular es responsable de muchas propiedades físicas y espectroscópicas de los compuestos y proporciona información relevante sobre cómo ocurren las reacciones químicas. Para asignar un grupo de puntos a cualquier molécula dada, es necesario encontrar el conjunto de operaciones de simetría presentes en ella. La operación de simetría es una acción, como una rotación alrededor de un eje o una reflexión a través de un plano especular. En otras palabras, es una operación que mueve la molécula de tal manera que es indistinguible de la configuración original. En teoría de grupos, los ejes de rotación y los planos especulares se denominan "elementos de simetría". Estos elementos pueden ser un punto, recta o plano respecto del cual se realiza la operación de simetría. Las operaciones de simetría de una molécula determinan el grupo de puntos específico de esta molécula.

En química , existen cinco operaciones de simetría importantes. Son operación de identidad ( E) , operación de rotación o rotación propia ( C n ), operación de reflexión ( σ ), operación de inversión ( i ) y operación de rotación reflexión o rotación impropia ( S n ). La operación de identidad ( E ) consiste en dejar la molécula como está. Esto equivale a cualquier número de rotaciones completas alrededor de cualquier eje. Ésta es una simetría de todas las moléculas, mientras que el grupo de simetría de una molécula quiral consta únicamente de la operación de identidad. Una operación de identidad es una característica de toda molécula incluso si no tiene simetría. La rotación alrededor de un eje ( C n ) consiste en girar la molécula alrededor de un eje específico en un ángulo específico. Es una rotación a través del ángulo 360°/ n , donde n es un número entero, alrededor de un eje de rotación. Por ejemplo, si una molécula de agua gira 180° alrededor del eje que pasa por el átomo de oxígeno y entre los átomos de hidrógeno , está en la misma configuración que al principio. En este caso, n = 2 , ya que al aplicarlo dos veces se produce la operación identidad. En moléculas con más de un eje de rotación, el eje C n que tiene el valor más grande de n es el eje de rotación de mayor orden o eje principal. Por ejemplo, en el trifluoruro de boro (BF 3 ), el eje de rotación de mayor orden es C 3 , por lo que el eje de rotación principal es C 3 .
En la operación de reflexión ( σ ) muchas moléculas tienen planos especulares, aunque pueden no ser obvios. La operación de reflexión intercambia izquierda y derecha, como si cada punto se hubiera movido perpendicularmente a través del plano hasta una posición exactamente tan alejada del plano como cuando comenzó. Cuando el plano es perpendicular al eje principal de rotación, se denomina σ h (horizontal). Otros planos, que contienen el eje principal de rotación, están etiquetados como verticales ( σ v ) o diédricos ( σ d ).
La inversión (i) es una operación más compleja. Cada punto se mueve a través del centro de la molécula hasta una posición opuesta a la posición original y tan lejos del punto central como donde comenzó. Muchas moléculas que a primera vista parecen tener un centro de inversión no lo tienen; por ejemplo, el metano y otras moléculas tetraédricas carecen de simetría de inversión. Para ver esto, sostenga un modelo de metano con dos átomos de hidrógeno en el plano vertical de la derecha y dos átomos de hidrógeno en el plano horizontal de la izquierda. La inversión da como resultado dos átomos de hidrógeno en el plano horizontal de la derecha y dos átomos de hidrógeno en el plano vertical de la izquierda. Por lo tanto, la inversión no es una operación de simetría del metano, porque la orientación de la molécula después de la operación de inversión difiere de la orientación original. Y la última operación es rotación impropia o operación de reflexión de rotación ( S n ) requiere una rotación de 360°/ n , seguida de una reflexión a través de un plano perpendicular al eje de rotación.
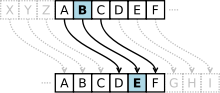
Para la criptografía de clave pública sirven grupos muy grandes de orden primo construidos en criptografía de curva elíptica . Los métodos criptográficos de este tipo se benefician de la flexibilidad de los objetos geométricos, de ahí sus estructuras de grupo, junto con la complicada estructura de estos grupos, que hacen que el logaritmo discreto sea muy difícil de calcular. Uno de los primeros protocolos de cifrado, el cifrado de César , también puede interpretarse como una operación grupal (muy sencilla). La mayoría de los esquemas criptográficos utilizan grupos de alguna manera. En particular, el intercambio de claves Diffie-Hellman utiliza grupos cíclicos finitos . Entonces, el término criptografía basada en grupos se refiere principalmente a protocolos criptográficos que utilizan infinitos grupos no abelianos , como un grupo trenzado .