Geodésicas sobre un elipsoide

Caminos más cortos en una superficie cuádrica delimitada y deformada en forma de esfera

Una geodésica sobre un elipsoide achatado.

El estudio de las geodésicas sobre un elipsoide surgió en relación con la geodesia específicamente con la solución de redes de triangulación . La figura de la Tierra está bien aproximada mediante un elipsoide achatado , una esfera ligeramente aplanada. Una geodésica es el camino más corto entre dos puntos en una superficie curva, análoga a una línea recta en una superficie plana. La solución de una red de triangulación sobre un elipsoide es, por tanto, un conjunto de ejercicios de trigonometría esferoidal (Euler 1755).

Si se trata la Tierra como una esfera , las geodésicas son círculos máximos (todos cerrados) y los problemas se reducen a los de trigonometría esférica . Sin embargo, Newton (1687) demostró que el efecto de la rotación de la Tierra hace que ésta se parezca a un elipsoide ligeramente achatado: en este caso, el ecuador y los meridianos son las únicas geodésicas cerradas simples. Además, el camino más corto entre dos puntos del ecuador no necesariamente discurre a lo largo del ecuador. Finalmente, si el elipsoide se perturba aún más para convertirse en un elipsoide triaxial (con tres semiejes distintos), sólo se cierran tres geodésicas.

Geodésicas sobre un elipsoide de revolución.

Hay varias formas de definir las geodésicas (Hilbert y Cohn-Vossen 1952, págs. 220-221). Una definición simple es como el camino más corto entre dos puntos de una superficie. Sin embargo, frecuentemente es más útil definirlos como caminos con curvatura geodésica cero , es decir, el análogo de líneas rectas sobre una superficie curva. Esta definición abarca geodésicas que viajan tan lejos a través de la superficie del elipsoide que comienzan a regresar hacia el punto de partida, de modo que otras rutas son más directas, e incluye caminos que se cruzan o vuelven a trazarse. Los segmentos suficientemente cortos de una geodésica siguen siendo la ruta más corta entre sus puntos finales, pero las geodésicas no son necesariamente globalmente mínimas (es decir, la más corta entre todas las rutas posibles). Todo camino globalmente más corto es una geodésica, pero no al revés.

A finales del siglo XVIII, un elipsoide de revolución (también se utiliza el término esferoide ) era una aproximación bien aceptada a la figura de la Tierra . El ajuste de las redes de triangulación implicó reducir todas las medidas a un elipsoide de referencia y resolver el problema bidimensional resultante como un ejercicio de trigonometría esferoidal (Bomford 1952, Cap. 3) (Leick et al. 2015, §4.5).

Fig. 1. Un AB geodésico sobre un elipsoide de revolución. N es el polo norte y EFH se encuentra en el ecuador.

Es posible reducir los diversos problemas geodésicos a uno de dos tipos. Considere dos puntos: A en latitud φ ₁ y longitud λ ₁ y B en latitud φ ₂ y longitud λ ₂ (ver Fig. 1). La geodésica de conexión (de A a B ) es AB , de longitud s ₁₂ , que tiene acimutes α ₁ y α ₂ en los dos puntos extremos. ^[1] Los dos problemas geodésicos generalmente considerados son:

1. el problema geodésico directo o primer problema geodésico , dados A , α ₁ y s ₁₂ , determine B y α ₂ ;
2. el problema geodésico inverso o segundo problema geodésico , dados A y B , determina s ₁₂ , α ₁ y α ₂ .

Como puede verse en la Fig. 1, estos problemas implican resolver el triángulo NAB dado un ángulo, α ₁ para el problema directo y λ ₁₂ = λ ₂ − λ ₁ para el problema inverso, y sus dos lados adyacentes. Para una esfera las soluciones a estos problemas son ejercicios simples de trigonometría esférica , cuya solución viene dada por fórmulas para resolver un triángulo esférico . (Consulte el artículo sobre navegación en círculo máximo ).

Para un elipsoide de revolución, Clairaut (1735) encontró la constante característica que define la geodésica. Legendre (1806) y Oriani (1806) (y artículos posteriores de 1808 y 1810) dieron una solución sistemática para los caminos de las geodésicas. Bessel (1825) da la solución completa para el problema directo (completa con tablas computacionales y un ejemplo resuelto).

Durante el siglo XVIII, las geodésicas se denominaban "líneas más cortas". El término "línea geodésica" (en realidad, una curva ) fue acuñado por Laplace (1799b):

Nous désignerons cette ligne sous le nom de ligne géodésique [Llamaremos a esta línea línea geodésica ].

Esta terminología se introdujo en inglés como "línea geodésica" o como "línea geodésica", por ejemplo (Hutton 1811, p. 115),

Una línea trazada en la forma que acabamos de describir, o deducida de medidas trigonométricas, por los medios que hemos indicado, se llama línea geodésica o geodésica: tiene la propiedad de ser la más corta que se puede trazar entre sus dos extremos en la superficie de la Tierra; y es por tanto la medida de itinerario adecuada de la distancia entre esos dos puntos.

En su adopción por otros campos , se prefirió la línea geodésica , frecuentemente abreviada como geodésica .

Esta sección trata el problema de un elipsoide de revolución (tanto achatado como alargado). El problema de un elipsoide triaxial se trata en la siguiente sección.

Ecuaciones para una geodésica

Aquí se desarrollan las ecuaciones para una geodésica; la derivación sigue de cerca la de Bessel (1825). Jordan & Eggert (1941), Bagratuni (1962, §15), Gan'shin (1967, Cap. 5), Krakiwsky & Thomson (1974, §4), Rapp (1993, §1.2), Jekeli (2012) y Borre y Strang (2012) también proporcionan derivaciones de estas ecuaciones.

Considere un elipsoide de revolución con radio ecuatorial a y semieje polar b . Defina el aplanamiento f , la excentricidad e y la segunda excentricidad e ′ :

${\displaystyle f={\frac {a-b}{a}},\quad e={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\sqrt {f(2-f)}},\quad e'={\frac {\sqrt {a^{2}-b^{2}}}{b}}={\frac {e}{1-f}}.}$

(En la mayoría de las aplicaciones en geodesia, el elipsoide se considera achatado, a > b ; sin embargo, la teoría se aplica sin cambios a elipsoides alargados, a < b , en cuyo caso f , e ² y e ′ ² son negativos.)

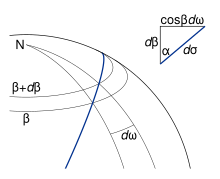
Sea un segmento elemental de una trayectoria en el elipsoide que tenga longitud ds . De las Figs. 2 y 3, vemos que si su acimut es α , entonces ds está relacionado con dφ y dλ por

${\displaystyle \cos \alpha \,ds=\rho \,d\varphi =-{\frac {dR}{\sin \varphi }},\quad \sin \alpha \,ds=R\,d\lambda ,}$ (1)

donde ρ es el radio de curvatura meridional , R = ν cos φ es el radio del círculo de latitud φ , y ν es el radio de curvatura normal . Por tanto, el segmento elemental viene dado por

${\displaystyle ds^{2}=\rho ^{2}\,d\varphi ^{2}+R^{2}\,d\lambda ^{2}}$

o

${\displaystyle {\begin{aligned}ds&={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\&\equiv L(\varphi ,\varphi ')\,d\lambda ,\end{aligned}}}$

donde φ ′ = dφ / dλ y la función lagrangiana L depende de φ a través de ρ( φ ) y R ( φ ) . La longitud de un camino arbitrario entre ( φ ₁ , λ ₁ ) y ( φ ₂ , λ ₂ ) viene dada por

${\displaystyle s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi ,\varphi ')\,d\lambda ,}$

donde φ es una función de λ que satisface φ ( λ ₁ ) = φ ₁ y φ ( λ ₂ ) = φ ₂ . El camino más corto o geodésico implica encontrar aquella función φ ( λ ) que minimice s ₁₂ . Este es un ejercicio de cálculo de variaciones y la condición minimizadora está dada por la identidad de Beltrami ,

${\displaystyle L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}}$

Sustituyendo L y usando las Ecs. (1) da

${\displaystyle R\sin \alpha ={\text{const.}}}$

Clairaut (1735) encontró esta relación , utilizando una construcción geométrica; Lyusternik (1964, §10) presenta una derivación similar. ^[2] Diferenciar esta relación da

${\displaystyle d\alpha =\sin \varphi \,d\lambda .}$

Esto, junto con las Ecs. (1) , conduce a un sistema de ecuaciones diferenciales ordinarias para una geodésica

${\displaystyle {\frac {d\varphi }{ds}}={\frac {\cos \alpha }{\rho }};\quad {\frac {d\lambda }{ds}}={\frac {\sin \alpha }{\nu \cos \varphi }};\quad {\frac {d\alpha }{ds}}={\frac {\tan \varphi \sin \alpha }{\nu }}.}$

Podemos expresar R en términos de la latitud paramétrica , β , usando

${\displaystyle R=a\cos \beta ,}$

y la relación de Claraut entonces se vuelve

${\displaystyle \sin \alpha _{1}\cos \beta _{1}=\sin \alpha _{2}\cos \beta _{2}.}$

Esta es la regla del seno de la trigonometría esférica que relaciona dos lados del triángulo NAB (ver Fig. 4), NA = 1 ⁄ 2 π − β ₁ y NB = 1 ⁄ 2 π − β ₂ y sus ángulos opuestos B = π − α ₂ y A = α ₁ .

Para encontrar la relación para el tercer lado AB = σ ₁₂ , la longitud del arco esférico , y el ángulo incluido N = ω ₁₂ , la longitud esférica , es útil considerar el triángulo NEP que representa una geodésica que comienza en el ecuador; ver Fig. 5. En esta figura, las variables referidas a la esfera auxiliar se muestran con las cantidades correspondientes al elipsoide que se muestran entre paréntesis. Las cantidades sin subíndices se refieren al punto arbitrario P ; E , el punto en el que la geodésica cruza el ecuador en dirección norte, se utiliza como origen para σ , s y ω .

Fig. 6. Elemento diferencial de una geodésica sobre una esfera.

Si el lado EP se extiende moviendo P infinitamente (ver Fig. 6), obtenemos

${\displaystyle \cos \alpha \,d\sigma =d\beta ,\quad \sin \alpha \,d\sigma =\cos \beta \,d\omega .}$ (2)

Combinando las ecuaciones. (1) y (2) dan ecuaciones diferenciales para s y λ

${\displaystyle {\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\frac {\sin \beta }{\sin \varphi }}.}$

La relación entre β y φ es

${\displaystyle \tan \beta ={\sqrt {1-e^{2}}}\tan \varphi =(1-f)\tan \varphi ,}$

lo que da

${\displaystyle {\frac {\sin \beta }{\sin \varphi }}={\sqrt {1-e^{2}\cos ^{2}\beta }},}$

de modo que las ecuaciones diferenciales para la geodésica se convierten en

${\displaystyle {\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\sqrt {1-e^{2}\cos ^{2}\beta }}.}$

El último paso es utilizar σ como parámetro independiente en ambas ecuaciones diferenciales y así expresar s y λ como integrales. Aplicando la regla del seno a los vértices E y G en el triángulo esférico EGP en la Fig. 5 se obtiene

${\displaystyle \sin \beta =\sin \beta (\sigma ;\alpha _{0})=\cos \alpha _{0}\sin \sigma ,}$

donde α ₀ es el azimut en E . Sustituyendo esto en la ecuación para ds / d σ e integrando el resultado se obtiene

${\displaystyle {\frac {s}{b}}=\int _{0}^{\sigma }{\sqrt {1+k^{2}\sin ^{2}\sigma '}}\,d\sigma ',}$ (3)

dónde

${\displaystyle k=e'\cos \alpha _{0},}$

y los límites de la integral se eligen de modo que s ( σ = 0) = 0 . Legendre (1811, p. 180) señaló que la ecuación para s es la misma que la ecuación para el arco en una elipse con semiejes b √ 1 + e ′ ² cos ² α ₀ y b . Para expresar la ecuación de λ en términos de σ , escribimos

${\displaystyle d\omega ={\frac {\sin \alpha _{0}}{\cos ^{2}\beta }}\,d\sigma ,}$

que se sigue de la ecuación. 2 y la relación de Clairaut. Esto produce

${\displaystyle \lambda -\lambda _{0}=\omega -f\sin \alpha _{0}\int _{0}^{\sigma }{\frac {2-f}{1+(1-f){\sqrt {1+k^{2}\sin ^{2}\sigma '}}}}\,d\sigma ',}$ (4)

y los límites de las integrales se eligen de modo que λ = λ ₀ en el cruce del ecuador, σ = 0 .

Esto completa la solución del camino de una geodésica utilizando la esfera auxiliar. Con este dispositivo se puede trazar un círculo máximo exactamente en una geodésica sobre un elipsoide de revolución.

También hay varias formas de aproximar geodésicas en un elipsoide terrestre (con un pequeño aplanamiento) (Rapp 1991, §6); algunos de ellos se describen en el artículo sobre distancia geográfica . Sin embargo, estos suelen ser comparables en complejidad al método para la solución exacta (Jekeli 2012, §2.1.4).

Comportamiento de las geodésicas

Fig. 7. Los meridianos y el ecuador son las únicas geodésicas cerradas. (Para los elipsoides muy aplanados, existen otras geodésicas cerradas; ver Figs. 11 y 12).

Geodésica sobre un elipsoide achatado ( f = 1 ⁄ 50 ) con α ₀ =45° .

Fig. 10. Geodésica sobre un elipsoide alargado ( f = − 1 ⁄ 50 ) con α ₀ =45° . Comparar con la Fig. 8.

La Fig. 7 muestra las geodésicas cerradas simples que constan de los meridianos (verde) y el ecuador (rojo). (Aquí la calificación "simple" significa que la geodésica se cierra sobre sí misma sin una autointersección intermedia). Esto se desprende de las ecuaciones para las geodésicas dadas en la sección anterior.

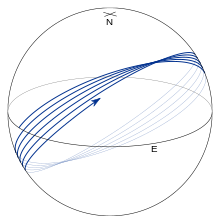
Todas las demás geodésicas están tipificadas en las Figs. 8 y 9 que muestran una geodésica que comienza en el ecuador con α ₀ = 45° . La geodésica oscila alrededor del ecuador. Los cruces ecuatoriales se denominan nodos y los puntos de máxima o mínima latitud se denominan vértices ; las latitudes paramétricas de los vértices están dadas por β = ±( 1 ⁄ 2 π − |α ₀ |) . La geodésica completa una oscilación completa en latitud antes de que la longitud haya aumentado en360° . Por lo tanto, en cada cruce sucesivo del ecuador hacia el norte (ver Fig. 8), λ se queda corto de un circuito completo del ecuador en aproximadamente 2 π f senα ₀ (para un elipsoide alargado, esta cantidad es negativa y λ completa más que un circuito completo, ver Fig. 10). Para casi todos los valores de α ₀ , la geodésica llenará esa porción del elipsoide entre las dos latitudes del vértice (ver Fig. 9).

Dos geodésicas cerradas adicionales para el elipsoide achatado, b ⁄ a = 2 ⁄ 7 .

Si el elipsoide es suficientemente achatado, es decir, b ⁄ a < 1 ⁄ 2 , es posible otra clase de geodésicas cerradas simples (Klingenberg 1982, §3.5.19). Dos de estas geodésicas se ilustran en las Figs. 11 y 12. Aquí b ⁄ a = 2 ⁄ 7 y se elige el acimut ecuatorial, α _{0 , para la geodésica verde (resp. azul)}53,175° (resp.75,192° ), de modo que la geodésica completa 2 (o 3) oscilaciones completas alrededor del ecuador en un circuito del elipsoide.

Fig. 13. Geodésicas (azul) desde un solo punto para f = 1 ⁄ 10 , φ ₁ =−30° ; Los círculos geodésicos se muestran en verde y el lugar de corte en rojo.

La Fig. 13 muestra geodésicas (en azul) que emanan de A con α ₁ un múltiplo de15° hasta el punto en que dejen de ser caminos más cortos. (El aplanamiento se ha aumentado a 1 ⁄ 10 para acentuar los efectos elipsoidales). También se muestran (en verde) curvas de constante s 12 _, que son los círculos geodésicos centrados en A. Gauss (1828) demostró que, en cualquier superficie, las geodésicas y el círculo geodésico se cruzan en ángulos rectos. La línea roja es el lugar de corte , el lugar de los puntos que tienen múltiples (dos en este caso) geodésicas más cortas de A. En una esfera, el lugar de corte es un punto. En un elipsoide achatado (que se muestra aquí), es un segmento del círculo de latitud centrado en el punto antípoda de A , φ = − φ ₁ . La extensión longitudinal del lugar de corte es aproximadamente λ ₁₂ ∈ [ π − f π cos φ ₁ , π + f π cos φ ₁ ] . Si A se encuentra en el ecuador, φ ₁ = 0 , esta relación es exacta y, como consecuencia, el ecuador es sólo una geodésica más corta si | λ12 |_​ ≤ (1 − f ) π . Para un elipsoide alargado, el lugar de corte es un segmento del antimeridiano centrado en el punto antípoda de A , λ ₁₂ = π , y esto significa que las geodésicas meridionales dejan de ser caminos más cortos antes de alcanzar la antípoda.

Propiedades diferenciales de las geodésicas.

Varios problemas relacionados con las geodésicas requieren conocer su comportamiento cuando son perturbadas. Esto es útil en ajustes trigonométricos (Ehlert 1993), determinando las propiedades físicas de las señales que siguen a las geodésicas, etc. Considere una geodésica de referencia, parametrizada por s , y una segunda geodésica a una pequeña distancia t ( s ) de ella. Gauss (1828) demostró que t ( s ) obedece a la ecuación de Gauss-Jacobi

${\displaystyle {\frac {d^{2}t(s)}{ds^{2}}}+K(s)t(s)=0,}$

Fig. 14. Definición de longitud reducida y escala geodésica.

donde K ( s ) es la curvatura gaussiana en s . Como ecuación diferencial lineal, homogénea y de segundo orden, su solución puede expresarse como la suma de dos soluciones independientes.

${\displaystyle t(s_{2})=Cm(s_{1},s_{2})+DM(s_{1},s_{2})}$

dónde

${\displaystyle {\begin{aligned}m(s_{1},s_{1})&=0,\quad \left.{\frac {dm(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=1,\\M(s_{1},s_{1})&=1,\quad \left.{\frac {dM(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=0.\end{aligned}}}$

La cantidad m ( s ₁ , s ₂ ) = m ₁₂ es la llamada longitud reducida , y M ( s ₁ , s ₂ ) = M ₁₂ es la escala geodésica . ^[3] Sus definiciones básicas se ilustran en la Fig. 14.

La curvatura gaussiana para un elipsoide de revolución es

${\displaystyle K={\frac {1}{\rho \nu }}={\frac {{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}{b^{2}}}={\frac {b^{2}}{a^{4}{\bigl (}1-e^{2}\cos ^{2}\beta {\bigr )}^{2}}}.}$

Helmert (1880, Ec. (6.5.1.)) resolvió la ecuación de Gauss-Jacobi para este caso permitiendo expresar m ₁₂ y M _{12 como integrales.}

Como vemos en la Fig. 14 (subfigura superior), la separación de dos geodésicas que comienzan en el mismo punto con acimutes que difieren en d α ₁ es m ₁₂ d α ₁ . En una superficie cerrada como un elipsoide, m ₁₂ oscila alrededor de cero. El punto en el que m ₁₂ se vuelve cero es el punto conjugado con el punto inicial. Para que una geodésica entre A y B , de longitud s ₁₂ , sea el camino más corto debe satisfacer la condición de Jacobi (Jacobi 1837) (Jacobi 1866, §6) (Forsyth 1927, §§26-27) (Bliss 1916 ), que no existe ningún punto conjugado a A entre A y B . Si esta condición no se cumple, entonces hay un camino cercano (no necesariamente geodésico) que es más corto. Por tanto, la condición de Jacobi es una propiedad local de la geodésica y es sólo una condición necesaria para que la geodésica sea el camino más corto global. Condiciones necesarias y suficientes para que una geodésica sea el camino más corto son:

• para un elipsoide achatado, | σ12 |_​ ≤π ;​
• para un elipsoide alargado, | λ12 |_​ ≤ π , si α ₀ ≠ 0 ; si α ₀ = 0 , se requiere la condición suplementaria m ₁₂ ≥ 0 si | λ12 |_​ = π .

Envoltura de geodésicas

Geodésicas desde un solo punto ( f = 1 ⁄ 10 , φ ₁ =−30° )

Las geodésicas desde un punto particular A , si continúan más allá del lugar de corte, forman una envoltura ilustrada en la Fig. 15. Aquí las geodésicas para las cuales α ₁ es un múltiplo de3° se muestran en azul claro. (Las geodésicas sólo se muestran en su primer paso cerca de la antípoda, no en los siguientes). Algunos círculos geodésicos se muestran en verde; estos forman cúspides en el sobre. El lugar del corte se muestra en rojo. La envolvente es el lugar geométrico de los puntos conjugados con A ; Los puntos de la envolvente se pueden calcular encontrando el punto en el que m ₁₂ = 0 en una geodésica. Jacobi (1891) llama astroide a esta figura parecida a una estrella producida por la envoltura .

Fuera del astroide, dos geodésicas se cruzan en cada punto; por tanto, hay dos geodésicas (con una longitud de aproximadamente la mitad de la circunferencia del elipsoide) entre A y estos puntos. Esto corresponde a la situación en la esfera donde hay rutas "cortas" y "largas" en un círculo máximo entre dos puntos. Dentro del astroide, cuatro geodésicas se cruzan en cada punto. Cuatro de estas geodésicas se muestran en la Fig. 16, donde las geodésicas están numeradas en orden creciente de longitud. (Esta figura usa la misma posición para A que la Fig. 13 y está dibujada en la misma proyección). Las dos geodésicas más cortas son estables , es decir, m ₁₂ > 0 , de modo que no hay un camino cercano que conecte los dos puntos que sea más corto. ; los otros dos son inestables. Sólo la recta más corta (la primera) tiene σ ₁₂ ≤ π . Todas las geodésicas son tangentes a la envolvente que se muestra en verde en la figura.

El astroide es la evolución ( exterior) de los círculos geodésicos centrados en A. Asimismo, los círculos geodésicos son involutas del astroide.

Área de un polígono geodésico

Un polígono geodésico es un polígono cuyos lados son geodésicos. Es análogo a un polígono esférico , cuyos lados son círculos máximos. El área de dicho polígono se puede encontrar calculando primero el área entre un segmento geodésico y el ecuador, es decir, el área del cuadrilátero AFHB en la Fig. 1 (Danielsen 1989). Una vez conocida esta área, el área de un polígono se puede calcular sumando las contribuciones de todos los bordes del polígono.

Aquí se desarrolla una expresión para el área S ₁₂ de AFHB siguiendo a Sjöberg (2006). El área de cualquier región cerrada del elipsoide es

${\displaystyle T=\int dT=\int {\frac {1}{K}}\cos \varphi \,d\varphi \,d\lambda ,}$

donde dT es un elemento de área superficial y K es la curvatura gaussiana . Ahora el teorema de Gauss-Bonnet aplicado a los estados de un polígono geodésico

${\displaystyle \Gamma =\int K\,dT=\int \cos \varphi \,d\varphi \,d\lambda ,}$

dónde

${\displaystyle \Gamma =2\pi -\sum _{j}\theta _{j}}$

es el exceso geodésico y θ _j es el ángulo exterior en el vértice j . Multiplicando la ecuación para Γ por R ₂ ² , donde R ₂ es el radio autálico , y restando esto de la ecuación para T se obtiene

${\displaystyle {\begin{aligned}T&=R_{2}^{2}\,\Gamma +\int \left({\frac {1}{K}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda \\&=R_{2}^{2}\,\Gamma +\int \left({\frac {b^{2}}{{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda ,\end{aligned}}}$

donde se ha sustituido el valor de K por un elipsoide . Aplicando esta fórmula al cuadrilátero AFHB , observando que Γ = α ₂ − α ₁ , y realizando la integral sobre φ se obtiene

${\displaystyle S_{12}=R_{2}^{2}(\alpha _{2}-\alpha _{1})+b^{2}\int _{\lambda _{1}}^{\lambda _{2}}\left({\frac {1}{2{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}}}+{\frac {\tanh ^{-1}(e\sin \varphi )}{2e\sin \varphi }}-{\frac {R_{2}^{2}}{b^{2}}}\right)\sin \varphi \,d\lambda ,}$

donde la integral está sobre la línea geodésica (de modo que φ es implícitamente una función de λ ). La integral se puede expresar como una serie válida para f pequeña (Danielsen 1989) (Karney 2013, §6 y apéndice).

El área de un polígono geodésico se obtiene sumando S ₁₂ sobre sus bordes. Este resultado es válido siempre que el polígono no incluya un polo; si es así, se debe sumar 2 π R ₂ ^{2 a la suma.} Si las aristas están especificadas por sus vértices, entonces una expresión conveniente para el exceso geodésico E ₁₂ = α ₂ − α ₁ es

${\displaystyle \tan {\frac {E_{12}}{2}}={\frac {\sin {\tfrac {1}{2}}(\beta _{2}+\beta _{1})}{\cos {\tfrac {1}{2}}(\beta _{2}-\beta _{1})}}\tan {\frac {\omega _{12}}{2}}.}$

Solución de los problemas directo e inverso.

Resolver los problemas geodésicos implica mapear la geodésica en la esfera auxiliar y resolver el problema correspondiente en la navegación de círculo máximo . Al resolver el triángulo esférico "elemental" para NEP en la Fig. 5, se pueden emplear las reglas de Napier para triángulos cuadrantales .

${\displaystyle {\begin{aligned}\sin \alpha _{0}&=\sin \alpha \cos \beta =\tan \omega \cot \sigma ,\\\cos \sigma &=\cos \beta \cos \omega =\tan \alpha _{0}\cot \alpha ,\\\cos \alpha &=\cos \omega \cos \alpha _{0}=\cot \sigma \tan \beta ,\\\sin \beta &=\cos \alpha _{0}\sin \sigma =\cot \alpha \tan \omega ,\\\sin \omega &=\sin \sigma \sin \alpha =\tan \beta \tan \alpha _{0}.\end{aligned}}}$

El mapeo de la geodésica implica evaluar las integrales para la distancia, s , y la longitud, λ , Ecs. (3) y (4) y estos dependen del parámetro α ₀ .

Manejar el problema directo es sencillo, porque α ₀ se puede determinar directamente a partir de las cantidades dadas φ ₁ y α ₁ ; para ver un ejemplo de cálculo, consulte Karney (2013).

En el caso del problema inverso, se da λ _{12 ;} esto no se puede relacionar fácilmente con el ángulo esférico equivalente ω ₁₂ porque se desconoce α ₀ . Por lo tanto, la solución del problema requiere que α ₀ se encuentre iterativamente ( búsqueda de raíz ); ver Karney (2013) para más detalles.

En aplicaciones geodésicas, donde f es pequeña, las integrales normalmente se evalúan como una serie (Legendre 1806) (Oriani 1806) (Bessel 1825) (Helmert 1880) (Rainsford 1955) (Rapp 1993). Para f arbitraria , las integrales (3) y (4) se pueden encontrar mediante cuadratura numérica o expresándolas en términos de integrales elípticas (Legendre 1806) (Cayley 1870) (Karney 2024).

Vincenty (1975) proporciona soluciones para los problemas directo e inverso; Estos se basan en una expansión en serie realizada hasta el tercer orden en el aplanamiento y proporcionan una precisión de aproximadamente0,1 mm para el elipsoide WGS84 ; sin embargo, el método inverso no logra converger en puntos casi antípodas.

Karney (2013) continúa las expansiones al sexto orden, que es suficiente para proporcionar precisión doble completa para | f | ≤ 1 ⁄ 50 y mejora la solución del problema inverso para que converja en todos los casos. Karney (2013, anexo) amplía el método para utilizar integrales elípticas que se pueden aplicar a elipsoides con aplanamiento arbitrario.

Geodésicas sobre un elipsoide triaxial

Resolver el problema geodésico para un elipsoide de revolución es matemáticamente sencillo: debido a la simetría, las geodésicas tienen una constante de movimiento , dada por la relación de Clairaut que permite reducir el problema a cuadratura . A principios del siglo XIX (con el trabajo de Legendre , Oriani , Bessel , et al.), había una comprensión completa de las propiedades de las geodésicas sobre un elipsoide de revolución.

Por otro lado, las geodésicas sobre un elipsoide triaxial (con tres ejes desiguales) no tienen una constante obvia de movimiento y, por lo tanto, representaron un problema desafiante sin resolver en la primera mitad del siglo XIX. En un artículo notable, Jacobi (1839) descubrió una constante del movimiento que permitía reducir este problema también a la cuadratura (Klingenberg 1982, §3.5). ^[4]

Sistema de coordenadas elipsoide triaxial

Fig. 17. Coordenadas elipsoidales triaxiales.

Considere el elipsoide definido por

${\displaystyle h={\frac {X^{2}}{a^{2}}}+{\frac {Y^{2}}{b^{2}}}+{\frac {Z^{2}}{c^{2}}}=1,}$

donde ( X , Y , Z ) son coordenadas cartesianas centradas en el elipsoide y, sin pérdida de generalidad, a ≥ b ≥ c > 0 . ^[5]Jacobi (1866, §§26-27) empleó las coordenadas elipsoidales (triaxiales) (con latitud elipsoidal triaxial y longitud elipsoidal triaxial , β , ω ) definidas por

${\displaystyle {\begin{aligned}X&=a\cos \omega {\frac {\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {a^{2}-c^{2}}}},\\Y&=b\cos \beta \sin \omega ,\\Z&=c\sin \beta {\frac {\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {a^{2}-c^{2}}}}.\end{aligned}}}$

En el límite b → a , β se convierte en la latitud paramétrica para un elipsoide achatado, por lo que el uso del símbolo β es consistente con las secciones anteriores. Sin embargo, ω es diferente de la longitud esférica definida anteriormente. ^[6]

En la Fig. 17 se muestran líneas de cuadrícula de constante β (en azul) y ω (en verde). Éstas constituyen un sistema de coordenadas ortogonal : las líneas de cuadrícula se cruzan en ángulos rectos. Las secciones principales del elipsoide, definidas por X = 0 y Z = 0 , se muestran en rojo. La tercera sección principal, Y = 0 , está cubierta por las líneas β = ±90° y ω = 0° o ±180° . Estas líneas se encuentran en cuatro puntos umbilicales (dos de los cuales son visibles en esta figura) donde los radios principales de curvatura son iguales. Aquí y en las otras figuras de esta sección los parámetros del elipsoide son a : b : c = 1.01:1:0.8 , y se ve en una proyección ortográfica desde un punto por encima de φ = 40° , λ = 30° .

Las líneas de la cuadrícula de las coordenadas elipsoidales se pueden interpretar de tres maneras diferentes:

1. Son "líneas de curvatura" en el elipsoide: son paralelas a las direcciones de curvatura principal (Monge 1796).
2. También son intersecciones del elipsoide con sistemas confocales de hiperboloides de una y dos láminas (Dupin 1813, Parte 5).
3. Finalmente son elipses e hipérbolas geodésicas definidas utilizando dos puntos umbilicales adyacentes (Hilbert & Cohn-Vossen 1952, p. 188). Por ejemplo, las líneas de constante β en la figura 17 se pueden generar con la conocida construcción de cuerdas para elipses con los extremos de la cuerda fijados a los dos puntos umbilicales.

La solución de Jacobi

Jacobi demostró que las ecuaciones geodésicas, expresadas en coordenadas elipsoidales, son separables. Así le contó su descubrimiento a su amigo y vecino Bessel (Jacobi 1839, Carta a Bessel):

Anteayer reduje a cuadratura el problema de las líneas geodésicas en un elipsoide de tres ejes desiguales . Son las fórmulas más simples del mundo, las integrales abelianas , que se convierten en las conocidas integrales elípticas si se igualan 2 ejes.

Königsberg , 28 de diciembre del 38.

La solución dada por Jacobi (Jacobi 1839) (Jacobi 1866, §28) es

${\displaystyle {\begin{aligned}\delta &=\int {\frac {{\sqrt {b^{2}\sin ^{2}\beta +c^{2}\cos ^{2}\beta }}\,d\beta }{{\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {{\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta -\gamma }}}}\\[6pt]&\quad -\int {\frac {{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega }}\,d\omega }{{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {{\bigl (}a^{2}-b^{2}{\bigr )}\sin ^{2}\omega +\gamma }}}}.\end{aligned}}}$

Como señala Jacobi, "una función del ángulo β es igual a una función del ángulo ω . Estas dos funciones son simplemente integrales abelianas..." En la solución aparecen dos constantes δ y γ . Normalmente δ es cero si los límites inferiores de las integrales se toman como el punto de partida de la geodésica y la dirección de las geodésicas está determinada por γ . Sin embargo, para geodésicas que comienzan en puntos umbilicales, tenemos γ = 0 y δ determina la dirección en el punto umbilical. La constante γ se puede expresar como

${\displaystyle \gamma ={\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta \sin ^{2}\alpha -{\bigl (}a^{2}-b^{2}{\bigl )}\sin ^{2}\omega \cos ^{2}\alpha ,}$

donde α es el ángulo que forma la geodésica con las líneas de constante ω . En el límite b → a , esto se reduce a sinα cos β = const. , la familiar relación de Clairaut. Darboux (1894, §§583-584) da una derivación del resultado de Jacobi; Da la solución encontrada por Liouville (1846) para superficies cuadráticas generales.

Levantamiento de geodésicas triaxiales.

Geodésicas circumpolares, ω ₁ =0° , α ₁ =90° .

En un elipsoide triaxial, sólo hay tres geodésicas cerradas simples, las tres secciones principales del elipsoide dadas por X = 0 , Y = 0 y Z = 0 . ^[7] Para estudiar las otras geodésicas, es conveniente considerar geodésicas que intersectan la sección principal media, Y = 0 , en ángulo recto. Estas geodésicas se muestran en las Figs. 18-22, que utilizan los mismos parámetros de elipsoide y la misma dirección de visión que la Fig. 17. Además, las tres elipses principales se muestran en rojo en cada una de estas figuras.

Si el punto de partida es β ₁ ∈ (−90°, 90°) , ω ₁ = 0 y α ₁ = 90° , entonces γ > 0 y la geodésica rodea el elipsoide en un sentido "circumpolar". La geodésica oscila al norte y al sur del ecuador; en cada oscilación completa algo menos que un circuito completo alrededor del elipsoide, lo que da como resultado, en el caso típico, que la geodésica llene el área delimitada por las dos líneas de latitud β = ± β ₁ . En las Figs. 18 y 19. La Figura 18 muestra prácticamente el mismo comportamiento que para un elipsoide de revolución achatado (porque a ≈ b ); compárese con la Fig. 9. Sin embargo, si el punto de partida está en una latitud más alta (Fig. 18), las distorsiones resultantes de a ≠ b son evidentes. Todas las tangentes a una geodésica circumpolar tocan el hiperboloide confocal de una sola hoja que cruza el elipsoide en β = β ₁ (Chasles 1846) (Hilbert y Cohn-Vossen 1952, págs. 223-224).

Geodésicas transpolares, β ₁ =90 ° , α1 ₌180° .

Si el punto de partida es β ₁ = 90° , ω ₁ ∈ (0°, 180°) y α ₁ = 180° , entonces γ < 0 y la geodésica rodea el elipsoide en un sentido "transpolar". La geodésica oscila al este y al oeste de la elipse X = 0 ; en cada oscilación completa un poco más que un circuito completo alrededor del elipsoide. En el caso típico, esto da como resultado que la geodésica llene el área delimitada por las dos líneas de longitud ω = ω ₁ y ω = 180° − ω ₁ . Si a = b , todos los meridianos son geodésicos; el efecto de a ≠ b hace que dichas geodésicas oscilen de este a oeste. En las Figs. 20 y 21. La constricción de la geodésica cerca del polo desaparece en el límite b → c ; en este caso, el elipsoide se convierte en un elipsoide alargado y la Fig. 20 se parecería a la Fig. 10 (girada de lado). Todas las tangentes a una geodésica transpolar tocan el hiperboloide confocal de doble hoja que cruza el elipsoide en ω = ω ₁ .

Fig. 22. Una geodésica umbilical, β ₁ =90 ° , ω1 ₌0° , α ₁ =135° .

Si el punto de partida es β ₁ = 90° , ω ₁ = 0° (un punto umbilical) y α ₁ = 135° (la geodésica deja la elipse Y = 0 en ángulo recto), entonces γ = 0 y la geodésica repetidamente cruza el punto umbilical opuesto y regresa a su punto inicial. Sin embargo, en cada circuito el ángulo en el que se cruza con Y = 0 se acerca más a0° o180° de modo que asintóticamente la geodésica se encuentre en la elipse Y = 0 (Hart 1849) (Arnold 1989, p. 265), como se muestra en la Fig. 22. Una sola geodésica no llena un área en el elipsoide. Todas las tangentes a las geodésicas umbilicales tocan la hipérbola confocal que cruza el elipsoide en los puntos umbilicales.

La geodésica umbilical disfruta de varias propiedades interesantes.

• Por cualquier punto del elipsoide pasan dos geodésicas umbilicales.
• La distancia geodésica entre puntos umbilicales opuestos es la misma independientemente de la dirección inicial de la geodésica.
• Mientras que las geodésicas cerradas en las elipses X = 0 y Z = 0 son estables (una geodésica inicialmente cercana y casi paralela a la elipse permanece cerca de la elipse), la geodésica cerrada en la elipse Y = 0 , que pasa por los 4 puntos umbilicales, es exponencialmente inestable . Si se perturba, saldrá del avión Y = 0 y girará antes de volver a acercarse al avión. (Este comportamiento puede repetirse dependiendo de la naturaleza de la perturbación inicial).

Si el punto de partida A de una geodésica no es un punto umbilical, su envoltura es una astroide con dos cúspides situadas en β = − β ₁ y las otras dos en ω = ω ₁ + π . El lugar de corte para A es la porción de la línea β = − β ₁ entre las cúspides.

Aplicaciones

Los problemas geodésicos directos e inversos ya no desempeñan en la geodesia el papel central que alguna vez desempeñaron. En lugar de resolver el ajuste de redes geodésicas como un problema bidimensional en trigonometría esferoidal, estos problemas ahora se resuelven mediante métodos tridimensionales (Vincenty y Bowring 1978). Sin embargo, las geodésicas terrestres siguen desempeñando un papel importante en varios ámbitos:

• para medir distancias y áreas en sistemas de información geográfica ;
• la definición de fronteras marítimas (UNCLOS 2006);
• en las normas de la Administración Federal de Aviación para la navegación de área (RNAV 2007);
• el método de medición de distancias en el Código Deportivo FAI (FAI 2018).
• ayudar a los musulmanes a encontrar su dirección hacia La Meca

Según el principio de acción mínima , muchos problemas de física pueden formularse como un problema variacional similar al de las geodésicas. De hecho, el problema geodésico es equivalente al movimiento de una partícula obligada a moverse en la superficie, pero por lo demás no sujeta a fuerzas (Laplace 1799a) (Hilbert y Cohn-Vossen 1952, p. 222). Por esta razón, las geodésicas sobre superficies simples como elipsoides de revolución o elipsoides triaxiales se utilizan con frecuencia como "casos de prueba" para explorar nuevos métodos. Ejemplos incluyen:

• el desarrollo de integrales elípticas (Legendre 1811) y funciones elípticas (Weierstrass 1861);
• el desarrollo de la geometría diferencial (Gauss 1828) (Christoffel 1869);
• métodos para resolver sistemas de ecuaciones diferenciales mediante un cambio de variables independientes (Jacobi 1839);
• el estudio de las cáusticas (Jacobi 1891);
• investigaciones sobre el número y la estabilidad de órbitas periódicas (Poincaré 1905);
• en el límite c → 0 , las geodésicas sobre un elipsoide triaxial se reducen a un caso de billar dinámico ;
• extensiones a un número arbitrario de dimensiones (Knörrer 1980);
• flujo geodésico en una superficie (Berger 2010, Capítulo 12).

Ver también

• Caminos de sección de tierra
• figura de la tierra
• Distancia geográfica
• Navegación en círculo máximo
• Gran elipse
• Geodésico
• Geodesia
• Proyección de mapas
  • Proyección cartográfica del elipsoide triaxial.
• arco meridiano
• Línea de rumbo
• Las fórmulas de Vincenty

Notas

1. Aquí α ₂ es el acimut directo en B. En cambio , algunos autores calculan el azimut posterior ; esto viene dado por α ₂ ± π .
2. Laplace (1799a) demostró que una partícula obligada a moverse sobre una superficie pero que por lo demás no está sujeta a fuerzas se mueve a lo largo de una geodésica para esa superficie. Por tanto, la relación de Clairaut es sólo una consecuencia de la conservación del momento angular de una partícula sobre una superficie de revolución.
3. Bagratuni (1962, §17) utiliza el término "coeficiente de convergencia de ordenadas" para la escala geodésica.
4. Esta sección está adaptada de la documentación de GeographicLib (Karney 2015, Geodésicas en un elipsoide triaxial)
5. Esta notación para los semiejes es incompatible con la utilizada en la sección anterior sobre elipsoides de revolución en la que a y b representan el radio ecuatorial y el semieje polar. Por tanto, las desigualdades correspondientes son a = a ≥ b > 0 para un elipsoide achatado y b ≥ a = a > 0 para un elipsoide alargado.
6. El límite b → c da un elipsoide alargado en el que ω desempeña el papel de latitud paramétrica.
7. Si c ⁄ a < 1 ⁄ 2 , existen otras geodésicas cerradas simples similares a las que se muestran en las Figs. 11 y 12 (Klingenberg 1982, §3.5.19).

Referencias

• Arnold, VI (1989). Métodos Matemáticos de la Mecánica Clásica . Traducido por Vogtmann, K.; Weinstein, A. (2ª ed.). Springer-Verlag. ISBN 978-0-387-96890-2. OCLC  4037141.
• Bagratuni, GV (1967) [1962]. Curso de Geodesia Esferoidal . doi :10.5281/zenodo.32371. OCLC  6150611.Traducción del ruso de Курс сфероидической геодезии (Moscú, 1962) por la Fuerza Aérea de EE. UU. (FTD-MT-64-390)
• Berger, M. (2010). Geometría revelada . Traducido por Senechal, LJ Springer. doi :10.1007/978-3-540-70997-8. ISBN 978-3-540-70996-1.
• Bessel, FW (2010) [1825]. "El cálculo de longitud y latitud a partir de mediciones geodésicas". Astronomische Nachrichten . 331 (8). Traducido por Karney, CFF; Deakin, RE: 852–861. arXiv : 0908.1824 . Código Bib : 2010AN....331..852K. doi :10.1002/asna.201011352. S2CID  118760590.Traducción al inglés de Astron. Nachr. 4, 241–254 (1825). Erratas.
• Bliss, GA (1916). "Condición de Jacobi para problemas de cálculo de variaciones en forma paramétrica". Transacciones de la Sociedad Matemática Estadounidense . 17 (2): 195–206. doi : 10.1090/S0002-9947-1916-1501037-4 .
• Bomford, G. (1952). Geodesia . Oxford: Clarendon. OCLC  1396190.
• Borré, K.; Strang, Grupo de Trabajo (2012). "11, Geometría del elipsoide" (PDF) . Algoritmos de Posicionamiento Global . Prensa de Wellesley-Cambridge. ISBN 978-0-9802327-3-8. OCLC  795014501.
• Cayley, A. (1870). "Sobre las líneas geodésicas de un esferoide achatado". Revista Filosófica . 4ta serie. 40 (268): 329–340. doi :10.1080/14786447008640411.
• Chasles, M. (1846). "Sur les lignes géodésiques et les lignes de courbure des Surfaces du second degré" [Líneas geodésicas y líneas de curvatura de las superficies de segundo grado]. Journal de Mathématiques Pures et Appliquées (en francés). 11 : 5–20.PDF.
• Christoffel, EB (1869). "Allgemeine Theorie der geodätischen Dreiecke" [Teoría general de los triángulos geodésicos]. Abhandlungen Königlichen Akademie der Wissenschaft zu Berlin (en alemán): 119-176.
• Claraut, AC (1735). "Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini" [Determinación geométrica de la perpendicular al meridiano dibujada por Jacques Cassini]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (en francés): 406–416.
• Danielsen, JS (1989). "El área bajo la geodésica". Revisión de la encuesta . 30 (232): 61–66. doi :10.1179/003962689791474267.
• Darboux, JG (1894). Leçons sur la théorie générale des Surfaces [ Lecciones sobre teoría general de superficies ] (en francés). vol. 3. París: Gauthier-Villars. OCLC  8566228.
• Dupin, PCF (1813). Développements de Géométrie [ Desarrollos en geometría ] (en francés). París: Courcier. OCLC  560800801.
• Ehlert, D. (1993). Methoden der ellipsoidischen Dreiecksberechnung [ Métodos de triangulación elipsoidal ] (Informe técnico). Reihe B: Angewandte Geodäsie, Heft Nr. 292 (en alemán). Comisión Geodätische Alemana. OCLC  257615376.
• Euler, L. (1755). "Élémens de la trigonométrie sphéroïdique tirés de la méthode des plus grands et plus petits" [Elementos de trigonometría esferoidal tomados del método de máximos y mínimos]. Mémoires de l'Académie Royale des Sciences de Berlin 1753 (en francés). 9 : 258–293.Cifras.
• FAI (2018). "Sección 8.2.3". Código deportivo FAI (PDF) (Informe técnico). Lausana, Suiza: Fédération Aéronautique Internationale.
• Forsyth, AR (1927). Cálculo de variaciones . Universidad de Cambridge. Prensa. ISBN 978-1-107-64083-2. OCLC  250050479.
• Gan'shin, VV (1969) [1967]. Geometría del Elipsoide Terrestre . Traducido por Willis, JM St. Louis: Centro de información y cartas aeronáuticas. doi :10.5281/zenodo.32854. OCLC  493553.Traducción del ruso de Геометрия земного эллипсоида (Moscú, 1967).
• Gauss, CF (1902) [1828]. Investigaciones generales de superficies curvas de 1827 y 1825. Traducido por Morehead, JC; Hiltebeitel, AM Universidad de Princeton. Lib. OCLC  7824448.PDF. Traducción al inglés de Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828).
• Hart, AS (1849). "Demostración geométrica de algunas propiedades de las líneas geodésicas". Revista matemática de Cambridge y Dublín . 4 : 80–84.
• Helmert, FR (1964) [1880]. Teorías Matemáticas y Físicas de la Geodesia Superior . vol. 1. St. Louis: Centro de información y cartas aeronáuticas. doi :10.5281/zenodo.32050. OCLC  17273288.Traducción al inglés de Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, vol. 1 (Teubner, Leipzig, 1880).
• Hilbert, D .; Cohn-Vossen, S. (1952). Geometría y la Imaginación . Traducido por Nemenyi, P. Nueva York: Chelsea. ISBN 9780828400879. OCLC  301610346.
• Hutton, C. (1811). Un curso de matemáticas en tres volúmenes compuesto para uso de la Real Academia Militar. vol. 3. Londres: FC y J. Rivington. OCLC  18031510.
• Jacobi, CGJ (1837). "Zur Theorie der Variations-Rechnung und der Differential-Gleichungen" [La teoría del cálculo de variaciones y de ecuaciones diferenciales]. Journal für die Reine und Angewandte Mathematik (en alemán). 1837 (17): 68–82. doi :10.1515/crll.1837.17.68. S2CID  119469290.
• Jacobi, CGJ (1839). "Note von der geodätischen Linie auf einem Ellipsoid und den verschiedenen Anwendungen einer merkwürdigen analytischen Substitution" [La geodésica sobre un elipsoide y diversas aplicaciones de una notable sustitución analítica]. Journal für die Reine und Angewandte Mathematik (en alemán). 1839 (19): 309–313. doi :10.1515/crll.1839.19.309. S2CID  121670851.Carta a Bessel, 28 de diciembre de 1838. Traducción al francés (1841).
• Jacobi, CGJ (2009) [1866]. A. Clebsch (ed.). Conferencias sobre dinámica . Traducido por Balagangadharan, K. Nueva Delhi: Hindustan Book Agency. ISBN 978-81-85931-91-3. SEÑOR  2569315. OCLC  440645889.Traducción al inglés de Vorlesungen über Dynamik (Reimer, Berlín, 1866). Erratas.
• Jacobi, CGJ (1891). "Über die Curve, welche alle von einem Punkte ausgehenden geodätischen Linien eines Rotationsellipsoides berührt" [La envoltura de líneas geodésicas que emanan de un solo punto en un elipsoide]. En KTW Weierstrass (ed.). Gesammelte Werke de Jacobi (en alemán). vol. 7. Berlín: Reimer. págs. 72–87. OCLC  630416023.op. post., completado por FHA Wangerin . PDF.
• Jekeli, C. (2012), Sistemas de referencia geométrica en geodesia , Universidad Estatal de Ohio, hdl :1811/51274
• Jordania, W .; Eggert, O. (1962) [1941]. Manual de geodesia . vol. 3. Traducido por Carta, MW Washington, DC: Army Map Service. Código Bib : 1962hage.book.....J. doi :10.5281/zenodo.35316. OCLC  34429043.Traducción al inglés del Handbuch der Vermessungskunde , 8.ª edición (Metzler, Stuttgart, 1941).
• Karney, CFF (2013). "Algoritmos para geodésicas". Revista de Geodesia . 87 (1): 43–55. arXiv : 1109.4448 . Código Bib : 2013JGeod..87...43K. doi : 10.1007/s00190-012-0578-z .Adenda.
• Karney, CFF (2015). "Libregrafía". Versión 1.44.
• Karney, CFF (2024). "Geodésicas sobre un elipsoide arbitrario de revolución". Revista de Geodesia . 98 (1): 4:1–14. arXiv : 2208.00492 . doi : 10.1007/s00190-023-01813-2 .
• Klingenberg, WPA (1982). Geometría Riemanniana . de Gruyer. ISBN 978-3-11-008673-7. SEÑOR  0666697. OCLC  8476832.
• Knörrer, H. (1980). "Geodésicas sobre el elipsoide". Invenciones Mathematicae . 59 (2): 119-143. Código Bib : 1980 InMat..59..119K. doi :10.1007/BF01390041. S2CID  118792545.
• Krakiwsky, EJ; Thomson, DB (1974), Cálculos de posición geodésica (PDF) , Departamento de Geodesia e Ingeniería Geomática, Apuntes de conferencias, Fredericton, NB: Univ. de Nuevo Brunswick, Bibcode : 1974gpc..libro.....K
• Laplace, PS (1829) [1799a]. "Libro 1, §8". Tratado de Mecánica Celeste . vol. 1. Traducido por Bowditch, N. Boston: Hillard, Gray, Little y Wilkins. OCLC  1294937.
• Laplace, PS (1799b). Traité de Mécanique Céleste [ Tratado de Mecánica Celeste ] (en francés). vol. 2. París: Crapelet. pag. 112. OCLC  25448952.
• Legendre, AM (1806). "Analyse des Triangles tracées sur la Surface d'un sphéroïde" [Análisis de triángulos esferoidales]. Mémoires de l'Institut National de France (en francés) (primer semestre): 130–161.
• Legendre, AM (1811). Exercices de Calcul Intégral sur Divers Ordres de Transcendentes et sur les Quadratures [ Ejercicios de cálculo integral ] (en francés). París: Courcier. OCLC  312469983.
• Leick, A.; Rapoport, L.; Tatarnikov, D. (2015). Topografía por satélite GPS (4ª ed.). Wiley. ISBN 978-1-119-01828-5.
• Liouville, J. (1846). "Sur quelques cas particuliers où les équations du mouvement d'un point matériel peuvent s'intégrer" [Sobre casos especiales en los que se pueden integrar las ecuaciones de movimiento de una partícula puntual]. Journal de Mathématiques Pures et Appliquées (en francés). 11 : 345–378.PDF
• Lyusternik, L. (1964). Caminos más cortos: problemas variacionales . Conferencias populares de matemáticas. vol. 13. Traducido por Collins, P.; Brown, RB Nueva York: Macmillan. SEÑOR  0178386. OCLC  1048605.Traducción del ruso de Кратчайшие Линии: Вариационные Задачи (Moscú, 1955).
• Monge, G. (1850) [1796]. "Sur les lignes de courbure de la Surface de l'ellipsoïde" [Sobre las líneas de curvatura de la superficie del elipsoide]. En J. Liouville (ed.). Application de l'Analyse à la Géometrie (en francés) (5ª ed.). París: Bachiller. págs. 139-160. OCLC  2829112.(Figura 1-2, Figura 3-4). Edición de 1796 (figuras 1-2, figuras 3-4). Figuras en PDF.
• Estudio Geodésico Nacional (2012). "Utilidades geodésicas: inversa y directa". Versión 3.0.
• Newton, I. (1848) [1687]. "Libro 3, Proposición 19, Problema 3". Los principios matemáticos de la filosofía natural . Traducido por Motte, A. Nueva York: Adee. págs. 405–409.Traducción al inglés de Philosophiæ Naturalis Principia Mathematica . Liber Tertius, Proposición XIX. Prob. II. págs. 422–424.
• Oriani, B. (1806). "Elementi di trigonometria sferoidica, Pt. 1" [Elementos de trigonometría esferoidal]. Memorie dell'Istituto Nazionale Italiano (en italiano). 1 (1): 118–198.
• Oriani, B. (1808). "Elementi di trigonometria sferoidica, Pt. 2" [Elementos de trigonometría esferoidal]. Memorie dell'Istituto Nazionale Italiano (en italiano). 2 (1): 1–58.
• Oriani, B. (1810). "Elementi di trigonometria sferoidica, Pt. 3" [Elementos de trigonometría esferoidal]. Memorie dell'Istituto Nazionale Italiano (en italiano). 2 (2): 1–58.
• Poincaré, H. (1905). "Sur les lignes géodésiques des Surfaces convexes" [Líneas geodésicas sobre superficies convexas]. Transacciones de la Sociedad Matemática Estadounidense (en francés). 6 (3): 237–274. doi :10.2307/1986219. JSTOR  1986219.
• Rainsford, HF (1955). "Geodésicas largas sobre el elipsoide". Boletín Geodésique . 37 (1): 12–22. Código Bib : 1955BGeod..29...12R. doi :10.1007/BF02527187. S2CID  122111614.
• Rapp, RH (1991), Geodesia geométrica, parte I , Universidad Estatal de Ohio, hdl :1811/24333
• Rapp, RH (1993), Geodesia geométrica, parte II , Universidad Estatal de Ohio, hdl :1811/24409
• RNAV (2007). "Apéndice 2.". Orden 8260.54A, Estándar de Estados Unidos para navegación de área (PDF) (Reporte técnico). Washington, DC: Administración Federal de Aviación de EE. UU.
• Sjoberg, LE (2006). "Determinación de áreas en el plano, esfera y elipsoide". Revisión de la encuesta . 38 (301): 583–593. doi :10.1179/003962606780732100.
• CONVEMAR (2006). Manual sobre aspectos técnicos de la Convención de las Naciones Unidas sobre el Derecho del Mar, 1982 (PDF) (Informe técnico) (4ª ed.). Mónaco: Oficina Hidrográfica Internacional. Archivado desde el original (PDF) el 24 de mayo de 2013 . Consultado el 15 de agosto de 2013 .
• Vicente, T. (1975). «Soluciones directas e inversas de geodésicas sobre el elipsoide con aplicación de ecuaciones anidadas» (PDF) . Revisión de la encuesta . 23 (176): 88–93. Código Bib : 1975SurRv..23...88V. doi :10.1179/sre.1975.23.176.88. Anexo: Revisión de la encuesta 23 (180): 294 (1976).
• Vicente, T .; Bowring, BR (1978). Aplicación de geodesia tridimensional a ajustes de redes horizontales (PDF) (Reporte técnico). NOAA. NOS NGS-13.
• Weierstrass, KTW (1861). "Über die geodätischen Linien auf dem dreiaxigen Ellipsoid" [Líneas geodésicas en un elipsoide triaxial]. Monatsberichte der Königlichen Akademie der Wissenschaft zu Berlin (en alemán): 986–997.

enlaces externos

• Bibliografía geodésica en línea de libros y artículos sobre geodésicas en elipsoides.
• Conjunto de prueba para geodésicas, un conjunto de 500.000 geodésicas para el elipsoide WGS84, calculadas mediante aritmética de alta precisión.
• Implementación de la herramienta NGS Vincenty (1975).
• geod(1), página de manual de la utilidad PROJ para cálculos geodésicos.
• Implementación de GeographicLib de Karney (2013).
• Dibujar geodésicas en Google Maps.