Integral

Operation in mathematical calculus

Una integral definida de una función se puede representar como el área firmada de la región delimitada por su gráfica y el eje horizontal; en el gráfico anterior como ejemplo, la integral de es el área amarilla (−) restada del área azul (+) ${\displaystyle f(x)}$

En matemáticas , una integral es el análogo continuo de una suma , que se utiliza para calcular áreas , volúmenes y sus generalizaciones. La integración, el proceso de calcular una integral, es una de las dos operaciones fundamentales del cálculo , siendo la otra ^la diferenciación . La integración se utilizó inicialmente para resolver problemas de matemáticas y física , como encontrar el área bajo una curva o determinar el desplazamiento a partir de la velocidad. El uso de la integración se expandió a una amplia variedad de campos científicos a partir de entonces.

Una integral definida calcula el área con signo de la región en el plano que está limitada por la gráfica de una función dada entre dos puntos en la línea real . Convencionalmente, las áreas por encima del eje horizontal del plano son positivas mientras que las áreas por debajo son negativas. Las integrales también se refieren al concepto de antiderivada , una función cuya derivada es la función dada; en este caso, también se denominan integrales indefinidas . El teorema fundamental del cálculo relaciona la integración definida con la diferenciación y proporciona un método para calcular la integral definida de una función cuando se conoce su antiderivada; la diferenciación y la integración son operaciones inversas .

Aunque los métodos de cálculo de áreas y volúmenes datan de las matemáticas de la antigua Grecia , los principios de integración fueron formulados independientemente por Isaac Newton y Gottfried Wilhelm Leibniz a finales del siglo XVII, quienes pensaron en el área bajo una curva como una suma infinita de rectángulos de ancho infinitesimal . Bernhard Riemann dio más tarde una definición rigurosa de integrales, que se basa en un procedimiento limitante que aproxima el área de una región curvilínea al dividir la región en losas verticales infinitesimalmente delgadas. A principios del siglo XX, Henri Lebesgue generalizó la formulación de Riemann al introducir lo que ahora se conoce como la integral de Lebesgue ; es más general que la de Riemann en el sentido de que una clase más amplia de funciones son integrables mediante Lebesgue.

Las integrales pueden generalizarse según el tipo de función y el dominio en el que se realiza la integración. Por ejemplo, una integral de línea se define para funciones de dos o más variables y el intervalo de integración se reemplaza por una curva que conecta dos puntos en el espacio. En una integral de superficie , la curva se reemplaza por un fragmento de una superficie en el espacio tridimensional .

Historia

Integración de precálculo

La primera técnica sistemática documentada capaz de determinar integrales es el método de agotamiento del antiguo astrónomo griego Eudoxo y el filósofo Demócrito ( ca. 370 a. C.), que buscaba encontrar áreas y volúmenes dividiéndolos en un número infinito de divisiones para las que se conocía el área o el volumen. ^[1] Este método fue desarrollado y empleado por Arquímedes en el siglo III a. C. y se utilizó para calcular el área de un círculo , el área superficial y el volumen de una esfera , el área de una elipse , el área bajo una parábola , el volumen de un segmento de un paraboloide de revolución, el volumen de un segmento de un hiperboloide de revolución y el área de una espiral . ^[2]

Un método similar fue desarrollado independientemente en China alrededor del siglo III d. C. por Liu Hui , quien lo utilizó para hallar el área del círculo. Este método fue utilizado más tarde en el siglo V por los matemáticos chinos Zu Chongzhi y Zu Geng, padre e hijo, para hallar el volumen de una esfera. ^[3]

En Oriente Medio, Hasan Ibn al-Haytham, latinizado como Alhazen ( c.  965  – c.  1040  d. C.) derivó una fórmula para la suma de cuartas potencias . ^[4] Alhazen determinó las ecuaciones para calcular el área encerrada por la curva representada por (que se traduce a la integral en notación contemporánea), para cualquier valor entero no negativo dado de . ^[5] Utilizó los resultados para llevar a cabo lo que ahora se llamaría una integración de esta función, donde las fórmulas para las sumas de cuadrados integrales y cuartas potencias le permitieron calcular el volumen de un paraboloide . ^[6] ${\displaystyle y=x^{k}}$ ${\displaystyle \int x^{k}\,dx}$ ${\displaystyle k}$

Los siguientes avances significativos en el cálculo integral no comenzaron a aparecer hasta el siglo XVII. En esta época, el trabajo de Cavalieri con su método de indivisibles y el trabajo de Fermat comenzaron a sentar las bases del cálculo moderno, ^[7] con Cavalieri calculando las integrales de x ⁿ hasta el grado n = 9 en la fórmula de cuadratura de Cavalieri . ^[8] El caso n = −1 requirió la invención de una función , el logaritmo hiperbólico , logrado por cuadratura de la hipérbola en 1647.

A principios del siglo XVII, Barrow y Torricelli dieron otros pasos y aportaron los primeros indicios de una conexión entre la integración y la diferenciación . Barrow proporcionó la primera prueba del teorema fundamental del cálculo . ^[9] Wallis generalizó el método de Cavalieri, calculando integrales de x elevadas a una potencia general, incluidas las potencias negativas y las potencias fraccionarias. ^[10]

Leibniz y Newton

El mayor avance en la integración se produjo en el siglo XVII con el descubrimiento independiente del teorema fundamental del cálculo por parte de Leibniz y Newton . ^[11] El teorema demuestra una conexión entre la integración y la diferenciación. Esta conexión, combinada con la relativa facilidad de la diferenciación, puede aprovecharse para calcular integrales. En particular, el teorema fundamental del cálculo permite resolver una clase mucho más amplia de problemas. Igual de importante es el amplio marco matemático que desarrollaron tanto Leibniz como Newton. Dado el nombre de cálculo infinitesimal, permitió un análisis preciso de funciones con dominios continuos. Este marco finalmente se convirtió en el cálculo moderno , cuya notación para integrales se extrae directamente del trabajo de Leibniz.

Formalización

Aunque Newton y Leibniz proporcionaron un enfoque sistemático para la integración, su trabajo carecía de un grado de rigor . El obispo Berkeley atacó memorablemente los incrementos evanescentes utilizados por Newton, llamándolos " fantasmas de cantidades desaparecidas ". ^[12] El cálculo adquirió una base más firme con el desarrollo de los límites . La integración fue formalizada rigurosamente por primera vez, utilizando límites, por Riemann . ^[13] Aunque todas las funciones continuas acotadas por partes son integrables por Riemann en un intervalo acotado, posteriormente se consideraron funciones más generales, particularmente en el contexto del análisis de Fourier , a las que no se aplica la definición de Riemann, y Lebesgue formuló una definición diferente de integral, fundada en la teoría de la medida (un subcampo del análisis real ). Se propusieron otras definiciones de integral, que extendían los enfoques de Riemann y Lebesgue. Estos enfoques basados ​​en el sistema de números reales son los más comunes hoy en día, pero existen enfoques alternativos, como una definición de integral como la parte estándar de una suma infinita de Riemann, basada en el sistema de números hiperreales .

Notación histórica

La notación para la integral indefinida fue introducida por Gottfried Wilhelm Leibniz en 1675. ^[14] Adaptó el símbolo de la integral , ∫ , de la letra ſ ( s larga ), que representa la suma (escrita como ſumma ; en latín significa "suma" o "total"). La notación moderna para la integral definida, con límites por encima y por debajo del signo de la integral, fue utilizada por primera vez por Joseph Fourier en Mémoires de la Academia Francesa alrededor de 1819-1820, reimpresa en su libro de 1822. ^[15]

Isaac Newton utilizó una pequeña barra vertical sobre una variable para indicar la integración, o colocó la variable dentro de un recuadro. La barra vertical se confundía fácilmente con.incógnitao x ′ , que se utilizan para indicar diferenciación, y la notación de caja era difícil de reproducir para los impresores, por lo que estas notaciones no fueron ampliamente adoptadas. ^[16]

Primer uso del término

El término fue impreso por primera vez en latín por Jacob Bernoulli en 1690: "Ergo et horum Integralia aequantur". ^[17]

Terminología y notación

En general, la integral de una función de valor real f ( x ) con respecto a una variable real x en un intervalo [ a , b ] se escribe como

${\displaystyle \int _{a}^{b}f(x)\,dx.}$

El signo integral ∫ representa la integración. El símbolo dx , llamado diferencial de la variable x , indica que la variable de integración es x . La función f ( x ) se llama integrando, los puntos a y b se llaman límites (o acotaciones) de integración y se dice que la integral está sobre el intervalo [ a , b ] , llamado intervalo de integración. ^[18] Se dice que una función es integrableSi su integral sobre su dominio es finita. Si se especifican límites, la integral se denomina integral definida.

Cuando se omiten los límites, como en

${\displaystyle \int f(x)\,dx,}$

La integral se denomina integral indefinida y representa una clase de funciones (la antiderivada ) cuya derivada es el integrando. ^[19] El teorema fundamental del cálculo relaciona la evaluación de integrales definidas con integrales indefinidas. Existen varias extensiones de la notación para integrales que abarcan la integración en dominios ilimitados y/o en múltiples dimensiones (consulte las secciones posteriores de este artículo).

En entornos avanzados, no es raro omitir dx cuando solo se utiliza la integral de Riemann simple o el tipo exacto de integral es irrelevante. Por ejemplo, se podría escribir para expresar la linealidad de la integral, una propiedad compartida por la integral de Riemann y todas sus generalizaciones. ^[20] ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$

Interpretaciones

Aproximaciones a la integral de √ x de 0 a 1, con 5 particiones de extremo derecho amarillas y 10 particiones de extremo izquierdo verdes

Las integrales aparecen en muchas situaciones prácticas. Por ejemplo, a partir de la longitud, el ancho y la profundidad de una piscina rectangular con un fondo plano, se puede determinar el volumen de agua que puede contener, el área de su superficie y la longitud de su borde. Pero si es ovalada con un fondo redondeado, se requieren integrales para encontrar valores exactos y rigurosos para estas cantidades. En cada caso, se puede dividir la cantidad buscada en infinitas partes infinitesimales y luego sumar las partes para lograr una aproximación precisa.

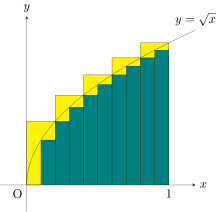
Como otro ejemplo, para encontrar el área de la región limitada por la gráfica de la función f ( x ) = entre x = 0 y x = 1 , se puede dividir el intervalo en cinco partes ( 0, 1/5, 2/5, ..., 1 ), luego construir rectángulos usando la altura del extremo derecho de cada parte (por lo tanto √ 0 , √ 1/5 , √ 2/5 , ..., √ 1 ) y sumar sus áreas para obtener la aproximación ${\textstyle {\sqrt {x}}}$

${\displaystyle \textstyle {\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0.7497,}$

que es mayor que el valor exacto. Alternativamente, al reemplazar estos subintervalos por unos con la altura del extremo izquierdo de cada pieza, la aproximación que se obtiene es demasiado baja: con doce de esos subintervalos, el área aproximada es solo 0,6203. Sin embargo, cuando el número de piezas aumenta hasta el infinito, alcanzará un límite que es el valor exacto del área buscada (en este caso, 2/3 ). Se escribe

${\displaystyle \int _{0}^{1}{\sqrt {x}}\,dx={\frac {2}{3}},}$

lo que significa que 2/3 es el resultado de una suma ponderada de valores de función, √ x , multiplicada por los anchos de paso infinitesimales, denotados por dx , en el intervalo [0, 1] .

Sumas de Darboux

Definiciones formales

Existen muchas formas de definir formalmente una integral, y no todas son equivalentes. Las diferencias existen principalmente para abordar casos especiales distintos que pueden no ser integrables con otras definiciones, pero también, en ocasiones, por razones pedagógicas. Las definiciones más utilizadas son las integrales de Riemann y las integrales de Lebesgue.

Integral de Riemann

La integral de Riemann se define en términos de sumas de funciones de Riemann con respecto a particiones etiquetadas de un intervalo. ^[21] Una partición etiquetada de un intervalo cerrado [ a , b ] en la línea real es una secuencia finita

${\displaystyle a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!}$

Esto divide el intervalo [ a , b ] en n subintervalos [ x _{i −1} , x _i ] indexados por i , cada uno de los cuales está "etiquetado" con un punto específico t _i ∈ [ x _{i −1} , x _i ] . Una suma de Riemann de una función f con respecto a dicha partición etiquetada se define como

${\displaystyle \sum _{i=1}^{n}f(t_{i})\,\Delta _{i};}$

Así, cada término de la suma es el área de un rectángulo con una altura igual al valor de la función en el punto elegido del subintervalo dado, y un ancho igual al ancho del subintervalo, Δ _i = x _i − x _{i −1} . La malla de dicha partición etiquetada es el ancho del subintervalo más grande formado por la partición, max _{i =1... n} Δ _i . La integral de Riemann de una función f en el intervalo [ a , b ] es igual a S si: ^[22]

Para todo existe tal que, para cualquier partición etiquetada con malla menor que , ${\displaystyle \varepsilon >0}$ ${\displaystyle \delta >0}$ ${\displaystyle [a,b]}$ ${\displaystyle \delta }$

${\displaystyle \left|S-\sum _{i=1}^{n}f(t_{i})\,\Delta _{i}\right|<\varepsilon .}$

Cuando las etiquetas elegidas son el valor máximo (respectivamente, mínimo) de la función en cada intervalo, la suma de Riemann se convierte en una suma de Darboux superior (respectivamente, inferior) , lo que sugiere la estrecha conexión entre la integral de Riemann y la integral de Darboux .

Integral de Lebesgue

Integración de Lebesgue

A menudo resulta interesante, tanto en teoría como en aplicaciones, poder pasar al límite bajo la integral. Por ejemplo, con frecuencia se puede construir una secuencia de funciones que se aproximen, en un sentido adecuado, a la solución de un problema. En ese caso, la integral de la función solución debería ser el límite de las integrales de las aproximaciones. Sin embargo, muchas funciones que se pueden obtener como límites no son integrables en Riemann, por lo que dichos teoremas de límite no se cumplen con la integral de Riemann. Por lo tanto, es de gran importancia tener una definición de la integral que permita integrar una clase más amplia de funciones. ^[23]

Una de estas integrales es la integral de Lebesgue, que aprovecha el siguiente hecho para ampliar la clase de funciones integrables: si los valores de una función se reordenan en el dominio, la integral de una función debería permanecer igual. Así, Henri Lebesgue introdujo la integral que lleva su nombre, explicándola de esta manera en una carta a Paul Montel : ^[24]

Tengo que pagar una cierta cantidad de dinero que he acumulado en mi bolsillo. Saco los billetes y monedas de mi bolsillo y se los doy al acreedor en el orden en que los encuentro hasta que alcanzo la suma total. Esta es la integral de Riemann. Pero puedo proceder de otra manera. Después de haber sacado todo el dinero de mi bolsillo, ordeno los billetes y monedas según valores idénticos y luego pago los varios montones uno tras otro al acreedor. Esta es mi integral.

Como dice Folland, "para calcular la integral de Riemann de f , se divide el dominio [ a , b ] en subintervalos", mientras que en la integral de Lebesgue, "se divide en efecto el rango de f ". ^[25] La definición de la integral de Lebesgue comienza con una medida , μ. En el caso más simple, la medida de Lebesgue μ ( A ) de un intervalo A = [ a , b ] es su ancho, b − a , de modo que la integral de Lebesgue concuerda con la integral de Riemann (adecuada) cuando ambas existen. ^[26] En casos más complicados, los conjuntos que se miden pueden estar muy fragmentados, sin continuidad y sin semejanza con los intervalos.

Usando la filosofía de "particionar el rango de f ", la integral de una función no negativa f  : R → R debería ser la suma sobre t de las áreas entre una delgada franja horizontal entre y = t e y = t + dt . Esta área es simplemente μ { x  : f ( x ) > t }  dt . Sea f ^∗ ( t ) = μ { x  : f ( x ) > t } . La integral de Lebesgue de f se define entonces por

${\displaystyle \int f=\int _{0}^{\infty }f^{*}(t)\,dt}$

donde la integral de la derecha es una integral de Riemann impropia ordinaria ( f ^∗ es una función positiva estrictamente decreciente y, por lo tanto, tiene una integral de Riemann impropia bien definida ). ^[27] Para una clase adecuada de funciones (las funciones medibles ) esto define la integral de Lebesgue.

Una función general medible f es integrable según Lebesgue si la suma de los valores absolutos de las áreas de las regiones entre la gráfica de f y el eje x es finita: ^[28]

${\displaystyle \int _{E}|f|\,d\mu <+\infty .}$

En ese caso, la integral es, como en el caso riemanniano, la diferencia entre el área por encima del eje x y el área por debajo del eje x : ^[29]

${\displaystyle \int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu }$

dónde

${\displaystyle {\begin{alignedat}{3}&f^{+}(x)&&{}={}\max\{f(x),0\}&&{}={}{\begin{cases}f(x),&{\text{if }}f(x)>0,\\0,&{\text{otherwise,}}\end{cases}}\\&f^{-}(x)&&{}={}\max\{-f(x),0\}&&{}={}{\begin{cases}-f(x),&{\text{if }}f(x)<0,\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}}$

Otras integrales

Aunque las integrales de Riemann y Lebesgue son las definiciones más utilizadas de la integral, existen otras, entre ellas:

• La integral de Darboux , que se define mediante sumas de Darboux (sumas de Riemann restringidas), es equivalente a la integral de Riemann . Una función es integrable mediante Darboux si y solo si es integrable mediante Riemann. Las integrales de Darboux tienen la ventaja de ser más fáciles de definir que las integrales de Riemann.
• La integral de Riemann-Stieltjes , una extensión de la integral de Riemann que integra con respecto a una función en lugar de una variable.
• La integral de Lebesgue-Stieltjes , desarrollada posteriormente por Johann Radon , que generaliza las integrales de Riemann-Stieltjes y de Lebesgue.
• La integral de Daniell , que subsume la integral de Lebesgue y la integral de Lebesgue-Stieltjes sin depender de medidas .
• La integral de Haar , utilizada para la integración en grupos topológicos localmente compactos, introducida por Alfréd Haar en 1933.
• La integral de Henstock-Kurzweil , definida de diversas formas por Arnaud Denjoy , Oskar Perron y (más elegantemente, como la integral de calibre) Jaroslav Kurzweil , y desarrollada por Ralph Henstock .
• La integral de Itô y la integral de Stratonovich , que definen la integración con respecto a semimartingalas como el movimiento browniano .
• La integral de Young , que es una especie de integral de Riemann-Stieltjes con respecto a ciertas funciones de variación ilimitada .
• La integral de trayectoria aproximada , que se define para funciones equipadas con alguna estructura de "trayectoria aproximada" adicional y generaliza la integración estocástica tanto contra semimartingalas como contra procesos como el movimiento browniano fraccional .
• La integral de Choquet , una integral subaditiva o superaditiva creada por el matemático francés Gustave Choquet en 1953.
• La integral de Bochner , una extensión de la integral de Lebesgue a una clase más general de funciones, es decir, aquellas con un dominio que es un espacio de Banach .

Propiedades

Linealidad

La colección de funciones integrables de Riemann en un intervalo cerrado [ a , b ] forma un espacio vectorial bajo las operaciones de adición y multiplicación puntual por un escalar, y la operación de integración

${\displaystyle f\mapsto \int _{a}^{b}f(x)\;dx}$

es una función lineal en este espacio vectorial. Por lo tanto, la colección de funciones integrables está cerrada tomando combinaciones lineales , y la integral de una combinación lineal es la combinación lineal de las integrales: ^[30]

${\displaystyle \int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,}$

De manera similar, el conjunto de funciones integrables de Lebesgue de valores reales en un espacio de medida dado E con medida μ es cerrado al tomar combinaciones lineales y, por lo tanto, forma un espacio vectorial, y la integral de Lebesgue

${\displaystyle f\mapsto \int _{E}f\,d\mu }$

es una funcional lineal en este espacio vectorial, de modo que: ^[29]

${\displaystyle \int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu .}$

De manera más general, considere el espacio vectorial de todas las funciones mensurables en un espacio de medida ( E , μ ) , que toman valores en un espacio vectorial topológico completo localmente compacto V sobre un campo topológico localmente compacto K , f  : E → V . Luego se puede definir un mapa de integración abstracto asignando a cada función f un elemento de V o el símbolo ∞ ,

${\displaystyle f\mapsto \int _{E}f\,d\mu ,\,}$

que es compatible con combinaciones lineales. ^[31] En esta situación, la linealidad se cumple para el subespacio de funciones cuya integral es un elemento de V (es decir, "finito"). Los casos especiales más importantes surgen cuando K es R , C o una extensión finita del campo Q _p de números p-ádicos , y V es un espacio vectorial de dimensión finita sobre K , y cuando K = C y V es un espacio de Hilbert complejo .

La linealidad, junto con algunas propiedades de continuidad natural y la normalización para una cierta clase de funciones "simples", se pueden utilizar para dar una definición alternativa de la integral. Este es el enfoque de Daniell para el caso de funciones de valores reales en un conjunto X , generalizado por Nicolas Bourbaki a funciones con valores en un espacio vectorial topológico localmente compacto. Véase Hildebrandt 1953 para una caracterización axiomática de la integral.

Desigualdades

Una serie de desigualdades generales son válidas para funciones integrables de Riemann definidas en un intervalo cerrado y acotado [ a , b ] y pueden generalizarse a otras nociones de integral (Lebesgue y Daniell).

• Límites superior e inferior. Una función integrable f en [ a , b ] , está necesariamente acotada en ese intervalo. Por lo tanto, existen números reales m y M tales que m ≤ f  ( x ) ≤ M para todo x en [ a , b ] . Como las sumas inferior y superior de f sobre [ a , b ] están acotadas, respectivamente, por m ( b − a ) y M ( b − a ) , se sigue que $${\displaystyle m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).}$$
• Desigualdades entre funciones. ^[32] Si f ( x ) ≤ g ( x ) para cada x en [ a , b ] entonces cada una de las sumas superior e inferior de f está acotada por encima por las sumas superior e inferior, respectivamente, de g . Por lo tanto Esta es una generalización de las desigualdades anteriores, ya que M ( b − a ) es la integral de la función constante con valor M sobre [ a , b ] . Además, si la desigualdad entre funciones es estricta, entonces la desigualdad entre integrales también es estricta. Es decir, si f ( x ) < g ( x ) para cada x en [ a , b ] , entonces $${\displaystyle \int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.}$$ $${\displaystyle \int _{a}^{b}f(x)\,dx<\int _{a}^{b}g(x)\,dx.}$$
• Subintervalos. Si [ c , d ] es un subintervalo de [ a , b ] y f  ( x ) es no negativo para todo x , entonces $${\displaystyle \int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.}$$
• Productos y valores absolutos de funciones. Si f y g son dos funciones, entonces podemos considerar sus productos puntuales y potencias, y valores absolutos : Si f es integrable en Riemann en [ a , b ] entonces lo mismo es cierto para | f | , y Además, si f y g son ambas integrables en Riemann entonces fg también es integrable en Riemann, y Esta desigualdad, conocida como la desigualdad de Cauchy-Schwarz , juega un papel destacado en la teoría del espacio de Hilbert , donde el lado izquierdo se interpreta como el producto interno de dos funciones integrables al cuadrado f y g en el intervalo [ a , b ] . $${\displaystyle (fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.}$$ $${\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.}$$ $${\displaystyle \left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).}$$
• Desigualdad de Hölder . ^[33] Supóngase que p y q son dos números reales, 1 ≤ p , q ≤ ∞ con ⁠1/pag⁠ + ⁠1/q⁠ = 1 , y f y g son dos funciones integrables de Riemann. Entonces las funciones | f | ^p y | g | ^q también son integrables y se cumple la siguiente desigualdad de Hölder :Para p = q = 2 , la desigualdad de Hölder se convierte en la desigualdad de Cauchy-Schwarz. $${\displaystyle \left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.}$$
• Desigualdad de Minkowski . ^[33] Supóngase que p ≥ 1 es un número real y f y g son funciones integrables en Riemann. Entonces | f | ^p , | g | ^p y | f + g | ^p también son integrables en Riemann y se cumple la siguiente desigualdad de Minkowski : Un análogo de esta desigualdad para la integral de Lebesgue se utiliza en la construcción de espacios L p . $${\displaystyle \left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.}$$

Convenciones

En esta sección, f es una función integrable de Riemann de valor real . La integral

${\displaystyle \int _{a}^{b}f(x)\,dx}$

sobre un intervalo [ a , b ] se define si a < b . Esto significa que las sumas superior e inferior de la función f se evalúan en una partición a = x ₀ ≤ x ₁ ≤ . . . ≤ x _n = b cuyos valores x _i son crecientes. Geométricamente, esto significa que la integración tiene lugar "de izquierda a derecha", evaluándose f dentro de intervalos [ x _i  , x _{i  +1} ] donde un intervalo con un índice más alto se encuentra a la derecha de uno con un índice más bajo. Los valores a y b , los puntos finales del intervalo , se denominan límites de integración de f . Las integrales también se pueden definir si a > b : ^[18]

${\displaystyle \int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.}$

Con a = b , esto implica:

${\displaystyle \int _{a}^{a}f(x)\,dx=0.}$

La primera convención es necesaria para tomar integrales sobre subintervalos de [ a , b ] ; la segunda dice que una integral tomada sobre un intervalo degenerado, o un punto , debe ser cero . Una razón para la primera convención es que la integrabilidad de f en un intervalo [ a , b ] implica que f es integrable en cualquier subintervalo [ c , d ] , pero en particular las integrales tienen la propiedad de que si c es cualquier elemento de [ a , b ] , entonces: ^[30]

${\displaystyle \int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.}$

Con la primera convención, la relación resultante

${\displaystyle {\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}}$

queda entonces bien definido para cualquier permutación cíclica de a , b y c .

Teorema fundamental del cálculo

El teorema fundamental del cálculo es la afirmación de que la diferenciación y la integración son operaciones inversas: si una función continua se integra primero y luego se diferencia, se recupera la función original. ^[34] Una consecuencia importante, a veces llamada el segundo teorema fundamental del cálculo , permite calcular integrales utilizando una antiderivada de la función a integrar. ^[35]

Primer teorema

Sea f una función continua de valor real definida en un intervalo cerrado [ a , b ] . Sea F la función definida, para todo x en [ a , b ] , por ^[36]

${\displaystyle F(x)=\int _{a}^{x}f(t)\,dt.}$

Entonces, F es continua en [ a , b ] , diferenciable en el intervalo abierto ( a , b ) , y

${\displaystyle F'(x)=f(x)}$

para todo x en ( a , b ) .

Segundo teorema

Sea f una función de valor real definida en un intervalo cerrado [ a , b ] que admite una antiderivada F en [ a , b ] . Es decir, f y F son funciones tales que para todo x en [ a , b ] ,

${\displaystyle f(x)=F'(x).}$

Si f es integrable en [ a , b ] entonces

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}$

Extensiones

Integrales impropias

La integral impropia tiene intervalos ilimitados tanto para el dominio como para el rango. ${\displaystyle \int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi }$

Una integral de Riemann "adecuada" supone que el integrando está definido y es finito en un intervalo cerrado y acotado, delimitado por los límites de integración. Una integral impropia se produce cuando una o más de estas condiciones no se satisfacen. En algunos casos, dichas integrales pueden definirse considerando el límite de una secuencia de integrales de Riemann adecuadas en intervalos progresivamente mayores.

Si el intervalo no está acotado, por ejemplo en su extremo superior, entonces la integral impropia es el límite ya que ese punto final tiende al infinito: ^[37]

${\displaystyle \int _{a}^{\infty }f(x)\,dx=\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx.}$

Si el integrando sólo está definido o es finito en un intervalo semiabierto, por ejemplo ( a , b ] , entonces nuevamente un límite puede proporcionar un resultado finito: ^[38]

${\displaystyle \int _{a}^{b}f(x)\,dx=\lim _{\varepsilon \to 0}\int _{a+\epsilon }^{b}f(x)\,dx.}$

Es decir, la integral impropia es el límite de las integrales propias cuando un extremo del intervalo de integración se aproxima a un número real especificado , o ∞ , o −∞ . En casos más complicados, se requieren límites en ambos extremos o en puntos interiores.

Integración múltiple

La integral doble calcula el volumen bajo una superficie ${\displaystyle z=f(x,y)}$

Just as the definite integral of a positive function of one variable represents the area of the region between the graph of the function and the x-axis, the double integral of a positive function of two variables represents the volume of the region between the surface defined by the function and the plane that contains its domain.^[39] For example, a function in two dimensions depends on two real variables, x and y, and the integral of a function f over the rectangle R given as the Cartesian product of two intervals ${\displaystyle R=[a,b]\times [c,d]}$ can be written

${\displaystyle \int _{R}f(x,y)\,dA}$

where the differential dA indicates that integration is taken with respect to area. This double integral can be defined using Riemann sums, and represents the (signed) volume under the graph of z = f(x,y) over the domain R.^[40] Under suitable conditions (e.g., if f is continuous), Fubini's theorem states that this integral can be expressed as an equivalent iterated integral^[41]

${\displaystyle \int _{a}^{b}\left[\int _{c}^{d}f(x,y)\,dy\right]\,dx.}$

This reduces the problem of computing a double integral to computing one-dimensional integrals. Because of this, another notation for the integral over R uses a double integral sign:^[40]

${\displaystyle \iint _{R}f(x,y)\,dA.}$

Integration over more general domains is possible. The integral of a function f, with respect to volume, over an n-dimensional region D of ${\displaystyle \mathbb {R} ^{n}}$ is denoted by symbols such as:

${\displaystyle \int _{D}f(\mathbf {x} )d^{n}\mathbf {x} \ =\int _{D}f\,dV.}$

Line integrals and surface integrals

A line integral sums together elements along a curve.

The concept of an integral can be extended to more general domains of integration, such as curved lines and surfaces inside higher-dimensional spaces. Such integrals are known as line integrals and surface integrals respectively. These have important applications in physics, as when dealing with vector fields.

A line integral (sometimes called a path integral) is an integral where the function to be integrated is evaluated along a curve.^[42] Various different line integrals are in use. In the case of a closed curve it is also called a contour integral.

The function to be integrated may be a scalar field or a vector field. The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length or, for a vector field, the scalar product of the vector field with a differential vector in the curve).^[43] This weighting distinguishes the line integral from simpler integrals defined on intervals. Many simple formulas in physics have natural continuous analogs in terms of line integrals; for example, the fact that work is equal to force, F, multiplied by displacement, s, may be expressed (in terms of vector quantities) as:^[44]

${\displaystyle W=\mathbf {F} \cdot \mathbf {s} .}$

For an object moving along a path C in a vector field F such as an electric field or gravitational field, the total work done by the field on the object is obtained by summing up the differential work done in moving from s to s + ds. This gives the line integral^[45]

${\displaystyle W=\int _{C}\mathbf {F} \cdot d\mathbf {s} .}$

The definition of surface integral relies on splitting the surface into small surface elements.

A surface integral generalizes double integrals to integration over a surface (which may be a curved set in space); it can be thought of as the double integral analog of the line integral. The function to be integrated may be a scalar field or a vector field. The value of the surface integral is the sum of the field at all points on the surface. This can be achieved by splitting the surface into surface elements, which provide the partitioning for Riemann sums.^[46]

For an example of applications of surface integrals, consider a vector field v on a surface S; that is, for each point x in S, v(x) is a vector. Imagine that a fluid flows through S, such that v(x) determines the velocity of the fluid at x. The flux is defined as the quantity of fluid flowing through S in unit amount of time. To find the flux, one need to take the dot product of v with the unit surface normal to S at each point, which will give a scalar field, which is integrated over the surface:^[47]

${\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }.}$

The fluid flux in this example may be from a physical fluid such as water or air, or from electrical or magnetic flux. Thus surface integrals have applications in physics, particularly with the classical theory of electromagnetism.

Contour integrals

In complex analysis, the integrand is a complex-valued function of a complex variable z instead of a real function of a real variable x. When a complex function is integrated along a curve ${\displaystyle \gamma }$ in the complex plane, the integral is denoted as follows

${\displaystyle \int _{\gamma }f(z)\,dz.}$

This is known as a contour integral.

Integrals of differential forms

A differential form is a mathematical concept in the fields of multivariable calculus, differential topology, and tensors. Differential forms are organized by degree. For example, a one-form is a weighted sum of the differentials of the coordinates, such as:

${\displaystyle E(x,y,z)\,dx+F(x,y,z)\,dy+G(x,y,z)\,dz}$

where E, F, G are functions in three dimensions. A differential one-form can be integrated over an oriented path, and the resulting integral is just another way of writing a line integral. Here the basic differentials dx, dy, dz measure infinitesimal oriented lengths parallel to the three coordinate axes.

A differential two-form is a sum of the form

${\displaystyle G(x,y,z)\,dx\wedge dy+E(x,y,z)\,dy\wedge dz+F(x,y,z)\,dz\wedge dx.}$

Here the basic two-forms ${\displaystyle dx\wedge dy,dz\wedge dx,dy\wedge dz}$ measure oriented areas parallel to the coordinate two-planes. The symbol ${\displaystyle \wedge }$ denotes the wedge product, which is similar to the cross product in the sense that the wedge product of two forms representing oriented lengths represents an oriented area. A two-form can be integrated over an oriented surface, and the resulting integral is equivalent to the surface integral giving the flux of ${\displaystyle E\mathbf {i} +F\mathbf {j} +G\mathbf {k} }$.

Unlike the cross product, and the three-dimensional vector calculus, the wedge product and the calculus of differential forms makes sense in arbitrary dimension and on more general manifolds (curves, surfaces, and their higher-dimensional analogs). The exterior derivative plays the role of the gradient and curl of vector calculus, and Stokes' theorem simultaneously generalizes the three theorems of vector calculus: the divergence theorem, Green's theorem, and the Kelvin-Stokes theorem.

Summations

The discrete equivalent of integration is summation. Summations and integrals can be put on the same foundations using the theory of Lebesgue integrals or time-scale calculus.

Functional integrals

An integration that is performed not over a variable (or, in physics, over a space or time dimension), but over a space of functions, is referred to as a functional integral.

Applications

Integrals are used extensively in many areas. For example, in probability theory, integrals are used to determine the probability of some random variable falling within a certain range.^[48] Moreover, the integral under an entire probability density function must equal 1, which provides a test of whether a function with no negative values could be a density function or not.^[49]

Integrals can be used for computing the area of a two-dimensional region that has a curved boundary, as well as computing the volume of a three-dimensional object that has a curved boundary. The area of a two-dimensional region can be calculated using the aforementioned definite integral.^[50] The volume of a three-dimensional object such as a disc or washer can be computed by disc integration using the equation for the volume of a cylinder, ${\displaystyle \pi r^{2}h}$, where ${\displaystyle r}$ is the radius. In the case of a simple disc created by rotating a curve about the x-axis, the radius is given by f(x), and its height is the differential dx. Using an integral with bounds a and b, the volume of the disc is equal to:^[51] $${\displaystyle \pi \int _{a}^{b}f^{2}(x)\,dx.}$$Integrals are also used in physics, in areas like kinematics to find quantities like displacement, time, and velocity. For example, in rectilinear motion, the displacement of an object over the time interval ${\displaystyle [a,b]}$ is given by

${\displaystyle x(b)-x(a)=\int _{a}^{b}v(t)\,dt,}$

where ${\displaystyle v(t)}$ is the velocity expressed as a function of time.^[52] The work done by a force ${\displaystyle F(x)}$ (given as a function of position) from an initial position ${\displaystyle A}$ to a final position ${\displaystyle B}$ is:^[53]

${\displaystyle W_{A\rightarrow B}=\int _{A}^{B}F(x)\,dx.}$

Integrals are also used in thermodynamics, where thermodynamic integration is used to calculate the difference in free energy between two given states.

Computation

Analytical

The most basic technique for computing definite integrals of one real variable is based on the fundamental theorem of calculus. Let f(x) be the function of x to be integrated over a given interval [a, b]. Then, find an antiderivative of f; that is, a function F such that F′ = f on the interval. Provided the integrand and integral have no singularities on the path of integration, by the fundamental theorem of calculus,

${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}$

Sometimes it is necessary to use one of the many techniques that have been developed to evaluate integrals. Most of these techniques rewrite one integral as a different one which is hopefully more tractable. Techniques include integration by substitution, integration by parts, integration by trigonometric substitution, and integration by partial fractions.

Alternative methods exist to compute more complex integrals. Many nonelementary integrals can be expanded in a Taylor series and integrated term by term. Occasionally, the resulting infinite series can be summed analytically. The method of convolution using Meijer G-functions can also be used, assuming that the integrand can be written as a product of Meijer G-functions. There are also many less common ways of calculating definite integrals; for instance, Parseval's identity can be used to transform an integral over a rectangular region into an infinite sum. Occasionally, an integral can be evaluated by a trick; for an example of this, see Gaussian integral.

Computations of volumes of solids of revolution can usually be done with disk integration or shell integration.

Specific results which have been worked out by various techniques are collected in the list of integrals.

Symbolic

Many problems in mathematics, physics, and engineering involve integration where an explicit formula for the integral is desired. Extensive tables of integrals have been compiled and published over the years for this purpose. With the spread of computers, many professionals, educators, and students have turned to computer algebra systems that are specifically designed to perform difficult or tedious tasks, including integration. Symbolic integration has been one of the motivations for the development of the first such systems, like Macsyma and Maple.

A major mathematical difficulty in symbolic integration is that in many cases, a relatively simple function does not have integrals that can be expressed in closed form involving only elementary functions, include rational and exponential functions, logarithm, trigonometric functions and inverse trigonometric functions, and the operations of multiplication and composition. The Risch algorithm provides a general criterion to determine whether the antiderivative of an elementary function is elementary and to compute the integral if is elementary. However, functions with closed expressions of antiderivatives are the exception, and consequently, computerized algebra systems have no hope of being able to find an antiderivative for a randomly constructed elementary function. On the positive side, if the 'building blocks' for antiderivatives are fixed in advance, it may still be possible to decide whether the antiderivative of a given function can be expressed using these blocks and operations of multiplication and composition and to find the symbolic answer whenever it exists. The Risch algorithm, implemented in Mathematica, Maple and other computer algebra systems, does just that for functions and antiderivatives built from rational functions, radicals, logarithm, and exponential functions.

Some special integrands occur often enough to warrant special study. In particular, it may be useful to have, in the set of antiderivatives, the special functions (like the Legendre functions, the hypergeometric function, the gamma function, the incomplete gamma function and so on). Extending Risch's algorithm to include such functions is possible but challenging and has been an active research subject.

More recently a new approach has emerged, using D-finite functions, which are the solutions of linear differential equations with polynomial coefficients. Most of the elementary and special functions are D-finite, and the integral of a D-finite function is also a D-finite function. This provides an algorithm to express the antiderivative of a D-finite function as the solution of a differential equation. This theory also allows one to compute the definite integral of a D-function as the sum of a series given by the first coefficients and provides an algorithm to compute any coefficient.

Rule-based integration systems facilitate integration. Rubi, a computer algebra system rule-based integrator, pattern matches an extensive system of symbolic integration rules to integrate a wide variety of integrands. This system uses over 6600 integration rules to compute integrals.^[54] The method of brackets is a generalization of Ramanujan's master theorem that can be applied to a wide range of univariate and multivariate integrals. A set of rules are applied to the coefficients and exponential terms of the integrand's power series expansion to determine the integral. The method is closely related to the Mellin transform.^[55]

Numerical

Numerical quadrature methods: rectangle method, trapezoidal rule, Romberg's method, Gaussian quadrature

Definite integrals may be approximated using several methods of numerical integration. The rectangle method relies on dividing the region under the function into a series of rectangles corresponding to function values and multiplies by the step width to find the sum. A better approach, the trapezoidal rule, replaces the rectangles used in a Riemann sum with trapezoids. The trapezoidal rule weights the first and last values by one half, then multiplies by the step width to obtain a better approximation.^[56] The idea behind the trapezoidal rule, that more accurate approximations to the function yield better approximations to the integral, can be carried further: Simpson's rule approximates the integrand by a piecewise quadratic function.^[57]

Riemann sums, the trapezoidal rule, and Simpson's rule are examples of a family of quadrature rules called the Newton–Cotes formulas. The degree n Newton–Cotes quadrature rule approximates the polynomial on each subinterval by a degree n polynomial. This polynomial is chosen to interpolate the values of the function on the interval.^[58] Higher degree Newton–Cotes approximations can be more accurate, but they require more function evaluations, and they can suffer from numerical inaccuracy due to Runge's phenomenon. One solution to this problem is Clenshaw–Curtis quadrature, in which the integrand is approximated by expanding it in terms of Chebyshev polynomials.

Romberg's method halves the step widths incrementally, giving trapezoid approximations denoted by T(h₀), T(h₁), and so on, where h_k+1 is half of h_k. For each new step size, only half the new function values need to be computed; the others carry over from the previous size. It then interpolate a polynomial through the approximations, and extrapolate to T(0). Gaussian quadrature evaluates the function at the roots of a set of orthogonal polynomials.^[59] An n-point Gaussian method is exact for polynomials of degree up to 2n − 1.

The computation of higher-dimensional integrals (for example, volume calculations) makes important use of such alternatives as Monte Carlo integration.^[60]

Mechanical

The area of an arbitrary two-dimensional shape can be determined using a measuring instrument called planimeter. The volume of irregular objects can be measured with precision by the fluid displaced as the object is submerged.

Geometrical

Area can sometimes be found via geometrical compass-and-straightedge constructions of an equivalent square.

Integration by differentiation

Kempf, Jackson and Morales demonstrated mathematical relations that allow an integral to be calculated by means of differentiation. Their calculus involves the Dirac delta function and the partial derivative operator ${\displaystyle \partial _{x}}$. This can also be applied to functional integrals, allowing them to be computed by functional differentiation.^[61]

Examples

Using the fundamental theorem of calculus

The fundamental theorem of calculus allows straightforward calculations of basic functions:

${\displaystyle \int _{0}^{\pi }\sin(x)\,dx=-\cos(x){\big |}_{x=0}^{x=\pi }=-\cos(\pi )-{\big (}-\cos(0){\big )}=2.}$

See also

• Mathematics portal

• Integral equation – Equations with an unknown function under an integral sign
• Integral symbol – Mathematical symbol used to denote integrals and antiderivatives
• Lists of integrals

Notes

1. Integral calculus is a very well established mathematical discipline for which there are many sources. See Apostol 1967 and Anton, Bivens & Davis 2016, for example.

References

1. Burton 2011, p. 117.
2. Heath 2002.
3. Katz 2009, pp. 201–204.
4. Katz 2009, pp. 284–285.
5. Dennis, David; Kreinovich, Vladik; Rump, Siegfried M. (1998-05-01). "Intervals and the Origins of Calculus". Reliable Computing. 4 (2): 191–197. doi:10.1023/A:1009989211143. ISSN 1573-1340.
6. Katz 2009, pp. 305–306.
7. Katz 2009, pp. 516–517.
8. Struik 1986, pp. 215–216.
9. Katz 2009, pp. 536–537.
10. Burton 2011, pp. 385–386.
11. Stillwell 1989, p. 131.
12. Katz 2009, pp. 628–629.
13. Katz 2009, p. 785.
14. Burton 2011, p. 414; Leibniz 1899, p. 154.
15. Cajori 1929, pp. 249–250; Fourier 1822, §231.
16. Cajori 1929, p. 246.
17. Cajori 1929, p. 182.
18. Apostol 1967, p. 74.
19. Anton, Bivens & Davis 2016, p. 259.
20. Apostol 1967, p. 69.
21. Anton, Bivens & Davis 2016, pp. 286−287.
22. Krantz 1991, p. 173.
23. Rudin 1987, p. 5.
24. Siegmund-Schultze 2008, p. 796.
25. Folland 1999, pp. 57–58.
26. Bourbaki 2004, p. IV.43.
27. Lieb & Loss 2001, p. 14.
28. Folland 1999, p. 53.
29. Rudin 1987, p. 25.
30. Apostol 1967, p. 80.
31. Rudin 1987, p. 54.
32. Apostol 1967, p. 81.
33. Rudin 1987, p. 63.
34. Apostol 1967, p. 202.
35. Apostol 1967, p. 205.
36. Montesinos, Zizler & Zizler 2015, p. 355.
37. Apostol 1967, p. 416.
38. Apostol 1967, p. 418.
39. Anton, Bivens & Davis 2016, p. 895.
40. Anton, Bivens & Davis 2016, p. 896.
41. Anton, Bivens & Davis 2016, p. 897.
42. Anton, Bivens & Davis 2016, p. 980.
43. Anton, Bivens & Davis 2016, p. 981.
44. Anton, Bivens & Davis 2016, p. 697.
45. Anton, Bivens & Davis 2016, p. 991.
46. Anton, Bivens & Davis 2016, p. 1014.
47. Anton, Bivens & Davis 2016, p. 1024.
48. Feller 1966, p. 1.
49. Feller 1966, p. 3.
50. Apostol 1967, pp. 88–89.
51. Apostol 1967, pp. 111–114.
52. Anton, Bivens & Davis 2016, p. 306.
53. Apostol 1967, p. 116.
54. Rich, Scheibe & Abbasi 2018.
55. Gonzalez, Jiu & Moll 2020.
56. Dahlquist & Björck 2008, pp. 519–520.
57. Dahlquist & Björck 2008, pp. 522–524.
58. Kahaner, Moler & Nash 1989, p. 144.
59. Kahaner, Moler & Nash 1989, p. 147.
60. Kahaner, Moler & Nash 1989, pp. 139–140.
61. Kempf, Jackson & Morales 2015.

Bibliography

• Anton, Howard; Bivens, Irl C.; Davis, Stephen (2016), Calculus: Early Transcendentals (11th ed.), John Wiley & Sons, ISBN 978-1-118-88382-2
• Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1
• Bourbaki, Nicolas (2004), Integration I, Springer-Verlag, ISBN 3-540-41129-1. In particular chapters III and IV.
• Burton, David M. (2011), The History of Mathematics: An Introduction (7th ed.), McGraw-Hill, ISBN 978-0-07-338315-6
• Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, ISBN 978-0-486-67766-8
• Dahlquist, Germund; Björck, Åke (2008), "Chapter 5: Numerical Integration", Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, archived from the original on 2007-06-15
• Feller, William (1966), An introduction to probability theory and its applications, John Wiley & Sons
• Folland, Gerald B. (1999), Real Analysis: Modern Techniques and Their Applications (2nd ed.), John Wiley & Sons, ISBN 0-471-31716-0
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231
  Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, pp. 200–201
• Gonzalez, Ivan; Jiu, Lin; Moll, Victor H. (1 January 2020), "An extension of the method of brackets. Part 2", Open Mathematics, 18 (1): 983–995, arXiv:1707.08942, doi:10.1515/math-2020-0062, ISSN 2391-5455, S2CID 222004668
• Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4
  (Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H. (1953), "Integration in abstract spaces", Bulletin of the American Mathematical Society, 59 (2): 111–139, doi:10.1090/S0002-9904-1953-09694-X, ISSN 0273-0979
• Kahaner, David; Moler, Cleve; Nash, Stephen (1989), "Chapter 5: Numerical Quadrature", Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8
• Kallio, Bruce Victor (1966), A History of the Definite Integral (PDF) (M.A. thesis), University of British Columbia, archived from the original on 2014-03-05, retrieved 2014-02-28
• Katz, Victor J. (2009), A History of Mathematics: An Introduction, Addison-Wesley, ISBN 978-0-321-38700-4
• Kempf, Achim; Jackson, David M.; Morales, Alejandro H. (2015), "How to (path-)integrate by differentiating", Journal of Physics: Conference Series, 626 (1), IOP Publishing: 012015, arXiv:1507.04348, Bibcode:2015JPhCS.626a2015K, doi:10.1088/1742-6596/626/1/012015, S2CID 119642596
• Krantz, Steven G. (1991), Real Analysis and Foundations, CRC Press, ISBN 0-8493-7156-2
• Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel (ed.), Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller
• Lieb, Elliott; Loss, Michael (2001), Analysis, Graduate Studies in Mathematics, vol. 14 (2nd ed.), American Mathematical Society, ISBN 978-0821827833
• Montesinos, Vicente; Zizler, Peter; Zizler, Václav (2015), An Introduction to Modern Analysis (illustrated ed.), Springer, ISBN 978-3-319-12481-0
• Rich, Albert; Scheibe, Patrick; Abbasi, Nasser (16 December 2018), "Rule-based integration: An extensive system of symbolic integration rules", Journal of Open Source Software, 3 (32): 1073, Bibcode:2018JOSS....3.1073R, doi:10.21105/joss.01073, S2CID 56487062
• Rudin, Walter (1987), "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
• Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover
• Siegmund-Schultze, Reinhard (2008), "Henri Lebesgue", in Timothy Gowers; June Barrow-Green; Imre Leader (eds.), Princeton Companion to Mathematics, Princeton University Press, ISBN 978-0-691-11880-2.
• Stillwell, John (1989), Mathematics and Its History, Springer, ISBN 0-387-96981-0
• Stoer, Josef; Bulirsch, Roland (2002), "Topics in Integration", Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3.
• Struik, Dirk Jan, ed. (1986), A Source Book in Mathematics, 1200-1800, Princeton, New Jersey: Princeton University Press, ISBN 0-691-08404-1
• "Arabic mathematical notation", W3C, 2006

External links

• "Integral", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Online Integral Calculator, Wolfram Alpha.

Online books

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K. D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Johnson, William Woolsey (1909) Elementary Treatise on Integral Calculus, link from HathiTrust.
• Kowalk, W. P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute
• P. S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) — a cookbook of definite integral techniques