fracción continua

Número representado como a0+1/(a1+1/...)

${\displaystyle a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{\ddots +{\cfrac {1}{a_{n}}}}}}}}}}$

Una fracción continua regular finita, donde es un número entero no negativo, es un número entero y es un número entero positivo, para . ${\displaystyle n}$ ${\displaystyle a_{0}}$ ${\displaystyle a_{i}}$ ${\displaystyle i=1,\ldots ,n}$

En matemáticas , una fracción continua es una expresión obtenida mediante un proceso iterativo de representar un número como la suma de su parte entera y el recíproco de otro número, luego escribir este otro número como la suma de su parte entera y otro recíproco, y así en. ^[1] En una fracción continua finita (o fracción continua terminada ), la iteración/ recursión finaliza después de un número finito de pasos utilizando un número entero en lugar de otra fracción continua. En cambio, una fracción continua infinita es una expresión infinita . En cualquier caso, todos los números enteros de la secuencia, excepto el primero, deben ser positivos . Los números enteros se llaman coeficientes o términos de la fracción continua. ^[2] ${\displaystyle a_{i}}$

Generalmente se supone que el numerador de todas las fracciones es 1. Si se usan valores y/o funciones arbitrarias en lugar de uno o más numeradores o números enteros en los denominadores, la expresión resultante es una fracción continua generalizada . Cuando es necesario distinguir la primera forma de las fracciones continuas generalizadas, las primeras pueden denominarse fracción continua simple o regular , o decirse que están en forma canónica .

Las fracciones continuas tienen una serie de propiedades notables relacionadas con el algoritmo euclidiano para números enteros o reales . cada número racional ${\displaystyle p}$/ ${\displaystyle q}$tiene dos expresiones estrechamente relacionadas como fracción continua finita, cuyos coeficientes a _i se pueden determinar aplicando el algoritmo euclidiano a . El valor numérico de una fracción continua infinita es irracional ; se define a partir de su secuencia infinita de números enteros como el límite de una secuencia de valores para fracciones continuas finitas. Cada fracción continua finita de la secuencia se obtiene utilizando un prefijo finito de la secuencia de números enteros que define la fracción continua infinita. Además, cada número irracional es el valor de una fracción continua regular infinita única , cuyos coeficientes se pueden encontrar usando la versión no terminante del algoritmo euclidiano aplicado a los valores inconmensurables y 1. Esta forma de expresar números reales (racionales e irracionales) se llama su representación en fracción continua . ${\displaystyle (p,q)}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha }$

El término fracción continua también puede referirse a representaciones de funciones racionales , que surgen en su teoría analítica . Para este uso del término, véase Aproximación de Padé y Funciones racionales de Chebyshev .

Motivación y notación.

Consideremos, por ejemplo, el número racional 415/93, que ronda el 4,4624. Como primera aproximación , comenzamos con 4, que es la parte entera ;415/93= 4 +43/93. La parte fraccionaria es el recíproco de93/43que es aproximadamente 2,1628. Utilice la parte entera, 2, como aproximación del recíproco para obtener una segunda aproximación de 4 +1/2= 4,5. Ahora,93/43= 2 +7/43; la parte fraccionaria restante,7/43, es el recíproco de43/7, y43/7es alrededor de 6,1429. Utilice 6 como aproximación para obtener 2 +1/6como una aproximación para93/43y 4 +1/2 +1/6, aproximadamente 4,4615, como tercera aproximación. Más,43/7= 6 +1/7. Finalmente, la parte fraccionaria,1/7, es el recíproco de 7, por lo que su aproximación en este esquema, 7, es exacta (7/1= 7 +0/1) y produce la expresión exacta 4 +1/2 +1/6 +1/7para415/93.

La expresión 4 +1/2 +1/6 +1/7se llama representación en fracción continua de415/93. Esto se puede representar mediante la notación abreviada.415/93= [4; 2, 6, 7]. (Es habitual reemplazar solo la primera coma por un punto y coma). Algunos libros de texto más antiguos usan todas las comas en la tupla ( n + 1) , por ejemplo, [4, 2, 6, 7]. ^{[3] [4]}

Si el número inicial es racional, entonces este proceso es exactamente paralelo al algoritmo euclidiano aplicado al numerador y denominador del número. En particular, debe terminar y producir una representación del número en fracción continua finita. La secuencia de números enteros que ocurren en esta representación es la secuencia de cocientes sucesivos calculados por el algoritmo euclidiano. Si el número inicial es irracional , entonces el proceso continúa indefinidamente. Esto produce una secuencia de aproximaciones, todas las cuales son números racionales, y estos convergen al número inicial como límite. Esta es la representación en fracción continua (infinita) del número. Ejemplos de representaciones de fracciones continuas de números irracionales son:

• √ 19 = [4;2,1,3,1,2,8,2,1,3,1,2,8,...] (secuencia A010124 en la OEIS ). El patrón se repite indefinidamente con un período de 6.
• e = [2;1,2,1,1,4,1,1,6,1,1,8,...](secuenciaA003417en elOEIS). El patrón se repite indefinidamente con un período de 3, excepto que se suma 2 a uno de los términos en cada ciclo.
• π = [3;7,15,1,292,1,1,1,2,1,3,1,...] (secuencia A001203 en la OEIS ). Nunca se ha encontrado ningún patrón en esta representación.
• Φ = [1;1,1,1,1,1,1,1,1,1,1,1,...] (secuencia A000012 en el OEIS ). La proporción áurea , el número irracional que es el "más difícil" de aproximar racionalmente (ver § Una propiedad de la proporción áurea φ más abajo) .
• γ = [0;1,1,2,1,2,1,4,3,13,5,1,...] (secuencia A002852 en el OEIS ). La constante de Euler-Mascheroni , que se espera que sea irracional, pero no se sabe, y cuya fracción continua no tiene un patrón aparente.

Las fracciones continuas son, en cierto modo, representaciones más "matemáticamente naturales" de un número real que otras representaciones como las decimales , y tienen varias propiedades deseables:

• La representación en fracción continua de un número real es finita si y sólo si es un número racional. Por el contrario, la representación decimal de un número racional puede ser finita, por ejemplo137/1600= 0,085625 , o infinito con un ciclo repetitivo, por ejemplo4/27= 0,148148148148...
• Cada número racional tiene una representación de fracción continua simple esencialmente única. Cada racional se puede representar exactamente de dos maneras, ya que [ a ₀ ; un ₁ ,... un _{norte −1} , un _norte ] = [ un ₀ ; a ₁ ,... a _{n −1} ,( a _n −1),1] . Por lo general, se elige la primera, más corta, como representación canónica .
• La representación simple de fracción continua de un número irracional es única. (Sin embargo, son posibles representaciones adicionales cuando se utilizan fracciones continuas generalizadas ; ver más abajo).
• Los números reales cuya fracción continua eventualmente se repite son precisamente los irracionales cuadráticos . ^[5] Por ejemplo, la fracción continua repetida [1;1,1,1,...] es la proporción áurea , y la fracción continua repetida [1;2,2,2,...] es la raíz cuadrada de 2 . En cambio, las representaciones decimales de los irracionales cuadráticos son aparentemente aleatorias . Las raíces cuadradas de todos los números enteros (positivos) que no son cuadrados perfectos son irracionales cuadráticos y, por tanto, son fracciones continuas periódicas únicas.
• Las aproximaciones sucesivas generadas al encontrar la representación de fracción continua de un número, es decir, truncando la representación de fracción continua, son en cierto sentido (que se describen a continuación) las "mejores posibles".

Fórmula básica

Una fracción continua ( generalizada ) es una expresión de la forma

${\displaystyle a_{0}+{\cfrac {b_{1}}{a_{1}+{\cfrac {b_{2}}{a_{2}+{\cfrac {b_{3}}{a_{3}+{_{\ddots }}}}}}}}}$

donde a _i y b _i pueden ser números complejos cualesquiera.

Cuando b _i = 1 para todo i, la expresión se llama fracción continua simple . Cuando la expresión contiene un número finito de términos, se llama fracción continua finita . Cuando la expresión contiene infinitos términos, se llama fracción continua infinita . ^[6] Cuando los términos eventualmente se repiten a partir de algún punto en adelante, la expresión se llama fracción continua periódica . ^[5]

Por lo tanto, todo lo siguiente ilustra fracciones continuas simples finitas válidas:

Para fracciones continuas simples de la forma

${\displaystyle r=a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{a_{3}+{_{\ddots }}}}}}}}}$

el término se puede calcular utilizando la siguiente fórmula recursiva: ${\displaystyle a_{n}}$

${\displaystyle a_{n}=\left\lfloor {\frac {N_{n}}{N_{n+1}}}\right\rfloor }$

dónde y ${\displaystyle N_{n+1}=N_{n-1}{\bmod {N}}_{n}}$ ${\displaystyle {\begin{cases}N_{0}=r\\N_{1}=1\end{cases}}}$

De lo cual se puede entender que la secuencia se detiene si . ${\displaystyle a_{n}}$ ${\displaystyle N_{n+1}=0}$

Calcular representaciones de fracciones continuas

Considere un número real . Deja y deja . Cuando , la representación de fracción continua de es , donde está la representación de fracción continua de . Nota: cuando , entonces es la parte entera de y es la parte fraccionaria de . ${\displaystyle r}$ ${\displaystyle i=\lfloor r\rfloor }$ ${\displaystyle f=r-i}$ ${\displaystyle f\neq 0}$ ${\displaystyle r}$ ${\displaystyle [i;a_{1},a_{2},\ldots ]}$ ${\displaystyle [a_{1};a_{2},\ldots ]}$ ${\displaystyle 1/f}$ ${\displaystyle r\geq 0}$ ${\displaystyle i}$ ${\displaystyle r}$ ${\displaystyle f}$ ${\displaystyle r}$

Para calcular una representación de fracción continua de un número , escribe el piso de . Resta este valor de . Si la diferencia es 0, deténgase; de lo contrario encuentre el recíproco de la diferencia y repita. El procedimiento se detendrá si y sólo si es racional. Este proceso se puede implementar de manera eficiente utilizando el algoritmo euclidiano cuando el número es racional. La siguiente tabla muestra una implementación de este procedimiento para el número 3.245, lo que resulta en la expansión de fracción continua . ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle [3;4,12,4]}$

Notaciones

Los números enteros , etc., se denominan coeficientes o términos de la fracción continua. ^[2] Se puede abreviar la fracción continua. ${\displaystyle a_{0}}$ ${\displaystyle a_{1}}$

${\displaystyle x=a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{a_{3}}}}}}}}$

en la notación de Carl Friedrich Gauss

${\displaystyle x=a_{0}+{\underset {i=1}{\overset {3}{\mathrm {K} }}}~{\frac {1}{a_{i}}}}$

o como

${\displaystyle x=[a_{0};a_{1},a_{2},a_{3}]}$,

o en la notación de Pringsheim como

${\displaystyle x=a_{0}+{\frac {1\mid }{\mid a_{1}}}+{\frac {1\mid }{\mid a_{2}}}+{\frac {1\mid }{\mid a_{3}}},}$

o en notaciones relacionadas como

${\displaystyle x=a_{0}+{1 \over a_{1}+{}}{1 \over a_{2}+{}}{1 \over a_{3}{}}}$

o

${\displaystyle x=a_{0}+{1 \over a_{1}}{{} \atop +}{1 \over a_{2}}{{} \atop +}{1 \over a_{3}}.}$

A veces se utilizan corchetes angulares, como este:

${\displaystyle x=\left\langle a_{0};a_{1},a_{2},a_{3}\right\rangle .}$

El punto y coma en las notaciones entre corchetes y corchetes angulares a veces se reemplaza por una coma. ^{[3] [4]}

También se pueden definir infinitas fracciones continuas simples como límites :

${\displaystyle [a_{0};a_{1},a_{2},a_{3},\,\ldots ]=\lim _{n\to \infty }[a_{0};a_{1},a_{2},\,\ldots ,a_{n}].}$

Este límite existe para cualquier elección de números enteros positivos . ^{[7] [8]} ${\displaystyle a_{0}}$ ${\displaystyle a_{1},a_{2},\ldots }$

fracciones continuas finitas

Cada fracción continua finita representa un número racional , y todo número racional se puede representar precisamente de dos maneras diferentes como una fracción continua finita, con las condiciones de que el primer coeficiente sea un número entero y los demás coeficientes sean enteros positivos. Estas dos representaciones concuerdan excepto en sus términos finales. En la representación más larga, el término final de la fracción continua es 1; la representación más corta elimina el 1 final, pero aumenta el nuevo término final en 1. Por lo tanto, el elemento final en la representación corta es siempre mayor que 1, si está presente. En símbolos:

[ un ₀ ; un ₁ , un ₂ , ..., un _{norte − 1} , un _norte , 1] = [ un ₀ ; un ₁ , un ₂ , ..., un _{norte − 1} , un _norte + 1] .

[ un ₀ ; 1] = [ un ₀ + 1] .

Recíprocos

Las representaciones de fracción continua de un número racional positivo y su recíproco son idénticas excepto por un desplazamiento un lugar hacia la izquierda o hacia la derecha dependiendo de si el número es menor o mayor que uno respectivamente. En otras palabras, los números representados por y son recíprocos. ${\displaystyle [a_{0};a_{1},a_{2},\ldots ,a_{n}]}$ ${\displaystyle [0;a_{0},a_{1},\ldots ,a_{n}]}$

Por ejemplo, si es un número entero y luego ${\displaystyle a}$ ${\displaystyle x<1}$

${\displaystyle x=0+{\frac {1}{a+{\frac {1}{b}}}}}$y . ${\displaystyle {\frac {1}{x}}=a+{\frac {1}{b}}}$

Si entonces ${\displaystyle x>1}$

${\displaystyle x=a+{\frac {1}{b}}}$y . ${\displaystyle {\frac {1}{x}}=0+{\frac {1}{a+{\frac {1}{b}}}}}$

El último número que genera el resto de la fracción continua es el mismo para ambos y su recíproco. ${\displaystyle x}$

Por ejemplo,

${\displaystyle 2.25={\frac {9}{4}}=[2;4]}$y . ${\displaystyle {\frac {1}{2.25}}={\frac {4}{9}}=[0;2,4]}$

Infinitas fracciones continuas y convergentes

Convergentes acercándose a la proporción áurea

Toda fracción continua infinita es irracional , y todo número irracional se puede representar precisamente de una manera como una fracción continua infinita.

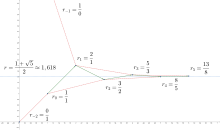
Una representación de fracción continua infinita para un número irracional es útil porque sus segmentos iniciales proporcionan aproximaciones racionales al número. Estos números racionales se llaman convergentes de la fracción continua. ^{[9] [10]} Cuanto mayor es un término en la fracción continua, más cerca está el convergente correspondiente del número irracional que se aproxima. Los números como π ocasionalmente tienen términos grandes en su fracción continua, lo que los hace fáciles de aproximar con números racionales. Otros números como e tienen sólo términos pequeños al principio de su fracción continua, lo que hace que sea más difícil aproximarlos racionalmente. La proporción áurea Φ tiene términos iguales a 1 en todas partes (los valores más pequeños posibles), lo que hace que Φ sea el número más difícil de aproximar racionalmente. En este sentido, por tanto, es el "más irracional" de todos los números irracionales. Los convergentes pares son más pequeños que el número original, mientras que los impares son más grandes.

Para una fracción continua [ a ₀ ; a ₁ , a ₂ , ...] , los primeros cuatro convergentes (numerados del 0 al 3) son

un ₀/1,un ₁ un ₀ + 1/un ₁,un ₂ ( un ₁ un ₀ + 1) + un ₀/un ₂ un ₁ + 1,un ₃ ( un ₂ ( un ₁ un ₀ + 1 ) + un ₀ ) + ( un ₁ un ₀ + 1 )/ un ₃ ( un ₂ un ₁ + 1) + un ₁.

El numerador del tercer convergente se forma multiplicando el numerador del segundo convergente por el tercer coeficiente y sumando el numerador del primer convergente. Los denominadores se forman de manera similar. Por lo tanto, cada convergente puede expresarse explícitamente en términos de la fracción continua como la razón de ciertos polinomios multivariados llamados continuantes .

Si se encuentran convergentes sucesivos, con numeradores h ₁ , h ₂ , ... y denominadores k ₁ , k ₂ , ... entonces la relación recursiva relevante es la de los corchetes gaussianos :

h _norte = un _norte h _{norte - 1} + h _{norte - 2} ,

k _norte = un _norte k _{norte - 1} + k _{norte - 2} .

Los convergentes sucesivos vienen dados por la fórmula

hn _{_}/kn _{_}=una _norte h _{norte - 1} + h _{norte - 2}/una _norte k _{norte - 1} + k _{norte - 2}.

Así, para incorporar un nuevo término a una aproximación racional, sólo son necesarios los dos convergentes anteriores. Los "convergentes" iniciales (requeridos para los dos primeros términos) son ⁰ ⁄ ₁ y ¹ ⁄ ₀ . Por ejemplo, aquí están los convergentes para [0;1,5,2,2].

Cuando se utiliza el método babilónico para generar aproximaciones sucesivas a la raíz cuadrada de un número entero, si se comienza con el número entero más bajo como primera aproximante, todos los racionales generados aparecen en la lista de convergentes para la fracción continua. Específicamente, los aproximantes aparecerán en la lista de convergentes en las posiciones 0, 1, 3, 7, 15, ... ,  2 ^k −1 , ... Por ejemplo, la expansión fraccionaria continua para √ 3 es [1;1, 2,1,2,1,2,1,2,...]. Comparando los convergentes con los aproximantes derivados del método babilónico:

x ₀ = 1 =1/1

x1 = _{_}1/2(1 +3/1) =2/1= 2

x2 = _{_}1/2(2 +3/2) =7/4

x ₃ =1/2(7/4+3/7/4) =97/56

Propiedades

Un espacio de Baire es un espacio topológico sobre infinitas secuencias de números naturales. La fracción continua infinita proporciona un homeomorfismo del espacio de Baire al espacio de números reales irracionales (con la topología subespacial heredada de la topología habitual de los reales). La fracción continua infinita también proporciona una correlación entre los irracionales cuadráticos y los racionales diádicos , y de otros irracionales al conjunto de cadenas infinitas de números binarios (es decir, el conjunto de Cantor ); este mapa se llama función de signo de interrogación de Minkowski . El mapeo tiene interesantes propiedades fractales autosimilares ; estos están dados por el grupo modular , que es el subgrupo de transformaciones de Möbius que tienen valores enteros en la transformación. En términos generales, las fracciones continuas convergentes pueden considerarse transformaciones de Möbius que actúan sobre el semiplano superior (hiperbólico) ; esto es lo que conduce a la autosimetría fractal.

La distribución de probabilidad límite de los coeficientes en la expansión de fracción continua de una variable aleatoria distribuida uniformemente en (0, 1) es la distribución de Gauss-Kuzmin .

Algunos teoremas útiles

Si es una secuencia infinita de números enteros positivos, defina las secuencias y recursivamente: ${\displaystyle \ a_{0}\ ,}$ ${\displaystyle a_{1}\ ,}$ ${\displaystyle a_{2}\ ,}$ ${\displaystyle \ \ldots \ }$ ${\displaystyle \ h_{n}\ }$ ${\displaystyle \ k_{n}\ }$

Teorema 1. Para cualquier número real positivo ${\displaystyle \ x\ }$

${\displaystyle \left[\ a_{0};\ a_{1},\ \dots ,a_{n-1},x\ \right]={\frac {x\ h_{n-1}+h_{n-2}}{\ x\ k_{n-1}+k_{n-2}\ }},\quad \left[\ a_{0};\ a_{1},\ \dots ,a_{n-1}+x\ \right]={\frac {h_{n-1}+xh_{n-2}}{\ k_{n-1}+xk_{n-2}\ }}}$

Teorema 2. Los convergentes de están dados por ${\displaystyle \ [\ a_{0}\ ;}$ ${\displaystyle a_{1}\ ,}$ ${\displaystyle a_{2}\ ,}$ ${\displaystyle \ldots \ ]\ }$

${\displaystyle \left[\ a_{0};\ a_{1},\ \dots ,a_{n}\ \right]={\frac {h_{n}}{\ k_{n}\ }}~.}$

o en forma matricial,

$${\displaystyle {\begin{bmatrix}h_{n}&h_{n-1}\\k_{n}&k_{n-1}\end{bmatrix}}={\begin{bmatrix}a_{0}&1\\1&0\end{bmatrix}}\cdots {\begin{bmatrix}a_{n}&1\\1&0\end{bmatrix}}}$$

Teorema 3. Si la ésima convergente a una fracción continua es entonces ${\displaystyle \ n}$ ${\displaystyle \ {\frac {h_{n}}{k_{n}}}\ ,}$

${\displaystyle k_{n}\ h_{n-1}-k_{n-1}\ h_{n}=(-1)^{n}\ ,}$

o equivalente

${\displaystyle {\frac {h_{n}}{\ k_{n}\ }}-{\frac {h_{n-1}}{\ k_{n-1}\ }}={\frac {(-1)^{n+1}}{\ k_{n-1}\ k_{n}\ }}~.}$

Corolario 1: Cada convergente está en sus términos más bajos (porque si y tuviera un divisor común no trivial se dividiría, lo cual es imposible). ${\displaystyle \ h_{n}\ }$ ${\displaystyle \ k_{n}\ }$ ${\displaystyle \ k_{n}\ h_{n-1}-k_{n-1}\ h_{n}\ ,}$

Corolario 2: La diferencia entre convergentes sucesivos es una fracción cuyo numerador es la unidad:

${\displaystyle {\frac {h_{n}}{k_{n}}}-{\frac {h_{n-1}}{k_{n-1}}}={\frac {\ h_{n}\ k_{n-1}-k_{n}\ h_{n-1}\ }{\ k_{n}\ k_{n-1}\ }}={\frac {(-1)^{n+1}}{\ k_{n}\ k_{n-1}\ }}~.}$

Corolario 3: La fracción continua equivale a una serie de términos alternos:

${\displaystyle a_{0}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{\ k_{n}\ k_{n+1}\ }}~.}$

Corolario 4: La matriz

${\displaystyle {\begin{bmatrix}h_{n}&h_{n-1}\\k_{n}&k_{n-1}\end{bmatrix}}={\begin{bmatrix}a_{0}&1\\1&0\end{bmatrix}}\cdots {\begin{bmatrix}a_{n}&1\\1&0\end{bmatrix}}}$

tiene determinante y, por tanto, pertenece al grupo de matrices unimodulares ${\displaystyle (-1)^{n+1}}$ ${\displaystyle \ 2\times 2\ }$ ${\displaystyle \ \mathrm {GL} (2,\mathbb {Z} )~.}$

Corolario 5: La matriz

$${\displaystyle {\begin{bmatrix}h_{n}&h_{n-2}\\k_{n}&k_{n-2}\end{bmatrix}}={\begin{bmatrix}h_{n}&h_{n-1}\\k_{n}&k_{n-1}\end{bmatrix}}{\begin{bmatrix}a_{n}&0\\1&1\end{bmatrix}}}$$

${\displaystyle (-1)^{n}a_{n}}$

$${\displaystyle {\frac {h_{n}}{\ k_{n}\ }}-{\frac {h_{n-2}}{\ k_{n-2}\ }}={\frac {(-1)^{n}}{\ k_{n-2}\ k_{n}\ }}a_{n}}$$

Corolario 6: La secuencia del denominador satisface la relación de recurrencia y crece al menos tan rápido como la secuencia de Fibonacci , que a su vez crece como donde está la proporción áurea . ${\displaystyle k_{0},k_{1},k_{2},\dots }$ ${\displaystyle k_{-1}=0,k_{0}=1,k_{n}=k_{n-1}a_{n}+k_{n-2}}$ ${\displaystyle O(\phi ^{n})}$ ${\displaystyle \phi =1.618\dots }$

Teorema 4. Cada ( ésimo) convergente está más cerca de un ( ésimo) convergente posterior que cualquier convergente ( ésimo) anterior. En símbolos, si se considera que el ésimo convergente es entonces ${\displaystyle \ s}$ ${\displaystyle \ n}$ ${\displaystyle \ r}$ ${\displaystyle \ n}$ ${\displaystyle \ \left[\ a_{0};\ a_{1},\ \ldots ,\ a_{n}\ \right]=x_{n}\ ,}$

${\displaystyle \left|\ x_{r}-x_{n}\ \right|>\left|\ x_{s}-x_{n}\ \right|}$

para todos ${\displaystyle \ r<s<n~.}$

Corolario 1: Los convergentes pares (antes del ésimo) aumentan continuamente, pero siempre son menores que ${\displaystyle \ n}$ ${\displaystyle \ x_{n}~.}$

Corolario 2: Los convergentes impares (antes del ésimo) disminuyen continuamente, pero siempre son mayores que ${\displaystyle \ n}$ ${\displaystyle \ x_{n}~.}$

Teorema 5.

${\displaystyle {\frac {1}{\ k_{n}\ (k_{n+1}+k_{n})\ }}<\left|\ x-{\frac {h_{n}}{\ k_{n}\ }}\ \right|<{\frac {1}{\ k_{n}\ k_{n+1}\ }}~.}$

Corolario 1: Un convergente está más cerca del límite de la fracción continua que cualquier fracción cuyo denominador sea menor que el del convergente.

Corolario 2: Un convergente obtenido al terminar la fracción continua justo antes de un término grande es una aproximación cercana al límite de la fracción continua.

Teorema 6: Considere el conjunto de todos los intervalos abiertos con puntos finales . Denotalo como . Cualquier subconjunto abierto de es una unión disjunta de conjuntos de . ${\displaystyle [0;a_{1},\dots ,a_{n}],[0;a_{1},\dots ,a_{n}+1]}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle [0,1]\setminus \mathbb {Q} }$ ${\displaystyle {\mathcal {C}}}$

Corolario: La fracción continua infinita proporciona un homeomorfismo desde el espacio de Baire hasta . ${\displaystyle [0,1]\setminus \mathbb {Q} }$

Semiconvergentes

Si

${\displaystyle {\frac {h_{n-1}}{k_{n-1}}},{\frac {h_{n}}{k_{n}}}}$

son convergentes consecutivos, entonces cualquier fracción de la forma

${\displaystyle {\frac {h_{n-1}+mh_{n}}{k_{n-1}+mk_{n}}},}$

donde es un número entero tal que , se llaman semiconvergentes , convergentes secundarios o fracciones intermedias . El -st semiconvergente es igual al mediante del -ésimo y el convergente . A veces se entiende que el término significa que ser semiconvergente excluye la posibilidad de ser convergente (es decir, ), en lugar de que un convergente sea un tipo de semiconvergente. ${\displaystyle m}$ ${\displaystyle 0\leq m\leq a_{n+1}}$ ${\displaystyle (m+1)}$ ${\displaystyle m}$ ${\displaystyle {\tfrac {h_{n}}{k_{n}}}}$ ${\displaystyle 0<m<a_{n+1}}$

De ello se deduce que los semiconvergentes representan una secuencia monótona de fracciones entre los convergentes (correspondiente a ) y (correspondiente a ). Los semiconvergentes consecutivos y satisfacen la propiedad . ${\displaystyle {\tfrac {h_{n-1}}{k_{n-1}}}}$ ${\displaystyle m=0}$ ${\displaystyle {\tfrac {h_{n+1}}{k_{n+1}}}}$ ${\displaystyle m=a_{n+1}}$ ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle {\tfrac {c}{d}}}$ ${\displaystyle ad-bc=\pm 1}$

Si una aproximación racional a un número real es tal que el valor es menor que el de cualquier aproximación con un denominador menor, entonces es semiconvergente de la expansión fraccionaria continua de . Sin embargo, lo contrario no es cierto. ${\displaystyle {\tfrac {p}{q}}}$ ${\displaystyle x}$ ${\displaystyle \left|x-{\tfrac {p}{q}}\right|}$ ${\displaystyle {\tfrac {p}{q}}}$ ${\displaystyle x}$

Mejores aproximaciones racionales

Se puede optar por definir la mejor aproximación racional a un número real x como un número racionalnorte/d, d > 0 , que está más cerca de x que cualquier aproximación con un denominador igual o menor. La fracción continua simple para x se puede utilizar para generar todas las mejores aproximaciones racionales para x aplicando estas tres reglas:

1. Trunca la fracción continua y reduce su último término en una cantidad elegida (posiblemente cero).
2. El plazo reducido no podrá tener menos de la mitad de su valor original.
3. Si el término final es par, la mitad de su valor es admisible sólo si el semiconvergente correspondiente es mejor que el convergente anterior. (Vea abajo.)

Por ejemplo, 0,84375 tiene fracción continua [0;1,5,2,2]. Aquí están todas sus mejores aproximaciones racionales.

Mejores aproximantes racionales para π (círculo verde), e (diamante azul), ϕ (oblongo rosa), (√3)/2 (hexágono gris), 1/√2 (octógono rojo) y 1/√3 (triángulo naranja) calculado a partir de sus expansiones de fracciones continuas, representadas como pendientes y / x con errores de sus valores verdaderos (guiones negros)  

• v
• t
• mi

El aumento estrictamente monótono de los denominadores a medida que se incluyen términos adicionales permite que un algoritmo imponga un límite, ya sea en el tamaño del denominador o en la cercanía de la aproximación.

La "regla de la mitad" mencionada anteriormente requiere que cuando a _k es par, el término reducido a la mitad a _k /2 es admisible si y sólo si | x − [ a ₀  ; un ₁ , ..., un _{k − 1} ]| > | x − [ a ₀  ; un ₁ , ..., un _{k − 1} , un _k /2]| ^[11] Esto es equivalente ^[11] a: Shoemake (1995).

[ a _k ; un _{k − 1} , ..., un ₁ ] > [ un _k ; a _{k + 1} , ...] .

Los convergentes a x son "mejores aproximaciones" en un sentido mucho más fuerte que el definido anteriormente. Es decir, n / d es convergente para x si y sólo si | dx − norte | tiene el valor más pequeño entre las expresiones análogas para todas las aproximaciones racionales m / c con c ≤ d ; es decir, tenemos | dx − norte | < | cx - m | siempre que c < d . (Tenga en cuenta también que | d _k x − n _k | → 0 como k → ∞ .)

Mejor racional dentro de un intervalo

Un racional que cae dentro del intervalo ( x ,  y ) , para 0 < x < y , se puede encontrar con las fracciones continuas para x e y . Cuando tanto x como y son irracionales y

x = [ a ₀ ; un ₁ , un ₂ , ..., un _{k - 1} , un _k , un _{k + 1} , ...]

y = [ a ₀ ; un ₁ , un ₂ , ..., un _{k - 1} , segundo _k , segundo _{k + 1} , ...]

donde x e y tienen expansiones de fracciones continuas idénticas hasta k ₋₁ , un racional que cae dentro del intervalo ₍ x , y  ) está dado por la fracción continua finita,

z ( x , y ) = [ a ₀ ; a ₁ , a ₂ , ..., a _{k − 1} , min( a _k , b _k ) + 1]

Este racional será mejor en el sentido de que ningún otro racional en ( x ,  y ) tendrá un numerador o un denominador más pequeño. ^{[ cita necesaria ]}

Si x es racional, tendrá dos representaciones de fracciones continuas que son finitas , x ₁ y x ₂ , y de manera similar una  y racional tendrá dos representaciones, y ₁ e y ₂ . Los coeficientes posteriores al último en cualquiera de estas representaciones deben interpretarse como +∞ ; y el mejor racional será uno de z ( x ₁ ,  y ₁ ) , z ( x ₁ ,  y ₂ ) , z ( x ₂ ,  y ₁ ) , o z ( x ₂ ,  y ₂ ) .

Por ejemplo, la representación decimal 3,1416 podría redondearse desde cualquier número en el intervalo [3,14155, 3,14165) . Las representaciones de fracción continua de 3,14155 y 3,14165 son

3,14155 = [3; 7, 15, 2, 7, 1, 4, 1, 1] = [3; 7, 15, 2, 7, 1, 4, 2]

3,14165 = [3; 7, 16, 1, 3, 4, 2, 3, 1] = [3; 7, 16, 1, 3, 4, 2, 4]

y el mejor racional entre estos dos es

[3; 7, 16] =355/113= 3,1415929....

De este modo,355/113es el mejor número racional correspondiente al número decimal redondeado 3,1416, en el sentido de que ningún otro número racional que se redondearía a 3,1416 tendrá un numerador o un denominador más pequeño.

Intervalo para un convergente

Un número racional, que se puede expresar como fracción continua finita de dos maneras,

z = [ a ₀ ; un ₁ , ..., un _{k - 1} , un _k , 1] = [ un ₀ ; un ₁ , ..., un _{k − 1} , un _k + 1] =paquete _{_}/q _k

será uno de los convergentes para la expansión fraccionaria continua de un número, si y sólo si el número está estrictamente entre (ver esta prueba)

x = [ a ₀ ; un ₁ , ..., un _{k − 1} , un _k , 2] =2 p _k - p _k-1/2 q _k - q _k-1y

y = [ a ₀ ; un ₁ , ..., un _{k − 1} , un _k + 2] =pk ₊ pk _- 1/q _k + q _k-1

Los números x e y se forman incrementando el último coeficiente en las dos representaciones de z . Se da el caso de que x < y cuando k es par y x > y cuando k es impar.

Por ejemplo, el número355/113tiene las representaciones de fracciones continuas

355/113= [3; 7, 15, 1] ​​= [3; 7, 16]

y por lo tanto355/113es convergente de cualquier número estrictamente entre

Comparación

Considere x = [ a ₀ ; a ₁ , ...] y y = [ b ₀ ; b ₁ , ...] . Si k es el índice más pequeño para el cual a _k es desigual a b _k entonces x < y si (−1) ^k ( a _k − b _k ) < 0 e y < x en caso contrario.

Si no existe tal k , pero una expansión es más corta que la otra, digamos x = [ a ₀ ; a ₁ , ..., _an ] e y = [ b ₀ ; b ₁ , ..., b _n , b _{n + 1} , ...] con a _i = b _i para 0 ≤ i ≤ n , entonces x < y si n es par e y < x si n es impar.

Expansión fraccionaria continua de π y sus convergentes

Para calcular los convergentes de π podemos establecer a ₀ = ⌊ π ⌋ = 3 , definir u ₁ =1/π -3≈ 7.0625 y a ₁ = ⌊ u ₁ ⌋ = 7 , u ₂ =1/tu ₁ − 7≈ 15.9966 y a ₂ = ⌊ u ₂ ⌋ = 15 , u ₃ =1/tu ₂ − 15≈ 1,0034 . Continuando así, se puede determinar la fracción continua infinita de π como

[3;7,15,1,292,1,1,...] (secuencia A001203 en el OEIS ).

El cuarto convergente de π es [3;7,15,1] =355/113= 3,14159292035..., a veces llamado Milü , que está bastante cerca del valor real de π .

Supongamos que los cocientes encontrados son, como arriba, [3;7,15,1]. La siguiente es una regla mediante la cual podemos escribir de una vez las fracciones convergentes que resultan de estos cocientes sin desarrollar la fracción continua.

El primer cociente, supuesto dividido por la unidad, dará la primera fracción, que será demasiado pequeña, es decir,3/1. Luego, multiplicando el numerador y denominador de esta fracción por el segundo cociente y sumando la unidad al numerador, tendremos la segunda fracción,22/7, que será demasiado grande. Multiplicando de igual manera el numerador y denominador de esta fracción por el tercer cociente, y sumando al numerador el numerador de la fracción anterior, y al denominador el denominador de la fracción anterior, tendremos la tercera fracción, que será también pequeño. Así, siendo el tercer cociente 15, tenemos como numerador (22 × 15 = 330) + 3 = 333 , y como denominador, (7 × 15 = 105) + 1 = 106 . El tercer convergente, por tanto, es333/106. Procedemos de la misma manera para el cuarto convergente. Siendo el cuarto cociente 1, decimos 333 por 1 es 333, y éste más 22, el numerador de la fracción anterior, es 355; de manera similar, 106 por 1 es 106, y este más 7 es 113. De esta manera, empleando los cuatro cocientes [3;7,15,1], obtenemos las cuatro fracciones:

3/1,22/7,333/106,355/113, ....

El siguiente código Maple generará expansiones fraccionarias continuas de pi

En resumen, el patrón es ${\displaystyle {\text{Numerator}}_{i}={\text{Numerator}}_{(i-1)}\cdot {\text{Quotient}}_{i}+{\text{Numerator}}_{(i-2)}}$ ${\displaystyle {\text{Denominator}}_{i}={\text{Denominator}}_{(i-1)}\cdot {\text{Quotient}}_{i}+{\text{Denominator}}_{(i-2)}}$

Estos convergentes son alternativamente más pequeños y más grandes que el valor verdadero de π , y se acercan cada vez más a π . La diferencia entre un convergente dado y π es menor que el recíproco del producto de los denominadores de ese convergente y el siguiente convergente. Por ejemplo, la fracción22/7es mayor que π , pero22/7− π es menor que1/7 × 106 = 1/742(En realidad,22/7− π es un poco más que1/791=1/7 × 113).

La demostración de las propiedades anteriores se deduce de que si buscamos la diferencia entre una de las fracciones convergentes y la siguiente adyacente a ella obtendremos una fracción cuyo numerador es siempre la unidad y el denominador el producto de los dos denominadores. . Así la diferencia entre22/7y3/1es1/7, en exceso; entre333/106y22/7,1/742, en déficit; entre355/113y333/106,1/11978, en exceso; etcétera. El resultado es que empleando esta serie de diferencias podemos expresar de otra manera muy sencilla las fracciones que aquí nos ocupan, por medio de una segunda serie de fracciones cuyos numeradores son todos la unidad y los denominadores son sucesivamente los producto de cada dos denominadores adyacentes. En lugar de las fracciones escritas arriba, tenemos así la serie:

3/1+1/1 × 7−1/7 × 106+1/106 × 113−...

El primer término, como vemos, es la primera fracción; el primero y el segundo juntos dan la segunda fracción,22/7; el primero, el segundo y el tercero dan la tercera fracción333/106, y así sucesivamente con el resto; el resultado es que toda la serie es equivalente al valor original.

Fracción continua generalizada

Una fracción continua generalizada es una expresión de la forma

${\displaystyle x=b_{0}+{\cfrac {a_{1}}{b_{1}+{\cfrac {a_{2}}{b_{2}+{\cfrac {a_{3}}{b_{3}+{\cfrac {a_{4}}{b_{4}+\ddots \,}}}}}}}}}$

donde a _n ( n > 0) son los numeradores parciales, b _n son los denominadores parciales y el término principal b ₀ se llama parte entera de la fracción continua.

Para ilustrar el uso de fracciones continuas generalizadas, considere el siguiente ejemplo. La secuencia de denominadores parciales de la fracción continua simple de π no muestra ningún patrón obvio:

${\displaystyle \pi =[3;7,15,1,292,1,1,1,2,1,3,1,\ldots ]}$

o

${\displaystyle \pi =3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+{\cfrac {1}{292+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{3+{\cfrac {1}{1+\ddots }}}}}}}}}}}}}}}}}}}}}}}$

Sin embargo, varias fracciones continuas generalizadas para π tienen una estructura perfectamente regular, como por ejemplo:

${\displaystyle \pi ={\cfrac {4}{1+{\cfrac {1^{2}}{2+{\cfrac {3^{2}}{2+{\cfrac {5^{2}}{2+{\cfrac {7^{2}}{2+{\cfrac {9^{2}}{2+\ddots }}}}}}}}}}}}={\cfrac {4}{1+{\cfrac {1^{2}}{3+{\cfrac {2^{2}}{5+{\cfrac {3^{2}}{7+{\cfrac {4^{2}}{9+\ddots }}}}}}}}}}=3+{\cfrac {1^{2}}{6+{\cfrac {3^{2}}{6+{\cfrac {5^{2}}{6+{\cfrac {7^{2}}{6+{\cfrac {9^{2}}{6+\ddots }}}}}}}}}}}$

${\displaystyle \displaystyle \pi =2+{\cfrac {2}{1+{\cfrac {1}{1/2+{\cfrac {1}{1/3+{\cfrac {1}{1/4+\ddots }}}}}}}}=2+{\cfrac {2}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}}$

${\displaystyle \displaystyle \pi =2+{\cfrac {4}{3+{\cfrac {1\cdot 3}{4+{\cfrac {3\cdot 5}{4+{\cfrac {5\cdot 7}{4+\ddots }}}}}}}}}$

Los dos primeros son casos especiales de la función arcotangente con π = 4 arctan (1) y el cuarto y quinto se pueden derivar usando el producto de Wallis . ^{[12] [13]}

${\displaystyle \pi =3+{\cfrac {1}{6+{\cfrac {1^{3}+2^{3}}{6\cdot 1^{2}+1^{2}{\cfrac {1^{3}+2^{3}+3^{3}+4^{3}}{6\cdot 2^{2}+2^{2}{\cfrac {1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}}{6\cdot 3^{2}+3^{2}{\cfrac {1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}+7^{3}+8^{3}}{6\cdot 4^{2}+\ddots }}}}}}}}}}}$

La fracción continua de arriba que consta de cubos utiliza la serie Nilakantha y una hazaña de Leonhard Euler. ^[14] ${\displaystyle \pi }$

Otras expansiones de fracciones continuas

fracciones periódicas continuas

Los números con expansión periódica de fracción continua son precisamente las soluciones irracionales de ecuaciones cuadráticas con coeficientes racionales; Las soluciones racionales tienen expansiones de fracciones continuas finitas como se indicó anteriormente. Los ejemplos más simples son la proporción áurea φ = [1;1,1,1,1,1,...] y √ 2 = [1;2,2,2,2,...], mientras que √ 14 = [3;1,2,1,6,1,2,1,6...] y √ 42 = [6;2,12,2,12,2,12...]. Todas las raíces cuadradas irracionales de números enteros tienen una forma especial para el período; una cadena simétrica, como la cadena vacía (para √ 2 ) o 1,2,1 (para √ 14 ), seguida del doble del entero principal.

Una propiedad de la proporción áurea φ

Debido a que la expansión fraccional continua para φ no utiliza ningún número entero mayor que 1, φ es uno de los números reales más "difíciles" de aproximar con números racionales. El teorema de Hurwitz ^[15] establece que cualquier número irracional k puede aproximarse mediante infinitos números racionales.metro/nortecon

${\displaystyle \left|k-{m \over n}\right|<{1 \over n^{2}{\sqrt {5}}}.}$

Si bien prácticamente todos los números reales k eventualmente tendrán infinitos convergentesmetro/nortecuya distancia de k es significativamente menor que este límite, los convergentes para φ (es decir, los números5/3,8/5,13/8,21/13, etc.) consistentemente "siguen el límite", manteniendo una distancia casi exacta de φ, por lo que nunca producen una aproximación tan impresionante como, por ejemplo, ${\displaystyle {\scriptstyle {1 \over n^{2}{\sqrt {5}}}}}$355/113para π . También se puede demostrar que todo número real de la formaa + b φ/c + re φ, donde a , b , c y d son números enteros tales que a  d − b  c = ±1 , comparte esta propiedad con la proporción áurea φ; y que todos los demás números reales pueden aproximarse más estrechamente.

Patrones regulares en fracciones continuas.

Si bien no hay un patrón discernible en la expansión de fracción continua simple de π , hay uno para e , la base del logaritmo natural :

${\displaystyle e=e^{1}=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,\dots ],}$

que es un caso especial de esta expresión general para entero positivo n :

${\displaystyle e^{1/n}=[1;n-1,1,1,3n-1,1,1,5n-1,1,1,7n-1,1,1,\dots ]\,\!.}$

Otro patrón más complejo aparece en esta expansión de fracción continua para n impar positivo :

${\displaystyle e^{2/n}=\left[1;{\frac {n-1}{2}},6n,{\frac {5n-1}{2}},1,1,{\frac {7n-1}{2}},18n,{\frac {11n-1}{2}},1,1,{\frac {13n-1}{2}},30n,{\frac {17n-1}{2}},1,1,\dots \right]\,\!,}$

con un caso especial para n = 1 :

${\displaystyle e^{2}=[7;2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,11,1,1,12,54,14,1,1\dots ,3k,12k+6,3k+2,1,1\dots ]\,\!.}$

Otras fracciones continuas de este tipo son

${\displaystyle \tanh(1/n)=[0;n,3n,5n,7n,9n,11n,13n,15n,17n,19n,\dots ]}$

donde n es un número entero positivo; además, para el número entero n :

${\displaystyle \tan(1/n)=[0;n-1,1,3n-2,1,5n-2,1,7n-2,1,9n-2,1,\dots ]\,\!,}$

con un caso especial para n = 1 :

${\displaystyle \tan(1)=[1;1,1,3,1,5,1,7,1,9,1,11,1,13,1,15,1,17,1,19,1,\dots ]\,\!.}$

Si In ( x ) es la _función de Bessel modificada o hiperbólica del primer tipo, podemos definir una función sobre los racionalespag/qpor

${\displaystyle S(p/q)={\frac {I_{p/q}(2/q)}{I_{1+p/q}(2/q)}},}$

que se define para todos los números racionales, con p y q en sus términos más bajos. Entonces, para todos los racionales no negativos, tenemos

${\displaystyle S(p/q)=[p+q;p+2q,p+3q,p+4q,\dots ],}$

con fórmulas similares para racionales negativos; en particular tenemos

${\displaystyle S(0)=S(0/1)=[1;2,3,4,5,6,7,\dots ].}$

Muchas de las fórmulas se pueden demostrar utilizando la fracción continua de Gauss .

Fracciones continuas típicas

La mayoría de los números irracionales no tienen ningún comportamiento periódico o regular en su expansión fraccionaria continua. Sin embargo, para casi todos los números del intervalo unitario tienen el mismo comportamiento límite.

La media aritmética diverge: , por lo que los coeficientes crecen arbitrariamente: . En particular, esto implica que casi todos los números son bien aproximables, en el sentido de que ${\displaystyle \lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n}a_{k}=+\infty }$ ${\displaystyle \limsup _{n}a_{n}=+\infty }$

$${\displaystyle \liminf _{n\to \infty }\left|x-{\frac {p_{n}}{q_{n}}}\right|q_{n}^{2}=0}$$

Khinchinmedia geométricaa _iconstante de Khinchin

$${\displaystyle \lim _{n\rightarrow \infty }\left(a_{1}a_{2}...a_{n}\right)^{1/n}=K_{0}=2.6854520010\dots }$$

Paul Lévyn-nconstante de Lévy

$${\displaystyle \lim _{n\rightarrow \infty }q_{n}^{1/n}=e^{\pi ^{2}/(12\ln 2)}=3.2758\ldots }$$

El teorema de Lochs

$${\displaystyle \lim _{n\to \infty }{\frac {1}{n}}\ln \left|x-{\frac {p_{n}}{q_{n}}}\right|=-{\frac {\pi ^{2}}{6\ln 2}}}$$

Aplicaciones

Raíces cuadradas

Las fracciones continuas generalizadas se utilizan en un método para calcular raíces cuadradas .

La identidad

conduce mediante recursividad a la fracción continua generalizada para cualquier raíz cuadrada: ^[16]

ecuación de pell

Las fracciones continuas juegan un papel esencial en la solución de la ecuación de Pell . Por ejemplo, para enteros positivos p y q , y n no cuadrados , es cierto que si p ² − nq ² = ±1 , entoncespag/qes convergente de la fracción continua regular para √ n . Lo contrario se cumple si el período de la fracción continua regular para √ n es 1 y, en general, el período describe qué convergentes dan soluciones a la ecuación de Pell. ^[17]

Sistemas dinámicos

Las fracciones continuas también desempeñan un papel en el estudio de los sistemas dinámicos , donde unen las fracciones de Farey que se ven en el conjunto de Mandelbrot con la función del signo de interrogación de Minkowski y el grupo modular Gamma.

El operador de desplazamiento hacia atrás para fracciones continuas es el mapa h ( x ) = 1/ x − ⌊1/ x ⌋ llamado mapa de Gauss , que corta dígitos de una expansión de fracción continua: h ([0; a ₁ , a ₂ , a ₃ , ...]) = [0; un ₂ , un ₃ ,...] . El operador de transferencia de este mapa se llama operador Gauss-Kuzmin-Wirsing . La distribución de los dígitos en fracciones continuas viene dada por el vector propio cero de este operador, y se denomina distribución de Gauss-Kuzmin .

Valores propios y vectores propios

El algoritmo de Lanczos utiliza una expansión de fracción continua para aproximar iterativamente los valores propios y los vectores propios de una matriz dispersa grande. ^[18]

Aplicaciones de red

Las fracciones continuas también se han utilizado en el modelado de problemas de optimización para la virtualización de redes inalámbricas para encontrar una ruta entre un origen y un destino. ^[19]

Ejemplos de números racionales e irracionales

ra : aproximante racional obtenida expandiendo la fracción continua hasta a _r

Historia

• 300 a. C. Los Elementos de Euclides contiene un algoritmo para el máximo común divisor , cuya versión moderna genera una fracción continua como la secuencia de cocientes de las sucesivas divisiones euclidianas que se producen en ella.
• 499 El Aryabhatiya contiene la solución de ecuaciones indeterminadas usando fracciones continuas.
• 1572 Rafael Bombelli , L'Algebra Opera - método para la extracción de raíces cuadradas que se relaciona con fracciones continuas
• 1613 Pietro Cataldi , Trattato del modo brevissimo di trovar la radice quadra delli numeri - primera notación para fracciones continuas

Cataldi representó una fracción continua como & & & con los puntos indicando dónde iban las siguientes fracciones. ${\displaystyle a_{0}}$ ${\displaystyle {\frac {n_{1}}{d_{1}\cdot }}}$ ${\displaystyle {\frac {n_{2}}{d_{2}\cdot }}}$ ${\displaystyle {\frac {n_{3}}{d_{3}\cdot }}}$

• 1695 John Wallis , Opera Mathematica - introducción del término "fracción continua"
• 1737 Leonhard Euler , De fraccionibus continuis dissertatio : proporcionó la primera explicación entonces completa de las propiedades de las fracciones continuas e incluyó la primera prueba de que el número e es irracional. ^[20]
• 1748 Euler, Introductio in analysin infinitorum . vol. I, Capítulo 18 – probé la equivalencia de una cierta forma de fracción continua y una serie infinita generalizada , probé que todo número racional puede escribirse como una fracción continua finita y probé que la fracción continua de un número irracional es infinita. ^[21]
• 1761 Johann Lambert : dio la primera prueba de la irracionalidad de π utilizando una fracción continua para tan(x) .
• 1768 Joseph-Louis Lagrange : proporcionó la solución general a la ecuación de Pell utilizando fracciones continuas similares a la de Bombelli.
• 1770 Lagrange: demostró que los irracionales cuadráticos se expanden a fracciones continuas periódicas .
• 1813 Carl Friedrich Gauss , Obra , vol. 3, págs. 134-138: derivó una fracción continua de valores complejos muy general a través de una identidad inteligente que involucra la función hipergeométrica
• 1892 Henri Padé definió Padé aproximante
• 1972 Bill Gosper : primeros algoritmos exactos para aritmética de fracciones continuas.

Ver también

• paréntesis gaussianos
• Fracción continua generalizada  : generalización de fracciones continuas en las que los numeradores parciales y los denominadores parciales pueden asumir valores complejos arbitrarios.Pages displaying wikidata descriptions as a fallback
• fracción continua periódica
• Logaritmos continuos
• cociente completo
• Calcular fracciones continuas de raíces cuadradas  – Algoritmos para calcular raíces cuadradas
• Fracción egipcia  : suma finita de fracciones unitarias distintas
• Expansión de Engel  : descomposición de un número real positivo en una serie de fracciones unitarias, cada una de las cuales es un múltiplo entero de la siguientePages displaying wikidata descriptions as a fallback
• Fórmula de fracción continua de Euler  : conecta una serie infinita muy general con una fracción continua infinita.
• Composiciones infinitas de funciones analíticas  : teoría matemática sobre la composición de funciones infinitamente iteradas
• Producto infinito  – Concepto matemático
• Operación binaria iterada  : aplicación repetida de una operación a una secuencia
• Poliedro de Klein  – Concepto en la geometría de los números
• Constantes matemáticas por representación de fracción continua
• Cocientes parciales restringidos
• Árbol de Stern-Brocot  : árbol binario ordenado de números racionales
• Teorema de Śleszyński-Pringsheim  : criterio de convergencia de fracciones continuas

Notas

1. Enciclopedia Británica 2013.
2. Pettofrezzo y Byrkit 1970, pág. 150.
3. Long 1972, pág. 173.
4. Pettofrezzo y Byrkit 1970, pág. 152.
5. Weisstein 2022.
6. Collins 2001.
7. Largo 1972, pag. 183.
8. Pettofrezzo y Byrkit 1970, pág. 158.
9. Largo 1972, pag. 177.
10. Pettofrezzo y Byrkit 1970, págs. 162-163.
11. Thill 2008.
12. Bunder y Tonien 2017.
13. Scheinerman, Pickett y Coleman 2008.
14. Fomentar 2015.
15. Hardy y Wright 2008, teorema 193.
16. Thurston 2012.
17. Niven, Zuckerman y Montgomery 1991.
18. Martín 2004, pag. 557.
19. Afifi, Auroux y Karl 2018.
20. Sandifer 2006.
21. Euler 1748.

Referencias

• Afifi, Haitham; Auroux, Sébastien; Karl, Holger (abril de 2018). "MARVELO: Incrustación de red virtual inalámbrica para gráficos superpuestos con bucles". Conferencia de redes y comunicaciones inalámbricas IEEE 2018 (WCNC) . IEEE. págs. 1–6. arXiv : 1712.06676 . doi :10.1109/WCNC.2018.8377194. ISBN 978-1-5386-1734-2. S2CID  13447977.

• Bunder, Martín W.; Tonien, José (2017). "Expresiones en forma cerrada para dos fracciones continuas armónicas". La Gaceta Matemática . 101 (552): 439–448. doi :10.1017/mag.2017.125. S2CID  125489697.

• Chen, Chen-Fan; Shieh, Leang-San (1969). "Inversión de fracción continua por el algoritmo de Routh". Traducción IEEE. Teoría de circuitos . 16 (2): 197–202. doi :10.1109/TCT.1969.1082925.

• Collins, Darren C. (2001). «Fracciones continuas» (PDF) . Revista de Pregrado de Matemáticas del MIT . Archivado desde el original (PDF) el 20 de noviembre de 2001.

• Cuyt, A.; Brevik Petersen, V.; Verdonk, B.; Waadeland, H.; Jones, WB (2008). Manual de fracciones continuas para funciones especiales . Springer Verlag. ISBN 978-1-4020-6948-2.

• Encyclopædia Britannica (2013). "Fracción continua - matemáticas" . Consultado el 26 de abril de 2022 .

• Euler, Leonhard (1748). "E101 - Introductio in analysin infinitorum, volumen 1". El Archivo Euler . Consultado el 26 de abril de 2022 .

• Foster, Tony (22 de junio de 2015). "Teorema del día: Teorema nº 203" (PDF) . Robin Whitty. Archivado (PDF) desde el original el 11 de diciembre de 2013 . Consultado el 26 de abril de 2022 .

• Gragg, William B. (1974). "Interpretaciones matriciales y aplicaciones del algoritmo de fracción continua". Montañas Rocosas J. Matemáticas . 4 (2): 213. doi : 10.1216/RMJ-1974-4-2-213 . S2CID  121378061.

• Hardy, Godfrey H.; Wright, Edward M. (diciembre de 2008) [1979]. Introducción a la teoría de los números (6 ed.). Prensa de la Universidad de Oxford. ISBN 9780199219865.

• Heilermann, JBH (1846). "Ueber die Verwandlung von Reihen en Kettenbrüche". Journal für die reine und angewandte Mathematik . 33 : 174–188.

• Jones, William B.; Trono, WJ (1980). Fracciones continuas: teoría analítica y aplicaciones. Enciclopedia de Matemáticas y sus Aplicaciones . vol. 11. Lectura. Massachusetts: Compañía editorial Addison-Wesley. ISBN 0-201-13510-8.

• Khinchin, A. Ya. (1964) [Publicado originalmente en ruso, 1935]. Fracciones continuas . Prensa de la Universidad de Chicago . ISBN 0-486-69630-8.

• Long, Calvin T. (diciembre de 1972). Introducción elemental a la teoría de números (2ª ed.). Lexington: DC Heath y compañía . ISBN 9780669627039.

• Magnus, Arne (1962). "Fracciones continuas asociadas a la Tabla Padé". Matemáticas. Z. _ 78 : 361–374. doi :10.1007/BF01195180. S2CID  120535167.

• Martín, Richard M. (diciembre de 2004). Estructura Electrónica: Teoría Básica y Métodos Prácticos . Prensa de la Universidad de Cambridge. doi :10.1017/CBO9780511805769. ISBN 9780511805769.

• Niven, Iván; Zuckerman, Herbert S.; Montgomery, Hugh L. (1991). Una introducción a la teoría de números (Quinta ed.). Nueva York: Wiley . ISBN 0-471-62546-9.

• Perron, Oskar (1950). Die Lehre von den Kettenbrüchen . Nueva York, Nueva York: Chelsea Publishing Company.

• Pettofrezzo, Anthony J.; Byrkit, Donald R. (diciembre de 1970). Elementos de la teoría de números . Acantilados de Englewood: Prentice Hall . ISBN 9780132683005.

• Rieger, Georg Johann (1982). «Un nuevo enfoque de los números reales (motivado por fracciones continuas)» (PDF) . Abhandlungen der Braunschweigischen Wissenschaftlichen Gesellschaft . 33 : 205–217. Archivado (PDF) desde el original el 10 de diciembre de 2020.

• Rockett, Andrew M.; Szüsz, Peter (1992). Fracciones continuas . Prensa científica mundial. ISBN 981-02-1047-7.

• Sandifer, C. Edward (2006). "Capítulo 32: ¿Quién demostró que e es irracional?". Cómo lo hizo Euler (PDF) . Asociación Matemática de América . págs. 185-190. ISBN 978-0-88385-563-8. LCCN  2007927658. Archivado (PDF) desde el original el 19 de marzo de 2014.

• Scheinerman, Ed; Pickett, Thomas J.; Coleman, Ana (2008). "Otra fracción continua para π". El Mensual Matemático Estadounidense . 115 (10): 930–933. doi :10.1080/00029890.2008.11920610. JSTOR  27642639. S2CID  11914017.

• Zapatero, Ken (1995). "I.4: Aproximación Racional". En Paeth, Alan W. (ed.). Graphics Gems V (Versión IBM) . San Diego, California: Prensa académica. págs. 25-31. ISBN 0-12-543455-3.

• Siebeck, H. (1846). "Ueber periodische Kettenbrüche". Journal für die reine und angewandte Mathematik . 33 : 68–70.

• Thill, M. (2008). "Un algoritmo de redondeo más preciso para números racionales". Informática . 82 (2–3): 189–198. doi :10.1007/s00607-008-0006-7. S2CID  45166490.

• Thurston, Ben (2012). "Estimación de raíces cuadradas, expresión de fracción continua generalizada para cada raíz cuadrada". El blog de Ben Paul Thurston . Consultado el 26 de abril de 2022 .

• Muro, Hubert Stanley (1948). Teoría analítica de fracciones continuas . D. Van Nostrand Company, Inc. ISBN 0-8284-0207-8.

• Weisstein, Eric Wolfgang (2022). MathWorld (ed.). «Fracción continua periódica» . Consultado el 26 de abril de 2022 .

enlaces externos

• "Fracción continua", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]

• Knott, Ron (2018). "Fracciones continuas (hay disponible una calculadora de fracciones continuas combinadas en línea)" . Consultado el 26 de abril de 2022 .

• Linas Vepstas Continuad Fractions and Gaps (2004) revisa estructuras caóticas en fracciones continuas.
• Fracciones continuas en el árbol Stern-Brocot al cortar el nudo
• El mecanismo de Antikythera I: relaciones de transmisión y fracciones continuas Archivado el 4 de mayo de 2009 en la Wayback Machine.
• Calculadora de fracciones continuas, WIMS.
• Aritmética de fracciones continuas Primer artículo sobre fracciones continuas de Gosper, inédito. Almacenado en caché en la Wayback Machine de Internet Archive
• Weisstein, Eric W. "Fracción continua". MundoMatemático .
• Fracciones continuas de Stephen Wolfram y Aproximaciones de fracciones continuas de la función tangente de Michael Trott, Proyecto de demostraciones de Wolfram .
• Secuencia OEIS A133593 (fracción continua "exacta" para pi)
• Una visión de la "interpolación fraccionaria" de una fracción continua {1; 1, 1, 1, ...}
• Mejor aproximación racional mediante fracciones continuas
• FRACCIONES CONTINUAS de CD Olds