Claudio Ptolomeo ( griego : Πτολεμαῖος , Ptolemaios ; latín : Claudius Ptolemaeus ; c. 100 – c. 170 d. C.) [1] fue un matemático, astrónomo, astrólogo, geógrafo y teórico musical alejandrino [ 2 ] que escribió alrededor de una docena de tratados científicos , tres de los cuales fueron importantes para la ciencia bizantina , islámica y europea occidental posterior . El primero fue su tratado astronómico ahora conocido como Almagesto , originalmente titulado Tratado matemático ( griego : Μαθηματικὴ Σύνταξις , Mathēmatikḗ Syntaxis ). El segundo es la Geografía , que es una discusión exhaustiva sobre los mapas y el conocimiento geográfico del mundo grecorromano . El tercero es el tratado astrológico en el que intentó adaptar la astrología horoscópica a la filosofía natural aristotélica de su época. Esto a veces se conoce como Apotelesmatika ( griego : Αποτελεσματικά , lit. ' Sobre los efectos ' ) pero más comúnmente conocido como Tetrábiblos , del griego koiné que significa "Cuatro libros", o por su equivalente latino Quadripartite .
La Iglesia Católica promovió su trabajo, que incluía el único modelo geocéntrico matemáticamente sólido del Sistema Solar , y a diferencia de la mayoría de los matemáticos griegos , los escritos de Ptolomeo (principalmente el Almagesto ) nunca dejaron de ser copiados o comentados, tanto en la Antigüedad tardía como en la Edad Media . [3] Sin embargo, es probable que solo unos pocos dominaran verdaderamente las matemáticas necesarias para comprender sus obras, como lo evidencian particularmente las muchas introducciones abreviadas y diluidas a la astronomía de Ptolomeo que fueron populares entre los árabes y los bizantinos. [4] [5] Su trabajo sobre epiciclos ha llegado a simbolizar un modelo teórico muy complejo construido para explicar una suposición falsa.
Se desconoce la fecha y el lugar de nacimiento de Ptolomeo. El astrónomo del siglo XIV Teodoro Meliteniotes escribió que el lugar de nacimiento de Ptolomeo fue Ptolemais Hermiou , una ciudad griega en la región de la Tebaida de Egipto (actualmente El Mansha, Gobernación de Sohag ). Sin embargo, esta certificación es bastante tardía y no hay evidencia que la respalde. [6] [b]
Se sabe que Ptolomeo vivió en la ciudad de Alejandría o sus alrededores , en la provincia romana de Egipto bajo el dominio romano . [8] Tenía un nombre latino, Claudio, que generalmente implica que era ciudadano romano . [9] Estaba familiarizado con los filósofos griegos y utilizó las observaciones babilónicas y la teoría lunar babilónica. En la mitad de sus obras existentes, Ptolomeo se dirige a un tal Siro, una figura de la que casi no se sabe nada pero que probablemente compartía algunos de los intereses astronómicos de Ptolomeo. [10]
Ptolomeo murió en Alejandría alrededor del año 168. [ 11] (pág. 311)

El nombre griego de Ptolomeo , Ptolemaeus ( Πτολεμαῖος , Ptolemaîos ), es un antiguo nombre personal griego . Aparece una vez en la mitología griega y es de forma homérica . [12] Era común entre la clase alta macedonia en la época de Alejandro Magno y había varios con este nombre entre el ejército de Alejandro, uno de los cuales se autoproclamó faraón en el 323 a. C.: Ptolomeo I Sóter , el primer faraón del Reino ptolemaico . Casi todos los faraones posteriores de Egipto, con algunas excepciones, se llamaron Ptolomeos hasta que Egipto se convirtió en una provincia romana en el 30 a. C., poniendo fin al gobierno de la familia macedonia. [13]
El nombre Claudio es un nombre romano, perteneciente a la gens Claudia ; la peculiar forma multipartita del nombre completo Claudio Ptolomeo es una costumbre romana, característica de los ciudadanos romanos. Esto indica que Ptolomeo habría sido un ciudadano romano . [6] Gerald Toomer, el traductor del Almagesto de Ptolomeo al inglés, sugiere que la ciudadanía fue probablemente otorgada a uno de los antepasados de Ptolomeo por el emperador Claudio o el emperador Nerón . [14]
El astrónomo persa del siglo IX Abu Ma'shar al-Balkhi presenta erróneamente a Ptolomeo como miembro del linaje real del Egipto ptolemaico , afirmando que los descendientes del general alejandrino y faraón Ptolomeo I Sóter eran sabios "e incluían a Ptolomeo el Sabio, que compuso el libro del Almagesto ". Abu Ma'shar registró la creencia de que un miembro diferente de esta línea real "compuso el libro sobre astrología y lo atribuyó a Ptolomeo". La confusión histórica sobre este punto se puede inferir de la observación posterior de Abu Ma'shar: "A veces se dice que el hombre muy erudito que escribió el libro de astrología también escribió el libro del Almagesto . La respuesta correcta no se conoce". [15] No se conocen muchas pruebas positivas sobre el tema de la ascendencia de Ptolomeo, aparte de lo que se puede extraer de los detalles de su nombre, aunque los eruditos modernos han concluido que el relato de Abu Ma'shar es erróneo. [16] Ya no se duda de que el astrónomo que escribió el Almagesto también escribió el Tetrabiblos como su contraparte astrológica. [17] (p x ) En fuentes árabes posteriores , a menudo se le conocía como "el Alto Egipcio ", [18] [19] (p 606) lo que sugiere que puede haber tenido orígenes en el sur de Egipto . [19] (pp 602, 606) Los astrónomos , geógrafos y físicos árabes se refirieron a su nombre en árabe como Baṭlumyus ( árabe : بَطْلُمْيوس ). [20]
Ptolomeo escribió en griego koiné , [21] y se puede demostrar que utilizó datos astronómicos babilónicos . [22] [23] (p. 99) Podría haber sido un ciudadano romano, pero étnicamente era griego [1] [24] [25] o al menos un egipcio helenizado . [c] [26] [27]
La astronomía fue el tema al que Ptolomeo dedicó más tiempo y esfuerzo; aproximadamente la mitad de todas las obras que sobrevivieron tratan de cuestiones astronómicas, e incluso otras como la Geografía y el Tetrabiblos tienen referencias significativas a la astronomía. [5]

La Sintaxis matemática de Ptolomeo ( en griego : Μαθηματικὴ Σύνταξις , lit. « Tratado sistemático matemático » ), más conocida como Almagesto , es el único tratado antiguo completo que se conserva sobre astronomía. Aunque los astrónomos babilónicos habían desarrollado técnicas aritméticas para calcular y predecir fenómenos astronómicos, estas no se basaban en ningún modelo subyacente de los cielos; los primeros astrónomos griegos, por otro lado, proporcionaron modelos geométricos cualitativos para «salvar las apariencias» de los fenómenos celestiales sin la capacidad de hacer ninguna predicción. [28]
La primera persona que intentó fusionar estos dos enfoques fue Hiparco , quien produjo modelos geométricos que no solo reflejaban la disposición de los planetas y las estrellas, sino que también podían usarse para calcular los movimientos celestes. [23] Ptolomeo, siguiendo a Hiparco, derivó cada uno de sus modelos geométricos para el Sol, la Luna y los planetas a partir de observaciones astronómicas seleccionadas realizadas en un lapso de más de 800 años; sin embargo, muchos astrónomos han sospechado durante siglos que algunos de los parámetros de sus modelos se adoptaron independientemente de las observaciones. [29]
Ptolomeo presentó sus modelos astronómicos junto con tablas convenientes, que podían usarse para calcular la posición futura o pasada de los planetas. [30] El Almagesto también contiene un catálogo de estrellas , que es una versión de un catálogo creado por Hiparco . Su lista de cuarenta y ocho constelaciones es ancestral al sistema moderno de constelaciones pero, a diferencia del sistema moderno, no cubrían todo el cielo (solo lo que se podía ver a simple vista en el hemisferio norte). [31] Durante más de mil años, el Almagesto fue el texto autorizado sobre astronomía en Europa, Oriente Medio y el norte de África. [32]
El Almagesto se conservó, como muchas obras científicas griegas existentes, en manuscritos árabes ; se piensa que el título moderno es una corrupción árabe del nombre griego Hē Megistē Syntaxis (lit. "El tratado más grande"), como se conocía presumiblemente a la obra en la Antigüedad tardía . [33] Debido a su reputación, fue ampliamente buscado y traducido dos veces al latín en el siglo XII , una en Sicilia y otra en España. [34] Los modelos planetarios de Ptolomeo, como los de la mayoría de sus predecesores, eran geocéntricos y casi universalmente aceptados hasta la reaparición de los modelos heliocéntricos durante la revolución científica .
Bajo el escrutinio de la erudición moderna y la verificación cruzada de las observaciones contenidas en el Almagesto con las cifras producidas mediante extrapolación hacia atrás, han surgido varios patrones de errores dentro de la obra. [35] [36] Un error de cálculo destacado es el uso que hace Ptolomeo de mediciones que, según él, se tomaron al mediodía, pero que sistemáticamente producen lecturas que ahora se muestra que están desfasadas por media hora, como si las observaciones se hubieran tomado a las 12:30 p. m. [35]
La calidad general de las observaciones de Ptolomeo ha sido cuestionada por varios científicos modernos, pero de manera destacada por Robert R. Newton en su libro de 1977 El crimen de Claudio Ptolomeo , que afirmaba que Ptolomeo fabricó muchas de sus observaciones para que encajaran con sus teorías. [37] Newton acusó a Ptolomeo de inventar sistemáticamente datos o manipular los datos de astrónomos anteriores, y lo etiquetó como "el fraude más exitoso en la historia de la ciencia". [35] Un error sorprendente observado por Newton fue un equinoccio de otoño que se dice que fue observado por Ptolomeo y "medido con el mayor cuidado" a las 2 p. m. del 25 de septiembre de 132, cuando el equinoccio debería haber sido observado alrededor de las 9:55 a. m. del día anterior. [35] Al intentar refutar a Newton, Herbert Lewis también se encontró de acuerdo en que "Ptolomeo fue un fraude escandaloso" [36] y que "todos los resultados susceptibles de análisis estadístico apuntan más allá de toda duda hacia el fraude y contra el error accidental". [36]
Las acusaciones formuladas por Newton y otros han sido objeto de amplios debates y han recibido un importante rechazo de otros estudiosos en contra de los hallazgos. [35] Owen Gingerich , aunque está de acuerdo en que el Almagesto contiene "algunos números notablemente sospechosos", [35] incluso en el asunto del equinoccio desplazado de 30 horas, que señaló que se alineaba perfectamente con las predicciones hechas por Hiparco 278 años antes, [38] rechazó la calificación de fraude. [35] Bernard Goldstein también planteó objeciones , quien cuestionó los hallazgos de Newton y sugirió que había entendido mal la literatura secundaria, al tiempo que señaló que los problemas con la precisión de las observaciones de Ptolomeo se conocían desde hacía mucho tiempo. [37] Otros autores han señalado que la deformación de los instrumentos o la refracción atmosférica también pueden explicar algunas de las observaciones de Ptolomeo en un momento equivocado. [39] [40]
En 2022 se descubrieron los primeros fragmentos griegos del catálogo de estrellas perdido de Hiparco en un palimpsesto , lo que desacreditó las acusaciones realizadas por el astrónomo francés Delambre a principios del siglo XIX, que fueron repetidas por RR Newton. En concreto, demostró que Hiparco no era la única fuente del catálogo de Ptolomeo, como ambos habían afirmado, y demostró que Ptolomeo no se limitó a copiar las mediciones de Hiparco y ajustarlas para tener en cuenta la precesión de los equinoccios, como habían afirmado. Los científicos que analizaron los gráficos concluyeron:
También confirma que el Catálogo de estrellas de Ptolomeo no se basó únicamente en datos del Catálogo de Hiparco.
... Estas observaciones son consistentes con la opinión de que Ptolomeo compuso su catálogo de estrellas combinando varias fuentes, incluido el catálogo de Hiparco, sus propias observaciones y, posiblemente, las de otros autores. [41]
Las Tablas Prácticas ( en griego : Πρόχειροι κανόνες ) son un conjunto de tablas astronómicas, junto con cánones para su uso. Para facilitar los cálculos astronómicos, Ptolomeo tabuló todos los datos necesarios para calcular las posiciones del Sol, la Luna y los planetas, la salida y puesta de las estrellas y los eclipses de Sol y Luna, convirtiéndolas en una herramienta útil para astrónomos y astrólogos. Las tablas en sí son conocidas a través de la versión de Teón de Alejandría . Aunque las Tablas Prácticas de Ptolomeo no sobreviven como tales en árabe o en latín, representan el prototipo de la mayoría de las tablas astronómicas árabes y latinas o zījes . [42]
Además, la introducción a las Tablas Prácticas sobrevivió por separado de las tablas mismas (aparentemente parte de una recopilación de algunos de los escritos más breves de Ptolomeo) bajo el título Disposición y cálculo de las Tablas Prácticas . [43]
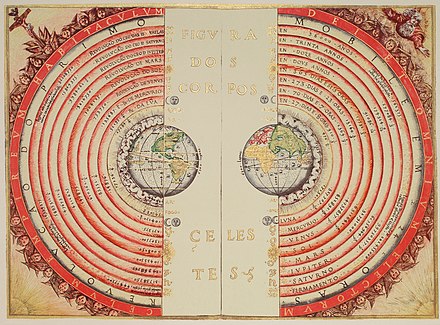
Las Hipótesis Planetarias ( en griego : Ὑποθέσεις τῶν πλανωμένων , lit. ' Hipótesis de los Planetas ' ) es una obra cosmológica , probablemente una de las últimas escritas por Ptolomeo, en dos libros que tratan sobre la estructura del universo y las leyes que gobiernan el movimiento celeste . [44] Ptolomeo va más allá de los modelos matemáticos del Almagesto para presentar una realización física del universo como un conjunto de esferas anidadas, [45] en la que utilizó los epiciclos de su modelo planetario para calcular las dimensiones del universo. Estimó que el Sol estaba a una distancia media de 1 210 radios terrestres (ahora se sabe que en realidad son ~23 450 radios), mientras que el radio de la esfera de las estrellas fijas era 20 000 veces el radio de la Tierra. [46]
La obra también es notable por tener descripciones sobre cómo construir instrumentos para representar los planetas y sus movimientos desde una perspectiva geocéntrica , de forma muy similar a lo que un orrery habría hecho para uno heliocéntrico , presumiblemente con fines didácticos. [47]
El Analema es un breve tratado en el que Ptolomeo proporciona un método para especificar la ubicación del Sol en tres pares de arcos de coordenadas orientados localmente en función de la declinación del Sol, la latitud terrestre y la hora. La clave del enfoque es representar la configuración sólida en un diagrama plano que Ptolomeo llama analema . [48]
En otra obra, Phaseis ( Amanecimientos de las estrellas fijas ), Ptolomeo presentó un parapegma , un calendario estelar o almanaque , basado en las apariciones y desapariciones de las estrellas a lo largo del año solar. [49]
El Planisphaerium ( griego : Ἅπλωσις ἐπιφανείας σφαίρας , lit. ' Aplanamiento de la esfera ' ) contiene 16 proposiciones que tratan de la proyección de los círculos celestes sobre un plano. El texto se ha perdido en griego (excepto un fragmento) y sólo sobrevive en árabe y latín. [50]
Ptolomeo también erigió una inscripción en un templo de Canopo , alrededor de 146-147 d. C., conocida como la Inscripción Canóbica . Aunque la inscripción no ha sobrevivido, alguien en el siglo VI la transcribió, y copias manuscritas la preservaron a lo largo de la Edad Media. Comienza: "Al dios salvador, Claudio Ptolomeo (dedica) los primeros principios y modelos de astronomía", seguido de un catálogo de números que definen un sistema de mecánica celeste que gobierna los movimientos del Sol, la Luna, los planetas y las estrellas. [51]
En 2023, los arqueólogos pudieron leer un manuscrito que da instrucciones para la construcción de una herramienta astronómica llamada meteoroscopio ( μετεωροσκόπιον o μετεωροσκοπεῖον ). El texto, que proviene de un manuscrito del siglo VIII que también contiene el Analema de Ptolomeo , fue identificado tanto por su contenido como por su análisis lingüístico como obra de Ptolomeo. [52] [53]

La segunda obra más conocida de Ptolomeo es su Geographike Hyphegesis ( griego : Γεωγραφικὴ Ὑφήγησις ; lit. ' Guía para dibujar la Tierra ' ), conocida como Geografía , un manual sobre cómo dibujar mapas utilizando coordenadas geográficas para partes del mundo romano conocidas en ese momento. [54] [55] Se basó en trabajos previos de un geógrafo anterior, Marino de Tiro , así como en diccionarios geográficos del Imperio romano y el antiguo Imperio persa . [55] [54] También reconoció al antiguo astrónomo Hiparco por haber proporcionado la elevación del polo norte celeste [56] para algunas ciudades. Aunque los mapas basados en principios científicos se habían hecho desde la época de Eratóstenes ( c. 276 - c. 195 a. C. ), Ptolomeo mejoró las proyecciones cartográficas .
La primera parte de la Geografía es una discusión de los datos y de los métodos que utilizó. Ptolomeo destaca la supremacía de los datos astronómicos sobre las mediciones terrestres o los informes de los viajeros, aunque poseía estos datos para solo un puñado de lugares. La verdadera innovación de Ptolomeo, sin embargo, ocurre en la segunda parte del libro, donde proporciona un catálogo de 8.000 localidades que recopiló de Marinus y otros, la base de datos más grande de este tipo de la antigüedad. [ 57] Aproximadamente 6.300 de estos lugares y características geográficas tienen coordenadas asignadas para que puedan ubicarse en una cuadrícula que abarca el globo. [5] La latitud se medía desde el ecuador , como se hace hoy, pero Ptolomeo prefería expresarla como climata , la longitud del día más largo en lugar de grados de arco : La duración del día de pleno verano aumenta de 12 h a 24 h a medida que uno va del ecuador al círculo polar . [58] Uno de los lugares para los que Ptolomeo anotó coordenadas específicas fue la torre de piedra ahora perdida que marcaba el punto medio de la antigua Ruta de la Seda , y que los eruditos han estado tratando de localizar desde entonces. [59]
En la tercera parte de la Geografía , Ptolomeo da instrucciones sobre cómo crear mapas tanto de todo el mundo habitado ( oikoumenē ) como de las provincias romanas, incluyendo las listas topográficas necesarias y los títulos de los mapas. Su oikoumenē abarcaba 180 grados de longitud desde las Islas Benditas en el océano Atlántico hasta el centro de China , y unos 80 grados de latitud desde Shetland hasta Anti-Meroe (costa este de África ); Ptolomeo era muy consciente de que conocía sólo una cuarta parte del globo, y una extensión errónea de China hacia el sur sugiere que sus fuentes no llegaban hasta el océano Pacífico. [54] [55]
Parece probable que las tablas topográficas de la segunda parte de la obra (libros 2-7) sean textos acumulativos, que fueron alterados a medida que se disponía de nuevos conocimientos en los siglos posteriores a Ptolomeo. [60] Esto significa que es probable que la información contenida en diferentes partes de la Geografía sea de fechas diferentes, además de contener muchos errores de copista. Sin embargo, aunque los mapas regionales y mundiales de los manuscritos supervivientes datan de alrededor de 1300 d. C. (después de que el texto fuera redescubierto por Maximus Planudes ), hay algunos estudiosos que piensan que dichos mapas se remontan al propio Ptolomeo. [57]

Ptolomeo escribió un tratado astrológico, en cuatro partes, conocido por el término griego Tetrabiblos (lit. "Cuatro Libros") o por su equivalente latino Quadripartitum . [61] Su título original es desconocido, pero puede haber sido un término encontrado en algunos manuscritos griegos, Apotelesmatiká ( biblía ), que significa aproximadamente "(libros) sobre los Efectos" o "Resultados", o "Pronósticos". [17] (p x ) Como fuente de referencia, se dice que el Tetrabiblos "gozó casi de la autoridad de una Biblia entre los escritores astrológicos de mil años o más". [17] (p xii ) Fue traducido por primera vez del árabe al latín por Platón de Tívoli (Tiburtino) en 1138, mientras estaba en España. [62]
Gran parte del contenido del Tetrabiblos fue recopilado de fuentes anteriores; el logro de Ptolomeo fue ordenar su material de manera sistemática, mostrando cómo el tema podía, en su opinión, ser racionalizado. De hecho, se presenta como la segunda parte del estudio de la astronomía del cual el Almagesto fue el primero, relacionado con las influencias de los cuerpos celestes en la esfera sublunar . [4] [16] De esta manera, se proporcionan explicaciones de algún tipo para los efectos astrológicos de los planetas , basadas en sus efectos combinados de calentamiento, enfriamiento, humectación y secado. [63] Ptolomeo descarta otras prácticas astrológicas, como considerar el significado numerológico de los nombres, que creía que no tenían una base sólida, y deja de lado temas populares, como la astrología electiva (interpretación de cartas astrales para determinar cursos de acción) y la astrología médica , por razones similares. [64]
El gran respeto que los astrólogos posteriores tuvieron por el Tetrabiblos se derivó de su naturaleza como exposición de teoría, más que como manual. [64]
Una colección de cien aforismos sobre astrología llamada Centiloquium , atribuida a Ptolomeo, fue ampliamente reproducida y comentada por eruditos árabes, latinos y hebreos, y a menudo unida en manuscritos medievales después del Tetrabiblos como una especie de resumen. [5] Ahora se cree que es una composición pseudoepigráfica mucho más tardía . La identidad y la fecha del autor real de la obra, al que ahora se hace referencia como Pseudo-Ptolomeo , sigue siendo objeto de conjeturas. [65]

Ptolomeo escribió una obra titulada Harmonikon ( griego : Ἁρμονικόν , conocida como los Armónicos , sobre la teoría musical y las matemáticas detrás de las escalas musicales en tres libros. [66]
Armónicos comienza con una definición de la teoría armónica, con una larga exposición sobre la relación entre la razón y la percepción sensorial para corroborar los supuestos teóricos. Después de criticar los planteamientos de sus predecesores, Ptolomeo aboga por basar los intervalos musicales en proporciones matemáticas (en contraposición a las ideas defendidas por los seguidores de Aristóxeno ), respaldadas por la observación empírica (en contraste con el enfoque excesivamente teórico de los pitagóricos ). [67] [68]
Ptolomeo introduce el canon armónico (nombre griego) o monocordio (nombre latino), que es un aparato musical experimental que utilizó para medir tonos relativos, y utilizó para describir a sus lectores cómo demostrar las relaciones discutidas en los siguientes capítulos por sí mismos. Después de la exposición temprana sobre cómo construir y usar el monocordio para probar los sistemas de afinación propuestos, Ptolomeo procede a discutir la afinación pitagórica (y cómo demostrar que su escala musical idealizada falla en la práctica). Los pitagóricos creían que las matemáticas de la música deberían basarse solo en la proporción específica de 3:2, la quinta perfecta , y creían que las afinaciones matemáticamente exactas a su sistema resultarían melodiosas, si solo pudieran calcularse (a mano) los números extremadamente grandes involucrados. Por el contrario, Ptolomeo creía que las escalas musicales y las afinaciones deberían, en general, involucrar múltiples proporciones diferentes organizadas para encajar uniformemente en tetracordios más pequeños (combinaciones de cuatro proporciones de tonos que juntas forman una cuarta perfecta ) y octavas . [69] [70] Ptolomeo revisó la práctica de afinación musical estándar (y antigua, en desuso) de su época, que luego comparó con sus propias subdivisiones del tetracordio y la octava , que derivó experimentalmente utilizando un canon monocordio /armónico. El volumen termina con una exposición más especulativa de las relaciones entre la armonía, el alma ( psique ) y los planetas ( armonía de las esferas ). [71]
Aunque la Armónica de Ptolomeo nunca tuvo la influencia de su Almagesto o Geografía , es, no obstante, un tratado bien estructurado y contiene más reflexiones metodológicas que cualquier otro de sus escritos. En particular, es una forma naciente de lo que en el siguiente milenio se desarrolló en el método científico, con descripciones específicas del aparato experimental que construyó y utilizó para probar conjeturas musicales, y las relaciones musicales empíricas que identificó al probar tonos entre sí: Pudo medir con precisión los tonos relativos basándose en las proporciones de las longitudes vibratorias de dos lados separados de la misma cuerda , por lo que se aseguró que estuvieran bajo la misma tensión, eliminando una fuente de error. Analizó las proporciones determinadas empíricamente de pares de tonos "agradables", y luego las sintetizó todas en una descripción matemática coherente, que persiste hasta el presente como entonación justa , el estándar para la comparación de la consonancia en los muchos otros sistemas de afinación de compromiso menos que exactos pero más fáciles . [72] [73]
Durante el Renacimiento , las ideas de Ptolomeo inspiraron a Kepler en sus propias reflexiones sobre la armonía del mundo ( Harmonice Mundi , Apéndice del Libro V). [74]
La Optica ( griego koiné : Ὀπτικά ), conocida como la Óptica, es una obra que sobrevive solo en una versión latina algo pobre, que, a su vez, fue traducida de una versión árabe perdida por Eugenio de Palermo ( c. 1154 ). En ella, Ptolomeo escribe sobre las propiedades de la vista (no de la luz), incluyendo la reflexión , la refracción y el color . La obra es una parte significativa de la historia temprana de la óptica e influyó en el más famoso y superior Libro de Óptica del siglo XI de Ibn al-Haytham . [75] Ptolomeo ofreció explicaciones para muchos fenómenos relacionados con la iluminación y el color, el tamaño, la forma, el movimiento y la visión binocular. También dividió las ilusiones en aquellas causadas por factores físicos u ópticos y aquellas causadas por factores de juicio. Ofreció una explicación oscura de la ilusión del Sol o la Luna (el tamaño aparente agrandado en el horizonte) basada en la dificultad de mirar hacia arriba. [76] [77]
La obra se divide en tres secciones principales. La primera sección (libro II) trata de la visión directa a partir de los primeros principios y termina con un análisis de la visión binocular. La segunda sección (libros III-IV) trata de la reflexión en espejos planos, convexos, cóncavos y compuestos. [78] La última sección (libro V) trata de la refracción e incluye la tabla de refracción del aire al agua más antigua que se conserva, cuyos valores (con excepción del ángulo de incidencia de 60°) muestran signos de haber sido obtenidos a partir de una progresión aritmética. [79] Sin embargo, según Mark Smith, la tabla de Ptolomeo se basaba en parte en experimentos reales. [80]
La teoría de la visión de Ptolomeo consistía en rayos (o flujo) que provenían del ojo formando un cono, cuyo vértice se encontraba dentro del ojo y cuya base definía el campo visual. Los rayos eran sensibles y transmitían información al intelecto del observador sobre la distancia y la orientación de las superficies. El tamaño y la forma estaban determinados por el ángulo visual subtendido en el ojo combinado con la distancia y la orientación percibidas. [75] [81] Esta fue una de las primeras afirmaciones de la invariancia tamaño-distancia como causa de la constancia perceptual del tamaño y la forma, una visión apoyada por los estoicos. [82]
Aunque es conocido principalmente por sus contribuciones a la astronomía y otros temas científicos, Ptolomeo también participó en discusiones epistemológicas y psicológicas en todo su corpus. [83] Escribió un breve ensayo titulado Sobre el criterio y el hegemonikon ( griego : Περὶ Κριτηρίου καὶ Ἡγεμονικοῡ ), que puede haber sido uno de sus primeros trabajos. Ptolomeo trata específicamente sobre cómo los humanos obtienen conocimiento científico (es decir, el "criterio" de la verdad), así como sobre la naturaleza y estructura de la psique o alma humana, particularmente su facultad gobernante (es decir, el hegemonikon ). [71] Ptolomeo argumenta que, para llegar a la verdad, uno debe usar tanto la razón como la percepción sensorial de maneras que se complementen entre sí. Sobre el criterio también es notable por ser la única obra de Ptolomeo que carece de matemáticas . [84]
En otros pasajes, Ptolomeo afirma la supremacía del conocimiento matemático sobre otras formas de conocimiento. Al igual que Aristóteles antes que él, Ptolomeo clasifica las matemáticas como un tipo de filosofía teórica; sin embargo, Ptolomeo cree que las matemáticas son superiores a la teología o la metafísica porque estas últimas son conjeturales mientras que solo las primeras pueden asegurar un conocimiento seguro. Esta visión es contraria a las tradiciones platónica y aristotélica , donde la teología o la metafísica ocupaban el más alto honor. [83] A pesar de ser una posición minoritaria entre los filósofos antiguos, las opiniones de Ptolomeo fueron compartidas por otros matemáticos como Herón de Alejandría . [85]
Hay varios personajes y objetos que llevan el nombre de Ptolomeo, entre ellos:
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ){{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )