Media aritmética
La media aritmética es un concepto matemático usado en estadística.
Además de en matemáticas y estadística, la media aritmética se utiliza con frecuencia en economía, antropología, historia y en cierta medida en casi todos los campos académicos.
Aunque la media aritmética se utiliza a menudo para informar de las tendencias centrales, no es una estadística robusta: está muy influida por los valores atípicos (valores mucho mayores o menores que la mayoría de los demás).
En ese caso, las estadísticas robustas, como la mediana, pueden proporcionar una mejor descripción de la tendencia central.
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra x con una barra horizontal sobre el símbolo para representar la media de una muestra (
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
La media aritmética puede definirse de forma similar para vectores en múltiples dimensiones, no sólo para valores escalares; a menudo se denomina centroide.
al conjunto de datos escalable métricamente
Entonces el nuevo valor medio del conjunto de datos será
Por ejemplo, es fácil deducir que en una reunión de 38 individuos hay necesariamente al menos 4 que nacieron el mismo mes.
El promedio de individuos que nacieron por mes es 38/12 ≈ 3,167.
Luego en algún mes nacieron en una cantidad entera y mayor o igual que el promedio, o sea 4 ≥ 3,167.
[1] La media aritmética tiene varias propiedades que la hacen interesante, especialmente como medida de tendencia central.
Entre ellas se encuentran: La media aritmética puede contrastarse con la mediana.
Si los elementos de los datos incrementan aritméticamente cuando se colocan en algún orden, entonces la mediana y la media aritmética son iguales.
, la mediana y la media aritmética pueden diferir significativamente.
Existen aplicaciones de este fenómeno en muchos campos.
[3] Una media ponderada, o promedio ponderado, es un promedio en el que algunos puntos de datos cuentan más que otros en el sentido de que se les da más peso en el cálculo.
Por el contrario, una media ponderada en la que el primer número recibe, por ejemplo, el doble de peso que el segundo (quizás porque se supone que aparece el doble de veces en la población general de la que se extrajeron estos números) se calcularía como
Aquí los pesos, que necesariamente suman uno, son
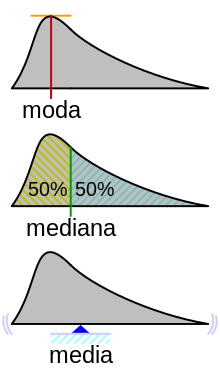
La distribución de probabilidad más extendida se denomina distribución normal; tiene la propiedad de que todas las medidas de su tendencia central, incluyendo no sólo la media, sino también la mediana mencionada anteriormente y la moda (las tres M[5]), son iguales.
Esta igualdad no se cumple para otras distribuciones de probabilidad, como se ilustra aquí para la distribución log-normal.
Hay que tener especial cuidado cuando se utilizan datos cíclicos, como fases o ángulos.
Esto es incorrecto por dos razones: En la aplicación general, un descuido de este tipo hará que el valor medio se desplace artificialmente hacia la mitad del intervalo numérico.
Una solución a este problema es utilizar la formulación de optimización (es decir, definir la media como el punto central: el punto en torno al cual se tiene la menor dispersión) y redefinir la diferencia como una distancia modular (es decir, la distancia en el círculo: así, la distancia modular entre 1° y 359° es 2°, no 358°).
La media aritmética suele denotarse mediante una barra (vinculum o macron), como en
[2] Es posible que algunos programas (procesadores de texto, navegadores webs) no muestren correctamente el símbolo "x̄".
Por ejemplo, el símbolo HTML "x̄" combina dos códigos: la letra base "x" más un código para la línea superior (̄ o ¯).
[6] En algunos formatos de documento (como PDF), el símbolo puede ser sustituido por un símbolo "¢" (cent) cuando se copia en un procesador de texto como Microsoft Word.