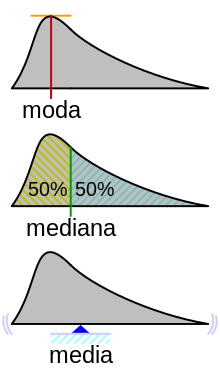
Moda (estadística)
En estadística, la moda es el valor que aparece con mayor frecuencia en un conjunto de datos.
Esto va en forma de una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima.
Una distribución trimodal de los datos es en la que encontramos tres modas.
En el caso de la distribución uniforme discreta, cuando todos los datos tienen una misma frecuencia, se puede definir las modas como indicado, pero estos valores no tienen utilidad.
En otras palabras, es el valor que tiene más probabilidades de ser muestreado.
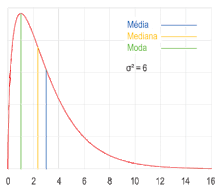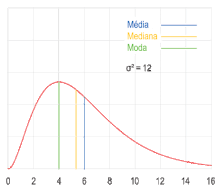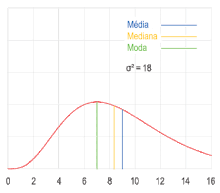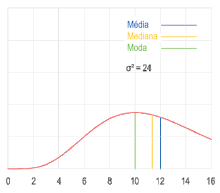
Una distribución continua de este tipo se denomina multimodal (por oposición a unimodal).
[1] Asimismo, la moda se aplicó por primera vez en el trading técnico, mediante el concepto de moda móvil (MM), ideado por el español Pedro L. Asensio Álvarez, donde establece como concepto para su desarrollo "la moda es el precio más frecuente para un período determinado".
Aunque hubiera errores, la mayoría de los sitiados habría acertado en los recuentos.
Es decir, el gran número de recuentos habría sido fiable.
[6] El modo de una muestra es el elemento que aparece con más frecuencia en la colección.
Para una muestra de una distribución continua, como [0,935..., 1,211..., 2,430..., 3,668..., 3,874...], el concepto es inutilizable en su forma bruta, ya que no habrá dos valores exactamente iguales, por lo que cada valor ocurrirá precisamente una vez.
El siguiente ejemplo de código MATLAB (o Octave) calcula la moda de una muestra: El algoritmo requiere como primer paso ordenar la muestra en orden ascendente.
Por ejemplo, si tomamos una muestra de Nombre de familia coreano, podríamos encontrar que "Kim" aparece con más frecuencia que cualquier otro nombre.
En cualquier sistema de votación en el que una pluralidad determina la victoria, un único valor modal determina el vencedor, mientras que un resultado multimodal requeriría algún procedimiento de desempate.
Para algunas distribuciones de probabilidades, el valor esperado puede ser infinito o indefinido, pero si está definido, es único.
No es necesariamente única, pero nunca infinita o totalmente indefinida.
Por último, como ya se ha dicho, la moda no es necesariamente única.
Para obtener la moda en datos agrupados se usa la siguiente fórmula: Donde: Sus principales propiedades son: