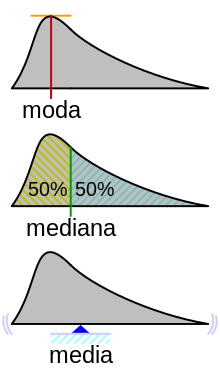
Mediana (estadística)
Por ejemplo, la siguiente lista de siete números, tiene como mediana 6, que es el cuarto valor.
Si el conjunto de datos tiene un número par de observaciones, no hay un valor medio distinto y la mediana suele definirse como la media aritmética de los dos valores medios.
(En términos más técnicos, esto interpreta la mediana como el estimador completamente recortado rango medio).
En general, con esta convención, la mediana puede definirse como sigue: Para un conjunto de datos
La mediana se utiliza normalmente para dar un valor "típico" que caracteriza un conjunto de datos.
Un ejemplo de esta situación se da al analizar el tiempo que los estudiantes universitarios tardan en acabar una carrera, el hecho que haya algunos estudiantes que estén muchos años para acabar la carrera (porque se ponen a trabajar y retardan los estudios, u otros motivos) hace que la media no refleje bien los datos; al contrario, la mediana no es sensible a estos valores extremos, y proporciona un mejor valor representativo de la duración de los estudios.
Formalmente, una mediana de una población es cualquier valor tal que al menos la mitad de la población es menor o igual que la mediana propuesta y al menos la mitad es mayor o igual que la mediana propuesta.
Como se ha visto anteriormente, las medianas pueden no ser únicas.
Por tanto, la mediana puede aplicarse a clases ordenadas pero no numéricas (por ejemplo, calcular la mediana de una nota cuando los alumnos se califican de A a F), aunque el resultado podría estar a medio camino entre las clases si hay un número par de casos.
Una mediana geométrica, en cambio, se define en cualquier número de dimensiones.
No existe una notación estándar ampliamente aceptada para la mediana, pero algunos autores representan la mediana de una variable x bien como x͂ o como μ1/2[2] a veces también M.[4][5] En cualquiera de estos casos, el uso de estos u otros símbolos para la mediana debe definirse explícitamente cuando se introducen.
La mediana se puede utilizar como una medida de localización cuando uno concede poca importancia a los valores extremos, normalmente porque una distribución es skewed, los valores extremos no son conocidos, o outliers son poco fiables, es decir, pueden ser errores de medición/transcripción.
Sin embargo, la relación empírica ampliamente citada de que la media se desplaza "más hacia la cola" de una distribución que la mediana no suele ser cierta.
Como mucho, se puede decir que las dos estadísticas no pueden estar "demasiado lejos".
[6] Como la mediana se basa en los datos medios de un conjunto, no es necesario conocer el valor de los resultados extremos para calcularla.
Por ejemplo, en una prueba de psicología en la que se investiga el tiempo necesario para resolver un problema, si un pequeño número de personas no consigue resolver el problema en absoluto en el tiempo dado, se puede calcular la mediana.
[7] Debido a que la mediana es sencilla de entender y fácil de calcular, a la vez que una aproximación robusta a la media, la mediana es una estadística de resumen popular en estadística descriptiva.
En este contexto, hay varias opciones para una medida de variabilidad: el rango, el rango intercuartílico, la desviación media y la desviación absoluta mediana.
Aunque no suele ser óptima si se supone una distribución poblacional determinada, sus propiedades son siempre razonablemente buenas.
Incluso entonces, la mediana tiene una eficiencia del 64% en comparación con la media de varianza mínima (para muestras normales grandes), lo que equivale a decir que la varianza de la mediana será ~50% mayor que la varianza de la media.
[8][9] Existen dos métodos para el cálculo de la mediana: Sean
, distinguimos dos casos: a) Si n es impar, la mediana es el valor que ocupa la posición
Por ejemplo, si tenemos 5 datos, que ordenados son:
b) Si n es par, la mediana es la media aritmética de los dos valores centrales.
es par, los dos datos que están en el centro de la muestra ocupan las posiciones
y otros dos que quedan por encima del siguiente dato
es la amplitud de los intervalos seleccionados para el diagrama.
Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene
Así, aplicando la fórmula asociada a la mediana para
Con lo cual la mediana será la media aritmética de los valores de la variable que ocupen el decimonoveno y el vigésimo lugar.