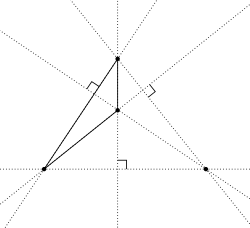
Sistema ortocéntrico
Estos cuatro triángulos posibles tendrán la misma circunferencia de los nueve puntos.
En consecuencia, estos cuatro triángulos posibles deben tener circunferencias circunscritas con el mismo circunradio.
[1] Si los seis conectores que unen cualquier par de puntos ortocéntricos se extienden a seis líneas que se cruzan entre sí, generan siete puntos de intersección.
Además, los tres puntos restantes se convierten en los excentros de este triángulo órtico común.
Los seis conectores mencionados anteriormente son AB, AC, BC, AH, BH y CH.
Las siete intersecciones mencionadas anteriormente son A, B, C, H (los puntos ortocéntricos originales) y HA, HB, HC (los pies de las alturas del triángulo ABC y los vértices del triángulo órtico).
Ahora considérense los otros tres triángulos posibles, ABH, ACH y BCH.
En un sistema ortocéntrico normalizado, la incónica órtica que es tangente a los lados del triángulo ABC es un inelipse y las incónicas órticas de los otros tres triángulos posibles son hipérbolas.
Hay muchas curvas cúbicas documentadas que pasan por un triángulo de referencia y su ortocentro.
La circuncúbica conocida como ortocúbica - K006 es interesante porque pasa a través de los tres sistemas ortocéntricos, así como por los tres vértices del triángulo órtico (pero no por el ortocentro del triángulo órtico).