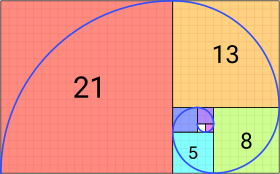
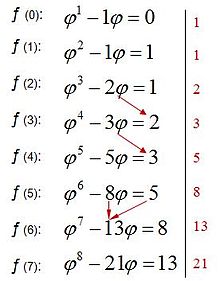Sucesión de Fibonacci
Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci.
La sucesión fue descrita y dada a conocer en occidente por Fibonacci ejemplificándolo con la solución a un problema de la cría de conejos, dando inicio a ese simpático mito de que así la descubriera.
Fue un divulgador y estudioso de la matemática indo-arábiga aprendida en Alejandría, Argelia, Bujía y otras ciudades del mediterráneo sur, exponiendo múltiples aplicaciones prácticas de una matemática desconocida en Occidente, como los numerales árabes (con un sistema de numeración decimal, notación posicional y un dígito de valor nulo: el cero), con énfasis en su uso en contabilidad, física y pedagogía y disciplina matemática, tanto que la República de Pisa lo honra concediéndole un salario permanente en agradecimiento a sus servicios asesorando en materias de contabilidad a la ciudad y enseñado a los ciudadanos.
[5] Parmanand Singh cita a Pingala (hacia 450) como precursor en el descubrimiento de la secuencia.
De esta manera Fibonacci presentó la sucesión en su libro Liber Abaci, publicado en 1202.
[7] También Kepler describió los números de Fibonacci, y el matemático escocés Robert Simson descubrió en 1753 que la relación entre dos números de Fibonacci sucesivos
Esta sucesión tuvo popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores con tanto renombre como Béla Bartók, Olivier Messiaen, la banda Tool y Delia Derbyshire la utilizaron para la creación de acordes y de nuevas estructuras de frases musicales.
Esto produce los siguientes números: y así sucesivamente.
Para simplificar aún más es necesario considerar el número áureo de manera que la ecuación (5) se reduce a (6)
Esta fórmula, conocida como fórmula de Binet se le atribuye al matemático francés Édouard Lucas, y es fácilmente demostrable por inducción matemática.
), la fórmula puede escribirse, eliminando este segundo sumando, así: (7)
que no tienen ceros consecutivos y en una vasta cantidad de contextos diferentes.
Se trata de un tributo a la amplitud con la que los números de Fibonacci aparecen en matemática y sus aplicaciones en otras áreas.
En este sentido la sucesión puede expandirse al conjunto de los números enteros como
Para poder definir los índices negativos de la sucesión, se despeja
Una sucesión de fibonacci generalizada muy importante, es la formada por las potencias del número áureo.
es una sucesión de Fibonacci generalizada, entonces Por ejemplo, la ecuación (11) puede generalizarse a Esto significa que cualquier cálculo sobre una sucesión de Fibonacci generalizada se puede efectuar usando números de Fibonacci.
Su definición misma puede emplearse como uno de estos algoritmos, aquí expresado en pseudocódigo: función
Para evitar hacer tantas operaciones, es común recurrir a una calculadora y utilizar la ecuación (6) del matemático Édouard Lucas.
Por ejemplo, si se usa una calculadora de 10 dígitos, entonces la fórmula anterior arroja como resultado
Este error se hace cada vez más grande conforme crece
De igual forma se puede crear una función utilizando la fórmula, muy eficiente,
Este método es el que se usaría normalmente para hacer el cálculo con lápiz y papel.
Por ejemplo, en el algoritmo 3 solo se requiere efectuar 50 sumas para calcular
Un algoritmo todavía más rápido se deduce partiendo de la ecuación (10).
Sin embargo, no es necesario almacenar los cuatro valores de cada matriz dado que cada una tiene la forma De esta manera, cada matriz queda completamente representada por los valores
[14] Sin embargo, también se han hecho muchas invocaciones infundadas a la aparición de los números de Fibonacci aprovechando su relación con el número áureo en la literatura popular.
Debido a que el coeficiente es un número irracional, ninguna semilla tiene ninguna vecina al mismo ángulo respecto al centro, por lo que se compactan eficientemente.
Debido a que las aproximaciones racionales al número aúreo son de la forma F(j):F(j + 1), los vecinos más próximos al número de semillas n están todos en n ± F(j) para cada índice j, que depende de r, la distancia al centro.
El hecho es que un zángano (1), el macho de la abeja, no tiene padre, pero sí que tiene una madre (1, 1), dos abuelos, que son los padres de la reina (1, 1, 2), tres bisabuelos, ya que el padre de la reina no tiene padre (1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5), ocho trastatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente, cumpliendo con la sucesión de Fibonacci.