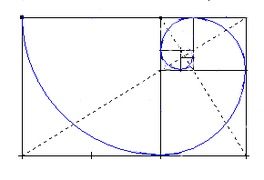
Rectángulo dorado
En la matemática clásica se construye a partir de la regla y compás siguiendo los pasos: De acuerdo con el matemático y divulgador científico Mario Greco, desde la publicación del libro de Luca Pacioli titulado Divina Proportione in 1509,[2] Fue cuando la razón dorada aparece descrita en los tratados de arte y de arquitectura,"[3] haciendo que muchos artistas y arquitectos emplearan su cantidad en el diseño por considerarlo estéticamente agradable.
[4] Si la longitud del lado mayor se denomina x, se tiene entonces por definición que se respeta la siguiente igualdad: Esto lleva a tener que resolver la ecuación de segundo grado: En la que una de las dos raíces es la proporción dorada.
El rectángulo cuyos vértices se definen por los puntos AEFD se define como áureo debido a que sus lado mayor AE y su lado corto AD presentan la proporción del número áureo.
El matemático griego Euclides, en su proposición 2.11 de la obra Los elementos, obtiene su construcción.
Siendo el triángulo GBC pitagórico, se tiene que GC (la hipotenusa) tiene como valor: Con centro en G, prolongando hasta la recta AE, se obtiene por intersección el punto E, y por lo tanto: con todo ello se puede ver que resulta evidente que los lados: de donde, finalmente: Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que este último es asimismo un rectángulo áureo.