Fórmula de rotación de Rodrigues

Si v es un vector en ℝ3 y k es un vector unitario que describe un eje de rotación sobre el cual v gira en un ángulo θ según la regla de la mano derecha, la fórmula de Rodrigues para el vector girado vrot es

Una definición alternativa es escribir el vector del eje como un producto vectorial a × b de cualquiera de los dos vectores distintos a cero a y b que definen el plano de rotación, y el sentido del ángulo θ se mide desde a y hacia b.

Al dejar que α denote el ángulo entre estos vectores, los dos ángulos θ y α no son necesariamente iguales, pero se miden en el mismo sentido.

Entonces el vector del eje unitario se puede escribir Esta forma puede ser más útil cuando están involucrados dos vectores que definen un plano.

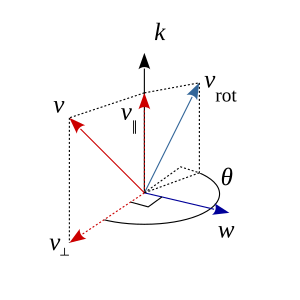
Sea k un vector unitario definiendo un eje de rotación, y sea v un vector para rotar sobre k por el ángulo θ (según la regla de la mano derecha, en sentido contrario a las agujas del reloj en la figura).

Usando el producto escalar y el producto vectorial, el vector v se puede descomponer en componentes paralelos y perpendiculares al eje k, donde el componente paralelo a k es llamado vector proyección de v en k, y el componente perpendicular a k es llamado vector rechazo de v de k. El vector k × v se puede ver como una copia de v⊥ girada 90° en sentido antihorario alrededor de k, por lo que sus magnitudes son iguales pero las direcciones son perpendiculares.

Del mismo modo, el vector k × (k × v) es una copia de v⊥ girada 180° en sentido contrario a las agujas del reloj a través de k, de modo que k × (k × v) y v⊥ son iguales en magnitud pero en direcciones opuestas (es decir, son negativos entre sí, por lo tanto, de signos contrarios).

Al expandir el producto mixto se establece la conexión entre los componentes paralelo y perpendicular.

La fórmula resultante es a × (b × c) = (a · c)b − (a · b)c dado cualquiera de los tres vectores a, b, c. La componente paralela al eje no cambiará la magnitud ni la dirección bajo la rotación, solo la componente perpendicular cambiará de dirección pero conservará su magnitud, de acuerdo con y como k y v∥ son paralelos, su producto cruzado es cero k × v∥ = 0, por lo que y se sigue que Esta rotación es propia, ya que los vectores v⊥ y k × v tienen la misma longitud, y k × v es v⊥ girado 90° en sentido contrario a las agujas del reloj sobre k. Un escalado de v⊥ y k × v utilizando las funciones trigonométricas seno y coseno da el componente perpendicular girado.

La forma del componente girado es similar al desarrollo de un vector radial en el plano en coordenadas polares (r, θ) expresado en una base cartesiana 2D donde ex, ey son vectores unitarios en sus direcciones indicadas.

Ahora el vector rotado completo es Al sustituir las definiciones de v∥rot y v⊥rot en los resultados de la ecuación en Al representar v y k × v como matrices columna, el producto vectorial se puede expresar como una multiplicación de matrices Haciendo que K denote el "producto vectorial matricial" para el vector unitario k, La ecuación matricial es, simbólicamente, para cualquier vector v.

(De hecho, K es la matriz única con esta propiedad.

Iterar el producto cruzado a la derecha equivale a multiplicar por la matriz de productos cruzados a la izquierda, en particular Además, como k es un vector unitario, K se expresa en función de la unidad de la norma matricial.

La fórmula de rotación previa en lenguaje matricial es por lo tanto Téngase en cuenta que el coeficiente del término principal es ahora 1, en esta notación.

Factorizando v se obtiene la expresión compacta donde

es la matriz de rotación a través de un ángulo θ en sentido antihorario sobre el eje k, y I es la matriz identidad 3 × 3.

En términos de la matriz exponencial, Para ver que la última identidad se mantiene, se observa que característica de un grupo uniparamétrico, es decir, exponencial, y que las fórmulas coinciden con θ infinitesimal.