1 − 2 + 3 − 4 + ⋯

En matemáticas, la expresión 1 − 2 + 3 − 4 + ⋯ es una serie infinita cuyos términos son los números enteros, alternando signos.Sin embargo, a mediados del siglo XVIII, Leonardo Euler «demostró» la siguiente relación, calificándola de paradójica: No sería hasta mucho tiempo después que se lograría dar con una explicación rigurosa de dicha relación.Como base de los análisis en secciones subsiguientes, es útil analizar la divergencia en un nivel más fundamental.[2]​ Claramente no se aproxima ni converge a ningún número en particular, por lo tanto 1 − 2 + 3 − 4 + ⋯ diverge.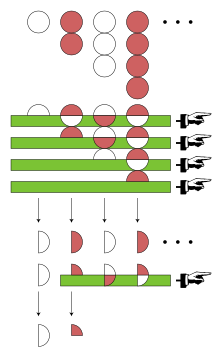Dado que los términos (1, −2, 3, −4, 5, −6…) siguen un patrón simple, se puede expresar a la serie 1 − 2 + 3 − 4 + ⋯ como una versión transformada de sí misma y resolver la ecuación resultante para obtener un valor numérico.Las manipulaciones mostradas previamente demuestran que: dado un método de sumación que es lineal y estable, si el mismo suma a la serie 1 − 2 + 3 − 4 + ⋯ entonces la suma debe ser 1⁄4, y ese método también permitirá sumar a la serie de Grandi 1 − 1 + 1 − 1 + · · · arrojando el valor 1⁄2.Si en cambio, se expresa la serie en una forma alternativa como un producto, entonces es posible determinar cuales son los métodos que permiten obtener 1⁄4.Dado que todas las formas del teorema de Cesàro son lineales y estables, las sumas resultan en los valores indicados previamente.Las sumas parciales son: y los promedios aritméticos de estas sumas parciales resultan ser: Dado que esta sucesión no converge, entonces se concluye que 1 − 2 + 3 − 4 + ⋯ no es sumable según el método de Cesàro.La «H» se usa en honor a Otto Hölder, quien fue el primero en demostrar en 1882 lo que hoy los matemáticos piensan es la conexión entre la sumación de Abel y la sumación (H, n); su primer ejemplo fue 1 − 2 + 3 − 4 + ⋯.[8]​ Leonhard Euler en un trabajo que escribe hacia 1749 admite que la serie diverge, pero de todas formas hace los aprontes para sumarla: En varias oportunidades Euler propuso una generalización de la palabra «suma».Comenzando desde el lado izquierdo, se puede seguir la heurística general indicada previamente y probar a multiplicar por (1+x) dos veces o elevar al cuadrado la serie geométrica 1 − x + x2 − · · ·.Para este último paso, la demostración correspondiente para 1 − 1 + 1 − 1 + · · · emplea el Teorema del valor medio, pero aquí se requiere la poderosa forma de Lagrange del teorema de Taylor.Eugène Charles Catalan, el maestro de Cesàro, también menospreciaba a las series divergentes.Finalmente, en su trabajo Sur la multiplication des series publicado en 1890, Cesàro adoptó un enfoque moderno comenzando desde las definiciones.