Número irracional

Número que no es un cociente de números enteros

El número √ 2 es irracional.

En matemáticas , los números irracionales ( in- + racionales ) son todos los números reales que no son números racionales . Es decir, los números irracionales no se pueden expresar como el cociente de dos números enteros . Cuando el cociente de longitudes de dos segmentos de línea es un número irracional, los segmentos de línea también se describen como inconmensurables , lo que significa que no comparten ninguna "medida" en común, es decir, no hay ninguna longitud ("la medida"), por corta que sea, que pueda usarse para expresar las longitudes de ambos segmentos dados como múltiplos enteros de sí mismos.

Entre los números irracionales se encuentran el cociente π entre la circunferencia de un círculo y su diámetro, el número de Euler e , la proporción áurea φ y la raíz cuadrada de dos . ^[1] De hecho, todas las raíces cuadradas de los números naturales , excepto de los cuadrados perfectos , son irracionales. ^[2]

Como todos los números reales, los números irracionales pueden expresarse en notación posicional , en particular como un número decimal. En el caso de los números irracionales, la expansión decimal no termina ni termina con una secuencia repetitiva . Por ejemplo, la representación decimal de π comienza con 3,14159, pero ningún número finito de dígitos puede representar π exactamente, ni se repite. Por el contrario, una expansión decimal que termina o se repite debe ser un número racional. Estas son propiedades demostrables de los números racionales y los sistemas de numeración posicional y no se utilizan como definiciones en matemáticas.

Los números irracionales también pueden expresarse como fracciones continuas no terminales (que en algunos casos son periódicas ) y de muchas otras maneras.

Como consecuencia de la prueba de Cantor de que los números reales son incontables y los racionales contables, se deduce que casi todos los números reales son irracionales. ^[3]

Historia

Diagrama de Euler que muestra el conjunto de números reales ( ), que incluyen los racionales ( ), que incluyen los enteros ( ), que incluyen los números naturales ( ). Los números reales también incluyen los irracionales ( \ ). ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {N} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$

Grecia antigua

La primera prueba de la existencia de los números irracionales se atribuye generalmente a un pitagórico (posiblemente Hípaso de Metaponto ), ^[4] que probablemente los descubrió al identificar los lados del pentagrama . ^[5] El método pitagórico habría afirmado que debe haber alguna unidad suficientemente pequeña e indivisible que pudiera caber de manera uniforme en una de estas longitudes, así como en la otra. Sin embargo, Hípaso en el siglo V a. C. fue capaz de deducir que no existía una unidad de medida común, y que la afirmación de tal existencia era una contradicción. Lo hizo demostrando que si la hipotenusa de un triángulo rectángulo isósceles era de hecho conmensurable con un cateto, entonces una de esas longitudes medidas en esa unidad de medida debe ser a la vez impar y par, lo cual es imposible. Su razonamiento es el siguiente:

• Comience con un triángulo rectángulo isósceles con lados de longitudes enteras a , b y c . La razón entre la hipotenusa y un cateto se representa mediante c : b .
• Supongamos que a , b y c están en los términos más pequeños posibles ( es decir, no tienen factores comunes).
• Por el teorema de Pitágoras : c ² = a ² + b ² = b ² + b ² = 2 b ² . (Como el triángulo es isósceles, a = b ).
• Como c ² = 2 b ² , c ² es divisible por 2 y, por lo tanto, par.
• Como c ² es par, c debe ser par.
• Como c es par, al dividir c por 2 obtenemos un entero. Sea y este entero ( c = 2 y ).
• Elevando al cuadrado ambos lados de c = 2 y se obtiene c ² = (2 y ) ² , o c ² = 4 y ² .
• Sustituyendo 4 y ² por c ² en la primera ecuación ( c ² = 2 b ² ) obtenemos 4 y ² = 2 b ² .
• Dividiendo por 2 obtenemos 2 y ² = b ² .
• Como y es un número entero y 2 y ² = b ² , b ² es divisible por 2 y, por lo tanto, par.
• Como b ² es par, b debe ser par.
• Acabamos de demostrar que tanto b como c deben ser pares. Por lo tanto, tienen un factor común de 2. Sin embargo, esto contradice la suposición de que no tienen factores comunes. Esta contradicción prueba que c y b no pueden ser ambos números enteros y, por lo tanto, la existencia de un número que no se puede expresar como cociente de dos números enteros. ^[6]

Los matemáticos griegos denominaron a esta relación de magnitudes inconmensurables álogos , o inexpresable. Sin embargo, Hípaso no fue elogiado por sus esfuerzos: según una leyenda, hizo su descubrimiento mientras estaba en el mar, y posteriormente fue arrojado por la borda por sus compañeros pitagóricos "por haber producido un elemento en el universo que negaba la... doctrina de que todos los fenómenos del universo pueden reducirse a números enteros y sus proporciones". ^[7] Otra leyenda afirma que Hípaso fue simplemente exiliado por esta revelación. Cualquiera que sea la consecuencia para el propio Hípaso, su descubrimiento planteó un problema muy serio para las matemáticas pitagóricas, ya que hizo añicos la suposición de que los números y la geometría eran inseparables, un fundamento de su teoría.

El descubrimiento de razones inconmensurables fue indicativo de otro problema al que se enfrentaban los griegos: la relación entre lo discreto y lo continuo. Esto fue sacado a la luz por Zenón de Elea , quien cuestionó la concepción de que las cantidades son discretas y compuestas de un número finito de unidades de un tamaño dado. Las concepciones griegas anteriores dictaban que necesariamente debían serlo, ya que "los números enteros representan objetos discretos, y una razón conmensurable representa una relación entre dos conjuntos de objetos discretos", ^[8] pero Zenón descubrió que, de hecho, "[las cantidades] en general no son conjuntos discretos de unidades; es por eso que aparecen razones de [cantidades] inconmensurables... [L]as cantidades son, en otras palabras, continuas". ^[8] Lo que esto significa es que, contrariamente a la concepción popular de la época, no puede haber una unidad de medida indivisible, la más pequeña, para ninguna cantidad. De hecho, estas divisiones de cantidad deben ser necesariamente infinitas . Por ejemplo, consideremos un segmento de línea: este segmento puede dividirse en dos, esa mitad dividirse en dos, la mitad de la mitad en dos, y así sucesivamente. Este proceso puede continuar infinitamente, ya que siempre hay otra mitad que dividir. Cuanto más veces se divide el segmento en dos, más se acerca la unidad de medida a cero, pero nunca llega exactamente a cero. Esto es precisamente lo que Zenón trató de demostrar. Trató de demostrarlo formulando cuatro paradojas , que demostraban las contradicciones inherentes al pensamiento matemático de la época. Si bien las paradojas de Zenón demostraron con precisión las deficiencias de las concepciones matemáticas contemporáneas, no se las consideró una prueba de la alternativa. En la mente de los griegos, refutar la validez de una visión no necesariamente demostraba la validez de otra y, por lo tanto, tenía que realizarse una investigación más profunda.

El siguiente paso lo dio Eudoxo de Cnido , quien formalizó una nueva teoría de la proporción que tenía en cuenta las cantidades conmensurables y las inconmensurables. En el centro de su idea estaba la distinción entre magnitud y número. Una magnitud "... no era un número sino que representaba entidades como segmentos de línea, ángulos, áreas, volúmenes y tiempo que podían variar, como diríamos, de forma continua. Las magnitudes se oponían a los números, que saltaban de un valor a otro, como de 4 a 5". ^[9] Los números se componen de una unidad mínima e indivisible, mientras que las magnitudes son infinitamente reducibles. Como no se asignaban valores cuantitativos a las magnitudes, Eudoxo pudo explicar tanto las razones conmensurables como las inconmensurables definiendo una razón en términos de su magnitud y la proporción como una igualdad entre dos razones. Al sacar los valores cuantitativos (números) de la ecuación, evitó la trampa de tener que expresar un número irracional como un número. "La teoría de Eudoxo permitió a los matemáticos griegos realizar enormes avances en geometría al proporcionar la base lógica necesaria para las razones inconmensurables". ^[10] Esta inconmensurabilidad se aborda en los Elementos de Euclides, Libro X, Proposición 9. No fue hasta que Eudoxo desarrolló una teoría de la proporción que tenía en cuenta las razones irracionales y racionales que se creó una base matemática sólida de los números irracionales. ^[11]

Como resultado de la distinción entre número y magnitud, la geometría se convirtió en el único método que podía tener en cuenta proporciones inconmensurables. Debido a que los fundamentos numéricos anteriores todavía eran incompatibles con el concepto de inconmensurabilidad, el enfoque griego se alejó de concepciones numéricas como el álgebra y se concentró casi exclusivamente en la geometría. De hecho, en muchos casos, las concepciones algebraicas se reformularon en términos geométricos. Esto puede explicar por qué todavía concebimos x ² y x ³ como x al cuadrado y x al cubo en lugar de x a la segunda potencia y x a la tercera potencia. También fue crucial para el trabajo de Zenón con magnitudes inconmensurables el enfoque fundamental en el razonamiento deductivo que resultó de la ruptura de los fundamentos de las matemáticas griegas anteriores. La comprensión de que alguna concepción básica dentro de la teoría existente estaba en desacuerdo con la realidad requirió una investigación completa y exhaustiva de los axiomas y supuestos que sustentan esa teoría. A partir de esta necesidad, Eudoxo desarrolló su método de agotamiento , una especie de reductio ad absurdum que "...estableció la organización deductiva sobre la base de axiomas explícitos..." así como "...reforzó la decisión anterior de confiar en el razonamiento deductivo para la prueba". ^[12] Este método de agotamiento es el primer paso en la creación del cálculo.

Teodoro de Cirene demostró la irracionalidad de los radicales de los números enteros hasta el 17, pero se detuvo allí probablemente porque el álgebra que utilizó no podía aplicarse a la raíz cuadrada de 17. ^[13]

India

Los problemas geométricos y matemáticos que involucran números irracionales, como las raíces cuadradas, se abordaron muy temprano durante el período védico en la India. Existen referencias a tales cálculos en los Samhitas , los Brahmanas y los Shulba Sutras (800 a. C. o antes). ^[14]

Se sugiere que el concepto de irracionalidad fue aceptado implícitamente por los matemáticos indios desde el siglo VII a. C., cuando Manava (c. 750 – 690 a. C.) creía que las raíces cuadradas de números como 2 y 61 no podían determinarse con exactitud. ^[15] El historiador Carl Benjamin Boyer , sin embargo, escribe que "tales afirmaciones no están bien fundamentadas y es poco probable que sean ciertas". ^[16]

Más tarde, en sus tratados, los matemáticos indios escribieron sobre la aritmética de los números irracionales, incluyendo la suma, la resta, la multiplicación, la racionalización, así como la separación y extracción de raíces cuadradas. ^[17]

Matemáticos como Brahmagupta (en el año 628 d. C.) y Bhāskara I (en el año 629 d. C.) hicieron contribuciones en esta área, al igual que otros matemáticos que los siguieron. En el siglo XII, Bhāskara II evaluó algunas de estas fórmulas y las criticó, identificando sus limitaciones.

Durante los siglos XIV al XVI, Madhava de Sangamagrama y la escuela de astronomía y matemáticas de Kerala descubrieron la serie infinita de varios números irracionales como π y ciertos valores irracionales de funciones trigonométricas . Jyeṣṭhadeva proporcionó pruebas de estas series infinitas en el Yuktibhāṣā . ^[18]

Mundo islámico

En la Edad Media , el desarrollo del álgebra por parte de los matemáticos musulmanes permitió que los números irracionales fueran tratados como objetos algebraicos . ^[19] Los matemáticos de Oriente Medio también fusionaron los conceptos de « número » y « magnitud » en una idea más general de los números reales , criticaron la idea de Euclides de las proporciones , desarrollaron la teoría de las proporciones compuestas y extendieron el concepto de número a las proporciones de magnitud continua. ^[20] En su comentario al Libro 10 de los Elementos , el matemático persa Al-Mahani (fallecido en 874/884) examinó y clasificó los irracionales cuadráticos y los irracionales cúbicos. Proporcionó definiciones para las magnitudes racionales e irracionales, que trató como números irracionales. Las trató con libertad, pero las explicó en términos geométricos de la siguiente manera: ^[20]

"Será una magnitud racional cuando digamos, por ejemplo, 10, 12, 3%, 6%, etc., porque su valor se pronuncia y se expresa cuantitativamente. Lo que no es racional es irracional y es imposible pronunciar y representar cuantitativamente su valor. Por ejemplo: las raíces de números como 10, 15, 20 que no son cuadrados, los lados de números que no son cubos, etc. "

En contraste con el concepto euclidiano de magnitudes como líneas, Al-Mahani consideró los números enteros y las fracciones como magnitudes racionales, y las raíces cuadradas y cúbicas como magnitudes irracionales. También introdujo un enfoque aritmético del concepto de irracionalidad, ya que atribuye a las magnitudes irracionales lo siguiente: ^[20]

"sus sumas o diferencias, o resultados de su adición a una magnitud racional, o resultados de restar una magnitud de esta clase de una irracional, o de una magnitud racional de ella."

El matemático egipcio Abū Kāmil Shujā ibn Aslam (c. 850 – 930) fue el primero en aceptar números irracionales como soluciones a ecuaciones cuadráticas o como coeficientes en una ecuación en forma de raíces cuadradas y raíces cuartas . ^[21] En el siglo X, el matemático iraquí Al-Hashimi proporcionó pruebas generales (en lugar de demostraciones geométricas) para los números irracionales, ya que consideró la multiplicación, la división y otras funciones aritméticas. ^[20]

Muchos de estos conceptos fueron finalmente aceptados por los matemáticos europeos en algún momento después de las traducciones latinas del siglo XII . Al-Hassār , un matemático marroquí de Fez especializado en jurisprudencia islámica sobre herencia durante el siglo XII, menciona por primera vez el uso de una barra fraccionaria, donde los numeradores y denominadores están separados por una barra horizontal. En su discusión, escribe: "..., por ejemplo, si se le dice que escriba tres quintos y un tercio de un quinto, escriba así, ." ^[22] Esta misma notación fraccionaria aparece poco después en la obra de Leonardo Fibonacci en el siglo XIII. ^[23] ${\displaystyle {\frac {3\quad 1}{5\quad 3}}}$

Periodo moderno

El siglo XVII vio a los números imaginarios convertirse en una poderosa herramienta en manos de Abraham de Moivre , y especialmente de Leonhard Euler . La finalización de la teoría de los números complejos en el siglo XIX implicó la diferenciación de los irracionales en números algebraicos y trascendentales , la prueba de la existencia de los números trascendentales y el resurgimiento del estudio científico de la teoría de los irracionales, en gran parte ignorada desde Euclides . El año 1872 vio la publicación de las teorías de Karl Weierstrass (por su alumno Ernst Kossak), Eduard Heine ( Diario de Crelle , 74), Georg Cantor (Annalen, 5) y Richard Dedekind . Méray había tomado en 1869 el mismo punto de partida que Heine, pero la teoría se refiere generalmente al año 1872. El método de Weierstrass ha sido completamente expuesto por Salvatore Pincherle en 1880, ^[24] y el de Dedekind ha recibido prominencia adicional a través del trabajo posterior del autor (1888) y el respaldo de Paul Tannery (1894). Weierstrass, Cantor y Heine basan sus teorías en series infinitas, mientras que Dedekind funda la suya en la idea de un corte (Schnitt) en el sistema de todos los números racionales , separándolos en dos grupos que tienen ciertas propiedades características. El tema ha recibido contribuciones posteriores de manos de Weierstrass, Leopold Kronecker (Crelle, 101) y Charles Méray .

Las fracciones continuas , estrechamente relacionadas con los números irracionales (y debidas a Cataldi, 1613), recibieron atención de manos de Euler y, a principios del siglo XIX, adquirieron prominencia gracias a los escritos de Joseph-Louis Lagrange . Dirichlet también contribuyó a la teoría general, al igual que numerosos contribuyentes a las aplicaciones del tema.

Johann Heinrich Lambert demostró (1761) que π no puede ser racional, y que e ⁿ es irracional si n es racional (a menos que n  = 0). ^[25] Aunque la prueba de Lambert suele calificarse de incompleta, las evaluaciones modernas la sostienen como satisfactoria y, de hecho, para su época es inusualmente rigurosa. Adrien-Marie Legendre (1794), después de introducir la función de Bessel-Clifford , proporcionó una prueba para demostrar que π ² es irracional, de donde se sigue inmediatamente que π también es irracional. La existencia de números trascendentales fue establecida por primera vez por Liouville (1844, 1851). Más tarde, Georg Cantor (1873) demostró su existencia mediante un método diferente , que mostró que cada intervalo en los números reales contiene números trascendentales. Charles Hermite (1873) fue el primero en demostrar que e es trascendental, y Ferdinand von Lindemann (1882), partiendo de las conclusiones de Hermite, demostró lo mismo para π. La prueba de Lindemann fue simplificada en gran medida por Weierstrass (1885), y más aún por David Hilbert (1893), y finalmente fue simplificada por Adolf Hurwitz ^{[ cita requerida ]} y Paul Gordan . ^[26]

Ejemplos

Raíces cuadradas

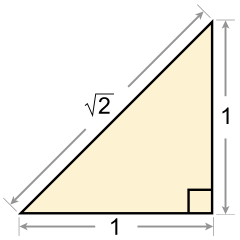
La raíz cuadrada de 2 fue probablemente el primer número que se demostró que era irracional. ^[27] La ​​proporción áurea es otro famoso número irracional cuadrático. Las raíces cuadradas de todos los números naturales que no son cuadrados perfectos son irracionales y se puede encontrar una prueba en los irracionales cuadráticos .

Raíces generales

La prueba de la irracionalidad de la raíz cuadrada de dos se puede generalizar utilizando el teorema fundamental de la aritmética . Este afirma que cada número entero tiene una única factorización en primos. Con él podemos demostrar que si un número racional no es un número entero, entonces ninguna potencia entera de él puede ser un número entero, ya que en términos mínimos debe haber un primo en el denominador que no divida al numerador, sea cual sea la potencia a la que se eleve cada uno. Por lo tanto, si un número entero no es una k -ésima potencia exacta de otro número entero, entonces la k -ésima raíz de ese primer número entero es irracional.

Logaritmos

Tal vez los números más fáciles de demostrar como irracionales sean ciertos logaritmos . He aquí una prueba por contradicción de que log ₂  3 es irracional (log ₂  3 ≈ 1,58 > 0).

Supongamos que log ₂  3 es racional. Para algunos números enteros positivos m y n , tenemos

${\displaystyle \log _{2}3={\frac {m}{n}}.}$

Resulta que

${\displaystyle 2^{m/n}=3}$

${\displaystyle (2^{m/n})^{n}=3^{n}}$

${\displaystyle 2^{m}=3^{n}.}$

El número 2 elevado a cualquier potencia entera positiva debe ser par (porque es divisible por 2) y el número 3 elevado a cualquier potencia entera positiva debe ser impar (porque ninguno de sus factores primos será 2). Claramente, un número entero no puede ser par e impar al mismo tiempo: tenemos una contradicción. La única suposición que hicimos fue que log ₂  3 es racional (y por lo tanto expresable como un cociente de números enteros m / n con n  ≠ 0). La contradicción significa que esta suposición debe ser falsa, es decir, log ₂  3 es irracional y nunca puede expresarse como un cociente de números enteros m / n con n  ≠ 0.

Casos como el de log ₁₀  2 pueden tratarse de manera similar.

Tipos

Un número irracional puede ser algebraico , es decir raíz real de un polinomio con coeficientes enteros. Los que no son algebraicos son trascendentales .

Algebraico

Los números algebraicos reales son las soluciones reales de las ecuaciones polinómicas.

${\displaystyle p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0\;,}$

donde los coeficientes son números enteros y . Un ejemplo de un número algebraico irracional es x ₀  = (2 ^1/2  + 1) ^1/3 . Es claramente algebraico ya que es la raíz de un polinomio entero, , que es equivalente a . Este polinomio no tiene raíces racionales, ya que el teorema de la raíz racional muestra que las únicas posibilidades son ±1, pero x ₀ es mayor que 1. Por lo tanto , x ₀ es un número algebraico irracional. Hay una cantidad contable de números algebraicos, ya que hay una cantidad contable de polinomios enteros. ${\displaystyle a_{i}}$ ${\displaystyle a_{n}\neq 0}$ ${\displaystyle (x^{3}-1)^{2}=2}$ ${\displaystyle (x^{6}-2x^{3}-1)=0}$

Trascendental

Casi todos los números irracionales son trascendentales . Algunos ejemplos son e ^r y π ^r , que son trascendentales para todos los números racionales  r distintos de cero.  

Como los números algebraicos forman un subcuerpo de los números reales, muchos números reales irracionales pueden construirse combinando números trascendentales y algebraicos. Por ejemplo, 3 π  + 2, π  +  √ 2 y e √ 3 son irracionales (e incluso trascendentales).

Expansiones decimales

La expansión decimal de un número irracional nunca se repite (es decir, la expansión decimal no repite el mismo número o secuencia de números) ni termina (esto significa que no hay un número finito de dígitos distintos de cero), a diferencia de cualquier número racional. Lo mismo es válido para las expansiones binarias , octales o hexadecimales y, en general, para las expansiones en toda notación posicional con bases naturales .

Para demostrarlo, supongamos que dividimos números enteros n por m (donde m es distinto de cero). Cuando se aplica una división larga a la división de n por m , nunca puede haber un resto mayor o igual a m . Si aparece 0 como resto, la expansión decimal termina. Si nunca aparece 0, entonces el algoritmo puede ejecutarse como máximo m − 1 pasos sin utilizar ningún resto más de una vez. Después de eso, debe recurrirse a un resto y luego se repite la expansión decimal.

Por el contrario, supongamos que nos encontramos ante un decimal periódico , podemos demostrar que es una fracción de dos números enteros. Por ejemplo, consideremos:

${\displaystyle A=0.7\,162\,162\,162\,\ldots }$

Aquí, el número de repetición es 162 y su longitud es 3. Primero, multiplicamos por una potencia de 10 adecuada para mover el punto decimal hacia la derecha de modo que quede justo delante de un número de repetición. En este ejemplo, multiplicaríamos por 10 para obtener:

${\displaystyle 10A=7.162\,162\,162\,\ldots }$

Ahora multiplicamos esta ecuación por 10 ^r , donde r es la longitud de la repetición. Esto tiene el efecto de mover el punto decimal para que quede delante de la repetición "próxima". En nuestro ejemplo, multiplicamos por 10 ³ :

${\displaystyle 10,000A=7\,162.162\,162\,\ldots }$

El resultado de las dos multiplicaciones da dos expresiones diferentes con exactamente la misma "porción decimal", es decir, el extremo final de 10 000 A coincide exactamente con el extremo final de 10 A. Aquí, tanto 10 000 A como 10 A tienen 0,162 162 162 ... después del punto decimal.

Por lo tanto, cuando restamos la ecuación de 10 A de la ecuación de 10 000 A , el extremo final de 10 A cancela el extremo final de 10 000 A, dejándonos con:

${\displaystyle 9990A=7155.}$

Entonces

${\displaystyle A={\frac {7155}{9990}}={\frac {53}{74}}}$

es un cociente de números enteros y por tanto un número racional.

Poderes irracionales

Dov Jarden dio una prueba simple y no constructiva de que existen dos números irracionales a y b , tales que a ^b es racional: ^{[28] [29]}

Considere √ 2 ^{√ 2} ; si es racional, entonces tome a = b = √ 2 . De lo contrario, tome a como el número irracional √ 2 ^{√ 2} y b = √ 2 . Entonces a ^b = ( √ 2 ^{√ 2} ) ^{√ 2} = √ 2 ^{√ 2 · √ 2} = √ 2 ² = 2, que es racional.

Aunque el argumento anterior no decide entre los dos casos, el teorema de Gelfond-Schneider muestra que √ 2 ^{√ 2} es trascendental , por lo tanto irracional. Este teorema establece que si a y b son ambos números algebraicos , y a no es igual a 0 o 1, y b no es un número racional, entonces cualquier valor de a ^b es un número trascendental (puede haber más de un valor si se utiliza la exponenciación de números complejos ).

Un ejemplo que proporciona una prueba constructiva simple es ^[30]

${\displaystyle \left({\sqrt {2}}\right)^{\log _{\sqrt {2}}3}=3.}$

La base del lado izquierdo es irracional y la del lado derecho es racional, por lo que hay que demostrar que el exponente del lado izquierdo, , es irracional. Esto es así porque, por la fórmula que relaciona logaritmos con bases diferentes, ${\displaystyle \log _{\sqrt {2}}3}$

${\displaystyle \log _{\sqrt {2}}3={\frac {\log _{2}3}{\log _{2}{\sqrt {2}}}}={\frac {\log _{2}3}{1/2}}=2\log _{2}3}$

que podemos suponer, con el fin de establecer una contradicción , que es igual a una razón m/n de números enteros positivos. Entonces, de ahí de ahí de ahí , que es un par contradictorio de factorizaciones primas y, por lo tanto, viola el teorema fundamental de la aritmética (factorización prima única). ${\displaystyle \log _{2}3=m/2n}$ ${\displaystyle 2^{\log _{2}3}=2^{m/2n}}$ ${\displaystyle 3=2^{m/2n}}$ ${\displaystyle 3^{2n}=2^{m}}$

Un resultado más contundente es el siguiente: ^{[ 31]} Todo número racional en el intervalo puede escribirse como a para algún número irracional a o como n ⁿ para algún número natural n . De manera similar, ^[31] todo número racional positivo puede escribirse como para algún número irracional a o como para algún número natural n . ${\displaystyle ((1/e)^{1/e},\infty )}$ ${\displaystyle a^{a^{a}}}$ ${\displaystyle n^{n^{n}}}$

Preguntas abiertas

No se sabe si (o ) es irracional. De hecho, no hay ningún par de números enteros distintos de cero para los que se sepa si es irracional. Además, no se sabe si el conjunto es algebraicamente independiente en . ${\displaystyle \pi +e}$ ${\displaystyle \pi -e}$ ${\displaystyle m,n}$ ${\displaystyle m\pi +ne}$ ${\displaystyle \{\pi ,e\}}$ ${\displaystyle \mathbb {Q} }$

No se sabe si la constante de Catalan o la constante de Euler-Mascheroni son irracionales. ^[32] No se sabe si alguna de las tetraciones o es racional para algún número entero ^{[ cita requerida ]} ${\displaystyle \pi e,\ \pi /e,\ \pi ^{e},\ \pi ^{\sqrt {2}},\ \ln \pi ,}$ ${\displaystyle \gamma }$ ${\displaystyle ^{n}\pi }$ ${\displaystyle ^{n}e}$ ${\displaystyle n>1.}$

En matemáticas constructivas

En matemáticas constructivas , el tercero excluido no es válido, por lo que no es cierto que todo número real sea racional o irracional. Por lo tanto, la noción de número irracional se bifurca en múltiples nociones distintas. Se podría tomar la definición tradicional de un número irracional como un número real que no es racional. ^[33] Sin embargo, hay una segunda definición de un número irracional utilizada en matemáticas constructivas, que un número real es un número irracional si está separado de todo número racional, o equivalentemente, si la distancia entre y todo número racional es positiva. Esta definición es más fuerte que la definición tradicional de un número irracional. Esta segunda definición se utiliza en la prueba de Errett Bishop de que la raíz cuadrada de 2 es irracional . ^[34] ${\displaystyle r}$ ${\displaystyle \vert r-q\vert }$ ${\displaystyle r}$ ${\displaystyle q}$

Conjunto de todos los irracionales

Como los reales forman un conjunto incontable , del cual los racionales son un subconjunto contable , el conjunto complementario de los irracionales es incontable.

Bajo la función de distancia ( euclidiana ) usual , los números reales son un espacio métrico y por lo tanto también un espacio topológico . Restringiendo la función de distancia euclidiana se da a los irracionales la estructura de un espacio métrico. Puesto que el subespacio de los irracionales no es cerrado, la métrica inducida no es completa . Al ser un conjunto G-delta —es decir, una intersección contable de subconjuntos abiertos— en un espacio métrico completo, el espacio de los irracionales es completamente metrizable : es decir, hay una métrica sobre los irracionales que induce la misma topología que la restricción de la métrica euclidiana, pero con respecto a la cual los irracionales son completos. Uno puede ver esto sin conocer el hecho antes mencionado sobre los conjuntos G-delta: la expansión fraccionaria continua de un número irracional define un homeomorfismo desde el espacio de los irracionales al espacio de todas las sucesiones de números enteros positivos, que se ve fácilmente que es completamente metrizable. ${\displaystyle d(x,y)=\vert x-y\vert }$

Además, el conjunto de todos los irracionales es un espacio metrizable desconectado. De hecho, los irracionales dotados de la topología de subespacio tienen una base de grupos clopen, por lo que el espacio es de dimensión cero .

Véase también

• Número de Brjuno
• Número computable
• Aproximación diofántica
• Medida de irracionalidad
• Prueba de que e es irracional
• Prueba de que π es irracional
• Raíz cuadrada de 3
• Raíz cuadrada de 5
• Número trigonométrico

Referencias

1. Los 15 números trascendentales más famosos. por Clifford A. Pickover . URL recuperada el 24 de octubre de 2007.
2. Jackson, Terence (1 de julio de 2011). "95.42 Raíces cuadradas irracionales de números naturales: un enfoque geométrico". The Mathematical Gazette . 95 (533): 327–330. doi :10.1017/S0025557200003193. ISSN  0025-5572. S2CID  123995083.
3. Cantor, Georg (1955) [1915]. Philip Jourdain (ed.). Contribuciones a la fundación de la teoría de los números transfinitos. Nueva York: Dover. ISBN 978-0-486-60045-1.
4. Kurt Von Fritz (1945). "El descubrimiento de la inconmensurabilidad por Hípaso de Metaponto". Anales de Matemáticas . 46 (2): 242–264. doi :10.2307/1969021. JSTOR  1969021. S2CID  126296119.
5. James R. Choike (1980). "El pentagrama y el descubrimiento de un número irracional". The Two-Year College Mathematics Journal . 11 (5): 312–316. doi :10.2307/3026893. JSTOR  3026893. S2CID  115390951.
6. Kline, M. (1990). Mathematical Thought from Ancient to Modern Times , vol. 1. Nueva York: Oxford University Press (obra original publicada en 1972), pág. 33.
7. Kline 1990, pág. 32.
8. Kline 1990, pág. 34.
9. Kline 1990, pág. 48.
10. Kline 1990, pág. 49.
11. Charles H. Edwards (1982). El desarrollo histórico del cálculo . Springer.
12. Kline 1990, pág. 50.
13. Robert L. McCabe (1976). "Las pruebas de irracionalidad de Teodoro". Revista de Matemáticas . 49 (4): 201–203. doi :10.1080/0025570X.1976.11976579. JSTOR  2690123. S2CID  124565880..
14. Bag, Amulya Kumar (1990). "Geometría ritual en la India y su paralelismo en otras áreas culturales". Revista india de historia de la ciencia . 25 .
15. TK Puttaswamy, "Los logros de los antiguos matemáticos indios", págs. 411-2, en Selin, Helaine ; D'Ambrosio, Ubiratan, eds. (2000). Matemáticas en todas las culturas: la historia de las matemáticas no occidentales . Springer . ISBN 1-4020-0260-2..
16. Boyer (1991). "China y la India". Una historia de las matemáticas (2.ª ed.). Wiley. pág. 208. ISBN 0471093742. OCLC  414892. También se ha afirmado que el primer reconocimiento de magnitudes inconmensurables aparece en la India durante el período Sulbasutra , pero tales afirmaciones no están bien fundamentadas. La falta de pruebas de que los matemáticos indios de ese período hubieran llegado a comprender conceptos fundamentales hace que la idea de que los primeros hindúes tuvieran conciencia de las magnitudes inconmensurables sea muy poco probable.
17. Datta, Bibhutibhusan; Singh, Awadhesh Narayan (1993). "Surds in Hindu mathematics" (PDF) . Indian Journal of History of Science . 28 (3): 253–264. Archivado desde el original (PDF) el 2018-10-03 . Consultado el 18 de septiembre de 2018 .
18. Katz, VJ (1995). "Ideas de cálculo en el Islam y la India". Revista de matemáticas . 63 (3): 163–174. doi :10.2307/2691411. JSTOR  2691411.
19. O'Connor, John J.; Robertson, Edmund F. (1999). "Matemáticas árabes: ¿brillantez olvidada?". Archivo de Historia de las Matemáticas de MacTutor . Universidad de St Andrews ..
20. Matvievskaya, Galina (1987). "La teoría de los irracionales cuadráticos en las matemáticas medievales orientales". Anales de la Academia de Ciencias de Nueva York . 500 (1): 253–277. Bibcode :1987NYASA.500..253M. doi :10.1111/j.1749-6632.1987.tb37206.x. S2CID  121416910.Véanse en particular las páginas 254 y 259-260.
21. Jacques Sesiano, "Matemáticas islámicas", p. 148, en Selin, Helaine; D'Ambrosio, Ubiratan (2000). Matemáticas entre culturas: la historia de las matemáticas no occidentales . Saltador . ISBN 1-4020-0260-2..
22. Cajori, Florian (1928). Una historia de las notaciones matemáticas (Vol. 1) . La Salle, Illinois: The Open Court Publishing Company.pág. 269.
23. (Cajori 1928, pág. 89)
24. Salvatore Pincherle (1880). "Saggio di una introduzione alla teoria delle funzioni analitiche secondo i principii del prof. C. Weierstrass". Giornale di Matematiche : 178–254, 317–320.
25. Lambert, JH (1761). "Mémoire sur quelques propriétés remarquables des quantités trascendentes, circulaires et logarithmiques" (PDF) . Mémoires de l'Académie royale des sciences de Berlin (en francés): 265–322. Archivado (PDF) desde el original el 28 de abril de 2016.
26. Gordon, Paul (1893). "Trascendenz von e und π". Annalen Matemáticas . 43 (2-3). Teubner: 222-224. doi :10.1007/bf01443647. S2CID  123203471.
27. Fowler, David H. (2001), "La historia del descubrimiento de la inconmensurabilidad, revisada", Neusis (10): 45–61, MR  1891736
28. Jarden, Dov (1953). "Curiosa No. 339: Una prueba simple de que una potencia de un número irracional elevada a un exponente irracional puede ser racional". Scripta Mathematica . 19 : 229.Copiar
29. Jorge, Alejandro; Velleman, Daniel J. (2002). Filosofías de las matemáticas (PDF) . Blackwell. págs. 3–4. ISBN 0-631-19544-0.
30. Lord, Nick, "Las matemáticas muerden: las potencias irracionales de los números irracionales pueden ser racionales", Mathematical Gazette 92, noviembre de 2008, pág. 534.
31. Marshall, Ash J., y Tan, Yiren, "Un número racional de la forma a ^a con un irracional", Mathematical Gazette 96, marzo de 2012, págs. 106-109.
32. Albert, John. "Algunos problemas no resueltos en teoría de números" (PDF) . Departamento de Matemáticas, Universidad de Oklahoma.(Seminario de Matemáticas para estudiantes avanzados, curso de primavera de 2008)
33. Mark Bridger (2007). Análisis real: un enfoque constructivo a través de la aritmética de intervalos . John Wiley & Sons . ISBN 978-1-470-45144-8.
34. Errett Bishop; Douglas Bridges (1985). Análisis constructivo . Springer . ISBN 0-387-15066-8.

Lectura adicional

• Adrien-Marie Legendre , Éléments de Géometrie , Nota IV, (1802), París
• Rolf Wallisser, "Sobre la prueba de Lambert de la irracionalidad de π", en Teoría algebraica de números y análisis diofántico , Franz Halter-Koch y Robert F. Tichy, (2000), Walter de Gruyter

Enlaces externos

• Las paradojas y la inconmensurabilidad de Zenón Archivado el 13 de mayo de 2016 en Wayback Machine (sin fecha). Consultado el 1 de abril de 2008