partición entera

Descomposición de un número entero como suma de números enteros positivos

Diagramas de Young asociados a las particiones de los números enteros positivos del 1 al 8. Están dispuestos de manera que las imágenes bajo la reflexión sobre la diagonal principal del cuadrado sean particiones conjugadas.

Particiones de n con mayor parte k

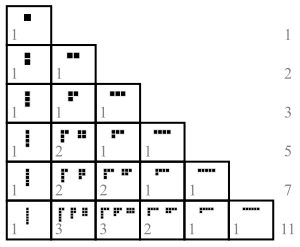
En teoría de números y combinatoria , una partición de un número entero no negativo n , también llamada partición entera , es una forma de escribir n como una suma de números enteros positivos . Dos sumas que difieren sólo en el orden de sus sumandos se consideran la misma partición. (Si el orden importa, la suma se convierte en una composición ). Por ejemplo, 4 se puede dividir de cinco maneras distintas:

4

3 + 1

2 + 2

2+1+1

1+1+1+1

La única partición del cero es la suma vacía, sin partes.

La composición dependiente del orden 1 + 3 es la misma partición que 3 + 1 , y las dos composiciones distintas 1 + 2 + 1 y 1 + 1 + 2 representan la misma partición que 2 + 1 + 1 .

Un sumando individual en una partición se llama parte . El número de particiones de n viene dado por la función de partición p ( n ) . Entonces p (4) = 5 . La notación λ ⊢ n significa que λ es una partición de n .

Las particiones se pueden visualizar gráficamente con diagramas de Young o diagramas de Ferrers . Ocurren en varias ramas de las matemáticas y la física , incluido el estudio de polinomios simétricos y del grupo simétrico y en la teoría de representación de grupos en general.

Ejemplos

Las siete particiones de 5 son

• 5
• 4 + 1
• 3 + 2
• 3+1+1
• 2 + 2 + 1
• 2+1+1+1
• 1+1+1+1+1

Algunos autores tratan una partición como una secuencia decreciente de sumandos, en lugar de una expresión con signos más. Por ejemplo, la partición 2 + 2 + 1 podría escribirse como la tupla (2, 2, 1) o en la forma aún más compacta (2 ² , 1) donde el superíndice indica el número de repeticiones de una parte.

Esta notación de multiplicidad para una partición se puede escribir alternativamente como , donde m ₁ es el número de 1, m ₂ es el número de 2, etc. (Se pueden omitir los componentes con m _i = 0 ). Por ejemplo, en esta notación, se escriben las particiones de 5 , y . ${\displaystyle 1^{m_{1}}2^{m_{2}}3^{m_{3}}\cdots }$ ${\displaystyle 5^{1},1^{1}4^{1},2^{1}3^{1},1^{2}3^{1},1^{1}2^{2},1^{3}2^{1}}$ ${\displaystyle 1^{5}}$

Representaciones esquemáticas de particiones.

Hay dos métodos esquemáticos comunes para representar particiones: como diagramas de Ferrers, llamados así en honor a Norman Macleod Ferrers , y como diagramas de Young, llamados así en honor a Alfred Young . Ambos tienen varias convenciones posibles; aquí usamos notación inglesa , con diagramas alineados en la esquina superior izquierda.

Diagrama de Ferrer

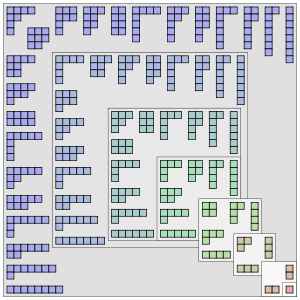
La partición 6 + 4 + 3 + 1 del número 14 se puede representar mediante el siguiente diagrama:

Los 14 círculos están alineados en 4 filas, cada una del tamaño de una parte de la partición. Los diagramas para las 5 particiones del número 4 se muestran a continuación:

diagrama joven

Una representación visual alternativa de una partición entera es su diagrama de Young (a menudo también llamado diagrama de Ferrers). En lugar de representar una partición con puntos, como en el diagrama de Ferrers, el diagrama de Young utiliza cuadros o cuadrados. Por tanto, el diagrama de Young para la partición 5 + 4 + 1 es

mientras que el diagrama de Ferrers para la misma partición es

Si bien esta variación aparentemente trivial no parece digna de mención separada, los diagramas de Young resultan extremadamente útiles en el estudio de las funciones simétricas y la teoría de la representación de grupos : llenar las cajas de los diagramas de Young con números (o, a veces, objetos más complicados) que obedecen a varias reglas. conduce a una familia de objetos llamados cuadros jóvenes , y estos cuadros tienen un significado combinatorio y teórico de la representación. ^[1] Como un tipo de forma formada por cuadrados adyacentes unidos, los diagramas de Young son un tipo especial de poliominó . ^[2]

Función de partición

Usando el método de Euler para encontrar p (40): se desliza hacia abajo una regla con signos más y menos (cuadro gris), y se suman o restan las partes relevantes. Las posiciones de los signos vienen dadas por las diferencias de alternancia de números naturales (azul) e impares (naranja). En el archivo SVG, coloque el cursor sobre la imagen para mover la regla.

La función de partición cuenta las particiones de un número entero no negativo . Por ejemplo, porque el número entero tiene las cinco particiones , , , y . Los valores de esta función para son: ${\displaystyle p(n)}$ ${\displaystyle n}$ ${\displaystyle p(4)=5}$ ${\displaystyle 4}$ ${\displaystyle 1+1+1+1}$ ${\displaystyle 1+1+2}$ ${\displaystyle 1+3}$ ${\displaystyle 2+2}$ ${\displaystyle 4}$ ${\displaystyle n=0,1,2,\dots }$

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604,... (secuencia A000041 en la OEIS ).

La función generadora de es ${\displaystyle p}$

${\displaystyle \sum _{n=0}^{\infty }p(n)q^{n}=\prod _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.}$

No se conoce ninguna expresión de forma cerrada para la función de partición, pero tiene expansiones asintóticas que la aproximan con precisión y relaciones de recurrencia mediante las cuales se puede calcular exactamente. Crece como función exponencial de la raíz cuadrada de su argumento, ^[3] de la siguiente manera:

${\displaystyle p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)}$como ${\displaystyle n\to \infty }$

En 1937, Hans Rademacher había descubierto una manera de representar la función de partición mediante series convergentes . ${\displaystyle p(n)}$

$${\displaystyle p(n)={\frac {1}{\pi {\sqrt {2}}}}\sum _{k=1}^{\infty }A_{k}(n){\sqrt {k}}\cdot {\frac {d}{dn}}\left({{\frac {1}{\sqrt {n-{\frac {1}{24}}}}}\sinh \left[{{\frac {\pi }{k}}{\sqrt {{\frac {2}{3}}\left(n-{\frac {1}{24}}\right)}}}\,\,\,\right]}\right)}$$

$${\displaystyle A_{k}(n)=\sum _{0\leq m<k,\;(m,k)=1}e^{\pi i\left(s(m,k)-2nm/k\right)}.}$$

suma de Dedekind ${\displaystyle s(m,k)}$

La inversa multiplicativa de su función generadora es la función de Euler ; Según el teorema de los números pentagonales de Euler , esta función es una suma alterna de potencias de números pentagonales de su argumento.

${\displaystyle p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots }$

Srinivasa Ramanujan descubrió que la función de partición tiene patrones no triviales en la aritmética modular , ahora conocidos como congruencias de Ramanujan . Por ejemplo, siempre que la representación decimal de termine en el dígito 4 o 9, el número de particiones será divisible por 5. ^[4] ${\displaystyle n}$ ${\displaystyle n}$

Particiones restringidas

Tanto en combinatoria como en teoría de números, a menudo se estudian familias de particiones sujetas a diversas restricciones. ^[5] Esta sección examina algunas de esas restricciones.

Particiones conjugadas y autoconjugadas

Si volteamos el diagrama de la partición 6 + 4 + 3 + 1 por su diagonal principal, obtenemos otra partición de 14:

Al convertir las filas en columnas, obtenemos la partición 4 + 3 + 3 + 2 + 1 + 1 del número 14. Se dice que tales particiones son conjugadas entre sí. ^[6] En el caso del número 4, las particiones 4 y 1 + 1 + 1 + 1 son pares conjugados, y las particiones 3 + 1 y 2 + 1 + 1 son pares conjugados entre sí. De particular interés son las particiones, como 2 + 2, que se tienen a sí mismas como conjugadas. Se dice que tales particiones son autoconjugadas . ^[7]

Reclamación : El número de particiones autoconjugadas es el mismo que el número de particiones con partes impares distintas.

Prueba (esquema) : La observación crucial es que cada parte impar se puede " doblar " por la mitad para formar un diagrama autoconjugado:

Entonces se puede obtener una biyección entre el conjunto de particiones con partes impares distintas y el conjunto de particiones autoconjugadas, como se ilustra en el siguiente ejemplo:

Partes impares y partes distintas

Entre las 22 particiones del número 8, hay 6 que contienen sólo partes impares :

• 7 + 1
• 5 + 3
• 5+1+1+1
• 3+3+1+1
• 3+1+1+1+1+1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Alternativamente, podríamos contar particiones en las que ningún número aparece más de una vez. Tal partición se llama partición con partes distintas . Si contamos las particiones de 8 con partes distintas, obtenemos también 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4+3+1

Ésta es una propiedad general. Para cada número positivo, el número de particiones con partes impares es igual al número de particiones con partes distintas, denotado por q ( n ). ^{[8] [9]} Este resultado fue demostrado por Leonhard Euler en 1748 ^[10] y posteriormente se generalizó como el teorema de Glaisher .

Para cada tipo de partición restringida existe una función correspondiente para el número de particiones que satisfacen la restricción dada. Un ejemplo importante es q ( n ) (particiones en partes distintas). Los primeros valores de q ( n ) son (comenzando con q (0) = 1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (secuencia A000009 en el OEIS ).

La función generadora de q ( n ) viene dada por ^[11]

${\displaystyle \sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.}$

El teorema del número pentagonal da una recurrencia para q : ^[12]

q ( ​​k ) = a _k + q ( k − 1) + q ( k − 2) − q ( k − 5) − q ( k − 7) + q ( k − 12) + q ( k − 15) − q ( k − 22) − ...

donde a _k es (−1) ^m si k = 3 m ² − m para algún número entero my es 0 en caso contrario.

Tamaño de pieza restringido o número de piezas

Al tomar conjugados, el número p _k ( n ) de particiones de n en exactamente k partes es igual al número de particiones de n en las que la parte más grande tiene tamaño k . La función p _k ( n ) satisface la recurrencia

p _k ( norte ) = p _k ( norte − k ) + p _{k −1} ( norte − 1 )

con valores iniciales p ₀ (0) = 1 y p _k ( n ) = 0 si n ≤ 0 o k ≤ 0 y n y k no son ambos cero. ^[13]

Se recupera la función p ( n ) por

${\displaystyle p(n)=\sum _{k=0}^{n}p_{k}(n).}$

Una posible función generadora para tales particiones, tomando k fijo y n variable, es

${\displaystyle \sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.}$

De manera más general, si T es un conjunto de números enteros positivos, entonces el número de particiones de n , todas cuyas partes pertenecen a T , tiene función generadora.

${\displaystyle \prod _{t\in T}(1-x^{t})^{-1}.}$

Esto se puede utilizar para resolver problemas de realización de cambios (donde el conjunto T especifica las monedas disponibles). Como dos casos particulares, uno tiene que el número de particiones de n en las que todas las partes son 1 o 2 (o, de manera equivalente, el número de particiones de n en 1 o 2 partes) es

${\displaystyle \left\lfloor {\frac {n}{2}}+1\right\rfloor ,}$

y el número de particiones de n en las que todas las partes son 1, 2 o 3 (o, de manera equivalente, el número de particiones de n en como máximo tres partes) es el entero más cercano a ( n + 3) ^2/12 . ^{[14 ]}

Particiones en un rectángulo y coeficientes binomiales gaussianos.

También se puede limitar simultáneamente el número y el tamaño de las piezas. Sea p ( N , M ; n ) el número de particiones de n con como máximo M partes, cada una de tamaño como máximo N. De manera equivalente, estas son las particiones cuyo diagrama de Young cabe dentro de un rectángulo M × N. Hay una relación de recurrencia.

$${\displaystyle p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)}$$

nMNn − MM^[15] ${\displaystyle p(N,M;n)-p(N,M-1;n)}$

El coeficiente binomial gaussiano se define como:

$${\displaystyle {k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.}$$

función generadorap ( N , M ; n )

$${\displaystyle \sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.}$$

Plaza Rank y Durfee

El rango de una partición es el número más grande k tal que la partición contenga al menos k partes de tamaño al menos k . Por ejemplo, la partición 4 + 3 + 3 + 2 + 1 + 1 tiene rango 3 porque contiene 3 partes que son ≥ 3, pero no contiene 4 partes que son ≥ 4. En el diagrama de Ferrers o diagrama de Young de una partición de rango r , el cuadrado r × r de entradas en la parte superior izquierda se conoce como cuadrado de Durfee :

El cuadrado de Durfee tiene aplicaciones dentro de la combinatoria en las pruebas de varias identidades de partición. ^[16] También tiene algún significado práctico en la forma del índice h .

A veces, una estadística diferente también se denomina rango de una partición (o rango de Dyson), es decir, la diferencia para una partición de k partes con la parte más grande . Esta estadística (que no tiene relación con la descrita anteriormente) aparece en el estudio de las congruencias de Ramanujan . ${\displaystyle \lambda _{k}-k}$ ${\displaystyle \lambda _{k}}$

celosía de joven

Existe un orden parcial natural en las particiones dado por la inclusión de diagramas de Young. Este conjunto parcialmente ordenado se conoce como red de Young . La red se definió originalmente en el contexto de la teoría de la representación , donde se utiliza para describir las representaciones irreducibles de grupos simétricos S _n para todo n , junto con sus propiedades de ramificación, en característica cero. También ha recibido importantes estudios por sus propiedades puramente combinatorias; notablemente, es el ejemplo motivador de un poset diferencial .

particiones aleatorias

Existe una teoría profunda de particiones aleatorias elegidas de acuerdo con la distribución de probabilidad uniforme en el grupo simétrico a través de la correspondencia Robinson-Schensted . En 1977, Logan y Shepp, así como Vershik y Kerov, demostraron que el diagrama de Young de una partición grande típica se acerca asintóticamente a la gráfica de una determinada función analítica que minimiza un determinado funcional. En 1988, Baik, Deift y Johansson ampliaron estos resultados para determinar la distribución de la subsecuencia creciente más larga de una permutación aleatoria en términos de la distribución de Tracy-Widom . ^[17] Okounkov relacionó estos resultados con la combinatoria de las superficies de Riemann y la teoría de la representación. ^{[18] [19]}

Ver también

• Rango de una partición , una noción diferente de rango
• Manivela de una partición
• orden de dominancia
• Factorización
• factorización de enteros
• Partición de un conjunto
• Estrellas y barras (combinatoria)
• Partición plana
• Número cortés , definido por particiones en números enteros consecutivos
• partición multiplicativa
• Doce caminos
• Fórmula de muestreo de Ewens
• La fórmula de Faà di Bruno
• Multipartición
• Las identidades de Newton
• Función de piezas más pequeñas
• Una partición de Goldbach es la partición de un número par en números primos (ver la conjetura de Goldbach )
• Función de partición de Kostant

Notas

1. Andrews 1976, pág. 199.
2. Josuat-Vergès, Matthieu (2010), "Biyecciones entre rellenos de diagramas de Young que evitan patrones", Journal of Combinatorial Theory , Serie A, 117 (8): 1218–1230, arXiv : 0801.4928 , doi :10.1016/j.jcta .2010.03.006, SEÑOR  2677686, S2CID  15392503.
3. Andrews 1976, pág. 69.
4. Hardy y Wright 2008, pág. 380.
5. Aliso, Henry L. (1969). "Identidades de partición: desde Euler hasta el presente". Mensual Matemático Estadounidense . 76 (7): 733–746. doi :10.2307/2317861. JSTOR  2317861.
6. Hardy y Wright 2008, pág. 362.
7. Hardy y Wright 2008, pág. 368.
8. Hardy y Wright 2008, pág. 365.
9. La notación sigue a Abramowitz y Stegun 1964, p. 825
10. Andrews, George E. (1971). Teoría de los números . Filadelfia: WB Saunders Company. págs. 149–50.
11. Abramowitz y Stegun 1964, pág. 825, 24.2.2 eq. Yo(B)
12. Abramowitz y Stegun 1964, pág. 826, 24.2.2 eq. II(A)
13. Richard Stanley, Combinatoria enumerativa , volumen 1, segunda edición. Cambridge University Press, 2012. Capítulo 1, sección 1.7.
14. Resistente, GH (1920). Algunos problemas famosos de la teoría de números. Prensa de Clarendon.
15. Andrews 1976, págs. 33-34.
16. ver, por ejemplo, Stanley 1999, p. 58
17. Romik, Dan (2015). "La sorprendente matemática de las subsecuencias crecientes más largas ". Instituto de Libros de Texto de Estadística Matemática. Nueva York: Cambridge University Press. ISBN 978-1-107-42882-9.
18. Okounkov, Andrei (2000). "Matrices aleatorias y permutaciones aleatorias". Avisos internacionales de investigación en matemáticas . 2000 (20): 1043. doi : 10.1155/S1073792800000532 . S2CID  14308256.
19. Okounkov, A. (1 de abril de 2001). "Cuña infinita y particiones aleatorias". Selecta Matemática . 7 (1): 57–81. arXiv : matemáticas/9907127 . doi :10.1007/PL00001398. ISSN  1420-9020. S2CID  119176413.

Referencias

• Abramowitz, Milton ; Stegun, Irene (1964). Manual de funciones matemáticas con fórmulas, gráficas y tablas matemáticas . Departamento de Comercio de Estados Unidos, Oficina Nacional de Normas. ISBN 0-486-61272-4.
• Andrews, George E. (1976). La teoría de las particiones . Prensa de la Universidad de Cambridge. ISBN 0-521-63766-X.
• Andrews, George E.; Eriksson, Kimmo (2004). Particiones enteras . Prensa de la Universidad de Cambridge. ISBN 0-521-60090-1.
• Apóstol, Tom M. (1990) [1976]. Funciones modulares y series de Dirichlet en teoría de números . Textos de Posgrado en Matemáticas . vol. 41 (2ª ed.). Nueva York, etc.: Springer-Verlag . ISBN 0-387-97127-0. Zbl  0697.10023. (Ver el capítulo 5 para una introducción pedagógica moderna a la fórmula de Rademacher) .
• Bóna, Miklós (2002). Un recorrido por la combinatoria: una introducción a la enumeración y la teoría de grafos . Publicaciones científicas mundiales. ISBN 981-02-4900-4.(una introducción elemental al tema de las particiones enteras, incluida una discusión sobre los gráficos de Ferrers)
• Hardy, GH ; Wright, EM (2008) [1938]. Introducción a la teoría de los números . Revisado por DR Heath-Brown y JH Silverman . Prólogo de Andrew Wiles . (6ª ed.). Oxford: Prensa de la Universidad de Oxford . ISBN 978-0-19-921986-5. SEÑOR  2445243. Zbl  1159.11001.
• Lehmer, DH (1939). "Sobre el resto y convergencia de la serie para la función de partición". Trans. América. Matemáticas. Soc . 46 : 362–373. doi : 10.1090/S0002-9947-1939-0000410-9 . Señor  0000410. Zbl  0022.20401.Proporciona la fórmula principal (sin derivados), el resto y la forma anterior de A _k ( n ).)
• Gupta, Hansraj; Gwyther, CE; Miller, JCP (1962). Real Sociedad de Matemáticas. Mesas . vol. 4, Tablas de particiones. (Tiene texto y bibliografía casi completa, pero ellos (y Abramowitz) omitieron la fórmula de Selberg para A _k ( n ), que está en Whiteman).
• Macdonald, Ian G. (1979). Funciones simétricas y polinomios de Hall . Monografías de matemáticas de Oxford. Prensa de la Universidad de Oxford . ISBN 0-19-853530-9. Zbl  0487.20007.(Ver apartado I.1)
• Nathanson, MB (2000). Métodos elementales en teoría de números . Textos de Posgrado en Matemáticas. vol. 195. Springer-Verlag . ISBN 0-387-98912-9. Zbl  0953.11002.
• Rademacher, Hans (1974). Documentos recopilados de Hans Rademacher . vol. vII. Prensa del MIT. págs. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). La Música de los Primos . Nueva York: Perennial-HarperCollins. ISBN 9780066210704.
• Stanley, Richard P. (1999). Combinatoria enumerativa. vol. 1 y 2. Prensa de la Universidad de Cambridge. ISBN 0-521-56069-1.
• Whiteman, AL (1956). "Una suma relacionada con la serie para la función de partición". Revista Pacífico de Matemáticas . 6 (1): 159–176. doi : 10.2140/pjm.1956.6.159 . Zbl  0071.04004. (Proporciona la fórmula de Selberg. La forma más antigua es la expansión finita de Fourier de Selberg).

enlaces externos

• "Partición", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Calculadora de particiones y composiciones.
• Weisstein, Eric W. "Partición". MundoMatemático .
• Wilf, Herbert S. Conferencias sobre particiones enteras (PDF) , archivadas (PDF) desde el original el 24 de febrero de 2021 , consultado el 28 de febrero de 2021
• Contar con particiones con tablas de referencia a la Enciclopedia On-Line de Secuencias Enteras
• Entrada de particiones enteras en la base de datos FindStat
• Integer::Módulo Partition Perl de CPAN
• Algoritmos rápidos para generar particiones enteras
• Generando todas las particiones: una comparación de dos codificaciones
• Grime, James (28 de abril de 2016). «Particiones - Numéfilo» (vídeo) . Brady Harán . Archivado desde el original el 11 de diciembre de 2021 . Consultado el 5 de mayo de 2016 .