El juego de la gallina , también conocido como juego del halcón-paloma o juego del ventisquero , [1] es un modelo de conflicto para dos jugadores en la teoría de juegos . El principio del juego es que, si bien el resultado ideal es que un jugador ceda (para evitar el peor resultado si ninguno cede), los individuos intentan evitarlo por orgullo, no queriendo parecer "pollos". Cada jugador se burla del otro para aumentar el riesgo de vergüenza al ceder. Sin embargo, cuando un jugador cede, el conflicto se evita y el juego esencialmente termina.
El nombre "pollo" tiene su origen en un juego en el que dos conductores conducen uno hacia el otro en rumbo de colisión: uno debe desviarse, o ambos pueden morir en el choque, pero si un conductor se desvía y el otro no, el que desviado será llamado "pollo", es decir, cobarde; esta terminología es más frecuente en ciencias políticas y economía . El nombre "halcón-paloma" se refiere a una situación en la que hay una competencia por un recurso compartido y los concursantes pueden elegir entre la conciliación o el conflicto; esta terminología se usa más comúnmente en biología y teoría de juegos evolutivos . Desde el punto de vista de la teoría de juegos, "pollo" y "halcón-paloma" son idénticos. [1] El juego también se ha utilizado para describir la destrucción mutua asegurada de la guerra nuclear , especialmente el tipo de política arriesgada involucrada en la crisis de los misiles cubanos . [2]
El juego de la gallina modela a dos conductores, ambos se dirigen hacia un puente de un solo carril desde direcciones opuestas. El primero en desviarse le cede el puente al otro. Si ninguno de los jugadores se desvía, el resultado es un costoso punto muerto en medio del puente o una colisión frontal potencialmente fatal. Se presume que lo mejor para cada conductor es mantenerse derecho mientras el otro se desvía (ya que el otro es el "pollo" mientras se evita un choque). Además, se presume que una caída será el peor resultado para ambos jugadores. Esto produce una situación en la que cada jugador, al intentar conseguir el mejor resultado, se arriesga a lo peor.
La frase juego de la gallina también se utiliza como metáfora de una situación en la que dos partes se involucran en un enfrentamiento en el que no tienen nada que ganar y sólo el orgullo les impide dar marcha atrás. Bertrand Russell comparó el juego de la gallina con la política nuclear :
Desde que el estancamiento nuclear se hizo evidente, los gobiernos del Este y del Oeste han adoptado la política que Dulles llama "política arriesgada". Se trata de una política adaptada de un deporte que, según me han dicho, practican algunos jóvenes degenerados. Este deporte se llama '¡Pollo!'. Se juega eligiendo una carretera larga y recta con una línea blanca en el medio y haciendo avanzar dos coches muy rápidos uno hacia el otro desde extremos opuestos. Se espera que cada automóvil mantenga las ruedas a un lado de la línea blanca. A medida que se acercan, la destrucción mutua se vuelve cada vez más inminente. Si uno de ellos se desvía de la línea blanca antes que el otro, el otro, al pasar, grita "¡Pollo!", y el que se ha desviado se convierte en objeto de desprecio. Tal como lo juegan niños irresponsables, este juego se considera decadente e inmoral, aunque solo se arriesgan las vidas de los jugadores. Pero cuando el juego lo juegan eminentes estadistas, que arriesgan no sólo sus propias vidas sino las de muchos cientos de millones de seres humanos, se piensa en ambos lados que los estadistas de un lado están haciendo gala de un alto grado de sabiduría y coraje, y sólo los estadistas del otro lado son reprensibles. Esto, por supuesto, es absurdo. Ambos tienen la culpa de jugar un juego tan increíblemente peligroso. Puede que el juego se juegue sin desgracias unas cuantas veces, pero tarde o temprano se llegará a sentir que la pérdida de prestigio es más terrible que la aniquilación nuclear. Llegará el momento en que ninguno de los bandos podrá afrontar el grito burlón de '¡Pollo!' desde el otro lado. Cuando llegue ese momento, los estadistas de ambos lados hundirán al mundo en la destrucción. [2]
La política arriesgada implica la introducción de un elemento de riesgo incontrolable: incluso si todos los actores actúan racionalmente frente al riesgo, los eventos incontrolables aún pueden desencadenar un resultado catastrófico. [3] En la escena "Chickie Run" de la película Rebelde sin causa , esto sucede cuando Buzz no puede escapar del auto y muere en el accidente. El escenario opuesto ocurre en Footloose , donde Ren McCormack queda atrapado en su tractor y, por lo tanto, gana el juego ya que no pueden jugar al "pollo". Un evento similar ocurre en dos juegos diferentes de la película The Heavenly Kid , cuando primero Bobby y luego Lenny quedan atrapados en sus autos y se caen por un acantilado. La formulación básica de la teoría de juegos de Chicken no tiene ningún elemento de riesgo variable, potencialmente catastrófico, y también es la contracción de una situación dinámica en una interacción de una sola vez.
La versión del juego halcón-paloma imagina a dos jugadores (animales) disputando un recurso indivisible que pueden elegir entre dos estrategias, una más intensificada que la otra. [4] Pueden usar exhibiciones de amenaza (jugar a Paloma) o atacarse físicamente entre sí (jugar a Halcón). Si ambos jugadores eligen la estrategia Hawk, lucharán hasta que uno resulte herido y el otro gane. Si solo un jugador elige a Hawk, entonces este jugador derrota al jugador de Dove. Si ambos jugadores juegan contra la Paloma, hay un empate y cada jugador recibe una recompensa menor que la ganancia de un halcón que derrota a una paloma.
Una versión formal del juego del Pollo ha sido objeto de serias investigaciones en teoría de juegos . [5] Aquí se presentan dos versiones de la matriz de pagos para este juego (Figuras 1 y 2). En la Figura 1, los resultados se representan en palabras, donde cada jugador preferiría ganar antes que empatar, preferiría empatar antes que perder y preferiría perder antes que chocar. La Figura 2 presenta pagos numéricos establecidos arbitrariamente que teóricamente se ajustan a esta situación. Aquí, el beneficio de ganar es 1, el costo de perder es -1 y el costo de estrellarse es -1000.
Tanto Chicken como Hawk-Dove son juegos anti-coordinación , en los que es mutuamente beneficioso para los jugadores jugar diferentes estrategias. De esta manera, se puede pensar como lo opuesto a un juego de coordinación , donde jugando la misma estrategia Pareto domina jugando diferentes estrategias. El concepto subyacente es que los jugadores utilizan un recurso compartido. En los juegos de coordinación, compartir el recurso crea un beneficio para todos: el recurso no es rival y el uso compartido crea externalidades positivas . En los juegos contra la coordinación, el recurso es rival pero no excluyente y compartirlo tiene un costo (o una externalidad negativa).
Debido a que la pérdida de desvío es tan trivial en comparación con el choque que ocurre si nadie se desvía, la estrategia razonable parecería ser desviarse antes de que sea probable que se produzca un choque. Sin embargo, sabiendo esto, si uno cree que su oponente es razonable, bien puede decidir no desviarse en absoluto, creyendo que el oponente será razonable y decidir desviarse, dejando al primer jugador como ganador. Esta situación inestable se puede formalizar diciendo que hay más de un equilibrio de Nash , que es un par de estrategias en las que ningún jugador gana al cambiar su propia estrategia mientras el otro permanece igual. (En este caso, los equilibrios estratégicos puros son las dos situaciones en las que un jugador se desvía mientras el otro no).
En la literatura biológica , este juego se conoce como Halcón-Paloma. La primera presentación de una forma del juego Halcón-Paloma fue la de John Maynard Smith y George Price en su artículo "La lógica del conflicto animal". [6] La matriz de pagos tradicional [4] [7] para el juego Halcón-Paloma se muestra en la Figura 3, donde V es el valor del recurso en disputa y C es el costo de una pelea intensificada. (Casi siempre) se supone que el valor del recurso es menor que el costo de una pelea, es decir, C > V > 0. Si C ≤ V, el juego resultante no es un juego de Pollo sino un Dilema del Prisionero. .
El valor exacto del pago de Dove vs. Dove varía según las formulaciones del modelo. A veces se supone que los jugadores dividen la recompensa en partes iguales (V/2 cada uno), otras veces se supone que la recompensa es cero (ya que esta es la recompensa esperada en un juego de guerra de desgaste , que son los supuestos modelos para una competencia decidida por duración de la visualización).
Si bien el juego Halcón-Paloma normalmente se enseña y analiza con los resultados en términos de V y C, las soluciones son válidas para cualquier matriz con los resultados de la Figura 4, donde W > T > L > X. [7]
Los biólogos han explorado versiones modificadas del clásico juego Halcón-Paloma para investigar una serie de factores biológicamente relevantes. Estos incluyen agregar variación en el potencial de retención de recursos y diferencias en el valor de ganar para los diferentes jugadores, [8] permitir que los jugadores se amenacen entre sí antes de elegir movimientos en el juego, [9] y extender la interacción a dos jugadas del juego. juego. [10]
Una táctica en el juego es que una de las partes indique sus intenciones de manera convincente antes de que comience el juego. Por ejemplo, si una de las partes desactivara ostentosamente su volante justo antes del partido, la otra parte se vería obligada a desviarse. [11] Esto muestra que, en algunas circunstancias, reducir las propias opciones puede ser una buena estrategia. Un ejemplo del mundo real es el de un manifestante que se esposa a un objeto, de modo que no se le pueda hacer ninguna amenaza que le obligue a moverse (ya que no puede moverse). Otro ejemplo, tomado de la ficción, lo encontramos en Dr. Strangelove, de Stanley Kubrick . En esa película, los rusos intentaron disuadir el ataque estadounidense construyendo una "máquina del fin del mundo", un dispositivo que desencadenaría la aniquilación mundial si Rusia fuera alcanzada por armas nucleares o si se intentara desarmarla. Sin embargo, los rusos habían planeado señalar el despliegue de la máquina algunos días después de haberla instalado, lo que, debido al desafortunado curso de los acontecimientos, resultó demasiado tarde.
Los jugadores también pueden hacer amenazas no vinculantes para no desviarse. Esto ha sido modelado explícitamente en el juego Halcón-Paloma. Tales amenazas funcionan, pero deben ser muy costosas si la amenaza es una de dos señales posibles ("No me desviaré" o "Me desviaré"), o no tendrán costo si hay tres o más señales (en cuyo caso la Las señales funcionarán como un juego de " piedra, papel o tijera "). [9]

Todos los juegos anticoordinación tienen tres equilibrios de Nash . Dos de ellos son perfiles de estrategia puramente contingentes, en los que cada jugador juega una de las dos estrategias y el otro jugador elige la estrategia opuesta. El tercero es un equilibrio mixto , en el que cada jugador elige probabilísticamente entre las dos estrategias puras. Los equilibrios de Nash puros o mixtos serán estrategias evolutivamente estables dependiendo de si existen asimetrías no correlacionadas .
El mejor mapeo de respuesta para todos los juegos anticoordinación 2x2 se muestra en la Figura 5. Las variables x e y en la Figura 5 son las probabilidades de jugar la estrategia escalada ("Hawk" o "Don't swerve") para los jugadores X e Y. respectivamente. La línea del gráfico de la izquierda muestra la probabilidad óptima de jugar la estrategia escalada para el jugador Y en función de x . La línea en el segundo gráfico muestra la probabilidad óptima de jugar la estrategia escalada para el jugador X en función de y (los ejes no se han rotado, por lo que la variable dependiente se representa en la abscisa y la variable independiente se representa en la ordenada) . ). Los equilibrios de Nash se dan cuando las correspondencias de los jugadores coinciden, es decir, se cruzan. Estos se muestran con puntos en el gráfico de la derecha. Las mejores asignaciones de respuestas coinciden (es decir, se cruzan) en tres puntos. Los dos primeros equilibrios de Nash están en las esquinas superior izquierda e inferior derecha, donde un jugador elige una estrategia y el otro elige la estrategia opuesta. El tercer equilibrio de Nash es una estrategia mixta que se extiende a lo largo de la diagonal desde la esquina inferior izquierda hasta la superior derecha. Si los jugadores no saben cuál de ellos es cuál, entonces la Nash mixta es una estrategia evolutivamente estable (ESS), ya que el juego se limita a la línea diagonal inferior izquierda a superior derecha. De lo contrario, se dice que existe una asimetría no correlacionada y los equilibrios de Nash de esquina son ESS.
La ESS para el juego Halcón-Paloma es una estrategia mixta. La teoría formal de juegos es indiferente a si esta mezcla se debe a que todos los jugadores de una población eligen aleatoriamente entre las dos estrategias puras (un rango de posibles reacciones instintivas para una sola situación) o si la población es una mezcla polimórfica de jugadores dedicados a elegir una estrategia. estrategia pura particular (una única reacción que difiere de un individuo a otro). Biológicamente, estas dos opciones son ideas sorprendentemente diferentes. El juego Halcón-Paloma se ha utilizado como base para simulaciones evolutivas para explorar cuál de estos dos modos de mezcla debería predominar en la realidad. [12]
Tanto en "Pollo" como en "Hawk-Dove", el único equilibrio de Nash simétrico es el equilibrio de Nash de estrategia mixta , donde ambos individuos eligieron aleatoriamente entre jugar Hawk/Straight o Dove/Swerve. Este equilibrio de estrategias mixtas suele ser subóptimo: ambos jugadores obtendrían mejores resultados si pudieran coordinar sus acciones de alguna manera. Esta observación se ha hecho de forma independiente en dos contextos diferentes, con resultados casi idénticos. [13]
Considere la versión de "Pollo" que se muestra en la Figura 6. Como todas las formas del juego, hay tres equilibrios de Nash . Los dos equilibrios de Nash de estrategia pura son ( D , C ) y ( C , D ). También existe un equilibrio de estrategia mixta en el que cada jugador se atreve con una probabilidad de 1/3. Resulta en pagos esperados de 14/3 = 4,667 para cada jugador.
Ahora considere un tercero (o algún evento natural) que roba una de las tres cartas etiquetadas: ( C , C ), ( D , C ) y ( C , D ). Se supone que este evento de sorteo exógeno es uniformemente aleatorio en los 3 resultados. Después de robar la carta, el tercero informa a los jugadores de la estrategia que se les ha asignado en la carta (pero no de la estrategia asignada a su oponente). Supongamos que a un jugador se le asigna D , no querrá desviarse suponiendo que el otro jugador haya jugado su estrategia asignada, ya que obtendrá 7 (el pago más alto posible). Supongamos que a un jugador se le asigna C. Luego, al otro jugador se le ha asignado C con probabilidad 1/2 y D con probabilidad 1/2 (debido a la naturaleza del sorteo exógeno). La utilidad esperada de Daring es 0(1/2) + 7(1/2) = 3.5 y la utilidad esperada de acobardarse es 2(1/2) + 6(1/2) = 4. Entonces, el jugador Prefiero acobardarme.
Dado que ninguno de los jugadores tiene incentivos para desviarse de las asignaciones sorteadas, esta distribución de probabilidad entre las estrategias se conoce como equilibrio correlacionado del juego. En particular, el pago esperado para este equilibrio es 7(1/3) + 2(1/3) + 6(1/3) = 5, que es mayor que el pago esperado del equilibrio de Nash con estrategias mixtas.
Aunque hay tres equilibrios de Nash en el juego Halcón-Paloma, el que emerge como estrategia evolutivamente estable (EEE) depende de la existencia de cualquier asimetría no correlacionada en el juego (en el sentido de juegos anticoordinación ). Para que los jugadores de fila puedan elegir una estrategia y los de columna otra, los jugadores deben poder distinguir qué rol (jugador de columna o de fila) tienen. Si no existe tal asimetría no correlacionada, entonces ambos jugadores deben elegir la misma estrategia y el ESS será el equilibrio mixto de Nash. Si hay una asimetría no correlacionada, entonces la mezcla de Nash no es una EEE, pero los dos equilibrios de Nash puros y contingentes de roles sí lo son.
La interpretación biológica estándar de esta asimetría no correlacionada es que un jugador es el propietario del territorio, mientras que el otro es un intruso en el territorio. En la mayoría de los casos, el propietario del territorio juega como Halcón mientras que el intruso juega como Paloma. En este sentido, la evolución de las estrategias en Hawk-Dove puede verse como la evolución de una especie de versión prototípica de propiedad. Sin embargo, desde el punto de vista de la teoría de juegos, esta solución no tiene nada de especial. La solución opuesta, donde el dueño hace de paloma y el intruso hace de halcón, es igualmente estable. De hecho, esta solución está presente en determinadas especies de arañas; cuando aparece un invasor, la araña ocupante se va. Para explicar la prevalencia de los derechos de propiedad sobre los "anti-derechos de propiedad" uno debe descubrir una manera de romper esta simetría adicional. [13]

La dinámica del replicador es un modelo simple de cambio de estrategia comúnmente utilizado en la teoría de juegos evolutiva . En este modelo, una estrategia que funciona mejor que el promedio aumenta en frecuencia a expensas de las estrategias que funcionan peor que el promedio. Hay dos versiones de la dinámica del replicador. En una versión, hay una única población que juega contra sí misma. En otro, hay dos modelos poblacionales donde cada población sólo juega contra la otra población (y no contra sí misma).
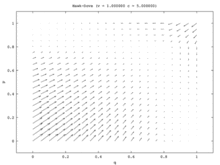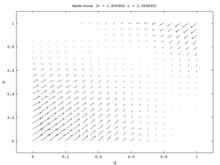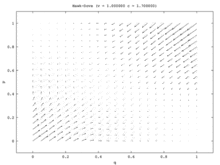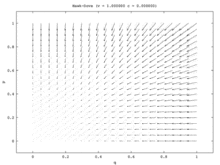
En el modelo de una población, el único estado estable es el equilibrio de Nash de estrategia mixta. Cada proporción de población inicial (excepto toda Hawk y toda Dove ) converge a la estrategia mixta Equilibrio de Nash donde parte de la población juega Hawk y parte de la población juega Dove . (Esto ocurre porque el único ESS es el equilibrio de estrategias mixtas). En el modelo de dos poblaciones, este punto mixto se vuelve inestable. De hecho, los únicos estados estables en el modelo de dos poblaciones corresponden a los equilibrios estratégicos puros, donde una población está compuesta por todos los Hawks y la otra por todos los Dove . En este modelo, una población se convierte en población agresiva mientras que la otra se vuelve pasiva. Este modelo se ilustra mediante el campo vectorial que se muestra en la Figura 7a. El campo vectorial unidimensional del modelo de población única (Figura 7b) corresponde a la diagonal inferior izquierda a superior derecha del modelo de dos poblaciones.

El modelo de población única presenta una situación en la que no existen asimetrías no correlacionadas, por lo que lo mejor que pueden hacer los jugadores es aleatorizar sus estrategias. Los dos modelos de población proporcionan dicha asimetría y los miembros de cada población la utilizarán para correlacionar sus estrategias. En el modelo de dos poblaciones, una población gana a expensas de la otra. Hawk-Dove y Chicken ilustran así un caso interesante en el que los resultados cualitativos de las dos versiones diferentes de la dinámica del replicador difieren enormemente. [14]
"Pollo" y " política arriesgada " se utilizan a menudo como sinónimos en el contexto de un conflicto, pero en el sentido estricto de la teoría de juegos, "política arriesgada" se refiere a un movimiento estratégico diseñado para evitar la posibilidad de que el oponente adopte un comportamiento agresivo. La medida implica una amenaza creíble del riesgo de comportamiento irracional ante la agresión. Si el jugador 1 se mueve unilateralmente a A, un jugador racional 2 no puede tomar represalias ya que (A, C) es preferible a (A, A). Sólo si el jugador 1 tiene motivos para creer que existe un riesgo suficiente de que el jugador 2 responda irracionalmente (normalmente cediendo el control sobre la respuesta, de modo que exista un riesgo suficiente de que el jugador 2 responda con A), el jugador 1 se retractará y aceptará el compromiso. .
Al igual que "Pollo", el juego "Guerra de desgaste" modela la escalada del conflicto, pero difieren en la forma en que el conflicto puede escalar. Chicken modela una situación en la que el resultado catastrófico difiere en especie del resultado agradable, por ejemplo, si el conflicto es sobre vida o muerte. La guerra de desgaste modela una situación en la que los resultados difieren sólo en grados, como un combate de boxeo en el que los contendientes tienen que decidir si el premio final de la victoria vale el costo continuo del deterioro de la salud y la resistencia.
El juego Halcón-Paloma es el modelo teórico de juegos de interacciones agresivas más utilizado en biología. [15] La guerra de desgaste es otro modelo de agresión muy influyente en biología. Los dos modelos investigan cuestiones ligeramente diferentes. El juego Halcón-Paloma es un modelo de escalada y aborda la cuestión de cuándo debe un individuo escalar hacia un combate físico peligrosamente costoso. La guerra de desgaste busca responder a la pregunta de cómo se pueden resolver las contiendas cuando no hay posibilidad de combate físico. La guerra de desgaste es una subasta en la que ambos jugadores pagan la oferta más baja (una subasta de segundo precio en la que todos pagan). Se supone que las ofertas son la duración que el jugador está dispuesto a persistir en realizar una exhibición de amenaza costosa . Ambos jugadores acumulan costos mientras se muestran el uno al otro, el concurso finaliza cuando el individuo que hace la oferta más baja abandona. Entonces ambos jugadores habrán pagado la oferta más baja.
Chicken es un juego simétrico de 2x2 con intereses en conflicto; el resultado preferido es jugar Directo mientras el oponente juega Swerve . De manera similar, el dilema del prisionero es un juego simétrico de 2x2 con intereses en conflicto: el resultado preferido es Desertar mientras el oponente juega Cooperar . PD trata sobre la imposibilidad de la cooperación, mientras que Chicken trata sobre la inevitabilidad del conflicto. El juego iterado puede resolver el PD pero no el Pollo. [dieciséis]
Ambos juegos tienen un resultado cooperativo deseable en el que ambos jugadores eligen la estrategia menos intensificada, Virarse-Vivir en el juego del Pollo y Cooperar-Cooperar en el dilema del prisionero, de modo que los jugadores reciben el pago de Coordinación C (ver tablas a continuación). La tentación de alejarse de este resultado sensato es hacia un movimiento Directo en Pollo y un movimiento Defecto en el dilema del prisionero (generando la recompensa de la tentación , en caso de que el otro jugador use el movimiento menos intensificado). La diferencia esencial entre estos dos juegos es que en el dilema del prisionero, la estrategia Cooperar está dominada, mientras que en Pollo el movimiento equivalente no está dominado ya que los resultados cuando el oponente realiza el movimiento más intensificado ( Directo en lugar de Defecto ) se invierten. .
El término " programar pollo " [17] se utiliza en los círculos de gestión de proyectos y desarrollo de software . La condición ocurre cuando dos o más áreas de un equipo de producto afirman que pueden entregar funciones en una fecha temprana poco realista porque cada una asume que los otros equipos están exagerando las predicciones aún más que ellos. Esta pretensión avanza continuamente de un punto de control del proyecto al siguiente hasta que comienza la integración de funciones o justo antes de que la funcionalidad realmente venza.
La práctica de "programar pollo" [18] a menudo resulta en errores contagiosos en el cronograma debido a las dependencias entre equipos y es difícil de identificar y resolver, ya que lo mejor para cada equipo es no ser el primer portador de malas noticias. . Los impulsores psicológicos que subrayan el comportamiento de "programar la gallina" imitan en muchos sentidos el modelo de conflicto halcón-paloma o ventisquero . [19]
{{cite journal}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link){{cite journal}}: CS1 maint: multiple names: authors list (link){{cite journal}}: CS1 maint: multiple names: authors list (link){{cite journal}}: CS1 maint: multiple names: authors list (link)