En matemáticas y física , vector es un término que se refiere informalmente a algunas cantidades que no pueden expresarse mediante un solo número (un escalar ), o a elementos de algunos espacios vectoriales .
Históricamente, los vectores se introdujeron en geometría y física (normalmente en mecánica ) para cantidades que tienen tanto una magnitud como una dirección, como desplazamientos , fuerzas y velocidad . Dichas cantidades se representan mediante vectores geométricos de la misma manera que las distancias , las masas y el tiempo se representan mediante números reales .
El término vector también se utiliza, en algunos contextos, para las tuplas , que son secuencias finitas (de números u otros objetos) de una longitud fija.
Tanto los vectores geométricos como las tuplas se pueden sumar y escalar, y estas operaciones vectoriales dieron lugar al concepto de espacio vectorial, que es un conjunto dotado de una suma vectorial y una multiplicación escalar que satisfacen algunos axiomas que generalizan las principales propiedades de las operaciones sobre los tipos de vectores anteriores. Un espacio vectorial formado por vectores geométricos se denomina espacio vectorial euclidiano y un espacio vectorial formado por tuplas se denomina espacio vectorial de coordenadas .
En matemáticas se consideran muchos espacios vectoriales, como los cuerpos de extensión , los anillos de polinomios , las álgebras y los espacios funcionales . El término vector no se utiliza generalmente para los elementos de estos espacios vectoriales, y suele reservarse para vectores geométricos, tuplas y elementos de espacios vectoriales no especificados (por ejemplo, cuando se analizan las propiedades generales de los espacios vectoriales).

En matemáticas , física e ingeniería , un vector euclidiano o simplemente un vector (a veces llamado vector geométrico [1] o vector espacial [2] ) es un objeto geométrico que tiene magnitud (o longitud ) y dirección . Los vectores euclidianos se pueden sumar y escalar para formar un espacio vectorial . Una cantidad vectorial es una cantidad física con valores vectoriales , que incluye unidades de medida y posiblemente un soporte , formulada como un segmento de línea dirigido . Un vector se representa con frecuencia gráficamente como una flecha que conecta un punto inicial A con un punto terminal B , [3] y se denota por
Un vector es lo que se necesita para "llevar" el punto A al punto B ; la palabra latina vector significa "portador". [4] Fue utilizada por primera vez por astrónomos del siglo XVIII que investigaban la revolución planetaria alrededor del Sol. [5] La magnitud del vector es la distancia entre los dos puntos, y la dirección se refiere a la dirección del desplazamiento de A a B. Muchas operaciones algebraicas con números reales , como la suma , la resta , la multiplicación y la negación , tienen análogos cercanos para los vectores, [6] operaciones que obedecen a las conocidas leyes algebraicas de conmutatividad , asociatividad y distributividad . Estas operaciones y leyes asociadas califican a los vectores euclidianos como un ejemplo del concepto más generalizado de vectores definidos simplemente como elementos de un espacio vectorial .
Los vectores juegan un papel importante en la física : la velocidad y la aceleración de un objeto en movimiento y las fuerzas que actúan sobre él se pueden describir con vectores. [7] Muchas otras cantidades físicas se pueden considerar útiles como vectores. Aunque la mayoría de ellas no representan distancias (excepto, por ejemplo, la posición o el desplazamiento ), su magnitud y dirección aún se pueden representar mediante la longitud y la dirección de una flecha. La representación matemática de un vector físico depende del sistema de coordenadas utilizado para describirlo. Otros objetos similares a vectores que describen cantidades físicas y se transforman de manera similar bajo cambios del sistema de coordenadas incluyen pseudovectores y tensores . [8]En las ciencias naturales , una cantidad vectorial (también conocida como cantidad física vectorial, vector físico o simplemente vector) es una cantidad física con valor vectorial . [9] [10] Normalmente se formula como el producto de una unidad de medida y un valor numérico vectorial ( sin unidad ), a menudo un vector euclidiano con magnitud y dirección . Por ejemplo, un vector de posición en el espacio físico puede expresarse como tres coordenadas cartesianas con la unidad SI de metros .
En física e ingeniería , particularmente en mecánica , un vector físico puede estar dotado de una estructura adicional en comparación con un vector geométrico. [11] Un vector ligado se define como la combinación de una cantidad vectorial ordinaria y un punto de aplicación o punto de acción . [9] [12] Las cantidades vectoriales ligadas se formulan como un segmento de línea dirigido , con un punto inicial definido además de la magnitud y dirección del vector principal. [9] [11] Por ejemplo, una fuerza en el plano euclidiano tiene dos componentes cartesianos en la unidad SI de newtons y un vector de posición bidimensional acompañante en metros, para un total de cuatro números en el plano (y seis en el espacio). [13] [14] [12] Un ejemplo más simple de un vector ligado es el vector de traslación desde un punto inicial a un punto final; en este caso, el vector ligado es un par ordenado de puntos en el mismo espacio de posición, con todas las coordenadas que tienen la misma dimensión y unidad de cantidad (longitud en metros). [15] [16] Un vector deslizante es la combinación de una cantidad vectorial ordinaria y una línea de aplicación o línea de acción , sobre la cual la cantidad vectorial puede ser trasladada (sin rotaciones). Un vector libre es una cantidad vectorial que tiene un soporte o región de aplicación indefinido ; puede ser trasladada libremente sin consecuencias; un vector de desplazamiento es un ejemplo prototípico de vector libre.
Además de la noción de unidades y soporte, las cantidades vectoriales físicas también pueden diferir de los vectores euclidianos en términos de métrica . Por ejemplo, un evento en el espacio-tiempo puede representarse como un cuatrivector de posición , con una unidad derivada coherente de metros: incluye un vector euclidiano de posición y un componente temporal , t ⋅ c 0 (que involucra la velocidad de la luz ). En ese caso, se adopta la métrica de Minkowski en lugar de la métrica euclidiana .
Las magnitudes vectoriales son una generalización de las magnitudes escalares y pueden generalizarse aún más como magnitudes tensoriales . [16] Los vectores individuales pueden ordenarse en una secuencia a lo largo del tiempo (una serie temporal ), como los vectores de posición que discretizan una trayectoria . Un vector también puede resultar de la evaluación , en un instante particular, de una función continua con valor vectorial (por ejemplo, la ecuación del péndulo ). En las ciencias naturales, el término "magnitud vectorial" también abarca campos vectoriales definidos sobre una región bidimensional o tridimensional del espacio, como la velocidad del viento sobre la superficie de la Tierra.
Los pseudovectores y bivectores también se admiten como magnitudes vectoriales físicas.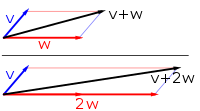
En matemáticas y física , un espacio vectorial (también llamado espacio lineal) es un conjunto cuyos elementos, a menudo llamados vectores , pueden sumarse y multiplicarse ("escalarse") por números llamados escalares . Las operaciones de suma vectorial y multiplicación escalar deben satisfacer ciertos requisitos, llamados axiomas vectoriales . Los espacios vectoriales reales y los espacios vectoriales complejos son tipos de espacios vectoriales basados en diferentes tipos de escalares: números reales y números complejos . Los escalares también pueden ser, de forma más general, elementos de cualquier cuerpo .
Los espacios vectoriales generalizan los vectores euclidianos , que permiten modelar magnitudes físicas , como fuerzas y velocidades , que no solo tienen una magnitud , sino también una dirección . El concepto de espacios vectoriales es fundamental para el álgebra lineal , junto con el concepto de matrices , que permite realizar cálculos en espacios vectoriales. Esto proporciona una forma concisa y sintética de manipular y estudiar sistemas de ecuaciones lineales .
Los espacios vectoriales se caracterizan por su dimensión , que, a grandes rasgos, especifica el número de direcciones independientes en el espacio. Esto significa que, para dos espacios vectoriales sobre un cuerpo dado y con la misma dimensión, las propiedades que dependen solo de la estructura del espacio vectorial son exactamente las mismas (técnicamente, los espacios vectoriales son isomorfos ). Un espacio vectorial es de dimensión finita si su dimensión es un número natural . De lo contrario, es de dimensión infinita , y su dimensión es un cardinal infinito . Los espacios vectoriales de dimensión finita se dan de forma natural en geometría y áreas relacionadas. Los espacios vectoriales de dimensión infinita se dan en muchas áreas de las matemáticas. Por ejemplo, los anillos polinómicos son espacios vectoriales de dimensión infinita numerables , y muchos espacios funcionales tienen la cardinalidad del continuo como dimensión.
Muchos espacios vectoriales que se consideran en matemáticas también están dotados de otras estructuras . Es el caso de las álgebras , que incluyen extensiones de cuerpo , anillos polinómicos, álgebras asociativas y álgebras de Lie . También es el caso de los espacios vectoriales topológicos , que incluyen espacios de funciones, espacios de producto interno , espacios normados , espacios de Hilbert y espacios de Banach .Toda álgebra sobre un cuerpo es un espacio vectorial, pero los elementos de un álgebra no suelen llamarse vectores. Sin embargo, en algunos casos se les denomina vectores , principalmente por razones históricas.
El conjunto de tuplas de n números reales tiene una estructura natural de espacio vectorial definida por la adición de componentes y la multiplicación escalar . Es común llamar a estas tuplas vectores , incluso en contextos donde las operaciones del espacio vectorial no se aplican. De manera más general, cuando algunos datos se pueden representar de manera natural mediante vectores, a menudo se los llama vectores incluso cuando la adición y la multiplicación escalar de vectores no son operaciones válidas sobre estos datos. [ disputado – discutir ] A continuación se presentan algunos ejemplos.
El cálculo sirve como una herramienta matemática fundamental en el ámbito de los vectores, ofreciendo un marco para el análisis y la manipulación de cantidades vectoriales en diversas disciplinas científicas, en particular la física y la ingeniería . Las funciones con valores vectoriales, donde la salida es un vector, se examinan mediante el cálculo para obtener conocimientos esenciales sobre el movimiento dentro del espacio tridimensional. El cálculo vectorial extiende los principios tradicionales del cálculo a los campos vectoriales, introduciendo operaciones como gradiente , divergencia y rizo , que encuentran aplicaciones en contextos de física e ingeniería. Las integrales de línea , cruciales para calcular el trabajo a lo largo de una trayectoria dentro de campos de fuerza, y las integrales de superficie , empleadas para determinar cantidades como el flujo , ilustran la utilidad práctica del cálculo en el análisis vectorial. Las integrales de volumen , esenciales para los cálculos que involucran campos escalares o vectoriales sobre regiones tridimensionales, contribuyen a comprender la distribución de masa , la densidad de carga y las tasas de flujo de fluidos. [ cita requerida ]
Un campo vectorial es una función con valores vectoriales que, generalmente, tiene un dominio de la misma dimensión (como una variedad ) que su codominio,