Felix Christian Klein ( en alemán: [klaɪn] ; 25 de abril de 1849 - 22 de junio de 1925) fue un matemático y educador matemático alemán , conocido por su trabajo en teoría de grupos , análisis complejo , geometría no euclidiana y las asociaciones entre geometría y teoría de grupos . Su programa de Erlangen de 1872 clasificó las geometrías por sus grupos de simetría básicos y fue una síntesis influyente de gran parte de las matemáticas de la época.
Durante su estancia en la Universidad de Göttingen , Klein logró convertirla en un centro de investigación matemática y científica mediante la creación de nuevas cátedras, cátedras e institutos. Sus seminarios abarcaban la mayoría de las áreas de las matemáticas conocidas en aquel momento, así como sus aplicaciones. Klein también dedicó un tiempo considerable a la enseñanza de las matemáticas y promovió la reforma de la enseñanza de las matemáticas en todos los niveles en Alemania y en el extranjero. Se convirtió en el primer presidente de la Comisión Internacional de Enseñanza de las Matemáticas en 1908, en el Cuarto Congreso Internacional de Matemáticos celebrado en Roma.

Felix Klein nació el 25 de abril de 1849 en Düsseldorf , de padres prusianos . Su padre, Caspar Klein (1809-1889), era secretario de un funcionario del gobierno prusiano destinado en la provincia del Rin . Su madre era Sophie Elise Klein (1819-1890, de soltera Kayser ). Asistió al Gymnasium de Düsseldorf, luego estudió matemáticas y física en la Universidad de Bonn , entre 1865 y 1866, con la intención de convertirse en físico. En ese momento, Julius Plücker tenía la cátedra de matemáticas y física experimental de Bonn, pero cuando Klein se convirtió en su asistente, en 1866, el interés de Plücker era principalmente la geometría. Klein recibió su doctorado, supervisado por Plücker, de la Universidad de Bonn en 1868.
Plücker murió en 1868, dejando incompleto su libro sobre las bases de la geometría lineal . Klein era la persona indicada para completar la segunda parte de la Neue Geometrie des Raumes de Plücker , y así conoció a Alfred Clebsch , quien se había mudado a Gotinga en 1868. Klein visitó a Clebsch al año siguiente, junto con visitas a Berlín y París. En julio de 1870, al comienzo de la guerra franco-prusiana , estaba en París y tuvo que abandonar el país. Durante un breve tiempo sirvió como asistente médico en el ejército prusiano antes de ser nombrado Privatdozent (profesor) en Gotinga a principios de 1871.
La Universidad de Erlangen nombró a Klein profesor en 1872, cuando tenía tan solo 23 años. [4] Para ello, recibió el apoyo de Clebsch, que lo consideraba con posibilidades de convertirse en el mejor matemático de su tiempo. Klein no quería permanecer en Erlangen, donde había muy pocos estudiantes, y se alegró de que le ofrecieran una cátedra en la Technische Hochschule München en 1875. Allí, él y Alexander von Brill impartieron cursos avanzados a muchos estudiantes excelentes, entre ellos Adolf Hurwitz , Walther von Dyck , Karl Rohn , Carl Runge , Max Planck , Luigi Bianchi y Gregorio Ricci-Curbastro .
En 1875, Klein se casó con Anne Hegel, nieta del filósofo Georg Wilhelm Friedrich Hegel . [5]
Tras pasar cinco años en la Technische Hochschule, Klein fue nombrado catedrático de geometría en la Universidad de Leipzig . Entre sus colegas se encontraban Walther von Dyck , Rohn, Eduard Study y Friedrich Engel . Los años que Klein pasó en Leipzig, de 1880 a 1886, cambiaron fundamentalmente su vida. En 1882, su salud se deterioró y luchó contra la depresión durante los dos años siguientes. [6] Sin embargo, su investigación continuó; su obra seminal sobre las funciones sigma hiperelípticas, publicada entre 1886 y 1888, data de este período.

Klein aceptó una cátedra en la Universidad de Göttingen en 1886. Desde entonces, hasta su jubilación en 1913, trató de restablecer Göttingen como el principal centro mundial de investigación matemática. Sin embargo, nunca logró transferir de Leipzig a Göttingen su propio papel de líder como desarrollador de la geometría . En Göttingen impartió una variedad de cursos, principalmente sobre la interfaz entre las matemáticas y la física, en particular, mecánica y teoría del potencial .
El centro de investigación que Klein fundó en Gotinga sirvió como modelo para los mejores centros de este tipo en todo el mundo. Introdujo reuniones de debate semanales y creó una sala de lectura matemática y una biblioteca. En 1895, Klein contrató a David Hilbert de la Universidad de Königsberg . Este nombramiento resultó de gran importancia; Hilbert continuó mejorando la primacía de Gotinga en matemáticas hasta su propia jubilación en 1932.
Bajo la dirección editorial de Klein, Mathematische Annalen se convirtió en una de las mejores revistas matemáticas del mundo. Fundada por Clebsch, creció bajo la dirección de Klein hasta rivalizar y, finalmente, superar a Crelle's Journal , con sede en la Universidad de Berlín . Klein estableció un pequeño equipo de editores que se reunían regularmente y tomaban decisiones con un espíritu democrático. La revista se especializó primero en análisis complejo , geometría algebraica y teoría de invariantes . También proporcionó un importante medio para el análisis real y la nueva teoría de grupos .
En 1893, Klein fue un orador importante en el Congreso Internacional de Matemáticas celebrado en Chicago como parte de la Exposición Colombina Mundial . [7] Debido en parte a los esfuerzos de Klein, Gotinga comenzó a admitir mujeres en 1893. Supervisó la primera tesis de doctorado en matemáticas escrita en Gotinga por una mujer, Grace Chisholm Young , una estudiante inglesa de Arthur Cayley , a quien Klein admiraba. En 1897, Klein se convirtió en miembro extranjero de la Real Academia de Artes y Ciencias de los Países Bajos . [8]
Alrededor de 1900, Klein comenzó a interesarse en la enseñanza de las matemáticas en las escuelas. En 1905, fue fundamental en la formulación de un plan que recomendaba que la geometría analítica , los rudimentos del cálculo diferencial e integral y el concepto de función se enseñaran en las escuelas secundarias. [9] [10] Esta recomendación se implementó gradualmente en muchos países de todo el mundo. En 1908, Klein fue elegido presidente de la Comisión Internacional de Instrucción Matemática en el Congreso Internacional de Matemáticos de Roma . [11] Bajo su dirección, la parte alemana de la Comisión publicó muchos volúmenes sobre la enseñanza de las matemáticas en todos los niveles en Alemania.
La Sociedad Matemática de Londres le otorgó a Klein su Medalla De Morgan en 1893. Fue elegido miembro de la Royal Society en 1885 y recibió su Medalla Copley en 1912. Se jubiló al año siguiente debido a problemas de salud, pero continuó enseñando matemáticas en su casa durante varios años más.
Klein fue uno de los noventa y tres firmantes del Manifiesto de los Noventa y Tres , un documento escrito en apoyo de la invasión alemana de Bélgica en las primeras etapas de la Primera Guerra Mundial .
Murió en Gotinga en 1925.
La disertación de Klein, sobre geometría lineal y sus aplicaciones a la mecánica , clasificó los complejos lineales de segundo grado utilizando la teoría de divisores elementales de Weierstrass .
Los primeros descubrimientos matemáticos importantes de Klein se realizaron en 1870. En colaboración con Sophus Lie , descubrió las propiedades fundamentales de las líneas asintóticas en la superficie de Kummer . Más tarde investigaron las curvas W , curvas invariantes bajo un grupo de transformaciones proyectivas . Fue Lie quien introdujo a Klein al concepto de grupo, que tendría un papel importante en su trabajo posterior. Klein también aprendió sobre grupos de Camille Jordan . [12]
Klein ideó la " botella de Klein ", que lleva su nombre, una superficie cerrada de un solo lado que no puede incrustarse en el espacio euclidiano tridimensional , pero puede sumergirse como un cilindro enrollado sobre sí mismo para unirse con su otro extremo desde el "interior". Puede incrustarse en el espacio euclidiano de dimensiones 4 y superiores. El concepto de una botella de Klein fue ideado como una banda de Möbius tridimensional , con un método de construcción que es la unión de los bordes de dos bandas de Möbius . [13]
Durante la década de 1890, Klein comenzó a estudiar física matemática de forma más intensiva, escribiendo sobre el giroscopio con Arnold Sommerfeld . [14] Durante 1894, inició la idea de una enciclopedia de matemáticas que incluyera sus aplicaciones, que se convirtió en la Encyklopädie der mathematischen Wissenschaften . Esta empresa, que perduró hasta 1935, proporcionó una importante referencia estándar de valor perdurable. [15]
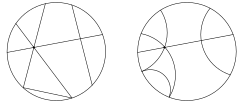
En 1871, mientras estaba en Gotinga, Klein hizo importantes descubrimientos en geometría. Publicó dos artículos Sobre la llamada geometría no euclidiana, en los que demostraba que las geometrías euclidianas y no euclidianas podían considerarse espacios métricos determinados por una métrica de Cayley-Klein . Esta idea tenía como corolario que la geometría no euclidiana era consistente si y solo si la geometría euclidiana lo era, dando el mismo estatus a las geometrías euclidianas y no euclidianas, y poniendo fin a toda controversia sobre la geometría no euclidiana. Arthur Cayley nunca aceptó el argumento de Klein, creyendo que era circular.
La síntesis de la geometría de Klein como el estudio de las propiedades de un espacio que es invariante bajo un grupo dado de transformaciones , conocida como el programa de Erlangen (1872), influyó profundamente en la evolución de las matemáticas. Este programa fue iniciado por la conferencia inaugural de Klein como profesor en Erlangen, aunque no fue el discurso real que pronunció en esa ocasión. El programa proponía un sistema unificado de geometría que se ha convertido en el método moderno aceptado. Klein mostró cómo las propiedades esenciales de una geometría dada podían representarse mediante el grupo de transformaciones que preservan esas propiedades. Por lo tanto, la definición de geometría del programa abarcaba tanto la geometría euclidiana como la no euclidiana.
En la actualidad, la importancia de las contribuciones de Klein a la geometría es evidente. Han pasado a formar parte del pensamiento matemático hasta tal punto que resulta difícil apreciar su novedad cuando se presentan por primera vez y comprender el hecho de que no hayan sido aceptadas inmediatamente por todos sus contemporáneos.
Klein consideró su trabajo sobre análisis complejo como su principal contribución a las matemáticas, específicamente su trabajo sobre:
Klein demostró que el grupo modular mueve la región fundamental del plano complejo de modo que tesela el plano. En 1879, examinó la acción de PSL(2,7) , considerada como una imagen del grupo modular , y obtuvo una representación explícita de una superficie de Riemann ahora denominada cuártica de Klein . Demostró que era una curva compleja en el espacio proyectivo , que su ecuación era x 3 y + y 3 z + z 3 x = 0, y que su grupo de simetrías era PSL(2,7) de orden 168. Su Ueber Riemann's Theorie der algebraischen Funktionen und ihre Integrale (1882) trata el análisis complejo de una manera geométrica, conectando la teoría del potencial y las aplicaciones conformes . Este trabajo se basó en nociones de la dinámica de fluidos .
Klein consideró ecuaciones de grado > 4, y estaba especialmente interesado en utilizar métodos trascendentales para resolver la ecuación general de quinto grado. Basándose en los métodos de Charles Hermite y Leopold Kronecker , produjo resultados similares a los de Brioschi y más tarde resolvió completamente el problema mediante el grupo icosaédrico . Este trabajo le permitió escribir una serie de artículos sobre funciones modulares elípticas .
En su libro de 1884 sobre el icosaedro , Klein estableció una teoría de funciones automorfas , asociando el álgebra y la geometría. Poincaré había publicado un esbozo de su teoría de funciones automorfas en 1881, lo que dio lugar a una rivalidad amistosa entre los dos hombres. Ambos intentaron enunciar y demostrar un gran teorema de uniformización que establecería la nueva teoría de manera más completa. Klein tuvo éxito en la formulación de dicho teorema y en la descripción de una estrategia para demostrarlo. Se le ocurrió su prueba durante un ataque de asma a las 2:30 AM del 23 de marzo de 1882. [16]
Klein resumió su trabajo sobre funciones modulares automórficas y elípticas en un tratado de cuatro volúmenes, escrito con Robert Fricke durante un período de aproximadamente 20 años.