Teorema de pitágoras

Relación entre lados de un triángulo rectángulo

En matemáticas , el teorema de Pitágoras o teorema de Pitágoras es una relación fundamental en la geometría euclidiana entre los tres lados de un triángulo rectángulo . Establece que el área del cuadrado cuyo lado es la hipotenusa (el lado opuesto al ángulo recto ) es igual a la suma de las áreas de los cuadrados de los otros dos lados.

El teorema se puede escribir como una ecuación que relaciona las longitudes de los lados a , b y la hipotenusa c , a veces llamada ecuación pitagórica : ^[1]

${\displaystyle a^{2}+b^{2}=c^{2}.}$

El teorema lleva el nombre del filósofo griego Pitágoras , nacido alrededor del 570 a.C. El teorema ha sido demostrado numerosas veces mediante muchos métodos diferentes, posiblemente el mayor número de cualquier teorema matemático. Las pruebas son diversas, incluidas pruebas geométricas y pruebas algebraicas , y algunas se remontan a miles de años.

Cuando el espacio euclidiano se representa mediante un sistema de coordenadas cartesiano en geometría analítica , la distancia euclidiana satisface la relación pitagórica: la distancia al cuadrado entre dos puntos es igual a la suma de los cuadrados de la diferencia en cada coordenada entre los puntos.

El teorema se puede generalizar de varias maneras: a espacios de dimensiones superiores , a espacios que no son euclidianos , a objetos que no son triángulos rectángulos y a objetos que no son triángulos en absoluto sino sólidos de n dimensiones . El teorema de Pitágoras ha atraído interés fuera de las matemáticas como símbolo de abstrusismo, mística o poder intelectual matemático; Abundan las referencias populares en literatura, obras de teatro, musicales, canciones, estampillas y dibujos animados. ^{[ cita necesaria ]}

Pruebas usando cuadrados construidos.

Prueba de reordenamiento del teorema de Pitágoras.
(El área del espacio en blanco permanece constante durante la reordenación de traslación de los triángulos. En todo momento, el área siempre es c² . Y de la misma manera, en todos los momentos, el área siempre es a²+b² ).

Pruebas de reordenamiento

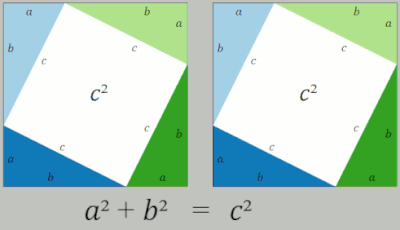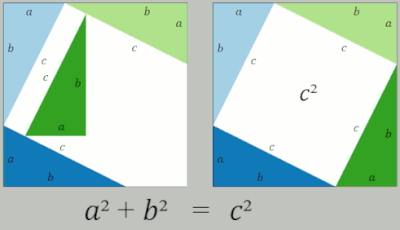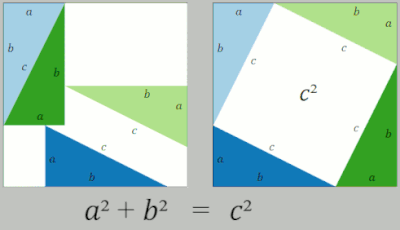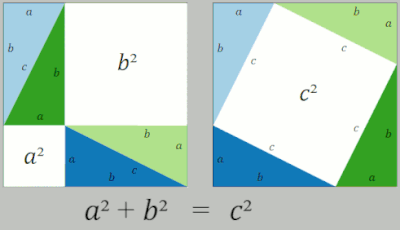
En una prueba de reordenamiento se utilizan dos cuadrados cuyos lados tienen una medida de y que contienen cuatro triángulos rectángulos cuyos lados son a , b y c , siendo la hipotenusa c . En el cuadrado del lado derecho, los triángulos se colocan de manera que las esquinas del cuadrado correspondan a las esquinas del ángulo recto en los triángulos, formando un cuadrado en el centro cuyos lados miden longitud c . Cada cuadrado exterior tiene un área de y representa el área total de los cuatro triángulos. Dentro del cuadrado grande del lado izquierdo, los cuatro triángulos se mueven para formar dos rectángulos similares con lados de longitud a y b . Estos rectángulos en su nueva posición ahora han delineado dos nuevos cuadrados, uno con una longitud de lado a formado en la esquina inferior izquierda y otro cuadrado con una longitud de lado b formado en la esquina superior derecha. En esta nueva posición, este lado izquierdo ahora tiene un cuadrado de área además de . Dado que ambos cuadrados tienen el área de , se deduce que la otra medida del área del cuadrado también es igual a la otra, de modo que = . Eliminando el área de los cuatro triángulos de ambos lados de la ecuación, lo que queda es ^[2] ${\displaystyle a+b}$ ${\displaystyle (a+b)^{2}}$ ${\displaystyle 2ab+c^{2}}$ ${\displaystyle 2ab}$ ${\displaystyle (a+b)^{2}}$ ${\displaystyle 2ab+a^{2}+b^{2}}$ ${\displaystyle (a+b)^{2}}$ ${\displaystyle 2ab+c^{2}}$ ${\displaystyle 2ab+a^{2}+b^{2}}$ ${\displaystyle a^{2}+b^{2}=c^{2}.}$

En otra prueba, los rectángulos en el segundo cuadro también se pueden colocar de modo que ambos tengan una esquina que corresponda a esquinas consecutivas del cuadrado. De esta forma también se forman dos cuadros, esta vez en esquinas consecutivas, con áreas y que darán lugar nuevamente a un segundo cuadrado con el área . ${\displaystyle a^{2}}$ ${\displaystyle b^{2}}$ ${\displaystyle 2ab+a^{2}+b^{2}}$

El matemático inglés Sir Thomas Heath da esta prueba en su comentario a la Proposición I.47 en Los Elementos de Euclides , y menciona las propuestas de los matemáticos alemanes Carl Anton Bretschneider y Hermann Hankel de que Pitágoras pudo haber conocido esta prueba. El propio Heath está a favor de una propuesta diferente para una demostración pitagórica, pero reconoce desde el comienzo de su discusión "que la literatura griega que poseemos perteneciente a los primeros cinco siglos después de Pitágoras no contiene ninguna declaración que especifique este o cualquier otro gran descubrimiento geométrico particular de él. " ^[3] Los estudios recientes han arrojado cada vez más dudas sobre cualquier tipo de papel de Pitágoras como creador de las matemáticas, aunque el debate sobre esto continúa. ^[4]

Pruebas algebraicas

Diagrama de las dos demostraciones algebraicas.

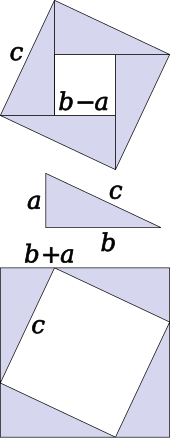
El teorema se puede demostrar algebraicamente usando cuatro copias del mismo triángulo dispuestas simétricamente alrededor de un cuadrado de lado c , como se muestra en la parte inferior del diagrama. ^[5] Esto da como resultado un cuadrado más grande, con lado a + b y área ( a + b ) ² . Los cuatro triángulos y el lado c del cuadrado deben tener la misma área que el cuadrado más grande,

${\displaystyle (b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,}$

donación

${\displaystyle c^{2}=(b+a)^{2}-2ab=b^{2}+2ab+a^{2}-2ab=a^{2}+b^{2}.}$

Una prueba similar utiliza cuatro copias de un triángulo rectángulo con lados a , b y c , dispuestas dentro de un cuadrado con lado c como en la mitad superior del diagrama. ^[6] Los triángulos son semejantes con área , mientras que el cuadrado pequeño tiene lado b − a y área ( b − a ) ² . Por lo tanto, el área del cuadrado grande es ${\displaystyle {\tfrac {1}{2}}ab}$

${\displaystyle (b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=b^{2}-2ab+a^{2}+2ab=a^{2}+b^{2}.}$

Pero este es un cuadrado con lado c y área c ² , entonces

${\displaystyle c^{2}=a^{2}+b^{2}.}$

Otras pruebas del teorema

Este teorema puede tener más pruebas conocidas que cualquier otro (la ley de reciprocidad cuadrática es otro candidato para esa distinción); el libro La proposición pitagórica contiene 370 pruebas. ^[7]

Prueba usando triángulos semejantes

Prueba usando triángulos semejantes

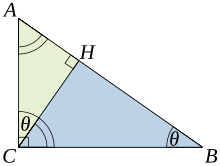
Esta prueba se basa en la proporcionalidad de los lados de tres triángulos semejantes , es decir, en el hecho de que la proporción de dos lados correspondientes cualesquiera de triángulos semejantes es la misma independientemente del tamaño de los triángulos.

Sea ABC un triángulo rectángulo, con el ángulo recto ubicado en C , como se muestra en la figura. Dibuje la altitud desde el punto C y llame a H su intersección con el lado AB . El punto H divide la longitud de la hipotenusa c en las partes d y e . El nuevo triángulo, ACH, es similar al triángulo ABC , porque ambos tienen un ángulo recto (por definición de altitud) y comparten el ángulo en A , lo que significa que el tercer ángulo también será el mismo en ambos triángulos. marcado como θ en la figura. Por un razonamiento similar, el triángulo CBH también es similar a ABC . La prueba de semejanza de los triángulos requiere del postulado del triángulo : La suma de los ángulos de un triángulo es dos ángulos rectos, y equivale al postulado de las paralelas . La similitud de los triángulos conduce a la igualdad de las proporciones de los lados correspondientes:

${\displaystyle {\frac {BC}{AB}}={\frac {BH}{BC}}{\text{ and }}{\frac {AC}{AB}}={\frac {AH}{AC}}.}$

El primer resultado iguala los cosenos de los ángulos θ , mientras que el segundo resultado iguala sus senos .

Estas razones se pueden escribir como

${\displaystyle BC^{2}=AB\times BH{\text{ and }}AC^{2}=AB\times AH.}$

La suma de estas dos igualdades da como resultado

${\displaystyle BC^{2}+AC^{2}=AB\times BH+AB\times AH=AB(AH+BH)=AB^{2},}$

que, después de la simplificación, demuestra el teorema de Pitágoras:

${\displaystyle BC^{2}+AC^{2}=AB^{2}.}$

El papel de esta prueba en la historia es objeto de mucha especulación. La pregunta subyacente es por qué Euclides no utilizó esta prueba, sino que inventó otra. Una conjetura es que la demostración mediante triángulos semejantes involucraba una teoría de proporciones, un tema que no se discutió hasta más adelante en los Elementos , y que la teoría de proporciones necesitaba mayor desarrollo en ese momento. ^[8]

La prueba de Einstein por disección sin reordenamiento

Albert Einstein dio una prueba por disección en la que no es necesario mover las piezas. ^[9] En lugar de usar un cuadrado en la hipotenusa y dos cuadrados en los catetos, se puede usar cualquier otra forma que incluya la hipotenusa y dos formas similares que incluyan cada una uno de dos catetos en lugar de la hipotenusa (ver Figuras similares en la hipotenusa). tres lados). En la prueba de Einstein, la figura que incluye la hipotenusa es el propio triángulo rectángulo. La disección consiste en dejar caer una perpendicular desde el vértice del ángulo recto del triángulo hasta la hipotenusa, dividiendo así todo el triángulo en dos partes. Esas dos partes tienen la misma forma que el triángulo rectángulo original, y tienen los catetos del triángulo original como hipotenusas, y la suma de sus áreas es la del triángulo original. Debido a que la razón entre el área de un triángulo rectángulo y el cuadrado de su hipotenusa es la misma para triángulos similares, la relación entre las áreas de los tres triángulos también se cumple para los cuadrados de los lados del triángulo grande.

Prueba trigonométrica utilizando la construcción de Einstein

Un triángulo rectángulo sobre la hipotenusa se divide en dos triángulos rectángulos similares sobre los catetos, según la demostración de Einstein.

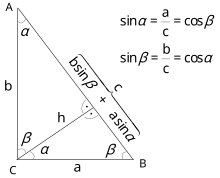
Tanto la prueba que utiliza triángulos semejantes como la prueba de Einstein se basan en construir la altura hasta la hipotenusa del triángulo rectángulo . La misma construcción proporciona una prueba trigonométrica del teorema de Pitágoras utilizando la definición del seno como una razón dentro de un triángulo rectángulo: ${\displaystyle \triangle ABC}$

${\displaystyle \sin \alpha ={\frac {a}{c}},}$

${\displaystyle \sin \beta ={\frac {b}{c}},}$

${\displaystyle c=b\sin \beta +a\sin \alpha ={\frac {b^{2}}{c}}+{\frac {a^{2}}{c}},}$

y por lo tanto

${\displaystyle c^{2}=a^{2}+b^{2}.}$

Esta prueba es esencialmente la misma que la prueba anterior usando triángulos similares, donde algunas razones de longitudes se reemplazan por senos. ^{[ cita necesaria ]}

La prueba de Euclides

Prueba en los elementos de Euclides

En resumen, así es como procede la demostración en los Elementos de Euclides . El cuadrado grande está dividido en un rectángulo izquierdo y derecho. Se construye un triángulo que tiene la mitad del área del rectángulo izquierdo. Luego se construye otro triángulo que tiene la mitad del área del cuadrado en el lado izquierdo. Se muestra que estos dos triángulos son congruentes , lo que demuestra que este cuadrado tiene la misma área que el rectángulo izquierdo. A este argumento le sigue una versión similar para el rectángulo derecho y el cuadrado restante. Juntando los dos rectángulos para reformar el cuadrado sobre la hipotenusa, su área es igual a la suma del área de los otros dos cuadrados. Los detalles siguen.

Sean A , B , C los vértices de un triángulo rectángulo, con un ángulo recto en A . Deja una perpendicular desde A hacia el lado opuesto a la hipotenusa en el cuadrado de la hipotenusa. Esa línea divide el cuadrado de la hipotenusa en dos rectángulos, cada uno de los cuales tiene la misma área que uno de los dos cuadrados de los catetos.

Para la demostración formal, requerimos cuatro lemas elementales :

1. Si dos triángulos tienen dos lados de uno iguales a dos lados del otro, cada uno con cada uno, y los ángulos comprendidos por esos lados son iguales, entonces los triángulos son congruentes ( lado-ángulo-lado ).
2. El área de un triángulo es la mitad del área de cualquier paralelogramo que tenga la misma base y la misma altura.
3. El área de un rectángulo es igual al producto de dos lados adyacentes.
4. El área de un cuadrado es igual al producto de dos de sus lados (se deriva de 3).

A continuación, cada cuadrado superior se relaciona con un triángulo congruente con otro triángulo relacionado a su vez con uno de los dos rectángulos que componen el cuadrado inferior. ^[10]

Ilustración que incluye las nuevas líneas.

Mostrando los dos triángulos congruentes de la mitad del área del rectángulo BDLK y del cuadrado BAGF

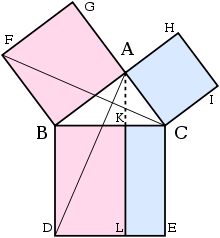
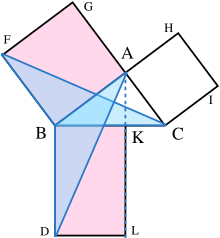
La prueba es como sigue:

1. Sea ACB un triángulo rectángulo con ángulo recto CAB.
2. En cada uno de los lados BC, AB y CA se dibujan cuadrados, CBDE, BAGF y ACIH, en ese orden. La construcción de cuadrados requiere los teoremas inmediatamente anteriores de Euclides y depende del postulado de las paralelas. ^[11]
3. Desde A, traza una línea paralela a BD y CE. Intersectará perpendicularmente a BC y DE en K y L, respectivamente.
4. Une CF y AD, para formar los triángulos BCF y BDA.
5. Los ángulos CAB y BAG son ambos ángulos rectos; por lo tanto C, A y G son colineales .
6. Los ángulos CBD y FBA son ambos ángulos rectos; por lo tanto el ángulo ABD es igual al ángulo FBC, ya que ambos son la suma de un ángulo recto y el ángulo ABC.
7. Como AB es igual a FB, BD es igual a BC y el ángulo ABD es igual al ángulo FBC, el triángulo ABD debe ser congruente con el triángulo FBC.
8. Como AKL es una línea recta paralela a BD, entonces el rectángulo BDLK tiene el doble de área que el triángulo ABD porque comparten la base BD y tienen la misma altura BK, es decir, una línea normal a su base común, que conecta las líneas paralelas BD y ALABAMA. (lema 2)
9. Dado que C es colineal con A y G, y esta línea es paralela a FB, entonces el cuadrado BAGF debe tener el doble de área que el triángulo FBC.
10. Por lo tanto, el rectángulo BDLK debe tener la misma área que el cuadrado BAGF = AB ² .
11. Aplicando los pasos 3 a 10 al otro lado de la figura, se puede demostrar de manera similar que el rectángulo CKLE debe tener la misma área que el cuadrado ACIH = AC ² .
12. Sumando estos dos resultados, AB ² + AC ² = BD × BK + KL × KC
13. Dado que BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
14. Por lo tanto, AB ² + AC ² = BC ² , ya que CBDE es un cuadrado.

Esta prueba, que aparece en los Elementos de Euclides como la de la Proposición 47 del Libro 1, demuestra que el área del cuadrado sobre la hipotenusa es la suma de las áreas de los otros dos cuadrados. ^{[12] [13]} Esto es bastante distinto de la prueba por semejanza de triángulos, que se conjetura que es la prueba que utilizó Pitágoras. ^{[14] [15]}

Pruebas por disección y reordenamiento.

Otro reordenamiento viene dado por la animación del medio. Se forma un cuadrado grande con área c ² , a partir de cuatro triángulos rectángulos idénticos con lados a , b y c , colocados alrededor de un pequeño cuadrado central. Luego se forman dos rectángulos con lados a y b moviendo los triángulos. Combinar el cuadrado más pequeño con estos rectángulos produce dos cuadrados de áreas a ² y b ² , que deben tener la misma área que el cuadrado grande inicial. ^[dieciséis]

La tercera imagen, situada más a la derecha, también da una prueba. Los dos cuadrados superiores están divididos, como se muestra en el sombreado azul y verde, en piezas que, cuando se reorganizan, pueden encajar en el cuadrado inferior de la hipotenusa o, a la inversa, el cuadrado grande se puede dividir, como se muestra, en piezas que llenan los otros dos. . Esta forma de cortar una figura en pedazos y reordenarlos para obtener otra figura se llama disección . Esto muestra que el área del cuadrado grande es igual a la de los dos más pequeños. ^[17]

Prueba mediante cizallamiento con conservación de superficie

Prueba visual del teorema de Pitágoras mediante corte que preserva el área

Como se muestra en la animación adjunta, los mapeos y traslaciones de corte que preservan el área pueden transformar los cuadrados de los lados adyacentes al ángulo recto en el cuadrado de la hipotenusa, cubriéndolo juntos exactamente. ^[18] Cada corte deja la base y la altura sin cambios, por lo que el área tampoco cambia. Las traslaciones también dejan el área sin cambios, ya que no alteran las formas en absoluto. Cada cuadrado se corta primero en un paralelogramo y luego en un rectángulo que se puede trasladar a una sección del cuadrado en la hipotenusa.

Otras pruebas algebraicas

Una prueba relacionada fue publicada por el futuro presidente de los Estados Unidos, James A. Garfield (entonces representante de los Estados Unidos ) (ver diagrama). ^{[19] [20] [21]} En lugar de un cuadrado, utiliza un trapezoide , que se puede construir a partir del cuadrado de la segunda de las pruebas anteriores dividiendo a lo largo de una diagonal del cuadrado interior, para obtener el trapezoide como se muestra en la diagrama. El área del trapezoide se puede calcular como la mitad del área del cuadrado, es decir

${\displaystyle {\frac {1}{2}}(b+a)^{2}.}$

El cuadrado interior se divide de manera similar por la mitad y solo hay dos triángulos, por lo que la prueba procede como se indicó anteriormente, excepto por un factor de , que se elimina multiplicando por dos para obtener el resultado. ${\displaystyle {\frac {1}{2}}}$

Prueba usando diferenciales

Se puede llegar al teorema de Pitágoras estudiando cómo los cambios en un lado producen un cambio en la hipotenusa y empleando cálculo . ^{[22] [23] [24]}

El triángulo ABC es un triángulo rectángulo, como se muestra en la parte superior del diagrama, siendo BC la hipotenusa. Al mismo tiempo se miden las longitudes de los triángulos como se muestra, con la hipotenusa de longitud y , el lado AC de longitud x y el lado AB de longitud a , como se ve en la parte inferior del diagrama.

Diagrama para prueba diferencial.

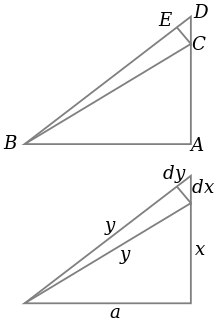
Si x aumenta en una pequeña cantidad dx extendiendo ligeramente el lado AC hacia D , entonces y también aumenta en dy . Estos forman dos lados de un triángulo, CDE , que (con E elegido de modo que CE sea perpendicular a la hipotenusa) es un triángulo rectángulo aproximadamente similar a ABC . Por tanto, las razones de sus lados deben ser iguales, es decir:

${\displaystyle {\frac {dy}{dx}}={\frac {x}{y}}.}$

Esto se puede reescribir como , que es una ecuación diferencial que se puede resolver mediante integración directa: ${\displaystyle y\,dy=x\,dx}$

${\displaystyle \int y\,dy=\int x\,dx\,,}$

donación

${\displaystyle y^{2}=x^{2}+C.}$

La constante se puede deducir de x = 0, y = a para dar la ecuación

${\displaystyle y^{2}=x^{2}+a^{2}.}$

Esta es más una prueba intuitiva que formal: puede hacerse más rigurosa si se utilizan límites adecuados en lugar de dx y dy .

Conversar

Lo inverso del teorema también es cierto: ^[25]

Dado un triángulo con lados de longitud a , b y c , si a ² + b ² = c ² , entonces el ángulo entre los lados a y b es un ángulo recto .

Para tres números reales positivos cualesquiera a , b y c tales que a ² + b ² = c ² , existe un triángulo con lados a , b y c como consecuencia del inverso de la desigualdad del triángulo .

Este inverso aparece en los Elementos de Euclides (Libro I, Proposición 48): "Si en un triángulo el cuadrado de uno de los lados es igual a la suma de los cuadrados de los dos lados restantes del triángulo, entonces el ángulo contenido por los dos lados restantes del triángulo es correcto." ^[26]

Se puede demostrar usando la ley de los cosenos o de la siguiente manera:

Sea ABC un triángulo con lados de longitudes a , b y c , con a ² + b ² = c ² . Construye un segundo triángulo cuyos lados de longitud a y b contengan un ángulo recto. Por el teorema de Pitágoras, se deduce que la hipotenusa de este triángulo tiene longitud c = √ a ² + b ² , la misma que la hipotenusa del primer triángulo. Dado que los lados de ambos triángulos tienen la misma longitud a , b y c , los triángulos son congruentes y deben tener los mismos ángulos. Por lo tanto, el ángulo entre los lados de longitudes a y b en el triángulo original es un ángulo recto.

La demostración anterior de lo contrario hace uso del propio teorema de Pitágoras. Lo contrario también se puede demostrar sin asumir el teorema de Pitágoras. ^{[27] [28]}

Un corolario del inverso del teorema de Pitágoras es un medio sencillo para determinar si un triángulo es rectángulo, obtuso o agudo, de la siguiente manera. Sea c el elegido como el más largo de los tres lados y a + b > c (de lo contrario no hay triángulo según la desigualdad del triángulo ). Se aplican las siguientes declaraciones: ^[29]

• Si a ² + b ² = c ² , entonces el triángulo es rectángulo .
• Si a ² + b ² > c ² , entonces el triángulo es agudo .
• Si a ² + b ² < c ² , entonces el triángulo es obtuso .

Edsger W. Dijkstra ha formulado esta proposición sobre los triángulos agudos, rectángulos y obtusos en este idioma:

sgn( α + β − γ ) = sgn( a ² + segundo ² − c ² ),

donde α es el ángulo opuesto al lado a , β es el ángulo opuesto al lado b , γ es el ángulo opuesto al lado c y sgn es la función de signo . ^[30]

Consecuencias y usos del teorema

Triples pitagóricos

Una terna pitagórica tiene tres números enteros positivos a , b y c , tales que a ² + b ² = c ² . En otras palabras, una terna pitagórica representa las longitudes de los lados de un triángulo rectángulo donde los tres lados tienen longitudes enteras. ^[1] Este triple se escribe comúnmente ( a , b , c ). Algunos ejemplos bien conocidos son (3, 4, 5) y (5, 12, 13).

Una terna pitagórica primitiva es aquella en la que a, byc son coprimos ( el máximo común divisor de a , byc es 1 ) .

La siguiente es una lista de ternas pitagóricas primitivas con valores inferiores a 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Teorema de Pitágoras inverso

Dado un triángulo rectángulo con lados y altura (una recta que parte del ángulo recto y es perpendicular a la hipotenusa ). El teorema de Pitágoras tiene, ${\displaystyle a,b,c}$ ${\displaystyle d}$ ${\displaystyle c}$

${\displaystyle a^{2}+b^{2}=c^{2}}$

mientras que el teorema de Pitágoras inverso relaciona los dos catetos con la altitud , ^[31] ${\displaystyle a,b}$ ${\displaystyle d}$

${\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{d^{2}}}}$

La ecuación se puede transformar a,

${\displaystyle {\frac {1}{(xz)^{2}}}+{\frac {1}{(yz)^{2}}}={\frac {1}{(xy)^{2}}}}$

donde para cualquier real distinto de cero . Si van a ser números enteros , la solución más pequeña es entonces ${\displaystyle x^{2}+y^{2}=z^{2}}$ ${\displaystyle x,y,z}$ ${\displaystyle a,b,d}$ ${\displaystyle a>b>d}$

${\displaystyle {\frac {1}{20^{2}}}+{\frac {1}{15^{2}}}={\frac {1}{12^{2}}}}$

utilizando la terna pitagórica más pequeña . El teorema de Pitágoras recíproco es un caso especial de la ecuación óptica. ${\displaystyle 3,4,5}$

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{r}}}$

donde los denominadores son cuadrados y también para un triángulo heptagonal cuyos lados son números cuadrados. ${\displaystyle p,q,r}$

Longitudes inconmensurables

La espiral de Teodoro : una construcción para segmentos de recta con longitudes cuyas proporciones son la raíz cuadrada de un entero positivo

Una de las consecuencias del teorema de Pitágoras es que los segmentos de recta cuyas longitudes son inconmensurables (por lo que cuya razón no es un número racional ) se pueden construir usando una regla y un compás . El teorema de Pitágoras permite la construcción de longitudes inconmensurables porque la hipotenusa de un triángulo está relacionada con los lados mediante la operación de raíz cuadrada .

La figura de la derecha muestra cómo construir segmentos de línea cuyas longitudes están en la proporción de la raíz cuadrada de cualquier número entero positivo. ^[32] Cada triángulo tiene un lado (etiquetado "1") que es la unidad elegida para medir. En cada triángulo rectángulo, el teorema de Pitágoras establece la longitud de la hipotenusa en términos de esta unidad. Si una hipotenusa está relacionada con la unidad por la raíz cuadrada de un número entero positivo que no es un cuadrado perfecto, es una realización de una longitud inconmensurable con la unidad, como por ejemplo √ 2 , √ 3 , √ 5  . Para obtener más detalles, consulte Irracional cuadrático .

Las longitudes inconmensurables entraban en conflicto con el concepto de la escuela pitagórica de que los números eran únicamente números enteros. La escuela pitagórica trataba las proporciones mediante la comparación de múltiplos enteros de una subunidad común. ^[33] Según una leyenda, Hipaso de Metaponto ( ca. 470 a. C.) se ahogó en el mar por dar a conocer la existencia de lo irracional o inconmensurable. ^[34] Una discusión detallada de las contribuciones de Hippasus se encuentra en Fritz . ^[35]

Números complejos

El valor absoluto de un número complejo z es la distancia r desde z hasta el origen.

Para cualquier número complejo

${\displaystyle z=x+iy,}$

el valor absoluto o módulo está dado por

${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}$

Entonces las tres cantidades, r , x e y están relacionadas por la ecuación pitagórica,

${\displaystyle r^{2}=x^{2}+y^{2}.}$

Tenga en cuenta que r se define como un número positivo o cero, pero xey pueden ser tanto negativos como positivos. Geométricamente r es la distancia de z desde cero o el origen O en el plano complejo .

Esto se puede generalizar para encontrar la distancia entre dos puntos, digamos z ₁ y z ₂ . La distancia requerida está dada por

${\displaystyle |z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}},}$

entonces nuevamente están relacionados por una versión de la ecuación pitagórica,

${\displaystyle |z_{1}-z_{2}|^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}.}$

distancia euclidiana

La fórmula de la distancia en coordenadas cartesianas se deriva del teorema de Pitágoras. ^[36] Si ( x ₁ , y ₁ ) y ( x ₂ , y ₂ ) son puntos en el plano, entonces la distancia entre ellos, también llamada distancia euclidiana , viene dada por

${\displaystyle {\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}$

De manera más general, en el espacio n euclidiano , la distancia euclidiana entre dos puntos, y , se define, por generalización del teorema de Pitágoras, como: ${\displaystyle A\,=\,(a_{1},a_{2},\dots ,a_{n})}$ ${\displaystyle B\,=\,(b_{1},b_{2},\dots ,b_{n})}$

${\displaystyle {\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}}}={\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

Si en lugar de la distancia euclidiana se utiliza el cuadrado de este valor (la distancia euclidiana al cuadrado , o SED), la ecuación resultante evita las raíces cuadradas y es simplemente una suma de las SED de las coordenadas:

${\displaystyle (a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^{2}=\sum _{i=1}^{n}(a_{i}-b_{i})^{2}.}$

La forma al cuadrado es una función suave y convexa de ambos puntos, y se usa ampliamente en teoría de optimización y estadística , formando la base de los mínimos cuadrados .

Distancia euclidiana en otros sistemas de coordenadas

Si no se utilizan coordenadas cartesianas, por ejemplo, si se utilizan coordenadas polares en dos dimensiones o, en términos más generales, si se utilizan coordenadas curvilíneas , las fórmulas que expresan la distancia euclidiana son más complicadas que el teorema de Pitágoras, pero pueden derivarse de él. Un ejemplo típico en el que la distancia en línea recta entre dos puntos se convierte en coordenadas curvilíneas se puede encontrar en las aplicaciones de los polinomios de Legendre en física . Las fórmulas se pueden descubrir utilizando el teorema de Pitágoras con las ecuaciones que relacionan las coordenadas curvilíneas con las coordenadas cartesianas. Por ejemplo, las coordenadas polares ( r , θ ) se pueden introducir como:

${\displaystyle x=r\cos \theta ,\ y=r\sin \theta .}$

Entonces dos puntos con ubicaciones ( r ₁ , θ ₁ ) y ( r ₂ , θ ₂ ) están separados por una distancia s :

${\displaystyle s^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}=(r_{1}\cos \theta _{1}-r_{2}\cos \theta _{2})^{2}+(r_{1}\sin \theta _{1}-r_{2}\sin \theta _{2})^{2}.}$

Realizando los cuadrados y combinando términos, la fórmula pitagórica para distancia en coordenadas cartesianas produce la separación en coordenadas polares como:

${\displaystyle {\begin{aligned}s^{2}&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\left(\cos \theta _{1}\cos \theta _{2}+\sin \theta _{1}\sin \theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left(\theta _{1}-\theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \Delta \theta ,\end{aligned}}}$

usando las fórmulas trigonométricas de producto a suma . Esta fórmula es la ley de los cosenos, a veces llamada teorema de Pitágoras generalizado. ^[37] A partir de este resultado, para el caso en el que los radios de las dos ubicaciones forman ángulos rectos, se recupera el ángulo cerrado Δ θ = π /2, y la forma correspondiente al teorema de Pitágoras: El teorema de Pitágoras, válido para triángulos, por lo tanto, es un caso especial de la ley más general de los cosenos, válida para triángulos arbitrarios. ${\displaystyle s^{2}=r_{1}^{2}+r_{2}^{2}.}$

Identidad trigonométrica pitagórica

Triángulos rectángulos semejantes que muestran seno y coseno del ángulo θ

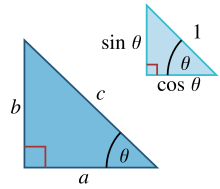
En un triángulo rectángulo con lados a , b e hipotenusa c , la trigonometría determina el seno y el coseno del ángulo θ entre el lado a y la hipotenusa como:

${\displaystyle \sin \theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.}$

De ahí se sigue:

${\displaystyle {\cos }^{2}\theta +{\sin }^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}=1,}$

donde el último paso aplica el teorema de Pitágoras. Esta relación entre seno y coseno a veces se denomina identidad trigonométrica pitagórica fundamental. ^[38] En triángulos similares, las proporciones de los lados son las mismas independientemente del tamaño de los triángulos y dependen de los ángulos. En consecuencia, en la figura, el triángulo con hipotenusa de tamaño unitario tiene un lado opuesto de tamaño sin  θ y un lado adyacente de tamaño cos  θ en unidades de la hipotenusa.

Relación con el producto cruzado

El área de un paralelogramo como producto vectorial; los vectores a y b identifican un plano y a × b es normal a este plano.

El teorema de Pitágoras relaciona el producto cruz y el producto escalar de manera similar: ^[39]

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}+(\mathbf {a} \cdot \mathbf {b} )^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}.}$

Esto se puede ver en las definiciones de producto cruzado y producto escalar, como

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=ab\mathbf {n} \sin {\theta }\\\mathbf {a} \cdot \mathbf {b} &=ab\cos {\theta },\end{aligned}}}$

con n un vector unitario normal a a y b . La relación se deriva de estas definiciones y de la identidad trigonométrica pitagórica.

Esto también se puede utilizar para definir el producto cruzado. Reordenando la siguiente ecuación se obtiene

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

Esto puede considerarse como una condición del producto cruzado y, por lo tanto, parte de su definición, por ejemplo en siete dimensiones . ^{[40] [41]}

como un axioma

Si se supone que los primeros cuatro axiomas de la geometría euclidiana son verdaderos, entonces el teorema de Pitágoras es equivalente al quinto. Es decir, el quinto postulado de Euclides implica el teorema de Pitágoras y viceversa.

Generalizaciones

Figuras similares en los tres lados.

El teorema de Pitágoras se generaliza más allá de las áreas de los cuadrados en los tres lados a cualquier figura similar . Esto lo sabía Hipócrates de Quíos en el siglo V a.C., ^[42] y fue incluido por Euclides en sus Elementos : ^[43]

Si uno construye figuras similares (ver geometría euclidiana ) con lados correspondientes en los lados de un triángulo rectángulo, entonces la suma de las áreas de las que están en los dos lados más pequeños es igual al área de la que está en el lado mayor.

Esta extensión supone que los lados del triángulo original son los lados correspondientes de las tres figuras congruentes (por lo que las razones comunes de los lados entre las figuras similares son a:b:c ). ^[44] Si bien la prueba de Euclides solo se aplica a polígonos convexos, el teorema también se aplica a polígonos cóncavos e incluso a figuras similares que tienen límites curvos (pero aún con parte del límite de una figura siendo el lado del triángulo original). ^[44]

La idea básica detrás de esta generalización es que el área de una figura plana es proporcional al cuadrado de cualquier dimensión lineal y, en particular, es proporcional al cuadrado de la longitud de cualquier lado. Por lo tanto, si figuras similares con áreas A , B y C se erigen sobre lados con longitudes correspondientes a , b y c, entonces:

${\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,}$

${\displaystyle \Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,.}$

Pero, según el teorema de Pitágoras, a ² + b ² = c ² , entonces A + B = C .

Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a² + b² = c². (See also Einstein's proof by dissection without rearrangement)

Law of cosines

The separation s of two points (r₁, θ₁) and (r₂, θ₂) in polar coordinates is given by the law of cosines. Interior angle Δθ = θ₁−θ₂.

The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that

$${\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2}}$$

${\displaystyle \theta }$ ${\displaystyle a}$ ${\displaystyle b}$^[45]

When ${\displaystyle \theta }$ is ${\displaystyle {\frac {\pi }{2}}}$ radians or 90°, then ${\displaystyle \cos {\theta }=0}$, and the formula reduces to the usual Pythagorean theorem.

Arbitrary triangle

Generalization of Pythagoras' theorem by Tâbit ibn Qorra.^[46] Lower panel: reflection of triangle CAD (top) to form triangle DAC, similar to triangle ABC (top).

En cualquier ángulo seleccionado de un triángulo general de lados a, b, c , inscriba un triángulo isósceles tal que los ángulos iguales en su base θ sean los mismos que el ángulo seleccionado. Supongamos que el ángulo seleccionado θ está opuesto al lado etiquetado como c . Al inscribir el triángulo isósceles se forma el triángulo CAD con ángulo θ opuesto al lado by con lado r a lo largo de c . Se forma un segundo triángulo con un ángulo θ opuesto al lado a y un lado con longitud s a lo largo de c , como se muestra en la figura. Thābit ibn Qurra afirmó que los lados de los tres triángulos estaban relacionados como: ^{[47] [48]}

${\displaystyle a^{2}+b^{2}=c(r+s)\ .}$

A medida que el ángulo θ se acerca a π /2, la base del triángulo isósceles se estrecha y las longitudes r y s se superponen cada vez menos. Cuando θ = π /2, ADB se convierte en un triángulo rectángulo, r + s = c , y se recupera el teorema de Pitágoras original.

Una prueba observa que el triángulo ABC tiene los mismos ángulos que el triángulo CAD , pero en orden opuesto. (Los dos triángulos comparten el ángulo en el vértice A, ambos contienen el ángulo θ y, por lo tanto, también tienen el mismo tercer ángulo según el postulado del triángulo ). En consecuencia, ABC es similar a la reflexión de CAD , el triángulo DAC en el panel inferior. Tomando la relación de los lados opuestos y adyacentes a θ,

${\displaystyle {\frac {c}{b}}={\frac {b}{r}}\ .}$

Asimismo, para la reflexión del otro triángulo,

${\displaystyle {\frac {c}{a}}={\frac {a}{s}}\ .}$

Limpiando fracciones y sumando estas dos relaciones:

${\displaystyle cs+cr=a^{2}+b^{2}\ ,}$

el resultado requerido.

El teorema sigue siendo válido si el ángulo es obtuso, por lo que las longitudes r y s no se superponen. ${\displaystyle \theta }$

Triángulos generales usando paralelogramos.

Generalización para triángulos arbitrarios, área
verde = área azul

Construcción para prueba de generalización de paralelogramo.

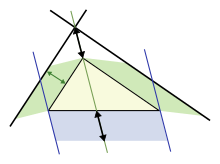
El teorema del área de Pappus es una generalización adicional, que se aplica a triángulos que no son triángulos rectángulos, utilizando paralelogramos en los tres lados en lugar de cuadrados (los cuadrados son un caso especial, por supuesto). La figura superior muestra que para un triángulo escaleno, el área del paralelogramo en el lado más largo es la suma de las áreas de los paralelogramos en los otros dos lados, siempre que el paralelogramo en el lado largo se construya como se indica (las dimensiones etiquetadas con Las flechas son iguales y determinan los lados del paralelogramo inferior). Esta sustitución de cuadrados por paralelogramos guarda un claro parecido con el teorema de Pitágoras original y fue considerada una generalización por Pappus de Alejandría en el año 4 d.C. ^{[49] [50]}

La figura inferior muestra los elementos de la prueba. Centrarse en el lado izquierdo de la figura. El paralelogramo verde izquierdo tiene la misma área que la porción azul izquierda del paralelogramo inferior porque ambos tienen la misma base by altura h . Sin embargo, el paralelogramo verde izquierdo también tiene la misma área que el paralelogramo verde izquierdo de la figura superior, porque tienen la misma base (el lado superior izquierdo del triángulo) y la misma altura normal a ese lado del triángulo. Repitiendo el argumento para el lado derecho de la figura, el paralelogramo inferior tiene la misma área que la suma de los dos paralelogramos verdes.

Geometria solida

El teorema de Pitágoras en tres dimensiones relaciona la diagonal AD con los tres lados.

Un tetraedro con una esquina en ángulo recto orientada hacia afuera.

En términos de geometría sólida , el teorema de Pitágoras se puede aplicar a tres dimensiones de la siguiente manera. Considere el cuboide que se muestra en la figura. La longitud de la diagonal de la cara AC se encuentra a partir del teorema de Pitágoras como:

${\displaystyle {\overline {AC}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BC}}^{\,2}\,,}$

donde estos tres lados forman un triángulo rectángulo. Usando la diagonal AC y el borde horizontal CD , la longitud de la diagonal del cuerpo AD se encuentra mediante una segunda aplicación del teorema de Pitágoras como:

${\displaystyle {\overline {AD}}^{\,2}={\overline {AC}}^{\,2}+{\overline {CD}}^{\,2}\,,}$

o hacerlo todo en un solo paso:

${\displaystyle {\overline {AD}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BC}}^{\,2}+{\overline {CD}}^{\,2}\,.}$

Este resultado es la expresión tridimensional de la magnitud de un vector v (la diagonal AD) en términos de sus componentes ortogonales { v _k } (los tres lados mutuamente perpendiculares):

${\displaystyle \|\mathbf {v} \|^{2}=\sum _{k=1}^{3}\|\mathbf {v} _{k}\|^{2}.}$

Esta formulación de un solo paso puede verse como una generalización del teorema de Pitágoras a dimensiones superiores. Sin embargo, este resultado es en realidad sólo la aplicación repetida del teorema de Pitágoras original a una sucesión de triángulos rectángulos en una secuencia de planos ortogonales.

Una generalización sustancial del teorema de Pitágoras a tres dimensiones es el teorema de Gua , llamado así por Jean Paul de Gua de Malves : si un tetraedro tiene una esquina en ángulo recto (como la esquina de un cubo ), entonces el cuadrado del área de la cara opuesta a la esquina del ángulo recto está la suma de los cuadrados de las áreas de las otras tres caras. Este resultado puede generalizarse como en el " teorema de Pitágoras n -dimensional": ^[51]

Sean vectores ortogonales en R ⁿ . Considere el simplex n -dimensional S con vértices . (Piense en el  símplex ( n − 1) dimensional con vértices que no incluyen el origen como la "hipotenusa" de S y las  caras restantes ( n − 1) dimensionales de S como sus "catetos".) Entonces el cuadrado del El volumen de la hipotenusa de S es la suma de los cuadrados de los volúmenes de los n catetos. ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$ ${\displaystyle 0,x_{1},\ldots ,x_{n}}$ ${\displaystyle x_{1},\ldots ,x_{n}}$

Esta afirmación se ilustra en tres dimensiones mediante el tetraedro de la figura. La "hipotenusa" es la base del tetraedro en la parte posterior de la figura, y los "patas" son los tres lados que emanan del vértice en primer plano. A medida que aumenta la profundidad de la base desde el vértice, el área de las "patas" aumenta, mientras que la de la base es fija. El teorema sugiere que cuando esta profundidad tiene el valor que crea un vértice recto, se aplica la generalización del teorema de Pitágoras. En una redacción diferente: ^[52]

Dado un simplex n -rectangular n -dimensional, el cuadrado del contenido ( n  − 1 ) de la faceta opuesta al vértice derecho será igual a la suma de los cuadrados de los contenidos ( n  − 1 ) de las facetas restantes.

Espacios interiores de productos

Vectores involucrados en la ley del paralelogramo.

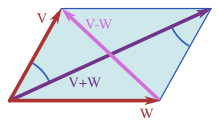
El teorema de Pitágoras se puede generalizar a espacios de productos internos , ^{[53] que son generalizaciones de los familiares} espacios euclidianos bidimensionales y tridimensionales . Por ejemplo, una función puede considerarse como un vector con infinitos componentes en un espacio producto interno, como en el análisis funcional . ^[54]

En un espacio producto interno, el concepto de perpendicularidad se reemplaza por el concepto de ortogonalidad : dos vectores v y w son ortogonales si su producto interno es cero. El producto interno es una generalización del producto escalar de vectores. El producto escalar se llama producto interno estándar o producto interno euclidiano . Sin embargo, son posibles otros productos interiores. ^[55] ${\displaystyle \langle \mathbf {v} ,\mathbf {w} \rangle }$

El concepto de longitud es sustituido por el concepto de norma ‖ v ‖ de un vector v , definida como: ^[56]

${\displaystyle \lVert \mathbf {v} \rVert \equiv {\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}\,.}$

En un espacio de producto interno, el teorema de Pitágoras establece que para dos vectores ortogonales cualesquiera v y w tenemos

${\displaystyle \left\|\mathbf {v} +\mathbf {w} \right\|^{2}=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2}.}$

Aquí los vectores v y w son similares a los lados de un triángulo rectángulo con hipotenusa dada por la suma vectorial v  +  w . Esta forma del teorema de Pitágoras es consecuencia de las propiedades del producto interno :

${\displaystyle {\begin{aligned}\left\|\mathbf {v} +\mathbf {w} \right\|^{2}&=\langle \mathbf {v+w} ,\ \mathbf {v+w} \rangle \\[3mu]&=\langle \mathbf {v} ,\ \mathbf {v} \rangle +\langle \mathbf {w} ,\ \mathbf {w} \rangle +\langle \mathbf {v,\ w} \rangle +\langle \mathbf {w,\ v} \rangle \\[3mu]&=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2},\end{aligned}}}$

donde debido a la ortogonalidad. ${\displaystyle \langle \mathbf {v,\ w} \rangle =\langle \mathbf {w,\ v} \rangle =0}$

Una generalización adicional del teorema de Pitágoras en un espacio producto interno para vectores no ortogonales es la ley del paralelogramo : ^[56]

${\displaystyle 2\|\mathbf {v} \|^{2}+2\|\mathbf {w} \|^{2}=\|\mathbf {v+w} \|^{2}+\|\mathbf {v-w} \|^{2}\ ,}$

que dice que el doble de la suma de los cuadrados de las longitudes de los lados de un paralelogramo es la suma de los cuadrados de las longitudes de las diagonales. Cualquier norma que satisfaga esta igualdad es ipso facto una norma correspondiente a un producto interno. ^[56]

La identidad pitagórica se puede extender a sumas de más de dos vectores ortogonales. Si v ₁ , v ₂ , ..., v _n son vectores ortogonales por pares en un espacio de producto interno, entonces la aplicación del teorema de Pitágoras a pares sucesivos de estos vectores (como se describe para 3 dimensiones en la sección sobre geometría sólida ) da como resultado la ecuación ^[57]

${\displaystyle {\biggl \|}\sum _{k=1}^{n}\mathbf {v} _{k}{\biggr \|}^{2}=\sum _{k=1}^{n}\|\mathbf {v} _{k}\|^{2}}$

Conjuntos de objetos m -dimensionales en un espacio n -dimensional

Otra generalización del teorema de Pitágoras se aplica a conjuntos de objetos mensurables según Lebesgue en cualquier número de dimensiones. Específicamente, el cuadrado de la medida de un conjunto de objetos de dimensiones m en uno o más planos paralelos de dimensiones m en un espacio euclidiano de dimensiones n es igual a la suma de los cuadrados de las medidas de las proyecciones ortogonales de los objetos. ) en todos los subespacios de coordenadas m -dimensionales. ^[58]

En términos matemáticos:

${\displaystyle \mu _{ms}^{2}=\sum _{i=1}^{x}\mathbf {\mu ^{2}} _{mp_{i}}}$

dónde:

• ${\displaystyle \mu _{m}}$es una medida en m -dimensiones (una longitud en una dimensión, un área en dos dimensiones, un volumen en tres dimensiones, etc.).
• ${\displaystyle s}$es un conjunto de uno o más objetos m -dimensionales que no se superponen en uno o más planos paralelos m -dimensionales en un espacio euclidiano n -dimensional.
• ${\displaystyle \mu _{ms}}$es la medida total (suma) del conjunto de m objetos dimensionales.
• ${\displaystyle p}$representa una proyección m -dimensional del conjunto original sobre un subespacio de coordenadas ortogonales.
• ${\displaystyle \mu _{mp_{i}}}$es la medida de la proyección del conjunto m -dimensional sobre el subespacio de coordenadas m -dimensional . Debido a que las proyecciones de objetos pueden superponerse en un subespacio de coordenadas, la medida de cada proyección de objetos en el conjunto debe calcularse individualmente, luego las medidas de todas las proyecciones se suman para proporcionar la medida total para el conjunto de proyecciones en el subespacio de coordenadas dado. ${\displaystyle i}$
• ${\displaystyle x}$es el número de subespacios de coordenadas ortogonales de m dimensiones en un espacio de n dimensiones ( R ⁿ ) sobre el cual se proyectan los objetos de m dimensiones ( m ≤ n ):
  $${\displaystyle x={\binom {n}{m}}={\frac {n!}{m!(n-m)!}}}$$

Geometría no euclidiana

El teorema de Pitágoras se deriva de los axiomas de la geometría euclidiana y, de hecho, si el teorema de Pitágoras fallara en algún triángulo rectángulo, entonces el plano en el que está contenido ese triángulo no puede ser euclidiano. Más precisamente, el teorema de Pitágoras implica, y está implícito en, el (quinto) postulado del paralelo de Euclides . ^{[59] [60]} Por lo tanto, los triángulos rectángulos en una geometría no euclidiana ^[61] no satisfacen el teorema de Pitágoras. Por ejemplo, en geometría esférica , los tres lados del triángulo rectángulo (digamos a , b y c ) que limitan un octante de la esfera unitaria tienen una longitud igual a π /2, y todos sus ángulos son rectos, lo que viola la regla pitagórica. teorema porque . ${\displaystyle a^{2}+b^{2}=2c^{2}>c^{2}}$

Aquí se consideran dos casos de geometría no euclidiana: la geometría esférica y la geometría plana hiperbólica ; en cada caso, como en el caso euclidiano de los triángulos no rectángulos, el resultado que reemplaza al teorema de Pitágoras se deriva de la ley apropiada de los cosenos.

Sin embargo, el teorema de Pitágoras sigue siendo válido en geometría hiperbólica y geometría elíptica si la condición de que el triángulo sea recto se reemplaza por la condición de que dos de los ángulos sumen el tercero, digamos A + B = C. Luego, los lados se relacionan de la siguiente manera: la suma de las áreas de los círculos con diámetros a y b es igual al área del círculo con diámetro c . ^[62]

Geometría esférica

Triángulo esférico

Para cualquier triángulo rectángulo en una esfera de radio R (por ejemplo, si γ en la figura es un ángulo recto), con lados a , b , c , la relación entre los lados toma la forma: ^[63]

${\displaystyle \cos {\frac {c}{R}}=\cos {\frac {a}{R}}\,\cos {\frac {b}{R}}.}$

Esta ecuación se puede derivar como un caso especial de la ley esférica de los cosenos que se aplica a todos los triángulos esféricos:

${\displaystyle \cos {\frac {c}{R}}=\cos {\frac {a}{R}}\,\cos {\frac {b}{R}}+\sin {\frac {a}{R}}\,\sin {\frac {b}{R}}\,\cos {\gamma }.}$

Para triángulos infinitesimales en la esfera (o equivalentemente, para triángulos esféricos finitos en una esfera de radio infinito), la relación esférica entre los lados de un triángulo rectángulo se reduce a la forma euclidiana del teorema de Pitágoras. Para ver cómo, supongamos que tenemos un triángulo esférico de longitudes laterales fijas a , b y c en una esfera con radio en expansión R. A medida que R se acerca al infinito , las cantidades a/R , b/R y c/R tienden a cero y la identidad pitagórica esférica se reduce a, por lo que debemos observar su expansión asintótica . ${\displaystyle 1=1,}$

La serie de Maclaurin para la función coseno se puede escribir como con el término restante en notación O grande . Dejando ser un lado del triángulo y tratando la expresión como una expansión asintótica en términos de R para una c fija , ${\textstyle \cos x=1-{\tfrac {1}{2}}x^{2}+O{\left(x^{4}\right)}}$ ${\displaystyle x=c/R}$

${\displaystyle {\begin{aligned}\cos {\frac {c}{R}}=1-{\frac {c^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}\end{aligned}}}$

y lo mismo para a y b . Sustituyendo la expansión asintótica de cada uno de los cosenos en la relación esférica de un triángulo rectángulo se obtiene

${\displaystyle {\begin{aligned}1-{\frac {c^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}&=\left(1-{\frac {a^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}\right)\left(1-{\frac {b^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}\right)\\&=1-{\frac {a^{2}}{2R^{2}}}-{\frac {b^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}.\end{aligned}}}$

Restando 1 y luego negando cada lado,

${\displaystyle {\frac {c^{2}}{2R^{2}}}={\frac {a^{2}}{2R^{2}}}+{\frac {b^{2}}{2R^{2}}}+O{\left(R^{-4}\right)}.}$

Multiplicando por 2 R ² , la expansión asintótica para c en términos de a , b fijo y R variable es

${\displaystyle c^{2}=a^{2}+b^{2}+O{\left(R^{-2}\right)}.}$

La relación euclidiana pitagórica se recupera en el límite, ya que el resto se desvanece cuando el radio R se acerca al infinito. ${\textstyle c^{2}=a^{2}+b^{2}}$

Para cálculos prácticos en trigonometría esférica con triángulos rectángulos pequeños, los cosenos se pueden reemplazar por senos usando la identidad de doble ángulo para evitar la pérdida de importancia . Entonces, el teorema de Pitágoras esférico se puede escribir alternativamente como ${\displaystyle \cos {2\theta }=1-2\sin ^{2}{\theta }}$

${\displaystyle \sin ^{2}{\frac {c}{2R}}=\sin ^{2}{\frac {a}{2R}}+\sin ^{2}{\frac {b}{2R}}-2\sin ^{2}{\frac {a}{2R}}\,\sin ^{2}{\frac {b}{2R}}.}$

Geometría hiperbólica

Triángulo hiperbólico

En un espacio hiperbólico con curvatura gaussiana uniforme −1/ R ^{2 , para un} triángulo rectángulo con catetos a , b e hipotenusa c , la relación entre los lados toma la forma: ^[64]

${\displaystyle \cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\,\cosh {\frac {b}{R}}}$

donde cosh es el coseno hiperbólico . Esta fórmula es una forma especial de la ley hiperbólica de los cosenos que se aplica a todos los triángulos hiperbólicos: ^[65]

${\displaystyle \cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\ \cosh {\frac {b}{R}}-\sinh {\frac {a}{R}}\ \sinh {\frac {b}{R}}\ \cos \gamma \ ,}$

con γ el ángulo en el vértice opuesto al lado c .

Al utilizar la serie de Maclaurin para el coseno hiperbólico, cosh x ≈ 1 + x ² /2 , se puede demostrar que cuando un triángulo hiperbólico se vuelve muy pequeño (es decir, cuando a , b y c se aproximan a cero), el coseno hiperbólico La relación para un triángulo rectángulo se acerca a la forma del teorema de Pitágoras.

Para triángulos rectángulos pequeños ( a , b << R ), los cosenos hiperbólicos se pueden eliminar para evitar la pérdida de significancia , dando

${\displaystyle \sinh ^{2}{\frac {c}{2R}}=\sinh ^{2}{\frac {a}{2R}}+\sinh ^{2}{\frac {b}{2R}}+2\sinh ^{2}{\frac {a}{2R}}\sinh ^{2}{\frac {b}{2R}}\,.}$

Triángulos muy pequeños

Para cualquier curvatura uniforme K (positiva, cero o negativa), en triángulos rectángulos muy pequeños (| K | a ² , | K | b ² << 1) con hipotenusa c , se puede demostrar que

${\displaystyle c^{2}=a^{2}+b^{2}-{\frac {K}{3}}a^{2}b^{2}-{\frac {K^{2}}{45}}a^{2}b^{2}(a^{2}+b^{2})-{\frac {2K^{3}}{945}}a^{2}b^{2}(a^{2}-b^{2})^{2}+O(K^{4}c^{10})\,.}$

Geometría diferencial

Distancia entre puntos infinitamente separados en coordenadas cartesianas (arriba) y coordenadas polares (abajo), según lo dado por el teorema de Pitágoras

El teorema de Pitágoras se aplica a los triángulos infinitesimales vistos en geometría diferencial . En el espacio tridimensional, la distancia entre dos puntos infinitamente separados satisface

${\displaystyle ds^{2}=dx^{2}+dy^{2}+dz^{2},}$

con ds el elemento de distancia y ( dx , dy , dz ) las componentes del vector que separa los dos puntos. Un espacio así se llama espacio euclidiano . Sin embargo, en geometría de Riemann , una generalización de esta expresión útil para coordenadas generales (no sólo cartesianas) y espacios generales (no sólo euclidianos) toma la forma: ^[66]

${\displaystyle ds^{2}=\sum _{i,j}^{n}g_{ij}\,dx_{i}\,dx_{j}}$

que se llama tensor métrico . (A veces, por abuso del lenguaje, se aplica el mismo término al conjunto de coeficientes g _ij .) Puede ser una función de la posición y, a menudo, describe un espacio curvo . Un ejemplo sencillo es el espacio euclidiano (plano) expresado en coordenadas curvilíneas . Por ejemplo, en coordenadas polares :

${\displaystyle ds^{2}=dr^{2}+r^{2}d\theta ^{2}\ .}$

Historia

La tablilla Plimpton 322 registra ternas pitagóricas de la época babilónica . ^[67]

Existe un debate sobre si el teorema de Pitágoras fue descubierto una vez o muchas veces en muchos lugares, y la fecha del primer descubrimiento es incierta, al igual que la fecha de la primera demostración. Los historiadores de las matemáticas mesopotámicas han llegado a la conclusión de que la regla pitagórica fue de uso generalizado durante el período de la antigua Babilonia (siglos XX al XVI a. C.), más de mil años antes del nacimiento de Pitágoras . ^{[68] [69] [70] [71]} La historia del teorema se puede dividir en cuatro partes: conocimiento de las ternas pitagóricas , conocimiento de la relación entre los lados de un triángulo rectángulo, conocimiento de las relaciones entre ángulos adyacentes y demostraciones del teorema dentro de algún sistema deductivo .

Escrito c. 1800  a. C., el Papiro de Berlín 6619 del Reino Medio egipcio incluye un problema cuya solución es el triple pitagórico 6:8:10, pero el problema no menciona un triángulo. La tablilla mesopotámica Plimpton 322 , escrita cerca de Larsa también c. 1800 a. C., contiene muchas entradas estrechamente relacionadas con las ternas pitagóricas. ^[72]  

En la India , el Baudhayana Shulba Sutra , cuyas fechas se dan de diversas formas entre los siglos VIII y V a. C., ^[73] contiene una lista de ternas pitagóricas y un enunciado del teorema de Pitágoras, ambos en el caso especial del derecho isósceles . triángulo y en el caso general, como lo hace el Apastamba Shulba Sutra ( c.  600 a. C. ). ^[a]

El filósofo y matemático neoplatónico bizantino Proclo , escribiendo en el siglo V d.C., establece dos reglas aritméticas, "una de ellas atribuida a Platón , la otra a Pitágoras", ^[75] para generar ternas pitagóricas especiales. La regla atribuida a Pitágoras ( c.  570  – c.  495 a. C. ) comienza a partir de un número impar y produce un triple con el cateto y la hipotenusa que difieren en una unidad; la regla atribuida a Platón (428/427 o 424/423 – 348/347 a. C.) comienza a partir de un número par y produce un triple con el cateto y la hipotenusa que difieren en dos unidades. Según Thomas L. Heath (1861-1940), no existe ninguna atribución específica del teorema a Pitágoras en la literatura griega superviviente de los cinco siglos posteriores a la vida de Pitágoras. ^[76] Sin embargo, cuando autores como Plutarco y Cicerón atribuyeron el teorema a Pitágoras, lo hicieron de una manera que sugiere que la atribución era ampliamente conocida e indudable. ^{[77] [78]} El clasicista Kurt von Fritz escribió: "Si esta fórmula se atribuye correctamente a Pitágoras personalmente... se puede asumir con seguridad que pertenece al período más antiguo de las matemáticas pitagóricas ". ^{[35] Alrededor del 300 a. C., en} los Elementos de Euclides , se presenta la prueba axiomática más antigua existente del teorema. ^[79]

Prueba geométrica del teorema de Pitágoras del Zhoubi Suanjing

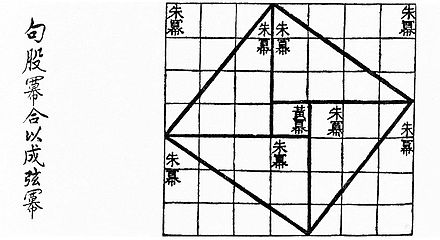
Con contenidos conocidos mucho antes, pero en textos supervivientes que datan aproximadamente del siglo I a.C., el texto chino Zhoubi Suanjing (周髀算经), ( El clásico aritmético del Gnomon y los senderos circulares del cielo ) da un razonamiento para el pitagórico. teorema del triángulo (3, 4, 5); en China se llama " teorema de Gougu " (勾股定理). ^{[80] [81]} Durante la dinastía Han (202 a. C. a 220 d. C.), los triples pitagóricos aparecen en Los nueve capítulos sobre el arte matemático , ^[82] junto con una mención de los triángulos rectángulos. ^[83] Algunos creen que el teorema surgió por primera vez en China en el siglo XI a. C., ^[84] donde también se lo conoce como " teorema de Shang Gao " (商高定理), ^[85] que lleva el nombre del astrónomo y matemático del duque de Zhou. , cuyo razonamiento compuso la mayor parte del contenido del Zhoubi Suanjing . ^[86]

Ver también

• Portal de matemáticas

• Suma en cuadratura
• En Dulcarnon
• Teorema de la bandera británica
• Silla de novia
• El último teorema de Fermat
• La demostración de Garfield del teorema de Pitágoras
• Hsuan jue
• Teorema de Pitágoras inverso
• triángulo de kepler
• Álgebra lineal
• Lista de temas triangulares
• espacio Lp^​
• número sin hipotenusa
• ley del paralelogramo
• La identidad de Parseval.
• teorema de ptolomeo
• Pitágoras en la cultura popular
• expectativa pitagórica
• mosaico pitagórico
• Trigonometría racional en el teorema de Pitágoras
• teorema de tales

notas y referencias

Notas

1. Van der Waerden creía que este material "ciertamente se basaba en tradiciones anteriores". Carl Boyer afirma que el teorema de Pitágoras en el Śulba-sũtram puede haber sido influenciado por las antiguas matemáticas mesopotámicas, pero no hay evidencia concluyente a favor o en contra de esta posibilidad. ^[74]

Referencias

1. Judith D. Sally; Paul Sally (2007). "Capítulo 3: Triples pitagóricos". Raíces de la investigación: un desarrollo vertical de los problemas matemáticos . Librería de la Sociedad Estadounidense de Matemáticas. pag. 63.ISBN​ 978-0-8218-4403-8.
2. Benson, Donald. El momento de la prueba: epifanías matemáticas , págs. 172-173 (Oxford University Press, 1999).
3. Euclides (1956), págs. 351–352
4. Huffman, Carl (23 de febrero de 2005). "Pitágoras". En Zalta, Edward N. (ed.). La Enciclopedia de Filosofía de Stanford (edición de invierno de 2018) ., "Ahora debería quedar claro que las decisiones sobre las fuentes son cruciales para abordar la cuestión de si Pitágoras era un matemático y un científico. La visión del cosmos de Pitágoras esbozada en los primeros cinco párrafos de esta sección, según la cual no era ni un matemático ni un científico, sigue siendo el consenso."
5. Alejandro Bogomolny. "Cut-the-knot.org: teorema de Pitágoras y sus numerosas pruebas, prueba n.º 4". Cortar el nudo . Consultado el 4 de noviembre de 2010 .
6. Alejandro Bogomolny. "Cut-the-knot.org: teorema de Pitágoras y sus numerosas pruebas, prueba n.º 3". Cortar el nudo . Consultado el 4 de noviembre de 2010 .
7. (Loomis 1940)
8. (Maor 2007, pag.39)
9. Schroeder, Manfred Robert (2012). Fractales, caos, leyes de poder: a minutos de un paraíso infinito . Corporación de mensajería. págs. 3–4. ISBN 978-0486134789.
10. Véase, por ejemplo, el teorema de Pitágoras mediante mapeo de corte. Archivado el 14 de octubre de 2016 en Wayback Machine , subprograma de Java del sitio web de la Universidad de Saint Louis.
11. Jan Gullberg (1997). Matemáticas: desde el nacimiento de los números . WW Norton & Company. pag. 435.ISBN​ 0-393-04002-X.
12. Heiberg, JL "Elementos de geometría de Euclides" (PDF) . págs. 46–47.
13. "Elementos de Euclides, Libro I, Proposición 47".Véase también una versión de la página web que utiliza subprogramas Java del Prof. David E. Joyce, Universidad Clark.
14. Stephen W. Hawking (2005). Dios creó los números enteros: los avances matemáticos que cambiaron la historia. Filadelfia: Editores de libros de Running Press. pag. 12.ISBN​ 0-7624-1922-9.Esta prueba apareció por primera vez después de que se configurara un programa de computadora para verificar las pruebas euclidianas.
15. La prueba de Pitágoras probablemente no fue general, ya que la teoría de las proporciones se desarrolló sólo dos siglos después de Pitágoras; ver (Maor 2007, p. 25)
16. Alejandro Bogomolny . "Teorema de Pitágoras, prueba número 10". Cortar el nudo . Consultado el 27 de febrero de 2010 .
17. (Loomis 1940, p. 113, prueba geométrica 22 y figura 123)
18. Polster, Burkard (2004). QED: Belleza en la prueba matemática . Compañía editorial Walker. pag. 49.
19. Publicado en una columna semanal de matemáticas: James A Garfield (1876). "Pons Asinorum". La Revista de Educación de Nueva Inglaterra . 3 (14): 161.como se señala en William Dunham (1997). El universo matemático: un viaje alfabético a través de las grandes pruebas, problemas y personalidades. Wiley. pag. 96.ISBN​ 0-471-17661-3.y en Un calendario de fechas matemáticas: 1 de abril de 1876 Archivado el 14 de julio de 2010 en Wayback Machine por V. Frederick Rickey.
20. Lantz, David. "La prueba de Garfield del teorema de Pitágoras". Math.Colgate.edu . Archivado desde el original el 28 de agosto de 2013 . Consultado el 14 de enero de 2018 .
21. Maor, Eli, El teorema de Pitágoras , Princeton University Press, 2007: págs.
22. Mike mirando (1996). "La proposición pitagórica: una prueba mediante el cálculo". Revista Matemáticas . Asociación Matemática de América. 69 (1): 45–46. doi :10.2307/2691395. JSTOR  2691395.
23. Bogomolny, Alejandro. "Teorema de pitágoras". Miscelánea interactiva de matemáticas y acertijos . Alejandro Bogomolny. Archivado desde el original el 6 de julio de 2010 . Consultado el 9 de mayo de 2010 .
24. Bruce C. Berndt (1988). "Ramanujan - ¿100 años (moderno) o 100 años nuevo (moderno)?". El inteligente matemático . 10 (3): 24–31. doi :10.1007/BF03026638. S2CID  123311054.
25. Judith D. Sally; Paul J. Sally Jr. (21 de diciembre de 2007). "Teorema 2.4 (Conversación del teorema de Pitágoras)". Raíces de la investigación . Sociedad Matemática Estadounidense . págs. 54–55. ISBN 978-0-8218-4403-8.
26. Elementos de Euclides, Libro I, Proposición 48 De la página web de DE Joyce en la Universidad de Clark
27. Casey, Stephen, "Lo inverso del teorema de Pitágoras", Mathematical Gazette 92, julio de 2008, 309–313.
28. Mitchell, Douglas W., "Comentarios sobre 92.47", Mathematical Gazette 93, marzo de 2009, 156.
29. Ernesto Julio Wilczynski; Masacre de Herbert Ellsworth (1914). "Teorema 1 y Teorema 2". Trigonometría plana y aplicaciones. Allyn y Bacon. pag. 85.
30. Dijkstra, Edsger W. (7 de septiembre de 1986). "Sobre el teorema de Pitágoras". EWD975 . Archivo EW Dijkstra.
31. Alexander Bogomolny, Teorema de Pitágoras para los recíprocos, https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
32. Ley, Henry (1853). "Corolario 5 de la Proposición XLVII (Teorema de Pitágoras)". Los elementos de Euclides: con muchas proposiciones adicionales y notas explicativas, a las que va precedido un ensayo introductorio a la lógica . Juan Weale. pag. 49.
33. Shaughan Lavine (1994). Entendiendo el infinito. Prensa de la Universidad de Harvard. pag. 13.ISBN​ 0-674-92096-1.
34. (Heath 1921, volumen I, págs.65); Hípaso estaba entonces de viaje y sus compañeros lo arrojaron por la borda. Véase James R. Choike (1980). "El pentagrama y el descubrimiento de un número irracional". La revista universitaria de matemáticas . 11 : 312–316.
35. Kurt Von Fritz (abril de 1945). "El descubrimiento de la inconmensurabilidad por Hipasus de Metapontum". Anales de Matemáticas . Segunda Serie. 46 (2): 242–264. doi :10.2307/1969021. JSTOR  1969021.
36. Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). "Distancia euclidiana". Dominio de algoritmos con Perl . O'Reilly Media, Inc. pág. 426.ISBN​ 1-56592-398-7.
37. Wentworth, George (2009). Trigonometría Plana y Tablas. BiblioBazaar, LLC. pag. 116.ISBN​ 978-1-103-07998-8., Ejercicios, página 116
38. Lawrence S. Leff (2005). Precálculo de forma sencilla (7ª ed.). Serie educativa de Barron. pag. 296.ISBN​ 0-7641-2892-2.
39. WS Massey (diciembre de 1983). "Productos cruzados de vectores en espacios euclidianos de dimensiones superiores" (PDF) . El Mensual Matemático Estadounidense . Asociación Matemática de América. 90 (10): 697–701. doi :10.2307/2323537. JSTOR  2323537. S2CID  43318100. Archivado desde el original (PDF) el 26 de febrero de 2021.
40. Pertti Lounesto (2001). "§7.4 Producto cruzado de dos vectores". Álgebras y espinores de Clifford (2ª ed.). Prensa de la Universidad de Cambridge. pag. 96.ISBN​ 0-521-00551-5.
41. Francis Begnaud Hildebrand (1992). Métodos de matemáticas aplicadas (Reimpresión de Prentice-Hall 1965, 2ª ed.). Publicaciones de Courier Dover. pag. 24.ISBN​ 0-486-67002-3.
42. Heath, TL, Una historia de las matemáticas griegas , Oxford University Press, 1921; reimpreso por Dover, 1981.
43. Elementos de Euclides : Libro VI, Proposición VI 31: "En los triángulos rectángulos, la figura del lado que subtiende el ángulo recto es igual a las figuras similares y descritas de manera similar en los lados que contienen el ángulo recto".
44. Putz, John F. y Sipka, Timothy A. "Sobre la generalización del teorema de Pitágoras", The College Mathematics Journal 34 (4), septiembre de 2003, págs.
45. Lawrence S. Leff (1 de mayo de 2005). obra citada. Serie educativa de Barron. pag. 326.ISBN​ 0-7641-2892-2.
46. Howard Whitley Evas (1983). "§4.8:... generalización del teorema de Pitágoras". Grandes momentos de las matemáticas (antes de 1650) . Asociación Matemática de América. pag. 41.ISBN​ 0-88385-310-8.
47. Aydin Sayili (marzo de 1960). "Generalización del teorema de Pitágoras de Thâbit ibn Qurra". Isis . 51 (1): 35–37. doi :10.1086/348837. JSTOR  227603. S2CID  119868978.
48. Judith D. Sally; Paul Sally (21 de diciembre de 2007). "Ejercicio 2.10 (ii)". Las raíces de la investigación: un desarrollo vertical de problemas matemáticos . Sociedad Matemática Estadounidense. pag. 62.ISBN​ 978-0-8218-4403-8.
49. Para conocer los detalles de dicha construcción, consulte Jennings, George (1997). "Figura 1.32: El teorema de Pitágoras generalizado". Geometría moderna con aplicaciones: con 150 figuras (3ª ed.). Saltador. pag. 23.ISBN​ 0-387-94222-X.
50. Claudi Alsina, Roger B. Nelsen: Pruebas encantadoras: un viaje a las matemáticas elegantes . MAA, 2010, ISBN 9780883853481 , págs. 77–78 ( extracto , pág. 77, en Google Books ) 
51. Rajendra Bhatia (1997). Análisis matricial. Saltador. pag. 21.ISBN​ 0-387-94846-5.
52. Para una discusión más amplia sobre esta generalización, consulte, por ejemplo, Willie W. Wong Archivado el 29 de diciembre de 2009 en Wayback Machine 2002, Un teorema de Pitágoras n-dimensional generalizado .
53. Fernando van der Heijden; Dick de Ridder (2004). Clasificación, estimación de parámetros y estimación de estado. Wiley. pag. 357.ISBN​ 0-470-09013-8.
54. Qun Lin; Jiafu Lin (2006). Métodos de elementos finitos: precisión y mejora. Elsevier. pag. 23.ISBN​ 7-03-016656-6.
55. Howard Antón; Chris Rorres (2010). Álgebra lineal elemental: versión de aplicaciones (10ª ed.). Wiley. pag. 336.ISBN​ 978-0-470-43205-1.
56. Karen Saxe (2002). "Teorema 1.2". Inicio del análisis funcional . Saltador. pag. 7.ISBN​ 0-387-95224-1.
57. Douglas, Ronald G. (1998). Técnicas de álgebra de Banach en la teoría del operador (2ª ed.). Nueva York, Nueva York: Springer-Verlag New York, Inc. págs. 60–61. ISBN 978-0-387-98377-6.
58. Donald R Conant y William A Beyer (marzo de 1974). "Teorema de Pitágoras generalizado". El Mensual Matemático Estadounidense . Asociación Matemática de América. 81 (3): 262–265. doi :10.2307/2319528. JSTOR  2319528.
59. Eric W. Weisstein (2003). Enciclopedia concisa de matemáticas CRC (2ª ed.). Prensa CRC. pag. 2147.ISBN​ 1-58488-347-2. El postulado de las paralelas es equivalente al postulado de la Equidistancia , al axioma de Playfair , al axioma de Proclo , al postulado del Triángulo y al teorema de Pitágoras .
60. Alexander R. Pruss (2006). El principio de razón suficiente: una reevaluación. Prensa de la Universidad de Cambridge. pag. 11.ISBN​ 0-521-85959-X. Podríamos incluir... el postulado de las paralelas y derivar el teorema de Pitágoras. O, en cambio, podríamos formular el teorema de Pitágoras entre los demás axiomas y derivar el postulado de las paralelas.
61. Stephen W. Hawking (2005). obra citada. Prensa corriente. pag. 4.ISBN​ 0-7624-1922-9.
62. Victor Pambuccian (diciembre de 2010). "Teorema de Pitágoras hiperbólico de María Teresa Calapso". El inteligente matemático . 32 (4): 2. doi : 10.1007/s00283-010-9169-0 .
63. Barrett O'Neill (2006). "Ejercicio 4". Geometría diferencial elemental (2ª ed.). Prensa académica. pag. 441.ISBN​ 0-12-088735-5.
64. Saúl Stahl (1993). "Teorema 8.3". El semiplano de Poincaré: una puerta de entrada a la geometría moderna . Aprendizaje de Jones y Bartlett. pag. 122.ISBN​ 0-86720-298-X.
65. Jane Gilman (1995). "Triángulos hiperbólicos". Subgrupos discretos de dos generadores de PSL(2,R) . Librería de la Sociedad Estadounidense de Matemáticas. ISBN 0-8218-0361-1.
66. Tai L. Chow (2000). Métodos matemáticos para físicos: una introducción concisa. Prensa de la Universidad de Cambridge. pag. 52.ISBN​ 0-521-65544-7.
67. Neugebauer 1969, pag. 36.
68. Neugebauer 1969: pág. 36 "En otras palabras, durante toda la matemática babilónica se sabía que la suma de los cuadrados de las longitudes de los lados de un triángulo rectángulo es igual al cuadrado de la longitud de la hipotenusa".
69. Friberg, Jöran (1981). "Métodos y tradiciones de las matemáticas babilónicas: Plimpton 322, ternas pitagóricas y ecuaciones de parámetros del triángulo babilónico". Historia Matemática . 8 : 277–318. doi : 10.1016/0315-0860(81)90069-0 .: pag. 306 "Aunque Plimpton 322 es un texto único en su tipo, hay varios otros textos conocidos que atestiguan que el teorema de Pitágoras era bien conocido por los matemáticos del período de la antigua Babilonia".
70. Hoyrup, Jens . "'Regla' y 'Teorema' de Pitágoras: espejo de la relación entre las matemáticas babilónicas y griegas". En Renger, Johannes (ed.). Babilonia: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Coloquio Internacional der Deutschen Orient-Gesellschaft 24.–26. Marzo de 1998 en Berlín (PDF) . Berlín: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. págs. 393–407., pag. 406, " A juzgar únicamente por esta evidencia, es probable que la regla pitagórica fuera descubierta dentro del entorno de los topógrafos legos, posiblemente como una consecuencia del problema tratado en Db ₂ -146, en algún momento entre 2300 y 1825 a. C.". ( Db _2-146 es una tablilla de arcilla de la antigua Babilonia de Eshnunna sobre el cálculo de los lados de un rectángulo dada su área y diagonal) .
71. Robson, E. (2008). Matemáticas en el antiguo Irak: una historia social . Prensa de la Universidad de Princeton.: pag. 109 "Muchos practicantes de matemáticas de la antigua Babilonia... sabían que el cuadrado en la diagonal de un triángulo rectángulo tenía la misma área que la suma de los cuadrados en el largo y el ancho: esa relación se usa en las soluciones elaboradas a problemas escritos sobre cortar y -pegar 'álgebra' en siete tablillas diferentes, de Ešnuna, Sippar, Susa y de un lugar desconocido en el sur de Babilonia."
72. Robson, Leonor (2001). "Ni Sherlock Holmes ni Babylon: una reevaluación de Plimpton 322". Historia Matemática . 28 (3): 167–206. doi : 10.1006/hmat.2001.2317 .
73. Kim Plofker (2009). Matemáticas en la India . Prensa de la Universidad de Princeton. págs. 17-18. ISBN 978-0-691-12067-6.
74. Carl Benjamín Boyer ; Uta C. Merzbach (2011). "China y la India". Una historia de las matemáticas (3ª ed.). Wiley. pag. 229.ISBN​ 978-0470525487. Cita: [En Sulba-sutras,] encontramos reglas para la construcción de ángulos rectos por medio de triples de cuerdas cuyas longitudes forman triajes pitagóricos, como 3, 4 y 5, o 5, 12 y 13, o 8, 15 y 17, o 12, 35 y 37. Aunque la influencia mesopotámica en los Sulvasũtras no es improbable, no conocemos ninguna evidencia concluyente a favor o en contra de esto. Aspastamba sabía que el cuadrado de la diagonal de un rectángulo es igual a la suma de los cuadrados de los dos lados adyacentes. Menos fácil de explicar es otra regla dada por Apastamba, una que se parece mucho al álgebra geométrica del Libro II de los Elementos de Euclides . (...)
75. Proclo (1970). Un comentario del primer libro de los elementos de Euclides. Traducido por Morrow, Glenn R. Princeton University Press. 428.6.
76. "Introducción y libros 1,2". La prensa universitaria. 25 de marzo de 1908 - vía Google Books.
77. (Heath 1921, Vol I, p. 144): "Aunque esta es la proposición universalmente asociada por tradición con el nombre de Pitágoras, no existe evidencia realmente confiable de que realmente fue descubierta por él. Los escritores comparativamente tardíos que lo atribuyen a él añade la historia de que sacrificó un buey para celebrar su descubrimiento".
78. Se proporciona una discusión extensa de la evidencia histórica en (Euclid 1956, p. 351) página = 351
79. Asger Aaboe (1997). Episodios de la historia temprana de las matemáticas. Asociación Matemática de América. pag. 51.ISBN​ 0-88385-613-1. ...no es hasta Euclides que encontramos una secuencia lógica de teoremas generales con demostraciones adecuadas.
80. Robert P. Crease (2008). Las grandes ecuaciones: avances científicos desde Pitágoras hasta Heisenberg. WW Norton & Co. pág. 25.ISBN​ 978-0-393-06204-5.
81. Christopher Cullen (2007) proporciona una discusión bastante extensa sobre los orígenes de los diversos textos del Zhou Bi . Astronomía y matemáticas en la antigua China: el 'Zhou Bi Suan Jing'. Prensa de la Universidad de Cambridge. págs. 139 y siguientes . ISBN 978-0-521-03537-8.
82. Esta obra es una recopilación de 246 problemas, algunos de los cuales sobrevivieron a la quema de libros del 213 a. C. y alcanzaron su forma final antes del 100 d. C. Liu Hui lo comentó extensamente en el año 263 d.C. Philip D. Straffin Jr. (2004). "Liu Hui y la primera edad de oro de las matemáticas chinas". En Marlow Anderson; Víctor J. Katz; Robin J. Wilson (eds.). Sherlock Holmes en Babilonia: y otros cuentos de la historia de las matemáticas . Asociación Matemática de América. págs. 69 y siguientes . ISBN 0-88385-546-1.Véase en particular §3: Nueve capítulos sobre el arte matemático , págs. 71 y siguientes .
83. Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). Los nueve capítulos sobre el arte matemático: acompañamiento y comentario. Prensa de la Universidad de Oxford. pag. 488.ISBN​ 0-19-853936-3.
84. En particular, Li Jimin; ver Centaurus, volumen 39. Copenhague: Munksgaard. 1997. págs.193, 205.
85. Chen, Cheng-Yih (1996). "§3.3.4 Fórmula de Chén Zǐ y método Chóng-Chã; Figura 40". Los primeros trabajos chinos en ciencias naturales: un reexamen de la física del movimiento, la acústica, la astronomía y el pensamiento científico . Prensa de la Universidad de Hong Kong. pag. 142.ISBN​ 962-209-385-X.
86. Wen-tsün Wu (2008). "El teorema de Gougu". Obras seleccionadas de Wen-tsün Wu . Científico mundial. pag. 158.ISBN​ 978-981-279-107-8.

Trabajos citados

• Bell, John L. (1999). El arte de lo inteligible: un estudio elemental de las matemáticas en su desarrollo conceptual. Kluwer. ISBN 0-7923-5972-0.
• Euclides (1956). Los trece libros de los elementos de Euclides, traducidos del texto de Heiberg, con introducción y comentario . vol. 1 (Libros I y II). Traducido por Heath, Thomas L. (Reimpresión de la segunda edición (1925)). Dover.Texto en línea en archive.org
• Brezo, señor Thomas (1921). "El 'teorema de Pitágoras'". Una historia de las matemáticas griegas (2 volúmenes) (Dover Publications, Inc. (1981) ed.). Prensa de Clarendon, Oxford. págs. 144 y siguientes . ISBN 0-486-24073-8.
• Libeskind, Shlomo (2008). Geometría euclidiana y transformacional: una investigación deductiva. Aprendizaje de Jones y Bartlett. ISBN 978-0-7637-4366-6.Este texto de geometría de la escuela secundaria cubre muchos de los temas de este artículo de WP.
• Loomis, Eliseo Scott (1940). La proposición pitagórica (2ª ed.). Ann Arbor, Michigan: hermanos Edwards. ISBN 9780873530361.Reeditado en 1968 por el Consejo Nacional de Profesores de Matemáticas. El Centro de información de recursos educativos , ERIC ED037335 , publicó en línea un escaneo de menor calidad .
• Maor, Eli (2007). El teorema de Pitágoras: una historia de 4.000 años. Princeton, Nueva Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
• Neugebauer, Otto (1969). Las ciencias exactas en la antigüedad. vol. 9 (Republicación de 1957 Brown University Press, 2ª ed.). Publicaciones de Courier Dover. págs. 1–191. ISBN 0-486-22332-9. OCLC  638685764. PMID  14884919. {{cite book}}: |journal=ignorado ( ayuda )
• Robson, Eleanor y Jacqueline Stedall, eds., The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, 2009. págs. vii + 918. ISBN 978-0-19-921312-2 . 
• Stillwell, John (1989). Matemáticas y su historia . Springer-Verlag. ISBN 0-387-96981-0.También ISBN 3-540-96981-0 . 
• Swetz, Frank; Kao, TI (1977). ¿Era chino Pitágoras?: Un examen de la teoría del triángulo rectángulo en la antigua China . Prensa de la Universidad Estatal de Pensilvania. ISBN 0-271-01238-2.
• van der Waerden, Bartel Leendert (1983). Geometría y Álgebra en las Civilizaciones Antiguas . Saltador. ISBN 3-540-12159-5. Triples pitagóricos de los escribas babilónicos van der Waerden.

enlaces externos

• Teorema de Pitágoras en ProofWiki

• Euclides (1997) [c. 300 aC]. David E. Joyce (ed.). Elementos . Consultado el 30 de agosto de 2006 .En HTML con figuras interactivas basadas en Java.
• "Teorema de pitágoras". Enciclopedia de Matemáticas . Prensa EMS . 2001 [1994].
• Tema de historia: el teorema de Pitágoras en las matemáticas babilónicas
• Enlaces interactivos:
  • Prueba interactiva en Java del teorema de Pitágoras
  • Otra prueba interactiva en Java del teorema de Pitágoras
  • Teorema de Pitágoras con animación interactiva
  • Teorema de Pitágoras animado, no algebraico y al ritmo del usuario
• Demostración del teorema de Pitágoras sobre el agua en YouTube
• Teorema de Pitágoras (más de 70 pruebas de cortar el nudo )
• Weisstein, Eric W. "Teorema de Pitágoras". MundoMatemático .