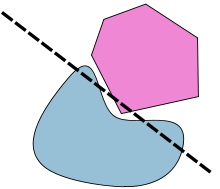
Teorema del hiperplano de separación
En geometría, el teorema del hiperplano de separación es un enunciado sobre formas convexas disjuntas en el espacio euclídeo de n dimensiones.
En una versión del teorema, si ambos conjuntos son disjuntos, cerrados y al menos uno de ellos es compacto, entonces existe un hiperplano entre ellos e incluso dos hiperplanos paralelos entre ellos separados por un espacio.
En otra versión, si ambos conjuntos convexos disjuntos están abiertos, entonces existe un hiperplano entre ellos, pero no necesariamente un espacio.
Por otro lado, el teorema de Hahn–Banach generaliza el resultado a espacios vectoriales topológicos.
dos subconjuntos convexos no vacíos disjuntos de
Si ambos conjuntos son cerrados y al menos uno de ellos es compacto, entonces la separación puede ser estricta, es decir,
son subconjuntos disjuntos, no vacíos y convexos de
En espacios de dimensión infinita hay ejemplos de dos conjuntos cerrados, convexos y disjuntos que no pueden separarse por un hiperplano cerrado (un hiperplano donde un funcional lineal continuo es igual a alguna constante), incluso en el sentido débil donde las desigualdades no son estrictas.
[4] Aquí no se puede relajar la hipótesis de compacidad; véase un ejemplo en la sección contraejemplos y unicidad.
La demostración se basa en el siguiente lema: Sean
(consúltese la página interior relativo para obtener más detalles).
Como la esfera unitaria es compacta, se puede tomar una subsecuencia convergente, de modo que
Dado que un hiperplano de separación no puede intersecar los interiores de conjuntos convexos abiertos, se deduce el corolario siguiente: Sean
Si ambos conjuntos son abiertos, entonces existe un vector
tienen posibles intersecciones, pero sus interiores relativos son disjuntos, entonces la prueba del primer caso aún se aplica sin cambios, lo que produce: Sean
tales que en particular, se tiene el hiperplano de soporte.
Si uno de los conjuntos A o B no es convexo, entonces hay muchos contraejemplos posibles.
Por ejemplo, A y B podrían ser círculos concéntricos.
Un contraejemplo más sutil es aquel en el que A y B son cerrados pero ninguno es compacto.
Por ejemplo, si A es un semiplano cerrado y B está delimitado por un brazo de una hipérbola, entonces no existe un hiperplano de separación estricta: (aunque, por un ejemplo del segundo teorema, existe un hiperplano que separa sus interiores).
En otro tipo de contraejemplo se tiene que A es compacto y B es abierto.
En la primera versión del teorema, evidentemente el hiperplano de separación nunca es único.
El ángulo abocinado proporciona un buen contraejemplo para muchas separaciones de hiperplanos.
, el disco unitario está separado del intervalo abierto
, pero la única recta que los separa contiene la totalidad de
está relativamente abierto, entonces no existe necesariamente una separación estricta para
está cerrado como politopo, entonces existe dicha separación.
Se pueden encontrar más resultados sobre conjuntos convexos disjuntos.
En 3D, el uso exclusivo de normales a las caras no logrará separar algunos casos de borde a borde que no colisionan.
[6] Para aumentar la eficiencia, los ejes paralelos se pueden calcular como un solo eje.