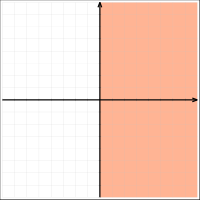
Semiplano
En geometría euclídea, una línea recta divide un plano en dos semiplanos.
denominados: Estas expresiones hacen referencia a semiplanos abiertos.
[2] Los matemáticos a veces identifican el plano cartesiano con el plano complejo, de forma que el semiplano superior corresponde al conjunto de números complejos con la parte imaginaria positiva: El término surge de una visualización común del número complejo x + iy como el punto (x, y) en el plano dotado de coordenadas cartesianas.
Cuando el eje y está orientado verticalmente, el "semiplano superior" corresponde a la región situada por encima del eje x y, es decir, a los números complejos para los que y > 0.
[3] El semiplano inferior, definido por y < 0, es igualmente útil, pero menos utilizado por convención.
(el conjunto de todos los números complejos de valor absoluto menor que uno) es equivalente por transformación conforme a
También juega un papel importante en geometría hiperbólica, donde el modelo del semiplano de Poincaré proporciona una forma de examinar el movimiento hiperbólico.
[5] El semiplano superior cerrado es la unión del semiplano superior y del eje real.
Las transformaciones afines del semiplano superior incluyen[6] Proposición: Sean A y B semicírculos en el semiplano superior con centros en el límite.
La distancia entre dos puntos cualesquiera p y q en el semiplano superior se puede definir consistentemente de la siguiente manera: el bisector perpendicular del segmento de p a q se cruza con el límite o es paralelo a él.
En el último caso, p y q se encuentran en un rayo perpendicular al límite y se puede utilizar un número positivo para definir una distancia que es invariante sometida a escalado.
En el primer caso, p y q se encuentran en un círculo centrado en la intersección de su bisectriz perpendicular y el límite.
Según la proposición anterior, este círculo se puede mover mediante un movimiento afín a
En consecuencia, el semiplano superior se convierte en un espacio métrico.
[7] El nombre genérico de este espacio métrico es geometría hiperbólica.
Una generalización natural en geometría diferencial es el n-espacio hiperbólico
el conjunto simplemente conexo de dimensión máxima simétrica, n, la variedad de Riemann con constante curvatura seccional −1.
[8] Con esta terminología, el semiplano superior es
de n copias del semiplano superior.