Potencial escalar
Un ejemplo familiar es energía potencial debida a la gravedad.
Un potencial escalar es un concepto fundamental en análisis vectorial y física (el adjetivo escalar se omite frecuentemente si no hay peligro de confusión con potencial vectorial).
Dado un campo vectorial F, el potencial escalar P se define tal que: donde ∇P es el gradiente de P y la segunda parte de la ecuación es menos el gradiente para una función del coordenadas cartesianas.
En algunos casos, los matemáticos pueden utilizar un signo positivo delante del gradiente para definir el potencial.
Para que F se describa sólo en términos de un potencial escalar, cualquiera de las siguientes afirmaciones equivalentes tiene que ser cierta:
donde la integración es sobre un Teorema de la curva de Jordan que pasa de la posición 'a a la posición b y P(b) es P evaluado en la posición b.
La primera de estas condiciones representa el teorema fundamental del gradiente y es cierta para cualquier campo vectorial que sea gradiente de una diferenciable.
monovaluada campo escalar P. La segunda condición es un requisito de F para que pueda expresarse como el gradiente de una función escalar.
La tercera condición re-expresa la segunda condición en términos del rotacional de F usando el teorema fundamental del rotacional.
Los potenciales escalares desempeñan un papel destacado en muchas áreas de la física y la ingeniería.
El potencial gravitatorio es el potencial escalar asociado a la gravedad por unidad de masa, es decir, la aceleración debida al campo, en función de la posición.
En electrostática el potencial eléctrico es el potencial escalar asociado al campo eléctrico, es decir, a la fuerza electrostática por unidad de carga.
En dinámica de fluidos, los campos laminares irrotacionales tienen un potencial escalar sólo en el caso especial en que se trata de un campo laplaciano.
El potencial juega un papel destacado en las formulaciones Lagrangiana y Hamiltoniana de la mecánica clásica.
Además, el potencial escalar es la cantidad fundamental en mecánica cuántica.
No todos los campos vectoriales tienen un potencial escalar.
Esto significa que la energía potencial gravitatoria en un mapa de contorno es proporcional a la altitud.
de modo que Sin embargo, en un mapa de contorno, el gradiente es inversamente proporcional a Δx, que no es similar a la fuerza FP: altitud en un mapa de contorno no es exactamente un campo potencial bidimensional.
En mecánica de fluidos, un fluido en equilibrio, pero en presencia de un campo gravitatorio uniforme está impregnado por una fuerza de flotación uniforme que anula la fuerza gravitatoria: así es como el fluido mantiene su equilibrio.
La presión en una masa de agua estática aumenta proporcionalmente a la profundidad por debajo de la superficie del agua.
Las superficies de presión constante son planos paralelos a la superficie, que puede caracterizarse como el plano de presión cero.
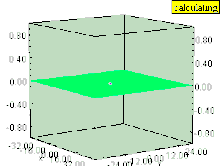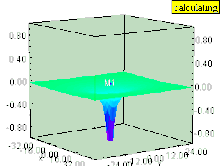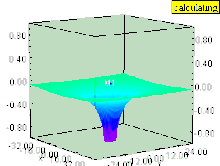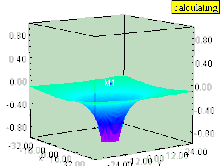
Si el líquido tiene un vórtice vertical (cuyo eje de rotación es perpendicular a la superficie), el vórtice provoca una depresión en el campo de presión.
La superficie del líquido dentro del vórtice es atraída hacia abajo, al igual que cualquier superficie de igual presión que permanezca paralela a la superficie del líquido.
La fuerza de flotación debida a un fluido sobre un objeto sólido sumergido y rodeado por ese fluido puede obtenerse integrando el gradiente negativo de presión a lo largo de la superficie del objeto: En el espacio euclídeo tridimensional, el potencial escalar de un campo vectorial conservativo o irrotacional, E está dado por
Esto se cumple siempre que E sea continua y desaparezca asintóticamente a cero hacia el infinito, decreciendo más rápido que 1/r y si la divergencia de E desaparece igualmente hacia el infinito, decreciendo más rápido que 1/r.F2.
Escrito de otra manera, dejemos que
Para un campo vectorial irrotacional G, se puede demostrar que
m a t h b f r
donde ω{sub}} es el volumen de la bola unitaria n. La demostración es idéntica.
Alternativamente, la integración por partes (o, más rigurosamente, la propiedades de la convolución) da