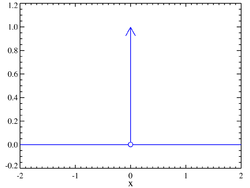
Delta de Dirac
Esta función constituye una aproximación muy útil para funciones picudas y constituye el mismo tipo de abstracción matemática que una carga o masa puntual.
En ocasiones se denomina también función de impulso.
La delta de Dirac es una función generalizada que viene definida por la siguiente fórmula integral: Donde f(x)= 1 (función constante) La delta de Dirac no es una función estrictamente hablando, puesto que se puede ver que requeriría tomar valores infinitos.
En términos del análisis dimensional, esta definición de
Se dice que una sucesión de funciones
es una función perteneciente a un espacio vectorial de funciones, y d es un funcional continuo del espacio vectorial dual (el conjunto de esos elementos continuos es un subespacio vectorial del dual, conocido como espacio dual topológico del espacio original de funciones.
La delta de Dirac centrada se puede definir como el límite distribucional del funcional dado por
e integrando teniendo en cuenta que la función delta no puede formar parte del resultado a menos que esté dentro de una integral.