Número práctico
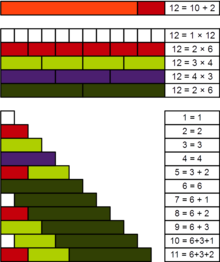
En teoría de números, un número práctico o número panarítmico[1] es un entero positivo n tal que todos los enteros positivos más pequeños pueden representarse como sumas de divisores distintos de n. Por ejemplo, 12 es un número práctico porque todos los números del 1 al 11 se pueden expresar como sumas sin repeticiones de sus divisores 1, 2, 3, 4 y 6: además de estos divisores, se tiene que 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1 y 11 = 6 + 3 + 2.
La secuencia de números prácticos (sucesión A005153 en OEIS) comienza así: Fibonacci utilizó números prácticos en su Liber Abaci (1202) en relación con el problema de representar números racionales como fracciones egipcias.
No definió formalmente los números prácticos, pero dio una tabla de expansiones de fracciones egipcias para fracciones con denominadores prácticos.
[2] El nombre "número práctico" se debe a Srinivasan (1948).
Esta caracterización permite determinar si un número es práctico al examinar su factorización prima.
También se ha demostrado que los números prácticos son análogos a los números primos en muchas de sus propiedades.
[3] La caracterización original deSrinivasan (1948) estableció que un número práctico no puede ser un número deficiente, uno cuya suma de todos los divisores (incluido 1 y sí mismo) es menos del doble del número, a menos que la deficiencia sea uno.
Si el conjunto ordenado de todos los divisores del número práctico
, entonces la declaración de Srinivasan se puede expresar por la desigualdad En otras palabras, la secuencia ordenada de todos los divisores.
de un número práctico tiene que ser una subsecuencia completa.
Esta caracterización parcial fue extendida y completada porStewart (1954) ySierpiński (1955) quienes demostraron que es sencillo determinar si un número es práctico a partir de su factorización prima.
Un entero positivo mayor que uno con factorización prima
tenga una representación como una suma de divisores más pequeños.
La condición indicada anteriormente es necesaria y suficiente para que un número sea práctico.
En una dirección, esta condición es necesaria para poder representar
como una suma de divisores de n, porque si la desigualdad no fuera cierta, incluso sumando todos los divisores más pequeños daría una suma demasiado pequeña para alcanzar
En la otra dirección, la condición es suficiente, como se puede demostrar por inducción.
Más concluyentemente, si la factorización de n satisface la condición anterior, entonces cualquier
puede representarse como una suma de divisores de n, mediante la siguiente secuencia de pasos:[4] Varios otros conjuntos notables de enteros consisten solo en números prácticos: Si n es práctico, entonces cualquier número racional de la forma m/n con m < n puede representarse como una suma ∑di/n donde cada di es un divisor distinto de n. Cada término en esta suma se simplifica a una fracción unitaria, por lo que dicha suma proporciona una representación de m/n como una fracción egipcia.
De estos, el primero es probar si el número ya es una fracción unitaria, pero el segundo es buscar una representación del numerador como una suma de divisores del denominador, como se describió anteriormente.
Este método solo tiene éxito para los denominadores que sean prácticos.
Fibonacci proporciona tablas de estas representaciones para fracciones que tienen como denominadores los números prácticos 6, 8, 12, 20, 24, 60 y 100.Vose (1985) demostró que cada número x/y tiene una representación de fracción egipcia con
La prueba consiste en encontrar una secuencia de números prácticos ni con la propiedad de que cada número menor que ni puede escribirse como una suma de
Entonces, se elige i para que ni − 1 < y ≤ ni, y además xni se divide entre y, dando el cociente q y el resto r. De estas elecciones se desprende que
[7] Una razón para interesarse en los números prácticos es que muchas de sus propiedades son similares a las propiedades de los números primos.
De hecho, los teoremas análogos a la conjetura de Goldbach y a la conjetura de primos gemelos son conocidas para los números prácticos: cada entero par positivo es la suma de dos números prácticos, y existen infinitos tripletes de números prácticos x − 2, x, x + 2.
[8] Melfi también demostró que hay infinitos números prácticos en la sucesión de Fibonacci (sucesión A124105 en OEIS).
La pregunta análoga de la existencia de infinitos primos de Fibonacci está abierta.Hausman y Shapiro (1984) demostraron que siempre existe un número práctico en el intervalo [x2, (x + 1)2] para cualquier x real positivo, un resultado análogo a la conjetura de Legendre para primos.
Este resultado en números prácticos en intervalos cortos ha sido mejorado posteriormente por Melfi, quien demostró[9] que si
es la secuencia de números prácticos, entonces para n suficientemente grande y para un A adecuado, Sea p(x) la cantidad de números prácticos que existen hasta alcanzar x.Margenstern (1991) conjeturó que p(x) es asintótico a cx/log x para alguna constante c, una fórmula que se asemeja al teorema de los números primos, lo que refuerza la afirmación anterior deErdős y Loxton (1979) de que los números prácticos tienen una densidad cero en los enteros.Saias (1997) demostró que, para constantes positivas adecuadas c 1 y c 2, Weingartner (2015) demostró la conjetura de Margenstern al comprobar que donde