Derivada parcial
Las derivadas parciales son usadas en cálculo vectorial y geometría diferencial.
La notación moderna de derivadas parciales fue creada por Adrien-Marie Legendre (1786), aunque más tarde la abandonó; Carl Gustav Jacob Jacobi reintrodujo el símbolo en 1841.
), es decir: Al realizar esta derivada obtenemos la expresión que nos permite calcular la pendiente de la recta tangente a dicha función
Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada con el eje que representa los valores de la función.
Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
La notación moderna de la derivada parcial fue creada por Adrien-Marie Legendre (1786), aunque posteriormente la abandonó; Carl Gustav Jacob Jacobi reintrodujo el símbolo en 1841.
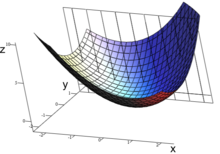
La gráfica de esta función define una superficie en el espacio euclidiano.
Para cada punto en esta superficie, hay un número infinito de líneas tangentes.
La gráfica de la función y este plano se muestran a la derecha.
A la izquierda, vemos cómo se ve la función en el plano
Sin embargo, si todas las derivadas parciales existen en un entorno de
Si todas las derivadas parciales mixtas de segundo orden son continuas en un punto, entonces
en ese punto; en tal caso, las derivadas parciales pueden ser intercambiadas por el teorema de Clairaut: El volumen
son respectivamente, la primera de ellas representa la tasa a la que el volumen del cono cambia si el radio varía y su altura se mantiene constante, la segunda de ellas representa la tasa a la que el volumen cambia si la altura varía y su radio se mantiene constante.
En este caso f tiene una derivada parcial ∂f/∂xj con respecto a cada variable xj.
: O, de manera más general, para el espacio euclidiano n-dimensional
: Considere una función Las derivadas parciales de primer orden respecto a la variable
suelen denotarse por Las derivadas parciales de segundo orden suelen denotarse por Las derivadas cruzadas de segundo orden por En termodinámica y otras áreas de la física se emplea la siguiente notación: que significa que
y entonces: Esta notación se usa porque frecuentemente una magnitud puede expresarse como función de diferentes variables por lo que en general: Ya que la forma precisa de las funciones
puede verse como otra función definida en U y derivarse parcialmente.
La derivada direccional de una función escalar f con respecto a un vector v en un punto (por ejemplo, posición) x puede ser denotada por cualquiera de los siguientes:
Por ejemplo, La gráfica de esta función define una superficie en el espacio euclídeo.
La diferenciación parcial consiste en elegir una de estas rectas y hallar su pendiente.
Normalmente, las rectas de mayor interés son las paralelas al plano
La gráfica y este plano se muestran a la derecha.
Una vez elegido un valor de y, digamos a, entonces f(x,y) determina una función fa que traza una curva x2 + ax + a2' en el plano
Aquí ∂ es una d redondeada llamada símbolo de derivada parcial'; para distinguirla de la letra d, ∂ a veces se pronuncia "parcial".
La derivada parcial cruzada con respecto a x e y se obtiene tomando la derivada parcial de f con respecto a x, y luego tomando la derivada parcial del resultado con respecto a y, para obtener Teorema de Schwarz afirma que si las segundas derivadas son continuas, la expresión para la derivada parcial cruzada no se ve afectada por qué variable se toma la derivada parcial respecto a la primera y cuál se toma respecto a la segunda.
Las derivadas parciales propias y cruzadas aparecen en la matriz hessiana que se utiliza en las condiciones de segundo ordens en problemas de optimización.
Si se conocen todas las derivadas parciales de una función (por ejemplo, con el gradiente), entonces las antiderivadas pueden emparejarse mediante el proceso anterior para reconstruir la función original hasta una constante.