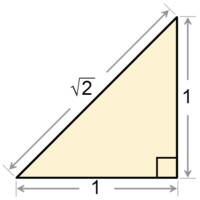
Raíz cuadrada de dos
La raíz cuadrada de 2 se define como el único número real positivo tal que, multiplicado por sí mismo, es igual a 2.
La notación tradicional, utilizando el símbolo de radicación es
La raíz cuadrada de 2 es un número irracional (más aún, es algebraico de grado 2), su valor numérico es aproximadamente 1,4, y truncado en 100 dígitos decimales se obtiene:[1]
La raíz cuadrada de 2 fue posiblemente el primer número irracional conocido.
[cita requerida] La raíz cuadrada de 2 no es un número racional.
en cuatro dígitos sexagesimales, que es similar a seis cifras decimales:[3] Otra aproximación antigua a este número irracional se da en la antigua India, en el texto matemático Baudhaiana-sulba-sutra (entre el 600 y el 300 a. C.), diciendo: incrementa la longitud (del lado) por su tercera parte, y su tercera por sus tres cuartas y su tercera por su treinta y cuatroava parte de cuatro.
Posteriormente, desde la visión algebraica, esta raíz cuadrada satisface la ecuación
La historia narra que precisamente descubrió la irracionalidad de la raíz de 2 cuando intentaba averiguar una expresión racional del mismo.
Sin embargo Pitágoras creía en la definición absoluta de los números como medida, y esto le obligaba a no creer en la existencia de los números irracionales.
Por esta razón, estando ya desde el principio en contra de esa demostración, sus compañeros pitagóricos sentenciaron a Hipaso a la pena capital, ahogándole en el mar.
Funciona como sigue: Se toma en primer lugar un valor arbitrario, que denominamos,
; esta primera aproximación importa poco, es considerada solo como un punto de comienzo del algoritmo y afecta en cuantas iteraciones debe hacer el algoritmo hasta alcanzar la aproximación con una precisión requerida.
Entonces, empleando esta suposición inicial, se procede a iterar mediante la siguiente cómputo recursivo: Cuanto más iteraciones se hagan mediante este algoritmo (es decir más cálculos con un valor de n grande), se obtendrá una mejor aproximación del valor real de raíz cuadrada de 2.
ha sido calculado hasta 137 438 953 444 posiciones decimales por el equipo de Yasumasa Kanada en el año 1997.
Entre las constantes matemáticas con cifras no periódicas, solo π ha sido calculado con mayor precisión.
basadas en el método del descenso infinito y en el método de reducción al absurdo, que se fundamenta en suponer que
Se fundamenta en el método del descenso infinito.
Es una construcción geométrica clásica de regla y compás, probando el teorema por un modo muy similar a como lo hacían los antiguos geómetras griegos.
son congruentes por tener dos lados iguales y el ángulo comprendido también.
es la mitad de un recto, BEF es también un triángulo rectángulo isósceles.
, que son números también enteros y menores a
dos triángulos semejantes podemos repetir el anterior proceso de forma recurrente.
son enteros debe existir una fracción irreducible.
son números enteros es falsa y que
mediante una sucesión infinita de intervalos encajados, los extremos inferiores forman una sucesión creciente estricta, tal que el siguiente tiene más cifras, como esto puede continuar indefinidamente, el número de cifras decimales, aumenta sin cesar, o es una infinidad.
, este conjunto es un abierto en la topología usual de la recta real y su clausura es
La raíz cuadrada es conocida también como una fracción continua La identidad
Sin embargo, si se conocen las fórmulas de tipo-BBP para π√2 y para √2 ln(1+√2).
El conjunto H = {a + b √2; a, b∈ℚ} provisto de la adición y la múltiplicación es un cuerpo, previamente
[12] Al número irracional a + b√2 se llama irracionalidad cuadrática,[13] porque junto con su conjugado a - b√2 son raíces de una ecuación algebraica de segundo grado.