Momento angular

Cantidad física conservada; análogo rotacional del momento lineal

En física , el momento angular (a veces llamado momento de impulso o momento de rotación ) es el análogo rotacional del momento lineal . Es una cantidad física importante porque es una cantidad conservada  : el momento angular total de un sistema cerrado permanece constante. El momento angular tiene dirección y magnitud, y ambas se conservan. Las bicicletas y motocicletas , los discos voladores , ^[1] las balas estriadas y los giroscopios deben sus útiles propiedades a la conservación del momento angular. La conservación del momento angular también es la razón por la que los huracanes ^[2] forman espirales y las estrellas de neutrones tienen altas velocidades de rotación. En general, la conservación limita el posible movimiento de un sistema, pero no lo determina de forma única.

El momento angular tridimensional de una partícula puntual se representa clásicamente como un pseudovector r × p , el producto cruzado del vector de posición de la partícula r (con respecto a algún origen) y su vector de momento ; este último es p = m v en la mecánica newtoniana . A diferencia del momento lineal, el momento angular depende de dónde se elige este origen, ya que a partir de él se mide la posición de la partícula.

El momento angular es una cantidad extensa ; es decir, el momento angular total de cualquier sistema compuesto es la suma de los momentos angulares de sus partes constituyentes. Para un cuerpo rígido continuo  o un fluido , el momento angular total es la integral de volumen de la densidad del momento angular (momento angular por unidad de volumen en el límite cuando el volumen se reduce a cero) sobre todo el cuerpo.

De manera similar a la conservación del momento lineal, donde se conserva si no hay una fuerza externa, el momento angular se conserva si no hay un par externo . El par se puede definir como la tasa de cambio del momento angular, análoga a la fuerza . El par externo neto en cualquier sistema es siempre igual al par total en el sistema; en otras palabras, la suma de todos los pares internos de cualquier sistema es siempre 0 (este es el análogo rotacional de la tercera ley del movimiento de Newton ). Por lo tanto, para un sistema cerrado (donde no hay par externo neto), el par total en el sistema debe ser 0, lo que significa que el momento angular total del sistema es constante.

El cambio en el momento angular para una interacción particular se llama impulso angular , a veces giro . ^[3] El impulso angular es el análogo angular del impulso (lineal) .

Ejemplos

El caso trivial del momento angular de un cuerpo en una órbita viene dado por ${\displaystyle L}$

$${\displaystyle L=2\pi Mfr^{2}}$$

masafrecuencia ${\displaystyle M}$ ${\displaystyle f}$ ${\displaystyle r}$

En cambio , el momento angular de una esfera rígida uniforme que gira alrededor de su eje viene dado por ${\displaystyle L}$

$${\displaystyle L={\frac {4}{5}}\pi Mfr^{2}}$$

donde es la masa de la esfera, es la frecuencia de rotación y es el radio de la esfera. ${\displaystyle M}$ ${\displaystyle f}$ ${\displaystyle r}$

Así, por ejemplo, el momento angular orbital de la Tierra con respecto al Sol es de aproximadamente 2,66 × 10 ⁴⁰ kg⋅m ² ⋅s ⁻¹ , mientras que su momento angular de rotación es de aproximadamente 7,05 × 10 ³³ kg⋅m ² ⋅s ^{− 1} .

En el caso de una esfera rígida uniforme que gira alrededor de su eje, si en lugar de su masa se conoce su densidad , el momento angular viene dado por ${\displaystyle L}$

$${\displaystyle L={\frac {16}{15}}\pi ^{2}\rho fr^{5}}$$

donde es la densidad de la esfera , es la frecuencia de rotación y es el radio de la esfera. ${\displaystyle \rho }$ ${\displaystyle f}$ ${\displaystyle r}$

En el caso más simple de un disco giratorio, el momento angular viene dado por ^[4] ${\displaystyle L}$

$${\displaystyle L=\pi Mfr^{2}}$$

donde es la masa del disco, es la frecuencia de rotación y es el radio del disco. ${\displaystyle M}$ ${\displaystyle f}$ ${\displaystyle r}$

Si, en cambio, el disco gira alrededor de su diámetro (por ejemplo, al lanzar una moneda), su momento angular viene dado por ^[4] ${\displaystyle L}$

$${\displaystyle L={\frac {1}{2}}\pi Mfr^{2}}$$

Definición en mecánica clásica.

Al igual que para la velocidad angular , existen dos tipos especiales de momento angular de un objeto: el momento angular de giro es el momento angular alrededor del centro de masa del objeto , mientras que el momento angular orbital es el momento angular alrededor de un centro de rotación elegido. La Tierra tiene un momento angular orbital por la naturaleza de girar alrededor del Sol , y un momento angular de giro por la naturaleza de su rotación diaria alrededor del eje polar. El momento angular total es la suma de los momentos angulares orbitales y de giro. En el caso de la Tierra, la principal cantidad conservada es el momento angular total del sistema solar porque el momento angular se intercambia en una medida pequeña pero importante entre los planetas y el Sol. El vector de momento angular orbital de una partícula puntual es siempre paralelo y directamente proporcional a su vector de velocidad angular orbital ω , donde la constante de proporcionalidad depende tanto de la masa de la partícula como de su distancia desde el origen. El vector de momento angular de giro de un cuerpo rígido es proporcional pero no siempre paralelo al vector de velocidad angular de giro Ω , lo que hace que la constante de proporcionalidad sea un tensor de segundo rango en lugar de un escalar.

Momento angular orbital en dos dimensiones.

La velocidad de la partícula m con respecto al origen O se puede resolver en componentes paralelas a ( v _∥ ) y perpendiculares a ( v _⊥ ) el radio vector r . El momento angular de m es proporcional a la componente perpendicular v _⊥ de la velocidad, o equivalentemente, a la distancia perpendicular r _⊥ desde el origen.

El momento angular es una cantidad vectorial (más precisamente, un pseudovector ) que representa el producto de la inercia rotacional de un cuerpo y la velocidad de rotación (en radianes/seg) alrededor de un eje particular. Sin embargo, si la trayectoria de la partícula se encuentra en un solo plano , es suficiente descartar la naturaleza vectorial del momento angular y tratarlo como un escalar (más precisamente, un pseudoescalar ). ^[5] El momento angular puede considerarse un análogo rotacional del momento lineal. Por lo tanto, donde el momento lineal p es proporcional a la masa m y la velocidad lineal v ,

pags = metro v , {\displaystyle p=mv,}

El momento angular L es proporcional al momento de inercia I y a la velocidad angular ω medida en radianes por segundo. ^[6]

L = yo ω . {\displaystyle L=I\omega .}

A diferencia de la masa, que depende únicamente de la cantidad de materia, el momento de inercia depende también de la posición del eje de rotación y de la distribución de la materia. A diferencia de la velocidad lineal, que no depende de la elección del origen, la velocidad angular orbital siempre se mide con respecto a un origen fijo. Por lo tanto, en sentido estricto, L debería denominarse momento angular relativo a ese centro . ^[7]

En el caso del movimiento circular de una sola partícula, podemos usar y para expandir el momento angular reduciéndolo a: ${\displaystyle I=r^{2}m}$ ${\displaystyle \omega ={v}/{r}}$ ${\displaystyle L=r^{2}m\cdot {v}/{r},}$

$${\displaystyle L=rmv,}$$

el producto del radio de rotación r y el momento lineal de la partícula , donde es la velocidad lineal (tangencial) . ${\displaystyle p=mv}$ ${\displaystyle v=r\omega }$

Este análisis simple también se puede aplicar al movimiento no circular si se usa la componente del movimiento perpendicular al vector radio :

$${\displaystyle L=rmv_{\perp },}$$

donde es la componente perpendicular del movimiento. Al expandirse, reorganizarse y reducirse, el momento angular también se puede expresar, ${\displaystyle v_{\perp }=v\sin(\theta )}$ ${\displaystyle L=rmv\sin(\theta ),}$ ${\displaystyle L=r\sin(\theta )mv,}$

$${\displaystyle L=r_{\perp }mv,}$$

¿Dónde está la longitud del brazo de momento , una línea que cae perpendicularmente desde el origen a la trayectoria de la partícula? Es esta definición, (longitud del brazo de momento) × (momento lineal) , a la que se refiere el término momento de momento . ^[8] ${\displaystyle r_{\perp }=r\sin(\theta )}$

Momento angular escalar de la mecánica lagrangiana

Otro enfoque consiste en definir el momento angular como el momento conjugado (también llamado momento canónico ) de la coordenada angular expresada en el lagrangiano del sistema mecánico. Considere un sistema mecánico con una masa obligada a moverse en un círculo de radio en ausencia de cualquier campo de fuerza externo. La energía cinética del sistema es ${\displaystyle \phi }$ ${\displaystyle m}$ ${\displaystyle r}$

T = 1 2 metro r 2 ω 2 = 1 2 metro r 2 ϕ ˙ 2 . {\displaystyle T={\tfrac {1}{2}}señor^{2}\omega ^{2}={\tfrac {1}{2}}señor^{2}{\dot {\phi }} ^{2}.}

Y la energía potencial es

$${\displaystyle U=0.}$$

Entonces el lagrangiano es

$${\displaystyle {\mathcal {L}}\left(\phi ,{\dot {\phi }}\right)=T-U={\tfrac {1}{2}}mr^{2}{\dot {\phi }}^{2}.}$$

El impulso generalizado "canónicamente conjugado con" la coordenada se define por ${\displaystyle \phi }$

$${\displaystyle p_{\phi }={\frac {\partial {\mathcal {L}}}{\partial {\dot {\phi }}}}=mr^{2}{\dot {\phi }}=I\omega =L.}$$

Momento angular orbital en tres dimensiones.

Relación entre los vectores fuerza ( F ), par ( τ ), momento ( p ) y momento angular ( L ) en un sistema giratorio. r es el vector de posición .

Para definir completamente el momento angular orbital en tres dimensiones , se requiere conocer la velocidad a la que el vector de posición barre el ángulo, la dirección perpendicular al plano instantáneo de desplazamiento angular y la masa involucrada, así como cómo se distribuye esta masa. en el espacio. ^[9] Al conservar esta naturaleza vectorial del momento angular, también se conserva la naturaleza general de las ecuaciones y puede describir cualquier tipo de movimiento tridimensional alrededor del centro de rotación: circular , lineal o de otro tipo. En notación vectorial , el momento angular orbital de una partícula puntual en movimiento alrededor del origen se puede expresar como:

$${\displaystyle \mathbf {L} =I{\boldsymbol {\omega }},}$$

• ${\displaystyle I=r^{2}m}$es el momento de inercia de una masa puntual ,
• ω = r × v r 2 {\displaystyle {\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}} es la velocidad angular orbital de la partícula sobre el origen,
• ${\displaystyle \mathbf {r} }$es el vector de posición de la partícula con respecto al origen, y , ${\displaystyle r=\left\vert \mathbf {r} \right\vert }$
• ${\displaystyle \mathbf {v} }$es la velocidad lineal de la partícula con respecto al origen, y
• ${\displaystyle m}$es la masa de la partícula.

Esto se puede ampliar, reducir y, según las reglas del álgebra vectorial , reorganizar:

$${\displaystyle {\begin{aligned}\mathbf {L} &=\left(r^{2}m\right)\left({\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}\right)\\&=m\left(\mathbf {r} \times \mathbf {v} \right)\\&=\mathbf {r} \times m\mathbf {v} \\&=\mathbf {r} \times \mathbf {p} ,\end{aligned}}}$$

producto cruzadoperpendicularregla de la mano derechasentido contrario a las agujas del relojplano ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {p} =m\mathbf {v} }$ ${\displaystyle \mathbf {L} }$ ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {p} }$ ${\displaystyle \mathbf {L} }$ ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {p} }$

Al definir un vector unitario perpendicular al plano de desplazamiento angular, se obtiene una velocidad angular escalar , donde ${\displaystyle \mathbf {\hat {u}} }$ ${\displaystyle \omega }$

$${\displaystyle \omega \mathbf {\hat {u}} ={\boldsymbol {\omega }},}$$

$${\displaystyle \omega ={\frac {v_{\perp }}{r}},}$$

${\displaystyle v_{\perp }}$

Por lo tanto, se puede dar dirección a las ecuaciones escalares bidimensionales de la sección anterior:

$${\displaystyle {\begin{aligned}\mathbf {L} &=I{\boldsymbol {\omega }}\\&=I\omega \mathbf {\hat {u}} \\&=\left(r^{2}m\right)\omega \mathbf {\hat {u}} \\&=rmv_{\perp }\mathbf {\hat {u}} \\&=r_{\perp }mv\mathbf {\hat {u}} ,\end{aligned}}}$$

${\displaystyle \mathbf {L} =rmv\mathbf {\hat {u}} }$ ${\displaystyle r}$

En el sistema de coordenadas esféricas el vector de momento angular se expresa como

${\displaystyle \mathbf {L} =m\mathbf {r} \times \mathbf {v} =mr^{2}\left({\dot {\theta }}\,{\hat {\boldsymbol {\varphi }}}-{\dot {\varphi }}\sin \theta \,\mathbf {\hat {\boldsymbol {\theta }}} \right).}$

Momento angular en cualquier número de dimensiones.

El momento angular se puede definir en términos del producto vectorial sólo en tres dimensiones. Definirlo como bivector , donde es el producto exterior , es válido en cualquier número de dimensiones. Este producto exterior es equivalente a un tensor antisimétrico de grado 2, que también se aplica en cualquier número de dimensiones. Es decir, si es un vector de posición y es el vector de momento lineal, entonces podemos definir ${\displaystyle \mathbf {L} =\mathbf {r} \wedge \mathbf {p} }$ ${\displaystyle \wedge }$ ${\displaystyle x_{i}}$ ${\displaystyle p_{i}}$

$${\displaystyle M_{ij}=x_{i}p_{j}-p_{i}x_{j}}$$

En el caso general de momentos angulares sumados de múltiples partículas, este tensor antisimétrico tiene componentes independientes (grados de libertad), donde es el número de dimensiones. ^[a] En el caso tridimensional habitual tiene 3 componentes independientes, lo que nos permite identificarlo con un pseudovector tridimensional . Los componentes de este vector se relacionan con los componentes del tensor de rango 2 de la siguiente manera: ${\displaystyle n(n-1)/2}$ ${\displaystyle n}$ ${\displaystyle \mathbf {M} =(M_{x},M_{y},M_{z})}$

$${\displaystyle M_{ij}={\begin{pmatrix}0&M_{z}&-M_{y}\\-M_{z}&0&M_{x}\\M_{y}&-M_{x}&0\end{pmatrix}}}$$

Analogía con el momento lineal

El momento angular puede describirse como el análogo rotacional del momento lineal . Al igual que el momento lineal, involucra elementos de masa y desplazamiento . A diferencia del momento lineal, también involucra elementos de posición y forma .

Muchos problemas de física involucran materia en movimiento alrededor de cierto punto en el espacio, ya sea en rotación real alrededor de él, o simplemente moviéndose más allá de él, donde se desea saber qué efecto tiene la materia en movimiento sobre ese punto: ¿puede ejercer energía sobre él? o realizar un trabajo al respecto? La energía , la capacidad de realizar trabajo , se puede almacenar en la materia poniéndola en movimiento, una combinación de su inercia y su desplazamiento. La inercia se mide por su masa y el desplazamiento por su velocidad . Su producto,

$${\displaystyle {\begin{aligned}({\text{amount of inertia}})\times ({\text{amount of displacement}})&={\text{amount of (inertia⋅displacement)}}\\{\text{mass}}\times {\text{velocity}}&={\text{momentum}}\\m\times v&=p\\\end{aligned}}}$$

es el impulso del asunto . ^[10] Remitir este impulso a un punto central introduce una complicación: el impulso no se aplica al punto directamente. Por ejemplo, una partícula de materia en el borde exterior de una rueda está, en efecto, en el extremo de una palanca de la misma longitud que el radio de la rueda, y su impulso hace girar la palanca alrededor del punto central. Esta palanca imaginaria se conoce como brazo de momento . Tiene el efecto de multiplicar el esfuerzo del impulso en proporción a su longitud, efecto conocido como momento . Por tanto, el momento de la partícula se refiere a un punto particular,

$${\displaystyle {\begin{aligned}({\text{moment arm}})\times ({\text{amount of inertia}})\times ({\text{amount of displacement}})&={\text{moment of (inertia⋅displacement)}}\\{\text{length}}\times {\text{mass}}\times {\text{velocity}}&={\text{moment of momentum}}\\r\times m\times v&=L\\\end{aligned}}}$$

es el momento angular , a veces llamado, como aquí, momento de impulso de la partícula versus ese punto central en particular. La ecuación combina un momento (un brazo de momento giratorio de masa ) con una velocidad lineal (equivalente en línea recta) . La velocidad lineal referida al punto central es simplemente el producto de la distancia y la velocidad angular versus el punto: otro momento. Por lo tanto, el momento angular contiene un momento doble: Simplificando ligeramente, la cantidad es el momento de inercia de la partícula , a veces llamado segundo momento de masa. Es una medida de inercia rotacional. ^[11] ${\displaystyle L=rmv}$ ${\displaystyle m}$ ${\displaystyle r}$ ${\displaystyle v}$ ${\displaystyle r}$ ${\displaystyle \omega }$ ${\displaystyle v=r\omega ,}$ ${\displaystyle L=rmr\omega .}$ ${\displaystyle L=r^{2}m\omega ,}$ ${\displaystyle r^{2}m}$

El momento de inercia (que se muestra aquí), y por lo tanto el momento angular, es diferente para cada configuración de masa y eje de rotación que se muestra .

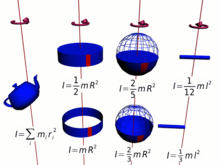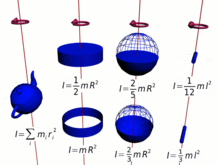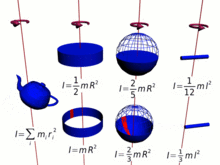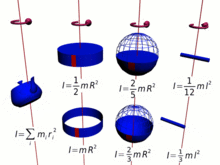
La analogía anterior del momento de traslación y el momento de rotación se puede expresar en forma vectorial: ^{[ cita necesaria ]}

• ${\textstyle \mathbf {p} =m\mathbf {v} }$para movimiento lineal
• ${\displaystyle \mathbf {L} =I{\boldsymbol {\omega }}}$para rotación

La dirección del impulso está relacionada con la dirección de la velocidad en el movimiento lineal. La dirección del momento angular está relacionada con la velocidad angular de rotación.

Debido a que el momento de inercia es una parte crucial del momento angular de giro, este último incluye necesariamente todas las complicaciones del primero, que se calcula multiplicando bits elementales de la masa por los cuadrados de sus distancias al centro de rotación. ^[12] Por lo tanto, el momento total de inercia y el momento angular son una función compleja de la configuración de la materia alrededor del centro de rotación y la orientación de la rotación de los distintos bits.

Para un cuerpo rígido , por ejemplo una rueda o un asteroide, la orientación de rotación es simplemente la posición del eje de rotación versus la materia del cuerpo. Puede pasar o no por el centro de masa , o puede quedar completamente fuera del cuerpo. Para el mismo cuerpo, el momento angular puede tomar un valor diferente para cada eje posible alrededor del cual puede tener lugar la rotación. ^[13] Alcanza un mínimo cuando el eje pasa por el centro de masa. ^[14]

Para una colección de objetos que giran alrededor de un centro, por ejemplo todos los cuerpos del Sistema Solar , las orientaciones pueden estar algo organizadas, como lo está el Sistema Solar, con la mayoría de los ejes de los cuerpos cerca del eje del sistema. Sus orientaciones también pueden ser completamente aleatorias.

En resumen, cuanto más masa y más lejos esté del centro de rotación (cuanto más largo sea el brazo de momento ), mayor será el momento de inercia, y por tanto mayor será el momento angular para una velocidad angular determinada . En muchos casos, el momento de inercia y, por tanto, el momento angular, se pueden simplificar mediante, ^[15]

yo = k 2 metro , {\displaystyle I=k^{2}m,}

radio de giro ${\displaystyle k}$ ${\displaystyle m}$

De manera similar, para una masa puntual, el momento de inercia se define como, ${\displaystyle m}$

$${\displaystyle I=r^{2}m}$$

radio ${\displaystyle r}$

y para cualquier colección de partículas como la suma, ${\displaystyle m_{i}}$

$${\displaystyle \sum _{i}I_{i}=\sum _{i}r_{i}^{2}m_{i}}$$

La dependencia del momento angular de la posición y la forma se refleja en sus unidades versus el momento lineal: kg⋅m ² /s o N⋅m⋅s para el momento angular versus kg⋅m/s o N⋅s para el momento lineal. Al calcular el momento angular como el producto del momento de inercia por la velocidad angular, la velocidad angular debe expresarse en radianes por segundo, donde el radian asume el valor adimensional de la unidad. (Al realizar un análisis dimensional, puede resultar productivo utilizar un análisis orientativo que trate los radianes como una unidad base, pero esto no se hace en el sistema internacional de unidades ). Las unidades de momento angular se pueden interpretar como par ⋅tiempo. Un objeto con momento angular de L N⋅m⋅s se puede reducir a velocidad angular cero mediante un impulso angular de L N⋅m⋅s . ^{[16] [17]}

El plano perpendicular al eje del momento angular y que pasa por el centro de masa ^[18] a veces se denomina plano invariable , porque la dirección del eje permanece fija si sólo las interacciones de los cuerpos dentro del sistema, libres de influencias externas, son considerados. ^[19] Uno de esos planos es el plano invariable del Sistema Solar .

Momento angular y par

La segunda ley del movimiento de Newton se puede expresar matemáticamente,

$${\displaystyle \mathbf {F} =m\mathbf {a} ,}$$

fuerzamasaaceleración

$${\displaystyle \mathbf {L} =I{\boldsymbol {\omega }}}$$

derivada

τ = re yo re t ω + yo re ω re t . {\displaystyle {\boldsymbol {\tau }}={\frac {dI}{dt}}{\boldsymbol {\omega }}+I{\frac {d{\boldsymbol {\omega }}}{dt}} .}

Como el momento de inercia es , se deduce que , y que se reduce a ${\displaystyle mr^{2}}$ ${\displaystyle {\frac {dI}{dt}}=2mr{\frac {dr}{dt}}=2rp_{||}}$ ${\displaystyle {\frac {d\mathbf {L} }{dt}}=I{\frac {d{\boldsymbol {\omega }}}{dt}}+2rp_{||}{\boldsymbol {\omega }},}$

$${\displaystyle {\boldsymbol {\tau }}=I{\boldsymbol {\alpha }}+2rp_{||}{\boldsymbol {\omega }}.}$$

Conservación del momento angular

Una patinadora artística en un giro utiliza la conservación del momento angular: disminuir su momento de inercia al contraer los brazos y las piernas aumenta su velocidad de rotación .

Consideraciones Generales

Un análogo rotacional de la tercera ley del movimiento de Newton podría escribirse: "En un sistema cerrado , no se puede ejercer ningún torque sobre ninguna materia sin que se ejerza sobre alguna otra materia un torque igual y opuesto alrededor del mismo eje". ^[20] Por lo tanto, el momento angular se puede intercambiar entre objetos en un sistema cerrado, pero el momento angular total antes y después de un intercambio permanece constante (se conserva). ^[21]

Visto de otra manera, un análogo rotacional de la primera ley del movimiento de Newton podría escribirse: "Un cuerpo rígido continúa en un estado de rotación uniforme a menos que actúe por una influencia externa". ^[20] Por lo tanto , sin ninguna influencia externa que actúe sobre él, el momento angular original del sistema permanece constante . ^[22]

La conservación del momento angular se utiliza para analizar el movimiento de la fuerza central . Si la fuerza neta sobre un cuerpo se dirige siempre hacia algún punto, el centro , entonces no hay torsión sobre el cuerpo con respecto al centro, ya que toda la fuerza se dirige a lo largo del vector radio y ninguna es perpendicular al radio. . Matemáticamente, el torque porque en este caso y son vectores paralelos. Por tanto, el momento angular del cuerpo con respecto al centro es constante. Este es el caso de la atracción gravitacional en las órbitas de planetas y satélites , donde la fuerza gravitacional siempre se dirige hacia el cuerpo primario y los cuerpos en órbita conservan el momento angular intercambiando distancia y velocidad a medida que se mueven alrededor del primario. El movimiento de fuerza central también se utiliza en el análisis del modelo atómico de Bohr . ${\displaystyle {\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} =\mathbf {0} ,}$ ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {F} }$

Para un planeta, el momento angular se distribuye entre el giro del planeta y su revolución en su órbita, y estos a menudo se intercambian mediante varios mecanismos. La conservación del momento angular en el sistema Tierra-Luna da como resultado la transferencia del momento angular de la Tierra a la Luna, debido al par de marea que la Luna ejerce sobre la Tierra. Esto, a su vez, da como resultado una desaceleración de la velocidad de rotación de la Tierra, de aproximadamente 65,7 nanosegundos por día, ^[23] y un aumento gradual del radio de la órbita de la Luna, de aproximadamente 3,82 centímetros por año. ^[24]

El par causado por las dos fuerzas opuestas F _g y − F _g provoca un cambio en el momento angular L en la dirección de ese par (ya que el par es la derivada del momento angular con el tiempo). Esto hace que la parte superior precese .

La conservación del momento angular explica la aceleración angular de un patinador sobre hielo cuando acerca sus brazos y piernas al eje vertical de rotación. Al acercar parte de la masa de su cuerpo al eje, disminuyen el momento de inercia de su cuerpo. Debido a que el momento angular es el producto del momento de inercia y la velocidad angular , si el momento angular permanece constante (se conserva), entonces la velocidad angular (velocidad de rotación) del patinador debe aumentar.

El mismo fenómeno produce un giro extremadamente rápido de estrellas compactas (como enanas blancas , estrellas de neutrones y agujeros negros ) cuando se forman a partir de estrellas mucho más grandes y con rotación más lenta.

La conservación no siempre es una explicación completa de la dinámica de un sistema, pero es una limitación clave. Por ejemplo, una peonza está sujeta a un par gravitacional que la hace inclinarse y cambiar el momento angular alrededor del eje de nutación , pero si se ignora la fricción en el punto de contacto giratorio, tiene un momento angular conservado alrededor de su eje de giro y otro alrededor de su eje de rotación. eje de precesión . Además, en cualquier sistema planetario , los planetas, las estrellas, los cometas y los asteroides pueden moverse de numerosas y complicadas formas, pero sólo de manera que se conserve el momento angular del sistema.

El teorema de Noether establece que cada ley de conservación está asociada con una simetría (invariante) de la física subyacente. La simetría asociada con la conservación del momento angular es la invariancia rotacional . El hecho de que la física de un sistema no cambie si se gira en cualquier ángulo alrededor de un eje implica que el momento angular se conserva. ^[25] Por esta razón, según la Relatividad General, la conservación del momento angular sólo es aproximada en un espacio-tiempo curvo, que generalmente no tiene tales simetrías; y su propia definición puede fallar a escalas cósmicas (ver Momento angular § Momento angular en la relatividad general).

Relación con la segunda ley del movimiento de Newton

Si bien la conservación total del momento angular puede entenderse separadamente de las leyes del movimiento de Newton como derivadas del teorema de Noether en sistemas simétricos sometidos a rotaciones, también puede entenderse simplemente como un método eficiente de cálculo de resultados a los que también se puede llegar directamente a partir de la segunda ley de Newton. ley, junto con las leyes que gobiernan las fuerzas de la naturaleza (como la tercera ley de Newton, las ecuaciones de Maxwell y la fuerza de Lorentz ). De hecho, dadas las condiciones iniciales de posición y velocidad para cada punto, y las fuerzas en tal condición, se puede utilizar la segunda ley de Newton para calcular la segunda derivada de la posición, y resolver esto proporciona información completa sobre el desarrollo del sistema físico con tiempo. ^[26] Tenga en cuenta, sin embargo, que esto ya no es cierto en la mecánica cuántica , debido a la existencia del espín de las partículas , que es un momento angular que no puede describirse mediante el efecto acumulativo de movimientos puntuales en el espacio.

Como ejemplo, considere la disminución del momento de inercia , por ejemplo, cuando un patinador artístico tira de sus manos, acelerando el movimiento circular. En términos de conservación del momento angular, tenemos, para el momento angular L , momento de inercia I y velocidad angular ω :

$${\displaystyle 0=dL=d(I\cdot \omega )=dI\cdot \omega +I\cdot d\omega }$$

Usando esto, vemos que el cambio requiere una energía de:

$${\displaystyle dE=d\left({\tfrac {1}{2}}I\cdot \omega ^{2}\right)={\tfrac {1}{2}}dI\cdot \omega ^{2}+I\cdot \omega \cdot d\omega =-{\tfrac {1}{2}}dI\cdot \omega ^{2}}$$

Esto se puede comparar con el trabajo realizado calculado utilizando las leyes de Newton. Cada punto del cuerpo giratorio se acelera, en cada punto del tiempo, con una aceleración radial de:

$${\displaystyle -r\cdot \omega ^{2}}$$

Observemos un punto de masa m , cuyo vector de posición con respecto al centro de movimiento es perpendicular al eje z en un momento dado y se encuentra a una distancia z . La fuerza centrípeta sobre este punto, manteniendo el movimiento circular, es:

$${\displaystyle -m\cdot z\cdot \omega ^{2}}$$

Por tanto, el trabajo necesario para mover este punto a una distancia dz más alejada del centro de movimiento es:

$${\displaystyle dW=-m\cdot z\cdot \omega ^{2}\cdot dz=-m\cdot \omega ^{2}\cdot d\left({\tfrac {1}{2}}z^{2}\right)}$$

Para un cuerpo no puntual, se debe integrar sobre esto, reemplazando m por la densidad de masa por unidad z . Esto da:

$${\displaystyle dW=-{\tfrac {1}{2}}dI\cdot \omega ^{2}}$$

que es exactamente la energía necesaria para mantener conservado el momento angular.

Tenga en cuenta que el cálculo anterior también se puede realizar por masa, utilizando únicamente cinemática . Así, el fenómeno del patinador artístico que acelera la velocidad tangencial mientras tira de sus manos hacia adentro puede entenderse de la siguiente manera en un lenguaje sencillo: las palmas de las patinadoras no se mueven en línea recta, por lo que aceleran constantemente hacia adentro, pero no ganan velocidad adicional porque la la aceleración siempre se realiza cuando su movimiento hacia adentro es cero. Sin embargo, esto es diferente cuando se acercan las palmas de las manos al cuerpo: la aceleración debida a la rotación ahora aumenta la velocidad; pero debido a la rotación, el aumento de velocidad no se traduce en una velocidad significativa hacia el interior, sino en un aumento de la velocidad de rotación.

Principio de acción estacionaria

En mecánica clásica se puede demostrar que la invariancia rotacional de la acción funcional implica la conservación del momento angular. La acción se define en la física clásica como una función de posiciones, a menudo representada por el uso de corchetes, y los tiempos final e inicial. Asume la siguiente forma en coordenadas cartesianas: ${\displaystyle x_{i}(t)}$

$${\displaystyle S\left([x_{i}];t_{1},t_{2}\right)\equiv \int _{t_{1}}^{t_{2}}dt\left({\frac {1}{2}}m{\frac {dx_{i}}{dt}}\ {\frac {dx_{i}}{dt}}-V(x_{i})\right)}$$

${\textstyle \delta S=S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right)-S\left([x_{i}];t_{1},t_{2}\right)=0}$

Bajo la transformación, la acción se convierte en: ${\displaystyle x_{i}\rightarrow x_{i}+\delta x_{i}}$

$${\displaystyle S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right)=\!\int _{t_{1}}^{t_{2}}dt\left({\frac {1}{2}}m{\frac {d(x_{i}+\delta x_{i})}{dt}}{\frac {d(x_{i}+\delta x_{i})}{dt}}-V(x_{i}+\delta x_{i})\right)}$$

donde podemos emplear la expansión de los términos hasta primer orden en : ${\textstyle \delta x_{i}}$

$${\displaystyle {\begin{aligned}{\frac {d(x_{i}+\delta x_{i})}{dt}}{\frac {(dx_{i}+\delta x_{i})}{dt}}&\simeq {\frac {dx_{i}}{dt}}{\frac {dx_{i}}{dt}}-2{\frac {d^{2}x_{i}}{dt^{2}}}\delta x_{i}+2{\frac {d}{dt}}\left(\delta x_{i}{\frac {dx_{i}}{dt}}\right)\\V(x_{i}+\delta x_{i})&\simeq V(x_{i})+\delta x_{i}{\frac {\partial V}{\partial x_{i}}}\\\end{aligned}}}$$

$${\displaystyle S[x_{i}+\delta x_{i}]\simeq S[x_{i}]+\int _{t_{1}}^{t_{2}}dt\,\delta x_{i}\left(-{\frac {\partial V}{\partial x_{i}}}-m{\frac {d^{2}x_{i}}{dt^{2}}}\right)+m\int _{t_{1}}^{t_{2}}dt{\frac {d}{dt}}\left(\delta x_{i}{\frac {dx_{i}}{dt}}\right).}$$

Dado que todas las rotaciones se pueden expresar como matriz exponencial de matrices simétricas sesgadas, es decir. como donde es una matriz simétrica sesgada y es un ángulo de rotación, podemos expresar el cambio de coordenadas debido a la rotación , hasta el primer orden de ángulo de rotación infinitesimal, como: ${\displaystyle R({\hat {n}},\theta )=e^{M\theta }}$ ${\displaystyle M}$ ${\displaystyle \theta }$ ${\displaystyle R({\hat {n}},\delta \theta )}$ ${\displaystyle \delta \theta }$

$${\displaystyle \delta x_{i}=M_{ij}x_{j}\delta \theta .}$$

Combinando la ecuación de movimiento y la invariancia rotacional de acción , obtenemos de las ecuaciones anteriores que:

$${\displaystyle 0=\delta S=\int _{t_{1}}^{t_{2}}dt{\frac {d}{dt}}\left(m{\frac {dx_{i}}{dt}}\delta x_{i}\right)=M_{ij}\,\delta \theta \,m\,x_{j}{\frac {dx_{i}}{dt}}{\Bigg \vert }_{t_{1}}^{t_{2}}}$$

${\displaystyle M_{ij}}$ ${\displaystyle M_{ij}=-M_{ji},}$

$${\displaystyle \ell _{ij}(t):=m\left(x_{i}{\frac {dx_{j}}{dt}}-x_{j}{\frac {dx_{i}}{dt}}\right),}$$

como . Esto corresponde a la conservación del momento angular durante todo el movimiento. ^[27] ${\displaystyle \ell _{ij}(t_{1})=\ell _{ij}(t_{2})}$

Formalismo lagrangiano

En la mecánica lagrangiana , el momento angular de rotación alrededor de un eje dado es el momento conjugado de la coordenada generalizada del ángulo alrededor del mismo eje. Por ejemplo, el momento angular alrededor del eje z es: ${\displaystyle L_{z}}$

$${\displaystyle L_{z}={\frac {\partial {\cal {L}}}{\partial {\dot {\theta }}_{z}}}}$$

${\displaystyle {\cal {L}}}$ ${\displaystyle \theta _{z}}$

Tenga en cuenta que , la derivada del ángulo en el tiempo, es la velocidad angular . Normalmente, el lagrangiano depende de la velocidad angular a través de la energía cinética: esta última se puede escribir separando la velocidad en su parte radial y tangencial, siendo la parte tangencial en el plano xy, alrededor del eje z, igual a: ${\displaystyle {\dot {\theta }}_{z}}$ ${\displaystyle \omega _{z}}$

$${\displaystyle \sum _{i}{\tfrac {1}{2}}m_{i}{v_{T}}_{i}^{2}=\sum _{i}{\tfrac {1}{2}}m_{i}\left(x_{i}^{2}+y_{i}^{2}\right){{\omega _{z}}_{i}}^{2}}$$

mv _Tω _z

Para un cuerpo que no es puntual, con densidad ρ , tenemos en cambio:

$${\displaystyle {\frac {1}{2}}\int \rho (x,y,z)\left(x_{i}^{2}+y_{i}^{2}\right){{\omega _{z}}_{i}}^{2}\,dx\,dy={\frac {1}{2}}{I_{z}}_{i}{{\omega _{z}}_{i}}^{2}}$$

^[28]I _z

Por lo tanto, suponiendo que la energía potencial no depende de ω _z (esta suposición puede fallar para sistemas electromagnéticos), tenemos el momento angular del i -ésimo objeto:

$${\displaystyle {\begin{aligned}{L_{z}}_{i}&={\frac {\partial {\cal {L}}}{\partial {{\omega _{z}}_{i}}}}={\frac {\partial E_{k}}{\partial {{\omega _{z}}_{i}}}}\\&={I_{z}}_{i}\cdot {\omega _{z}}_{i}\end{aligned}}}$$

Hasta ahora hemos rotado cada objeto en un ángulo distinto; También podemos definir un ángulo general θ _z mediante el cual rotamos todo el sistema, rotando así también cada objeto alrededor del eje z, y tenemos el momento angular general:

$${\displaystyle L_{z}=\sum _{i}{I_{z}}_{i}\cdot {\omega _{z}}_{i}}$$

De las ecuaciones de Euler-Lagrange se deduce que:

$${\displaystyle 0={\frac {\partial {\cal {L}}}{\partial {{\theta _{z}}_{i}}}}-{\frac {d}{dt}}\left({\frac {\partial {\cal {L}}}{\partial {{{\dot {\theta }}_{z}}_{i}}}}\right)={\frac {\partial {\cal {L}}}{\partial {{\theta _{z}}_{i}}}}-{\frac {d{L_{z}}_{i}}{dt}}}$$

Como el lagrangiano depende de los ángulos del objeto sólo a través del potencial, tenemos:

$${\displaystyle {\frac {d{L_{z}}_{i}}{dt}}={\frac {\partial {\cal {L}}}{\partial {{\theta _{z}}_{i}}}}=-{\frac {\partial V}{\partial {{\theta _{z}}_{i}}}}}$$

iésimo

Supongamos que el sistema es invariante a las rotaciones, de modo que el potencial es independiente de una rotación general según el ángulo θ _z (por lo tanto, puede depender de los ángulos de los objetos sólo a través de sus diferencias, en la forma ). Por lo tanto obtenemos para el momento angular total: ${\displaystyle V({\theta _{z}}_{i},{\theta _{z}}_{j})=V({\theta _{z}}_{i}-{\theta _{z}}_{j})}$

$${\displaystyle {\frac {dL_{z}}{dt}}=-{\frac {\partial V}{\partial {\theta _{z}}}}=0}$$

Este análisis se puede repetir por separado para cada eje, dando una conversación del vector del momento angular. Sin embargo, los ángulos alrededor de los tres ejes no pueden tratarse simultáneamente como coordenadas generalizadas, ya que no son independientes; en particular, dos ángulos por punto son suficientes para determinar su posición. Si bien es cierto que en el caso de un cuerpo rígido, describirlo completamente requiere, además de tres grados de libertad traslacionales , también la especificación de tres grados de libertad rotacionales; sin embargo, estos no pueden definirse como rotaciones alrededor de los ejes cartesianos (ver Ángulos de Euler ). Esta advertencia se refleja en la mecánica cuántica en las relaciones de conmutación no triviales de los diferentes componentes del operador de momento angular .

Formalismo hamiltoniano

De manera equivalente, en la mecánica hamiltoniana, el hamiltoniano puede describirse como una función del momento angular. Como antes, la parte de la energía cinética relacionada con la rotación alrededor del eje z para el i -ésimo objeto es:

$${\displaystyle {\frac {1}{2}}{I_{z}}_{i}{{\omega _{z}}_{i}}^{2}={\frac {{{L_{z}}_{i}}^{2}}{2{I_{z}}_{i}}}}$$

que es análogo a la dependencia de la energía sobre el momento a lo largo del eje z, . ${\displaystyle {\frac {{{p_{z}}_{i}}^{2}}{{2m}_{i}}}}$

Las ecuaciones de Hamilton relacionan el ángulo alrededor del eje z con su momento conjugado, el momento angular alrededor del mismo eje:

$${\displaystyle {\begin{aligned}{\frac {d{\theta _{z}}_{i}}{dt}}&={\frac {\partial {\cal {H}}}{\partial {L_{z}}_{i}}}={\frac {{L_{z}}_{i}}{{I_{z}}_{i}}}\\{\frac {d{L_{z}}_{i}}{dt}}&=-{\frac {\partial {\cal {H}}}{\partial {\theta _{z}}_{i}}}=-{\frac {\partial V}{\partial {\theta _{z}}_{i}}}\end{aligned}}}$$

La primera ecuación da

$${\displaystyle {L_{z}}_{i}={I_{z}}_{i}\cdot {{{\dot {\theta }}_{z}}_{i}}={I_{z}}_{i}\cdot {\omega _{z}}_{i}}$$

Y así obtenemos los mismos resultados que en el formalismo lagrangiano.

Tenga en cuenta que para combinar todos los ejes, escribimos la energía cinética como:

$${\displaystyle E_{k}={\frac {1}{2}}\sum _{i}{\frac {|{\bf {{p}_{i}|^{2}}}}{2m_{i}}}=\sum _{i}\left({\frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{\frac {1}{2}}{\bf {{L}_{i}}}^{\textsf {T}}{I_{i}}^{-1}{\bf {{L}_{i}}}\right)}$$

donde p _r es el impulso en la dirección radial y el momento de inercia es una matriz tridimensional ; las letras en negrita representan vectores tridimensionales.

Para cuerpos puntuales tenemos:

$${\displaystyle E_{k}=\sum _{i}\left({\frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{\frac {|{\bf {{L}_{i}}}|^{2}}{2m_{i}{r_{i}}^{2}}}\right)}$$

Esta forma de la parte de energía cinética del hamiltoniano es útil para analizar problemas de potencial central y se transforma fácilmente en un marco de trabajo de mecánica cuántica (por ejemplo, en el problema del átomo de hidrógeno ).

Ejemplo

La pelota en una cuerda

Introducción

El ejemplo de Ball on a String es un sistema ideal destinado a mostrar las consecuencias de la Segunda Ley de Euler:

(1) ${\displaystyle {dL \over dt}=T}$

¿Dónde está el momento angular, el tiempo y el par externo total que actúa sobre el objeto giratorio (rígido)? ${\displaystyle L}$ ${\displaystyle t}$ ${\displaystyle T}$

Supuestos: una bola de masa está unida a una cuerda que gira a una velocidad inicial angular alrededor de un eje vertical en un plano horizontal sin fricción , introducida para equilibrar el peso de la bola, mientras que una fuerza vertical tira de la cuerda hacia abajo, acortando la cuerda y causando la misma bola. para cerrar su distancia desde el eje de rotación (desde hacia cualquier tipo, por ejemplo, en un intervalo de tiempo determinado ): ${\displaystyle m}$ ${\displaystyle \omega _{0}}$ ${\displaystyle {\vec {z}}}$ ${\displaystyle \alpha }$ ${\displaystyle F}$ ${\displaystyle r_{0}}$ ${\displaystyle r}$ ${\displaystyle r<r_{0}}$ ${\displaystyle t-t_{0}}$

Figura 1 : Imagen de bola estándar en una cuerda

A lo largo del plano de apoyo de la bola, simplificando aún más los supuestos:

1. Cuerda infinitamente rígida, sin masa y poco flexible.
2. Sin resistencia al aire.
3. Sin fricción a lo largo del eje de la cuerda.
4. Fuerza de tracción paralela (coincidente) al eje de rotación. ${\displaystyle F}$

Conservación del momento angular (CoAM), en el caso ideal

Bajo tales supuestos, el par externo total ejercido sobre la bola a lo largo del eje es cero y (1) se puede reescribir como: ${\displaystyle T}$ ${\displaystyle {\vec {z}}}$

(2) ${\displaystyle {dL \over dt}=0}$

Que define CoAM como y por lo tanto , que es equivalencia en dos distancias distintas y . ${\displaystyle dL=0}$ ${\displaystyle L(r_{0})=L(r)}$ ${\displaystyle L}$ ${\displaystyle r_{0}}$ ${\displaystyle r}$

Siendo la pelota Momento de Inercia (MoI) con respecto al eje de rotación a una distancia y el mismo MoI después de la retracción de la cuerda, siendo el momento angular , (2) se convierte en: ${\displaystyle J_{0}=mr_{0}^{2}}$ ${\displaystyle r_{0}}$ ${\displaystyle J=mr^{2}}$ ${\displaystyle L=J\omega }$

(3) , indicando que no cambia en el intervalo de tiempo ${\displaystyle dL=d(mr^{2}\omega )=0}$ ${\displaystyle L}$ ${\displaystyle t_{0}-t}$ ( ) y por lo tanto , omitiendo pasos: ${\displaystyle r_{0}\to r}$ ${\displaystyle mr^{2}\omega =mr_{0}^{2}\omega _{0}}$

(4) la velocidad angular final de la bola después de la retracción de la cuerda. ${\displaystyle \omega ={\frac {r_{0}^{2}}{r^{2}}}\omega _{0}}$

Es posible llegar a la misma conclusión también expresando (2) como:

(5) (equilibrio entre la fuerza de Coriolis y el par con respecto al eje de rotación y la inercia rotacional) que también es: ${\displaystyle {dL \over dt}={d(mr^{2}\omega ) \over dt}=2mr{\dot {r}}\omega +mr^{2}{\dot {\omega }}=2{\dot {r}}\omega +r{\dot {\omega }}=0}$

(6) que, después de la integración de ambos miembros entre y es exactamente (4). ${\displaystyle {d\omega \over \omega }=-2{dr \over r}}$ ${\displaystyle (\omega _{0},\omega )}$ ${\displaystyle (r_{0},r)}$

Las ecuaciones (2) (6) expresan CoAM nuevamente en el único caso ideal en el que ninguna perturbación altera la dinámica de la pelota y para el sistema específico de Bola sobre una Cuerda se traduce en la introducción del plano de soporte y simplificaciones adicionales (1.,2. ,3.,4.) conduciendo al Caso Ideal de ausencia de pares externos ( ${\displaystyle \to }$ ${\displaystyle T=0}$ ) .

Conservación del momento angular (CoAM) frente a conservación de la energía rotacional (CoRE) en el caso ideal

Para analizar mejor el sistema de bola sobre una cuerda todavía en el caso ideal, tendremos en cuenta tanto la velocidad angular de la bola alrededor del eje de rotación como su velocidad lineal a lo largo de la línea de la cuerda mientras esta última está retraída. ${\displaystyle \omega }$ ${\displaystyle {\vec {z}}}$ ${\displaystyle v}$

Figura 2 : Componentes lineales de la velocidad de la pelota en el caso ideal.

La energía cinética total de la bola es: ${\displaystyle K}$

(7) (que también podría escribirse simplemente sumando la energía cinética de ambos componentes de la velocidad lineal de la bola, y : que es (7)). ${\displaystyle K={\frac {1}{2}}J\omega ^{2}+{\frac {1}{2}}mv^{2}}$ ${\displaystyle v_{r}=\omega r}$ ${\displaystyle v}$ ${\displaystyle K={\frac {1}{2}}m\omega ^{2}r^{2}+{\frac {1}{2}}mv^{2}}$

En el instante en que la cuerda está estable, por lo tanto , la pelota transporta solo energía de rotación: ${\displaystyle t_{0}}$ ${\displaystyle v=v_{0}=0}$

(8) ${\displaystyle K_{0}={\frac {1}{2}}J_{0}\omega _{0}^{2}}$

En cambio, en el instante genérico, la cuerda se retrae y la energía cinética del sistema de bola en una cuerda ahora se expresa mediante (7). ${\displaystyle t}$ ${\displaystyle v\neq 0}$

El principio de conservación de energía ( CoE ) se puede escribir así como (7) = (8) : ${\displaystyle K=K_{0}}$

(9) significado: ${\displaystyle {\frac {1}{2}}J\omega ^{2}+{\frac {1}{2}}mv^{2}={\frac {1}{2}}J_{0}\omega _{0}^{2}}$

(10) el cambio de velocidad angular durante la retracción de la cuerda. ${\displaystyle \omega ={\sqrt {\frac {r_{0}^{2}\omega _{0}^{2}-v^{2}}{r^{2}}}}}$

La ecuación (10) es diferente de la clásica (4), siendo la velocidad angular proporcional no al cuadrado de la relación de retracción sino a su raíz cuadrada. ${\displaystyle {r_{0}^{2}} \over {r^{2}}}$

Si es la velocidad angular final obtenida mediante (10) modelo CoE y la obtenida mediante (4) modelo CoAM, siempre será: ${\displaystyle \omega _{K}}$ ${\displaystyle \omega _{L}}$

(11) ${\displaystyle \omega _{K}<\omega _{L}}$

Y hay que señalar además que:

(12) << ${\displaystyle \lim _{v\to 0}\omega _{K}={\frac {r_{0}}{r}}\omega _{0}}$ ${\displaystyle {\frac {r_{0}^{2}}{r^{2}}}\omega _{0}=\omega _{L}}$

y:

(13) ${\displaystyle \lim _{v\to 0}({\frac {1}{2}}mv^{2}+{\frac {1}{2}}J\omega ^{2})={\frac {1}{2}}J\omega ^{2}}$

Entonces, para velocidades de retracción lentas, la ecuación (9) se convierte en: ${\displaystyle v\simeq 0}$

(14) que expresa la conservación de la energía rotacional (CoRE), de lo contrario no se conserva para velocidades de retracción no despreciables cuando se aplica (9) CoE. La ecuación (14) significa una velocidad angular de la bola mientras la cuerda se retrae como: ${\displaystyle {\frac {1}{2}}J\omega ^{2}={\frac {1}{2}}J_{0}\omega _{0}^{2}}$

(15) que puede aceptarse en lugar de (4) bajo el supuesto adecuado. ${\displaystyle \omega ={\frac {r_{0}}{r}}\omega _{0}}$ ${\displaystyle v\simeq 0}$

Diferencias entre los modelos CoAM y CoRE/CoE

A continuación, el gráfico compara la velocidad angular prevista a partir del modelo CoRE y CoAM (ecuación (4) y (15)) cuando se retrae la cuerda:

Figura 3 : Velocidad angular final prevista a partir de los modelos CoRE y CoAM después de la retracción de la cuerda

Figura 4 : Predicción de la velocidad angular final del modelo CoAM a CoRE después de la retracción de la cuerda

Seguramente la ecuación CoRE (15) muestra predicciones más cercanas a la realidad que CoAM porque la primera representa toda la cinética del sistema Ball on a String (rotacional y lineal), mientras que la segunda solo rotacional, lo mismo se aplica para elcaso no despreciable, donde usamos ( 10) CoE en lugar de CoRE. ${\displaystyle v}$

Tendencia CoAM, máquina giratoria Atwood (SAM)

Quitar el plano de soporte de la bola pero mantener las suposiciones (1.,2.,3.,4.), de modo que dejar que la misma bola se mueva también en vertical (ángulo de flexión de la cuerda ) se asemeja a un sistema de bola sobre una cuerda más realista que se puede modelar mediante una simple máquina giratoria Atwood (SAM): ${\displaystyle \phi }$

Figura 5 : Máquina giratoria de Atwood (SAM):una polea de peso insignificante P (para reducir la fricción de la cuerda ) gira alrededor deun eje dentro de un tubo interior lubricado e infinitamente rígido (con respecto a la cuerda) de forma adecuada para evitar vueltas: el tubo alberga un peso insignificante y siempre recto cuerda de acero de longitudmucho mayor que el radio P seleccionado para resistir fuerzas centrífugas: una masa de contrapesorestringida para evitar sus rotaciones y conectada a la cuerda por una rótula que permite que la misma cuerda gire mientras se tira dela bola para acortar su distancia del eje de rotación y acortar la cuerda. Se podría colocar un motor eléctrico encima del conjunto para soportarlo. ${\displaystyle {\vec {z}}}$ ${\displaystyle l}$ ${\displaystyle M}$ ${\displaystyle M}$

Lo cual puede evaluarse mediante un enfoque estándar de Lagrange para escribir la ecuación de movimiento (EoM) SAM:

(dieciséis) ${\displaystyle {\begin{cases}(M+m){\ddot {r}}-mr{\dot {\theta }}^{2}sin^{2}\phi -mr{\dot {\phi }}^{2}=mgcos\phi -Mg\\mr^{2}{\ddot {\theta }}sin^{2}\phi +2m{\dot {r}}{\dot {\theta }}rsin^{2}\phi +mr^{2}{\dot {\theta }}{\dot {\phi }}sin2\phi =0\\mr^{2}{\ddot {\phi }}+2mr{\dot {r}}{\dot {\phi }}-mr^{2}{\dot {\theta }}^{2}sin\phi cos\phi =-mgrsin\phi \end{cases}}}$

Donde es igual que arriba la velocidad angular de la pelota alrededor del eje z , siendo la velocidad angular de la pelota en el plano vertical y la misma velocidad de la pelota a lo largo de la cuerda durante la retracción. ${\displaystyle {\dot {\theta }}=\omega }$ ${\displaystyle {\dot {\phi }}}$ ${\displaystyle {\dot {r}}=v}$

La primera ecuación muestra la dinámica de la pelota a lo largo del eje de la cuerda, la segunda el equilibrio rotacional de la pelota alrededor del eje de rotación y la tercera el mismo equilibrio rotacional en el plano vertical. Se puede observar que cuando la segunda ecuación se puede reescribir como exactamente (6) y, por lo tanto, CoAM (4). Pero este último CoAM muestra solo alrededor del eje z , no hay conservación del momento lineal (a lo largo del eje de la cuerda) ni CoAM en el plano vertical donde el peso de la bola no está equilibrado después de eliminar el supuesto del plano de soporte, por lo que en (1). ${\displaystyle {\vec {z}}}$ ${\displaystyle \phi ={\frac {\pi }{2}}}$ ${\displaystyle mr^{2}{\ddot {\theta }}+2m{\dot {r}}{\dot {\theta }}r=0}$ ${\displaystyle r{\dot {\omega }}+2{\dot {r}}\omega =0}$ ${\displaystyle T\neq 0}$

Lo que significa que no se espera que el modelo SAM de la bola en una cuerda muestre CoAM en la fase transitoria, como se puede mostrar mediante el gráfico de integración EoM numérico (16) de AM:

Figura 6 : Tendencia SAM a CoAM, masa normalizada,mediante integración numérica de EoM. ${\displaystyle m}$ ${\displaystyle L}$

Y al introducir la resistencia del aire (solo en el movimiento de giro del eje z ), la fricción y la rigidez de la cuerda, manteniendo esta última inflexible y sin masa, también desaparece la CoAM del eje z (segunda (16) ecuación):

(17) ${\displaystyle {\begin{cases}(M+m){\ddot {r}}-mr{\dot {\theta }}^{2}sin^{2}\phi -mr{\dot {\phi }}^{2}+c{\dot {r}}+K_{E}r=mgcos\phi -Mg\\mr^{2}{\ddot {\theta }}sin^{2}\phi +2m{\dot {r}}{\dot {\theta }}rsin^{2}\phi +mr^{2}{\dot {\theta }}{\dot {\phi }}sin2\phi +{\frac {3}{2}}K{\dot {\theta }}^{2}r^{3}=0\\mr^{2}{\ddot {\phi }}+2mr{\dot {r}}{\dot {\phi }}-mr^{2}{\dot {\theta }}^{2}sin\phi cos\phi =-mgrsin\phi \end{cases}}}$

Donde ( módulo de Young de la cuerda, sección transversal de la cuerda, longitud de la cuerda) y ( densidad del aire, coeficiente de arrastre para una bola aerodinámica para reducir las turbulencias). ${\displaystyle K_{E}={\frac {EA}{l}}}$ ${\displaystyle E}$ ${\displaystyle A}$ ${\displaystyle l}$ ${\displaystyle K={\frac {1}{2}}\rho _{a}C_{d}A}$ ${\displaystyle \rho _{a}}$ ${\displaystyle C_{d}}$

El motor eléctrico

Cabe señalar que las ecuaciones (16) y (17) están escritas sin considerar el par del motor eléctrico que impulsa el SAM: EoM describe la condición en la que (motor apagado) y el contrapeso se suelta, cuando la distancia de la bola desde el eje de rotación podría disminuir (cadena para " acortar ") o aumentar (cadena para " alargar ") dependiendo del equilibrio entre la fuerza centrífuga y el mismo contrapeso. ${\displaystyle T_{E}}$ ${\displaystyle T_{E}=0}$ ${\displaystyle M}$

Detalles de la MOE SAM

La primera ecuación del sistema (16) trata sobre el equilibrio de fuerzas a lo largo de la cuerda: fuerza inercial de dos masas , luego aceleración centrífuga en el plano vertical y = componente de la fuerza centrífuga debido a la rotación de la bola alrededor del eje z proyectado en la dirección de la cuerda. ${\displaystyle (M+m){\ddot {r}}}$ ${\displaystyle mr{\dot {\phi }}^{2}}$ ${\displaystyle mr{\dot {\theta }}^{2}sin^{2}\phi }$ ${\displaystyle mr{\dot {\theta }}^{2}sin\phi cos({\frac {\pi }{2}}-\phi )}$

La segunda ecuación muestra el equilibrio de pares alrededor del eje z , donde:

• ${\displaystyle mr{\ddot {\theta }}sin\phi *rsin\phi }$es el par de inercia debido a la aceleración angular . ${\displaystyle {\ddot {\theta }}}$
• ${\displaystyle C(\theta )=2m{\dot {\theta }}{\dot {r}}sin\phi *rsin\phi }$el par de torsión de la fuerza de Coriolis (componente de velocidad ). ${\displaystyle {\dot {r}}sin\phi }$
• ${\displaystyle mr^{2}{\dot {\theta }}{\dot {\phi }}sin2\phi =2m{\dot {\theta }}r{\dot {\phi }}cos\phi (=C(\theta \phi ))*rsin\phi }$el par de torsión de la fuerza de Coriolis (componente de velocidad ). ${\displaystyle r{\dot {\phi }}cos\phi }$

La tercera ecuación representa el equilibrio del par en el plano vertical:

• ${\displaystyle mr^{2}{\ddot {\phi }}}$es el par de inercia.
• ${\displaystyle C(\phi )=2m{\dot {r}}{\dot {\phi }}*r}$ torque de la fuerza de Coriolis.
• ${\displaystyle mr{\dot {\theta }}^{2}sin\phi *rcos\phi }$par de la fuerza centrífuga.
• ${\displaystyle mgrsin\phi }$peso de la pelota.

Figura 7 : Diagrama de fuerza -1:y. ${\displaystyle \omega _{\theta }={\dot {\theta }}}$ ${\displaystyle \omega _{\phi }={\dot {\phi }}}$

Figura 8 : Diagrama de fuerza -2

Figura 9 : Velocidad angular de la bolaalrededor del eje z mediante integración numérica EoM. ${\displaystyle \omega }$

Figura 10 :Evoluciónmientras aumenta la velocidad angular de la bola, mediante integración numérica EoM. ${\displaystyle \phi }$ ${\displaystyle {\pi } \over {2}}$ ${\displaystyle \omega }$

________________________________________________________________________________________________________________________________

SAM simplificado, que muestra CoAM

Suponiendo que la bola gira en el plano de soporte de modo que su peso esté equilibrado, sin arrastre de aire y un nuevo coeficiente de fricción (16)-(17) EoM se convierta en: ${\displaystyle \phi ={\frac {\pi }{2}}}$ ${\displaystyle c}$

(18) ${\displaystyle {\begin{cases}(M+m){\ddot {r}}-mr{\dot {\theta }}^{2}+c{\dot {r}}=-Mg\\mr{\ddot {\theta }}+2m{\dot {r}}{\dot {\theta }}=0\end{cases}}}$

Y a continuación se muestran algunos gráficos de la dinámica prevista de la condición SAM y CoAM simplificada:

Figura 11 : Evolución de la distancia de la bola desde el eje de rotación después de soltar el contrapeso (integración numérica EoM). ${\displaystyle M}$

Figura 12 : Evolución de la velocidad angular de la bola después desoltar el contrapeso (integración numérica EoM). ${\displaystyle M}$

Figura 13 : SAM simplificado cumple con CoAM perfecto en el caso ideal.

Figura 14 :Equilibrio de fuerza centrífuga y contrapeso () frente a la distancia de la bola desde el eje de rotación (). ${\displaystyle M}$ ${\displaystyle v=0}$ ${\displaystyle \omega _{\theta }=\omega }$

________________________________________________________________________________________________________________________________

Bola de quilla con cuerda (KBS), CoAM asistida

Como se ve, se propone el clásico ejercicio de Pelota sobre Cuerda siendo la cuerda tirada por una vertical mientras la pelota va girando en el plano horizontal. ${\displaystyle F}$

¿Qué pasa si por el contrario asumimos un plano de giro horizontal y uno vertical? ${\displaystyle F}$

Figura 15 : Bola con quilla en una cuerda

Figura 16 : Diagrama de fuerza KBS.

Las EoM de KBS son, siempre bajo (1.,2.,3.) supuestos:

(19) ${\displaystyle {\begin{cases}{\ddot {r}}-r{\dot {\theta }}^{2}=-gsin\theta \\r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}=-gcos\theta \end{cases}}}$

Que se asemejan claramente a EoM (18) con la diferencia del componente de peso que previene CoAM : los pares externos en el eje de rotación son de hecho diferentes de cero ( ), por lo que no se conservarán como consecuencia de (1). Se conservará sólo cuando se configure un motor eléctrico para equilibrar continuamente con su par el par del peso de la bola que conduce al " CoAM asistido ". ${\displaystyle mgrcos\theta }$ ${\displaystyle {\vec {x}}}$ ${\displaystyle T\neq 0}$ ${\displaystyle L}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle T_{E}}$

Momento angular en mecánica orbital

Si bien en la mecánica clásica el lenguaje del momento angular puede ser reemplazado por las leyes del movimiento de Newton, es particularmente útil para el movimiento en potencial central , como el movimiento planetario en el sistema solar. Así, la órbita de un planeta en el sistema solar se define por su energía, momento angular y ángulos del eje mayor de la órbita con respecto a un sistema de coordenadas.

En astrodinámica y mecánica celeste , una cantidad estrechamente relacionada con el momento angular se define como ^[29]

$${\displaystyle \mathbf {h} =\mathbf {r} \times \mathbf {v} ,}$$

momento angular específicola masala gravedad ${\displaystyle \mathbf {L} =m\mathbf {h} .}$

Cuerpos sólidos

El momento angular también es un concepto extremadamente útil para describir cuerpos rígidos en rotación, como un giroscopio o un planeta rocoso. Para una distribución de masa continua con función de densidad ρ ( r ), un elemento de volumen diferencial dV con vector de posición r dentro de la masa tiene un elemento de masa dm = ρ ( r ) dV . Por tanto, el momento angular infinitesimal de este elemento es:

$${\displaystyle d\mathbf {L} =\mathbf {r} \times dm\mathbf {v} =\mathbf {r} \times \rho (\mathbf {r} )dV\mathbf {v} =dV\mathbf {r} \times \rho (\mathbf {r} )\mathbf {v} }$$

e integrando este diferencial sobre el volumen de toda la masa se obtiene su momento angular total:

$${\displaystyle \mathbf {L} =\int _{V}dV\mathbf {r} \times \rho (\mathbf {r} )\mathbf {v} }$$

En la derivación siguiente, integrales similares a ésta pueden reemplazar las sumas para el caso de masa continua.

Colección de partículas

El momento angular de las partículas i es la suma de los productos cruzados R × M V + Σ r _i × m _i v _i .

Para un conjunto de partículas en movimiento alrededor de un origen arbitrario, es informativo desarrollar la ecuación del momento angular resolviendo su movimiento en componentes alrededor de su propio centro de masa y alrededor del origen. Dado,

• ${\displaystyle m_{i}}$es la masa de la partícula , ${\displaystyle i}$
• ${\displaystyle \mathbf {R} _{i}}$es el vector de posición de la partícula frente al origen, ${\displaystyle i}$
• ${\displaystyle \mathbf {V} _{i}}$es la velocidad de la partícula respecto del origen, ${\displaystyle i}$
• ${\displaystyle \mathbf {R} }$es el vector de posición del centro de masa con respecto al origen,
• ${\displaystyle \mathbf {V} }$es la velocidad del centro de masa con respecto al origen,
• ${\displaystyle \mathbf {r} _{i}}$es el vector de posición de la partícula con respecto al centro de masa, ${\displaystyle i}$
• ${\displaystyle \mathbf {v} _{i}}$es la velocidad de la partícula respecto del centro de masa, ${\displaystyle i}$

La masa total de las partículas es simplemente su suma,

$${\displaystyle M=\sum _{i}m_{i}.}$$

El vector de posición del centro de masa está definido por, ^[30]

$${\displaystyle M\mathbf {R} =\sum _{i}m_{i}\mathbf {R} _{i}.}$$

Mediante inspección,

${\displaystyle \mathbf {R} _{i}=\mathbf {R} +\mathbf {r} _{i}}$y ${\displaystyle \mathbf {V} _{i}=\mathbf {V} +\mathbf {v} _{i}.}$

El momento angular total del conjunto de partículas es la suma del momento angular de cada partícula,

${\displaystyle \mathbf {L} =\sum _{i}\left(\mathbf {R} _{i}\times m_{i}\mathbf {V} _{i}\right)}$     ( 1 )

En expansión , ${\displaystyle \mathbf {R} _{i}}$

${\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\left(\mathbf {R} +\mathbf {r} _{i}\right)\times m_{i}\mathbf {V} _{i}\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} _{i}\right]\end{aligned}}}$

En expansión , ${\displaystyle \mathbf {V} _{i}}$

${\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\mathbf {R} \times m_{i}\left(\mathbf {V} +\mathbf {v} _{i}\right)+\mathbf {r} _{i}\times m_{i}(\mathbf {V} +\mathbf {v} _{i})\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} +\mathbf {R} \times m_{i}\mathbf {v} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} +\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\right]\\&=\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {R} \times m_{i}\mathbf {v} _{i}+\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\end{aligned}}}$

Se puede demostrar que (ver recuadro),

${\displaystyle \sum _{i}m_{i}\mathbf {r} _{i}=\mathbf {0} }$y ${\displaystyle \sum _{i}m_{i}\mathbf {v} _{i}=\mathbf {0} ,}$

por lo tanto, los términos segundo y tercero desaparecen,

${\displaystyle \mathbf {L} =\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}.}$

El primer término se puede reordenar,

${\displaystyle \sum _{i}\mathbf {R} \times m_{i}\mathbf {V} =\mathbf {R} \times \sum _{i}m_{i}\mathbf {V} =\mathbf {R} \times M\mathbf {V} ,}$

y el momento angular total para la colección de partículas es finalmente, ^[31]

${\displaystyle \mathbf {L} =\mathbf {R} \times M\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}}$     ( 2 )

El primer término es el momento angular del centro de masa con respecto al origen. Similar a § Partícula única , a continuación, es el momento angular de una partícula de masa M en el centro de masa que se mueve con velocidad V. El segundo término es el momento angular de las partículas que se mueven con respecto al centro de masa, similar a § Centro de masa fijo , a continuación. El resultado es general: el movimiento de las partículas no se limita a la rotación o revolución alrededor del origen o centro de masa. Las partículas no tienen por qué ser masas individuales, sino que pueden ser elementos de una distribución continua, como por ejemplo un cuerpo sólido.

Reorganizando la ecuación ( 2 ) por identidades vectoriales, multiplicando ambos términos por "uno" y agrupando apropiadamente,

$${\displaystyle {\begin{aligned}\mathbf {L} &=M(\mathbf {R} \times \mathbf {V} )+\sum _{i}\left[m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&={\frac {R^{2}}{R^{2}}}M\left(\mathbf {R} \times \mathbf {V} \right)+\sum _{i}\left[{\frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&=R^{2}M\left({\frac {\mathbf {R} \times \mathbf {V} }{R^{2}}}\right)+\sum _{i}\left[r_{i}^{2}m_{i}\left({\frac {\mathbf {r} _{i}\times \mathbf {v} _{i}}{r_{i}^{2}}}\right)\right],\\\end{aligned}}}$$

da el momento angular total del sistema de partículas en términos de momento de inercia y velocidad angular , ${\displaystyle I}$ ${\displaystyle {\boldsymbol {\omega }}}$

${\displaystyle \mathbf {L} =I_{R}{\boldsymbol {\omega }}_{R}+\sum _{i}I_{i}{\boldsymbol {\omega }}_{i}.}$     ( 3 )

Caso de una sola partícula

En el caso de una sola partícula que se mueve alrededor del origen arbitrario,

$${\displaystyle {\begin{aligned}\mathbf {r} _{i}&=\mathbf {v} _{i}=\mathbf {0} ,\\\mathbf {r} &=\mathbf {R} ,\\\mathbf {v} &=\mathbf {V} ,\\m&=M,\end{aligned}}}$$

$${\displaystyle \sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}=\mathbf {0} ,}$$

$${\displaystyle \sum _{i}I_{i}{\boldsymbol {\omega }}_{i}=\mathbf {0} ,}$$

23

$${\displaystyle \mathbf {L} =\mathbf {R} \times m\mathbf {V} =I_{R}{\boldsymbol {\omega }}_{R}.}$$

Caso de un centro de masa fijo

Para el caso del centro de masa fijo en el espacio con respecto al origen,

$${\displaystyle \mathbf {V} =\mathbf {0} ,}$$

$${\displaystyle \mathbf {R} \times M\mathbf {V} =\mathbf {0} ,}$$

$${\displaystyle I_{R}{\boldsymbol {\omega }}_{R}=\mathbf {0} ,}$$

23

$${\displaystyle \mathbf {L} =\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}=\sum _{i}I_{i}{\boldsymbol {\omega }}_{i}.}$$

Momento angular en relatividad general

El momento de 3 ángulos como bivector (elemento plano) y vector axial , de una partícula de masa m con x instantáneo de 3 posiciones y momento de 3 p .

En la física teórica moderna (siglo XX), el momento angular (sin incluir ningún momento angular intrínseco; ver más abajo) se describe utilizando un formalismo diferente, en lugar de un pseudovector clásico . En este formalismo, el momento angular es la carga de Noether de 2 formas asociada con la invariancia rotacional. Como resultado, el momento angular generalmente no se conserva localmente para los espacios-tiempo curvos generales , a menos que tengan simetría rotacional ^[32] ; mientras que globalmente la noción de conservación del momento angular sólo tiene sentido si el espacio-tiempo es asintóticamente invariante rotacionalmente ^[33] .

En mecánica clásica, el momento angular de una partícula se puede reinterpretar como un elemento plano:

$${\displaystyle \mathbf {L} =\mathbf {r} \wedge \mathbf {p} \,,}$$

producto exteriorproducto cruzadoxp

$${\displaystyle {\begin{aligned}\mathbf {L} &=\left(xp_{y}-yp_{x}\right)\mathbf {e} _{x}\wedge \mathbf {e} _{y}+\left(yp_{z}-zp_{y}\right)\mathbf {e} _{y}\wedge \mathbf {e} _{z}+\left(zp_{x}-xp_{z}\right)\mathbf {e} _{z}\wedge \mathbf {e} _{x}\\&=L_{xy}\mathbf {e} _{x}\wedge \mathbf {e} _{y}+L_{yz}\mathbf {e} _{y}\wedge \mathbf {e} _{z}+L_{zx}\mathbf {e} _{z}\wedge \mathbf {e} _{x}\,,\end{aligned}}}$$

$${\displaystyle L_{ij}=x_{i}p_{j}-x_{j}p_{i}\,.}$$

La velocidad angular también se puede definir como un tensor antisimétrico de segundo orden, con componentes ω _ij . La relación entre los dos tensores antisimétricos viene dada por el momento de inercia que ahora debe ser un tensor de cuarto orden: ^[34]

$${\displaystyle L_{ij}=I_{ijk\ell }\omega _{k\ell }\,.}$$

Nuevamente, esta ecuación en L y ω como tensores es cierta en cualquier número de dimensiones. Esta ecuación también aparece en el formalismo del álgebra geométrica , en el que L y ω son bivectores, y el momento de inercia es una aplicación entre ellos.

En mecánica relativista , el momento angular relativista de una partícula se expresa como un tensor antisimétrico de segundo orden:

$${\displaystyle M_{\alpha \beta }=X_{\alpha }P_{\beta }-X_{\beta }P_{\alpha }}$$

cuatro vectoresX de cuatro posicionesP de cuatroLmomento de masacentro de masa

En cada uno de los casos anteriores, para un sistema de partículas, el momento angular total es simplemente la suma de los momentos angulares de las partículas individuales, y el centro de masa es para el sistema.

Momento angular en mecánica cuántica

En mecánica cuántica , el momento angular (como otras cantidades) se expresa como un operador , y sus proyecciones unidimensionales tienen valores propios cuantificados . El momento angular está sujeto al principio de incertidumbre de Heisenberg , lo que implica que en cualquier momento, sólo una proyección (también llamada "componente") puede medirse con precisión definida; los otros dos siguen siendo inciertos. Por esta razón, el eje de rotación de una partícula cuántica no está definido. Las partículas cuánticas poseen un tipo de momento angular no orbital llamado "giro", pero este momento angular no corresponde a un movimiento de giro. ^[35] En la mecánica cuántica relativista, la definición relativista anterior se convierte en un operador tensorial.

Spin, orbital y momento angular total

Momentos angulares de un objeto clásico .

• Izquierda: el momento angular de "giro" S es en realidad el momento angular orbital del objeto en cada punto.
• Derecha: momento angular orbital extrínseco L alrededor de un eje.
• Arriba: el momento del tensor de inercia I y la velocidad angular ω ( L no siempre es paralela a ω ). ^[36]
• Abajo: impulso p y su posición radial r desde el eje. El momento angular total (giro más orbital) es J. Para una partícula cuántica las interpretaciones son diferentes; El giro de las partículas no tiene la interpretación anterior.

La definición clásica de momento angular puede trasladarse a la mecánica cuántica, reinterpretando r como el operador de posición cuántica y p como el operador de momento cuántico . L es entonces un operador , específicamente llamado operador de momento angular orbital . Las componentes del operador de momento angular satisfacen las relaciones de conmutación del álgebra de Lie so(3). En efecto, estos operadores son precisamente la acción infinitesimal del grupo de rotación sobre el espacio cuántico de Hilbert . ^[37] (Véase también la discusión a continuación sobre los operadores de momento angular como generadores de rotaciones). ${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$

Sin embargo, en física cuántica, existe otro tipo de momento angular, llamado momento angular de espín , representado por el operador de espín S. El espín a menudo se describe como una partícula que literalmente gira alrededor de un eje, pero esta es una imagen engañosa e inexacta: el espín es una propiedad intrínseca de una partícula, no relacionada con ningún tipo de movimiento en el espacio y fundamentalmente diferente del momento angular orbital. Todas las partículas elementales tienen un espín característico (posiblemente cero), ^[38] y casi todas las partículas elementales tienen un espín distinto de cero. ^[39] Por ejemplo , los electrones tienen "espín 1/2" (esto en realidad significa "espín ħ /2"), los fotones tienen "espín 1" (esto en realidad significa "espín ħ") y los mesones pi tienen espín 0. ^{[ 40]}

Finalmente, existe el momento angular total J , que combina el momento angular orbital y de espín de todas las partículas y campos. (Para una partícula, J = L + S. ) La conservación del momento angular se aplica a J , pero no a L o S ; por ejemplo, la interacción espín-órbita permite que el momento angular se transfiera de un lado a otro entre L y S , permaneciendo el total constante. Los electrones y fotones no necesitan tener valores enteros para el momento angular total, pero también pueden tener valores semienteros. ^[41]

En las moléculas , el momento angular total F es la suma del momento angular rovibrónico (orbital) N , el momento angular de espín del electrón S y el momento angular de espín nuclear I. Para los estados singlete electrónicos , el momento angular rovibrónico se denomina J en lugar de N. Como explica Van Vleck, ^[42] los componentes del momento angular rovibrónico molecular referidos a ejes fijos en moléculas tienen relaciones de conmutación diferentes a las de los componentes alrededor de ejes fijos en el espacio.

Cuantización

En mecánica cuántica , el momento angular está cuantificado , es decir, no puede variar continuamente, sino sólo en " saltos cuánticos " entre determinados valores permitidos. Para cualquier sistema, se aplican las siguientes restricciones a los resultados de las mediciones, donde es la constante de Planck reducida y es cualquier vector euclidiano como x, y o z: ${\displaystyle \hbar }$ ${\displaystyle {\hat {n}}}$

En esta onda estacionaria sobre una cuerda circular, el círculo se divide en exactamente 8 longitudes de onda . Una onda estacionaria como esta puede tener 0,1,2 o cualquier número entero de longitudes de onda alrededor del círculo, pero no puede tener un número no entero de longitudes de onda como 8,3. En mecánica cuántica, el momento angular se cuantifica por una razón similar.

La constante de Planck reducida es pequeña para los estándares cotidianos, alrededor de 10 ⁻³⁴ J s , y por lo tanto esta cuantificación no afecta notablemente el momento angular de los objetos macroscópicos. Sin embargo, es muy importante en el mundo microscópico. Por ejemplo, la estructura de las capas y subcapas de electrones en química se ve significativamente afectada por la cuantificación del momento angular. ${\displaystyle \hbar }$

La cuantificación del momento angular fue postulada por primera vez por Niels Bohr en su modelo del átomo y luego predicha por Erwin Schrödinger en su ecuación de Schrödinger .

Incertidumbre

En la definición intervienen seis operadores: los operadores de posición , , y los operadores de impulso , , . Sin embargo, el principio de incertidumbre de Heisenberg nos dice que no es posible conocer simultáneamente estas seis cantidades con precisión arbitraria. Por lo tanto, existen límites a lo que se puede conocer o medir sobre el momento angular de una partícula. Resulta que lo mejor que se puede hacer es medir simultáneamente tanto la magnitud del vector del momento angular como su componente a lo largo de un eje. ${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$ ${\displaystyle r_{x}}$ ${\displaystyle r_{y}}$ ${\displaystyle r_{z}}$ ${\displaystyle p_{x}}$ ${\displaystyle p_{y}}$ ${\displaystyle p_{z}}$

La incertidumbre está estrechamente relacionada con el hecho de que diferentes componentes de un operador de momento angular no conmutan , por ejemplo . (Para conocer las relaciones de conmutación precisas , consulte operador de momento angular ). ${\displaystyle L_{x}L_{y}\neq L_{y}L_{x}}$

Momento angular total como generador de rotaciones.

Como se mencionó anteriormente, el momento angular orbital L se define como en la mecánica clásica: , pero el momento angular total J se define de una manera diferente y más básica: J se define como el "generador de rotaciones". ^[43] Más específicamente, J se define de modo que el operador ${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$

$${\displaystyle R({\hat {n}},\phi )\equiv \exp \left(-{\frac {i}{\hbar }}\phi \,\mathbf {J} \cdot {\hat {\mathbf {n} }}\right)}$$

operador de rotaciónoperador exponencialgrupo de rotación SO(3) ${\displaystyle \phi }$ ${\displaystyle {\hat {\mathbf {n} }}}$

La relación entre el operador de momento angular y los operadores de rotación es la misma que la relación entre las álgebras de Lie y los grupos de Lie en matemáticas. La estrecha relación entre el momento angular y las rotaciones se refleja en el teorema de Noether , que demuestra que el momento angular se conserva siempre que las leyes de la física sean rotacionalmente invariantes.

Momento angular en electrodinámica.

Al describir el movimiento de una partícula cargada en un campo electromagnético , el momento canónico P (derivado del lagrangiano para este sistema) no es invariante de calibre . Como consecuencia, el momento angular canónico L = r × P tampoco es invariante de calibre. En cambio, el impulso físico, el llamado impulso cinético (utilizado a lo largo de este artículo), es (en unidades SI )

$${\displaystyle \mathbf {p} =m\mathbf {v} =\mathbf {P} -e\mathbf {A} }$$

donde e es la carga eléctrica de la partícula y A el potencial vectorial magnético del campo electromagnético. El momento angular invariante de calibre, es decir, el momento angular cinético , viene dado por

$${\displaystyle \mathbf {K} =\mathbf {r} \times (\mathbf {P} -e\mathbf {A} )}$$

La interacción con la mecánica cuántica se analiza con más detalle en el artículo sobre relaciones de conmutación canónicas .

Momento angular en óptica.

En la electrodinámica clásica de Maxwell, el vector de Poynting es una densidad de momento lineal del campo electromagnético. ^[44]

$${\displaystyle \mathbf {S} (\mathbf {r} ,t)=\epsilon _{0}c^{2}\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t).}$$

El vector de densidad de momento angular viene dado por un producto vectorial como en la mecánica clásica: ^[45] ${\displaystyle \mathbf {L} (\mathbf {r} ,t)}$

$${\displaystyle \mathbf {l} (\mathbf {r} ,t)=\epsilon _{0}\mu _{0}\mathbf {r} \times \mathbf {S} (\mathbf {r} ,t).}$$

Las identidades anteriores son válidas localmente , es decir, en cada punto del espacio en un momento dado . ${\displaystyle \mathbf {r} }$ ${\displaystyle t}$

Momento angular en la naturaleza y el cosmos.

Los ciclones tropicales y otros fenómenos meteorológicos relacionados implican la conservación del momento angular para explicar la dinámica. Los vientos giran lentamente alrededor de los sistemas de baja presión, principalmente debido al efecto coriolis . Si la baja presión se intensifica y el aire que circula lentamente es atraído hacia el centro, las moléculas deben acelerarse para conservar el momento angular. Cuando llegan al centro, las velocidades se vuelven destructivas. ^[2]

Johannes Kepler determinó las leyes del movimiento planetario sin conocer la conservación del momento. Sin embargo, poco después de su descubrimiento, su derivación se determinó a partir de la conservación del momento angular. Los planetas se mueven más lentamente cuanto más se alejan en sus órbitas elípticas, lo que se explica intuitivamente por el hecho de que el momento angular orbital es proporcional al radio de la órbita. Como la masa no cambia y el momento angular se conserva, la velocidad disminuye.

La aceleración de marea es un efecto de las fuerzas de marea entre un satélite natural en órbita (por ejemplo, la Luna ) y el planeta principal que orbita (por ejemplo, la Tierra). El par gravitacional entre la Luna y la marea de la Tierra hace que la Luna sea promovida constantemente a una órbita ligeramente más alta (~3,8 cm por año) y que la Tierra se desacelere (-25,858 ± 0,003″/cy²) en su rotación ( la duración del día aumenta ~1,7 ms por siglo, +2,3 ms por efecto de marea y −0,6 ms por rebote posglacial). La Tierra pierde momento angular que se transfiere a la Luna de modo que se conserva el momento angular general.

Impulso angular en ingeniería y tecnología.

Vídeo: Una herramienta de ejercicio giroscópico es una aplicación de la conservación del momento angular para el fortalecimiento muscular. Una masa que gira rápidamente alrededor de su eje en un dispositivo con forma de bola define un momento angular. Cuando la persona que hace ejercicio inclina la pelota, se produce una fuerza que incluso aumenta la velocidad de rotación cuando el usuario reacciona específicamente.

Abundan los ejemplos del uso de la conservación del momento angular para obtener ventajas prácticas. En motores como los de vapor o los de combustión interna , se necesita un volante para convertir de manera eficiente el movimiento lateral de los pistones en movimiento de rotación.

Los sistemas de navegación inercial utilizan explícitamente el hecho de que el momento angular se conserva con respecto al marco inercial del espacio. La navegación inercial es lo que permite los viajes submarinos bajo la capa de hielo polar, pero también es crucial para todas las formas de navegación moderna.

Las balas estriadas utilizan la estabilidad proporcionada por la conservación del momento angular para ser más fieles en su trayectoria. La invención de las armas de fuego y los cañones estriados dio a sus usuarios una ventaja estratégica significativa en la batalla y, por tanto, supuso un punto de inflexión tecnológico en la historia.

Historia

Isaac Newton , en los Principia , insinuó el momento angular en sus ejemplos de la primera ley del movimiento ,

Una peonza, cuyas partes, por su cohesión, están perpetuamente apartadas de los movimientos rectilíneos, no cesa su rotación, salvo que sea retardada por el aire. Los cuerpos mayores de los planetas y cometas, al encontrar menos resistencia en espacios más libres, conservan sus movimientos tanto progresivos como circulares durante mucho más tiempo. ^[46]

No investigó más a fondo el momento angular directamente en los Principia , diciendo:

De tales reflexiones surgen a veces también los movimientos circulares de los cuerpos alrededor de sus propios centros. Pero estos son casos que no consideraré a continuación; y sería demasiado tedioso demostrar cada detalle que se relaciona con este tema. ^[47]

Sin embargo, su prueba geométrica de la ley de áreas es un ejemplo sobresaliente del genio de Newton y demuestra indirectamente la conservación del momento angular en el caso de una fuerza central .

La ley de las áreas

derivación de Newton

Derivación de Newton de la ley del área utilizando medios geométricos

Cuando un planeta orbita alrededor del Sol , la línea entre el Sol y el planeta barre áreas iguales en intervalos de tiempo iguales. Esto se sabía desde que Kepler expuso su segunda ley del movimiento planetario . Newton obtuvo una prueba geométrica única y demostró que la fuerza de atracción de la gravedad del Sol era la causa de todas las leyes de Kepler.

Durante el primer intervalo de tiempo, un objeto está en movimiento desde el punto A al punto B. Sin ser molestado, continuaría hacia el punto c durante el segundo intervalo. Cuando el objeto llega a B , recibe un impulso dirigido hacia el punto S. El impulso le da una pequeña velocidad adicional hacia S , de modo que si ésta fuera su única velocidad, se movería de B a V durante el segundo intervalo. Según las reglas de composición de velocidades , estas dos velocidades se suman y el punto C se encuentra mediante la construcción del paralelogramo BcCV . Así, el impulso desvía la trayectoria del objeto de modo que llega al punto C al final del segundo intervalo. Como los triángulos SBc y SBC tienen la misma base SB y la misma altura Bc o VC , tienen la misma área. Por simetría, el triángulo SBc también tiene la misma área que el triángulo SAB , por lo tanto el objeto ha barrido áreas iguales SAB y SBC en tiempos iguales.

En el punto C , el objeto recibe otro impulso hacia S , desviando nuevamente su trayectoria durante el tercer intervalo de d a D. Así continúa hasta E y más allá, teniendo los triángulos SAB , SBc , SBC , SCd , SCD , SDe , SDE la misma área. Al permitir que los intervalos de tiempo se hagan cada vez más pequeños, la trayectoria ABCDE se aproxima indefinidamente a una curva continua.

Tenga en cuenta que debido a que esta derivación es geométrica y no se aplica ninguna fuerza específica, demuestra una ley más general que la segunda ley del movimiento planetario de Kepler. Muestra que la Ley de Áreas se aplica a cualquier fuerza central, atractiva o repulsiva, continua o discontinua, o cero.

Conservación del momento angular en la Ley de Áreas

La proporcionalidad del momento angular al área barrida por un objeto en movimiento se puede entender al darse cuenta de que las bases de los triángulos, es decir, las líneas que van desde S al objeto, son equivalentes al radio r, y que las alturas de los Los triángulos son proporcionales a la componente perpendicular de la velocidad v⊥. Por lo tanto, si el área barrida por unidad de tiempo es constante, entonces según la fórmula del área triangular1/2(base)(altura) , el producto (base)(altura) y por tanto el producto rv _⊥ son constantes: si r y la longitud de la base disminuyen, v _⊥ y la altura deben aumentar proporcionalmente. La masa es constante, por lo tanto el momento angular rmv⊥ se conserva mediante este intercambio de distancia y velocidad.

En el caso del triángulo SBC , el área es igual a1/2( SB )( VC ). Dondequiera que finalmente se ubique C debido al impulso aplicado en B , el producto ( SB )( VC ) y, por lo tanto, rmv _⊥ permanecen constantes. Lo mismo ocurre con cada uno de los triángulos.

Otra prueba real de la conservación del impulso para cualquier fuerza central utiliza el teorema de las tangentes amplias de Mamikon. ^{[48] ​​[49]}

Después de Newton

Leonhard Euler , Daniel Bernoulli y Patrick d'Arcy entendieron el momento angular en términos de conservación de la velocidad área , como resultado de su análisis de la segunda ley del movimiento planetario de Kepler. Es poco probable que se dieran cuenta de las implicaciones para la materia en rotación ordinaria. ^[50]

En 1736, Euler, al igual que Newton, abordó algunas de las ecuaciones del momento angular en su Mechanica sin desarrollarlas más. ^[51]

Bernoulli escribió en una carta de 1744 sobre un "momento de movimiento de rotación", posiblemente la primera concepción del momento angular tal como lo entendemos ahora. ^[52]

En 1799, Pierre-Simon Laplace se dio cuenta por primera vez de que un plano fijo estaba asociado con la rotación: su plano invariable .

Louis Poinsot en 1803 comenzó a representar las rotaciones como un segmento de línea perpendicular a la rotación y desarrolló la "conservación de los momentos".

En 1852, Léon Foucault utilizó un giroscopio en un experimento para mostrar la rotación de la Tierra.

El Manual de Mecánica Aplicada de 1858 de William JM Rankine definió por primera vez el momento angular en el sentido moderno:

...una línea cuya longitud es proporcional a la magnitud del momento angular, y cuya dirección es perpendicular al plano de movimiento del cuerpo y al punto fijo, y tal, que cuando el movimiento del cuerpo se ve desde el En el extremo de la línea, el radio-vector del cuerpo parece tener rotación hacia la derecha.

En una edición de 1872 del mismo libro, Rankine afirmó que "El término momento angular fue introducido por el Sr. Hayward", ^[53] probablemente refiriéndose al artículo de RB Hayward Sobre un método directo para estimar velocidades, aceleraciones y todas las cantidades similares con respecto to Axes moveble in any way in Space with Applications, ^[54] que se introdujo en 1856 y se publicó en 1864. Rankine se equivocó, ya que numerosas publicaciones presentan el término desde finales del siglo XVIII hasta principios del XIX. ^[55] Sin embargo, el artículo de Hayward aparentemente fue el primer uso del término y el concepto visto por gran parte del mundo de habla inglesa. Antes de esto, el momento angular se denominaba típicamente "momento de rotación" en inglés. ^[56]

Ver también

• Momento angular absoluto
• Acoplamiento de momento angular
• Momento angular de la luz
• Diagramas de momento angular (mecánica cuántica)
• Rotación caótica
• Coeficientes de Clebsch-Gordan
• Análogos lineales-rotacionales
• Órdenes de magnitud (momento angular)
• Pseudovector de Pauli-Lubanski
• Momento angular relativista
• Rotor rígido
• Energía rotacional
• Momento angular relativo específico
• Yrast

Notas a pie de página

1. En 4 o más dimensiones, el espacio de posibles momentos angulares que puede tener una sola partícula es más limitado.

Referencias

1. "Ciencia elevada: la aerodinámica de volar un disco volador". Científico americano. 9 de agosto de 2012 . Consultado el 4 de enero de 2022 .
2. "Estructura de ciclones tropicales". Servicio Meteorológico Nacional . Consultado el 4 de enero de 2022 .
3. Moore, Thomas (2016). Seis ideas que dieron forma a la física, Unidad C: Las leyes de conservación limitan las interacciones (Tercera ed.). Educación McGraw-Hill. pag. 91.ISBN _ 978-0-07-351394-2.
4. Departamento de Física y Astronomía, Universidad Estatal de Georgia. "Momento de inercia: disco fino". Hiperfísica . Consultado el 17 de marzo de 2023 .
5. Wilson, EB (1915). Momento lineal, energía cinética y momento angular. vol. XXIII. Ginn and Co., Boston, en cooperación con la Universidad de Chicago, et al. pag. 190 - a través de libros de Google. {{cite book}}: |work=ignorado ( ayuda )
6. Worthington, Arthur M. (1906). Dinámica de Rotación. Longmans, Green and Co., Londres. pag. 21 - a través de libros de Google.
7. Taylor, John R. (2005). Mecanica clasica . Libros de ciencias universitarias, Mill Valley, CA. pag. 90.ISBN _ 978-1-891389-22-1.
8. Dadourian, HM (1913). Mecánica Analítica para Estudiantes de Física e Ingeniería. D. Van Nostrand Company, Nueva York. pag. 266 - a través de libros de Google.
9. Watson, W. (1912). Física General. Longmans, Green and Co., Nueva York. pag. 33 - a través de libros de Google.
10. Barker, George F. (1893). Física: Curso Avanzado (4ª ed.). Henry Holt and Company, Nueva York. pag. 66 - a través de Google Books.
11. Barker, George F. (1893). Física: Curso Avanzado (4ª ed.). Henry Holt and Company, Nueva York. págs. 67–68, a través de Google Books.
12. Oberg, Erik; et al. (2000). Manual de maquinaria (26ª ed.). Industrial Press, Inc., Nueva York. pag. 143.ISBN _ 978-0-8311-2625-4.
13. Watson, W. (1912). Física General. Longmans, Green and Co., Nueva York. pag. 34 - a través de libros de Google.
14. Kent, William (1916). El libro de bolsillo de los ingenieros mecánicos (9ª ed.). John Wiley and Sons, Inc., Nueva York. pag. 517 - a través de libros de Google.
15. Oberg, Erik; et al. (2000). Manual de maquinaria (26ª ed.). Industrial Press, Inc., Nueva York. pag. 146.ISBN _ 978-0-8311-2625-4.
16. Oberg, Erik; et al. (2000). Manual de maquinaria (26ª ed.). Industrial Press, Inc., Nueva York. págs. 161-162. ISBN 978-0-8311-2625-4.
17. Kent, William (1916). El libro de bolsillo de los ingenieros mecánicos (9ª ed.). John Wiley and Sons, Inc., Nueva York. pag. 527 - a través de libros de Google.
18. Battin, Richard H. (1999). Introducción a las matemáticas y los métodos de la astrodinámica, edición revisada . Instituto Americano de Aeronáutica y Astronáutica, Inc. ISBN 978-1-56347-342-5., pag. 97
19. Rankine, WJM (1872). Manual de mecánica aplicada (6ª ed.). Charles Griffin and Company, Londres. pag. 507 - a través de libros de Google.
20. Tripulación, Henry (1908). Los principios de la mecánica: para estudiantes de física e ingeniería. Longmans, Green y Company, Nueva York. pag. 88 - a través de libros de Google.
21. Worthington, Arthur M. (1906). Dinámica de Rotación. Longmans, Green and Co., Londres. pag. 82 - a través de libros de Google.
22. Worthington, Arthur M. (1906). Dinámica de Rotación. Longmans, Green and Co., Londres. pag. 11 - a través de libros de Google.
23. Stephenson, FR; Morrison, LV; Whitrow, GJ (1984). "Cambios a largo plazo en la rotación de la Tierra: 700 a. C. a 1980 d. C.". Transacciones filosóficas de la Royal Society . 313 (1524): 47–70. Código Bib : 1984RSPTA.313...47S. doi :10.1098/rsta.1984.0082. S2CID  120566848.+2,40 ms/siglo dividido por 36525 días.
24. Dickey, JO; et al. (1994). "Alcance láser lunar: un legado continuo del programa Apolo" (PDF) . Ciencia . 265 (5171): 482–90, véase 486. Bibcode :1994Sci...265..482D. doi : 10.1126/ciencia.265.5171.482. PMID  17781305. S2CID  10157934. Archivado (PDF) desde el original el 9 de octubre de 2022.
25. Landau, LD; Lifshitz, EM (1995). La teoría clásica de los campos . Curso de Física Teórica. Oxford, Butterworth-Heinemann. ISBN 978-0-7506-2768-9.
26. Tenenbaum, M. y Pollard, H. (1985). Ecuaciones diferenciales ordinarias en un libro de texto elemental para estudiantes de matemáticas. Ingeniería y Ciencias.
27. Ramond, Pierre (2020). Teoría de campo: una introducción moderna (2ª ed.). Rutledge. ISBN 9780429689017.Extracto de la página 1
28. David Morín (2008). Introducción a la mecánica clásica: con problemas y soluciones. Prensa de la Universidad de Cambridge. pag. 311.ISBN _ 978-1-139-46837-4.Extracto de la página 311
29. Battin, Richard H. (1999). Introducción a las matemáticas y los métodos de la astrodinámica, edición revisada . Instituto Americano de Aeronáutica y Astronáutica, Inc. p. 115.ISBN _ 978-1-56347-342-5.
30. Wilson, EB (1915). Momento lineal, energía cinética y momento angular. vol. XXIII. Ginn and Co., Boston, en cooperación con la Universidad de Chicago, et al. pag. 188, ecuación (3) - a través de libros de Google. {{cite book}}: |work=ignorado ( ayuda )
31. Wilson, EB (1915). Momento lineal, energía cinética y momento angular. vol. XXIII. Ginn and Co., Boston, en cooperación con la Universidad de Chicago, et al. pag. 191, Teorema 8 - a través de libros de Google. {{cite book}}: |work=ignorado ( ayuda )
32. Hawking, suroeste; Ellis, GFR (1973). La estructura a gran escala del espacio-tiempo. Prensa de la Universidad de Cambridge. pag. 62–63.
33. Misner, CW; Thorne, KS; Wheeler, JA (1973). "20: Leyes de conservación del momento angular y del 4 momento". Gravitación. WH Freeman y compañía.
34. Synge y Schild, Cálculo tensorial, publicaciones de Dover, edición de 1978, p. 161. ISBN 978-0-486-63612-2 . 
35. de Podestá, Michael (2002). Comprensión de las propiedades de la materia (segunda edición ilustrada y revisada). Prensa CRC. pag. 29.ISBN _ 978-0-415-25788-6.
36. RP Feynman; RB Leighton; M. Arenas (1964). Conferencias de física de Feynman (volumen 2) . Addison-Wesley. págs. 31–7. ISBN 978-0-201-02117-2.
37. Salón 2013 Sección 17.3
38. Veltman, Martinus JG (2018). Hechos y misterios de la física de partículas elementales (edición revisada). Científico mundial. ISBN 978-981-323-707-0.
39. Thaller, Bernd (2005). Mecánica cuántica visual avanzada (edición ilustrada). Medios de ciencia y negocios de Springer. pag. 114.ISBN _ 978-0-387-27127-9.
40. Extraño, Paul (1998). Mecánica cuántica relativista: con aplicaciones en materia condensada y física atómica (edición ilustrada). Prensa de la Universidad de Cambridge. pag. 64.ISBN _ 978-0-521-56583-7.
41. Ballantine, KE; Donegan, JF; Eastham, PR (2016). "Hay muchas formas de hacer girar un fotón: media cuantización de un momento angular óptico total". Avances científicos . 2 (4): e1501748. Código Bib : 2016SciA....2E1748B. doi :10.1126/sciadv.1501748. PMC 5565928 . PMID  28861467. 
42. JH Van Vleck (1951). "El acoplamiento de vectores de momento angular en moléculas". Mod. Rev. Física . 23 (3): 213. Código bibliográfico : 1951RvMP...23..213V. doi :10.1103/RevModPhys.23.213.
43. Littlejohn, Robert (2011). "Apuntes de conferencias sobre rotaciones en mecánica cuántica" (PDF) . Física 221B Primavera de 2011 . Archivado (PDF) desde el original el 9 de octubre de 2022 . Consultado el 13 de enero de 2012 .
44. Okulov, A Yu (2008). "Momento angular de fotones y conjugación de fases". Revista de Física B: Física atómica, molecular y óptica . 41 (10): 101001. arXiv : 0801.2675 . Código Bib : 2008JPhB...41j1001O. doi :10.1088/0953-4075/41/10/101001. S2CID  13307937.
45. Okulov, AY (2008). "Estructuras helicoidales ópticas y sonoras en un espejo Mandelstam - Brillouin". Cartas JETP (en ruso). 88 (8): 561–566. Código Bib : 2008JETPL..88..487O. doi :10.1134/s0021364008200046. S2CID  120371573. Archivado desde el original el 22 de diciembre de 2015 . Consultado el 31 de octubre de 2015 .
46. Newton, Isaac (1803). "Axiomas; o Leyes del Movimiento, Ley I". Los principios matemáticos de la filosofía natural . Andrés Motte, traductor. HD Symonds, Londres. pag. 322 - a través de libros de Google.
47. Newton, Axiomas; o Leyes del movimiento, Corolario III
48. Cruz, LP (2013). "Visual Angular Momentum: Mamikon se encuentra con Kepler". Mensual Matemático Estadounidense . 120 (1): 71–73. doi : 10.4169/amer.math.monthly.120.01.071. S2CID  30994835.
49. Apóstol, Tom M.; Mnatsakanian, Mamikon A. (2012). Nuevos horizontes en geometría . Prensa MAA. págs. 29 y 30. ISBN 978-1-4704-4335-1.
50. ver Borrelli, Arianna (2011). «Impulso angular entre física y matemáticas» (PDF) . Archivado (PDF) desde el original el 9 de octubre de 2022.para obtener un resumen excelente y detallado del concepto de momento angular a lo largo de la historia.
51. Bruce, Ian (2008). "Euler: Mecánica Vol. 1".
52. "Correspondencia de Euler con Daniel Bernoulli, Bernoulli a Euler, 4 de febrero de 1744" (PDF) . El Archivo Euler . Archivado (PDF) desde el original el 9 de octubre de 2022.
53. Rankine, WJM (1872). Manual de mecánica aplicada (6ª ed.). Charles Griffin and Company, Londres. pag. 506 - a través de libros de Google.
54. Hayward, Robert B. (1864). "Sobre un método directo para estimar velocidades, aceleraciones y todas las cantidades similares con respecto a ejes móviles de cualquier forma en el espacio con aplicaciones". Transacciones de la Sociedad Filosófica de Cambridge . 10 : 1. Código Bib : 1864TCaPS..10....1H.
55. ver, por ejemplo, Gompertz, Benjamin (1818). "Sobre péndulos que vibran entre las mejillas". La Revista de Ciencias y Artes . III (V): 17 - a través de libros de Google.; Herapath, Juan (1847). Física Matemática. Whittaker and Co., Londres. pag. 56 - a través de libros de Google.
56. ver, por ejemplo, Landen, John (1785). "Del movimiento giratorio de un cuerpo de cualquier forma". Transacciones filosóficas . LXXV (I): 311–332. doi :10.1098/rstl.1785.0016. S2CID  186212814.

Otras lecturas

• Cohen-Tannoudji, Claude; Diu, Bernardo; Laloë, Franck (2006). Mecánica cuántica (edición de 2 volúmenes). John Wiley e hijos. ISBN 978-0-471-56952-7.
• Condón, UE; Shortley, GH (1935). "Especialmente el Capítulo 3". La teoría de los espectros atómicos . Prensa de la Universidad de Cambridge. ISBN 978-0-521-09209-8.
• Edmonds, AR (1957). Momento angular en mecánica cuántica . Prensa de la Universidad de Princeton. ISBN 978-0-691-07912-7.
• Hall, Brian C. (2013), Teoría cuántica para matemáticos , Textos de posgrado en matemáticas, vol. 267, Springer, Bibcode : 2013qtm..libro.....H, ISBN 978-0-387-40122-5.
• Jackson, John David (1998). Electrodinámica clásica (3ª ed.). John Wiley e hijos. ISBN 978-0-471-30932-1.
• Serway, Raymond A.; Jewett, John W. (2004). Física para científicos e ingenieros (6ª ed.). Brooks/Cole. ISBN 978-0-534-40842-8.
• Thompson, William J. (1994). Momento angular: una guía ilustrada sobre simetrías rotacionales para sistemas físicos . Wiley. ISBN 978-0-471-55264-2.
• Tipler, Paul (2004). Física para científicos e ingenieros: mecánica, oscilaciones y ondas, termodinámica (5ª ed.). WH Freeman. ISBN 978-0-7167-0809-4.
• Feynman R ; Leighton R ; Sands M (septiembre de 2013). "19–4 Energía cinética rotacional". The Feynman Lectures on Physics (edición en línea) - a través del sitio web de The Feynman Lectures.

enlaces externos

• "¿Qué tienen en común un submarino, un cohete y una pelota de fútbol? Por qué el esferoide alargado es la forma del éxito" ( Scientific American , 8 de noviembre de 2010)
• Conservación del momento angular Archivado el 7 de diciembre de 2016 en Wayback Machine : un capítulo de un libro de texto en línea
• Momento angular en un proceso de colisión: derivación del caso tridimensional
• Momento angular y movimiento rodante: más teoría del impulso