Elementos orbitales

Los elementos orbitales son los parámetros necesarios para identificar de forma única una órbita específica . En mecánica celeste estos elementos se consideran en sistemas de dos cuerpos utilizando una órbita de Kepler . Hay muchas formas diferentes de describir matemáticamente la misma órbita, pero ciertos esquemas, cada uno de los cuales consta de un conjunto de seis parámetros, se utilizan comúnmente en astronomía y mecánica orbital .

Una órbita real y sus elementos cambian con el tiempo debido a perturbaciones gravitacionales de otros objetos y a los efectos de la relatividad general . Una órbita de Kepler es una aproximación matemática idealizada de la órbita en un momento particular.

elementos keplerianos

En este diagrama, el plano orbital (amarillo) intersecta un plano de referencia (gris). Para los satélites en órbita terrestre, el plano de referencia suele ser el plano ecuatorial de la Tierra, y para los satélites en órbitas solares es el plano de la eclíptica . La intersección se llama línea de nodos , ya que conecta el centro de masa con los nodos ascendentes y descendentes. El plano de referencia, junto con el punto vernal ( ♈︎ ), establece un marco de referencia.

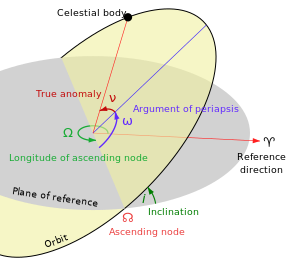
Los elementos orbitales tradicionales son los seis elementos keplerianos , según Johannes Kepler y sus leyes del movimiento planetario .

Cuando se ven desde un marco inercial , dos cuerpos en órbita trazan trayectorias distintas. Cada una de estas trayectorias tiene su foco en el centro de masa común . Cuando se ve desde un marco no inercial centrado en uno de los cuerpos, sólo es aparente la trayectoria del cuerpo opuesto; Los elementos keplerianos describen estas trayectorias no inerciales. Una órbita tiene dos conjuntos de elementos keplerianos dependiendo del cuerpo que se utilice como punto de referencia. El cuerpo de referencia (normalmente el más masivo) se denomina primario , el otro cuerpo se denomina secundario . El primario no necesariamente posee más masa que el secundario, e incluso cuando los cuerpos son de igual masa, los elementos orbitales dependen de la elección del primario.

Dos elementos definen la forma y el tamaño de la elipse:

Excentricidad ( $e$ ): forma de la elipse, que describe cuánto se alarga en comparación con un círculo (no marcada en el diagrama).
Semieje mayor ( $a$ ): la suma de las distancias de periapsis y apoapsis dividida por dos. Para las órbitas clásicas de dos cuerpos, el semieje mayor es la distancia entre los centros de los cuerpos, no la distancia de los cuerpos al centro de masa.

Dos elementos definen la orientación del plano orbital en el que está incrustada la elipse:

Inclinación ( $i$ ) — inclinación vertical de la elipse con respecto al plano de referencia, medida en el nodo ascendente (donde la órbita pasa hacia arriba a través del plano de referencia, el ángulo $i$ verde en el diagrama). El ángulo de inclinación se mide perpendicular a la línea de intersección entre el plano orbital y el plano de referencia. Tres puntos distintos en una elipse definirán el plano orbital de la elipse. El plano y la elipse son objetos bidimensionales definidos en un espacio tridimensional.
Longitud del nodo ascendente ( $Ω$ ): orienta horizontalmente el nodo ascendente de la elipse (donde la órbita pasa de sur a norte a través del plano de referencia, simbolizado por $☊$ ) con respecto al punto primaveral del sistema de referencia (simbolizado por ♈︎). Esto se mide en el plano de referencia y se muestra como el ángulo verde $Ω$ en el diagrama.

Los dos elementos restantes son los siguientes:

El argumento de periapsis ( $ω$ ) define la orientación de la elipse en el plano orbital, como un ángulo medido desde el nodo ascendente hasta el periapsis (el punto más cercano al objeto satélite del objeto primario alrededor del cual orbita), el ángulo violeta $ω$ en el diagrama.
La verdadera anomalía ( $ν$ , $θ$ o $f$ ) en la época ( $t 0$ ) define la posición del cuerpo en órbita a lo largo de la elipse en un momento específico (la "época").

La anomalía media $M$ es un "ángulo" ficticio matemáticamente conveniente que varía linealmente con el tiempo, pero que no corresponde a un ángulo geométrico real. Se puede convertir en la verdadera anomalía $ν$ , que representa el ángulo geométrico real en el plano de la elipse, entre la periapsis (la aproximación más cercana al cuerpo central) y la posición del objeto en órbita en un momento dado. Por lo tanto, la verdadera anomalía se muestra como el ángulo rojo $ν$ en el diagrama y la anomalía media no se muestra.

Los ángulos de inclinación, la longitud del nodo ascendente y el argumento del periapsis también pueden describirse como los ángulos de Euler que definen la orientación de la órbita con respecto al sistema de coordenadas de referencia.

Tenga en cuenta que también existen trayectorias no elípticas, pero no están cerradas y, por tanto, no son órbitas. Si la excentricidad es mayor que uno, la trayectoria es una hipérbola . Si la excentricidad es igual a uno y el momento angular es cero, la trayectoria es radial . Si la excentricidad es uno y hay momento angular, la trayectoria es una parábola .

Parámetros requeridos

Dado un marco de referencia inercial y una época arbitraria (un punto específico en el tiempo), se necesitan exactamente seis parámetros para definir inequívocamente una órbita arbitraria y no perturbada.

Esto se debe a que el problema contiene seis grados de libertad . Estos corresponden a las tres dimensiones espaciales que definen la posición ( $x$ , $y$ , $z$ en un sistema de coordenadas cartesiano ), más la velocidad en cada una de estas dimensiones. Estos pueden describirse como vectores de estado orbital , pero esta suele ser una forma inconveniente de representar una órbita, razón por la cual se utilizan comúnmente elementos keplerianos en su lugar.

A veces, la época se considera un "séptimo" parámetro orbital, en lugar de parte del marco de referencia.

Si se define que la época es el momento en que uno de los elementos es cero, el número de elementos no especificados se reduce a cinco. (El sexto parámetro todavía es necesario para definir la órbita; simplemente se establece numéricamente en cero por convención o se "mueve" a la definición de época con respecto al tiempo del reloj del mundo real).

Parametrizaciones alternativas

Los elementos keplerianos se pueden obtener a partir de vectores de estado orbital (un vector tridimensional para la posición y otro para la velocidad) mediante transformaciones manuales o con software informático. ^[1]

Se pueden calcular otros parámetros orbitales a partir de los elementos keplerianos, como el período , la apoapsis y la periapsis . (Cuando se orbita la Tierra, los dos últimos términos se conocen como apogeo y perigeo). Es común especificar el período en lugar del semieje mayor en los conjuntos de elementos keplerianos, ya que cada uno puede calcularse a partir del otro siempre que la gravedad gravitacional estándar. El parámetro $GM$ se proporciona para el cuerpo central.

En lugar de la anomalía media en la época , se podría utilizar la anomalía media $M$ , la longitud media , la anomalía verdadera $ν 0$ o (raramente) la anomalía excéntrica .

Usar, por ejemplo, la "anomalía media" en lugar de "anomalía media en la época" significa que el tiempo $t$ debe especificarse como un séptimo elemento orbital. A veces se supone que la anomalía media es cero en la época (eligiendo la definición apropiada de la época), dejando solo los otros cinco elementos orbitales por especificar.

Se utilizan diferentes conjuntos de elementos para distintos cuerpos astronómicos. La excentricidad, $e$ , y el semieje mayor, $a$ , o la distancia del periapsis, $q$ , se utilizan para especificar la forma y el tamaño de una órbita. La longitud del nodo ascendente, $Ω$ , la inclinación, $i$ , y el argumento de la periapsis, $ω$ , o la longitud de la periapsis, $ϖ$ , especifican la orientación de la órbita en su plano. Para especificar un punto conocido en la órbita se utilizan la longitud en la época, $L 0$ , la anomalía media en la época, $M 0$ , o el tiempo de paso del perihelio, $T 0 .$ Las elecciones que se hagan dependen de si se utiliza el equinoccio de primavera o el nodo como referencia principal. El semieje mayor se conoce si se conocen el movimiento medio y la masa gravitacional . ^[2]^[3]

También es bastante común ver la anomalía media ( $M$ ) o la longitud media ( $L$ ) expresadas directamente, sin $M 0$ o $L 0$ como pasos intermedios, como una función polinómica con respecto al tiempo. Este método de expresión consolidará el movimiento medio ( $n$ ) en el polinomio como uno de los coeficientes. Parecerá que $L$ o $M$ se expresan de una manera más complicada, pero parecerá que necesitaremos un elemento orbital menos.

El movimiento medio también puede quedar oculto detrás de citas del período orbital $P.$ ^{[ se necesita aclaración ]}

Transformaciones de ángulos de Euler

Los ángulos $Ω$ , $i$ , $ω$ son los ángulos de Euler (correspondientes a $α$ , $β$ , $γ$ en la notación utilizada en ese artículo) que caracterizan la orientación del sistema de coordenadas.

$x̂$ , $ŷ$ , $ẑ$ del sistema de coordenadas inercial $Î$ , $Ĵ$ , $K̂$

dónde:

$Î$ , $Ĵ$ está en el plano ecuatorial del cuerpo central. $Î$ está en la dirección del equinoccio de primavera. $Ĵ$ es perpendicular a $Î$ y con $Î$ define el plano de referencia. $K̂$ es perpendicular al plano de referencia. Los elementos orbitales de los cuerpos (planetas, cometas, asteroides,...) del Sistema Solar suelen ser la eclíptica como ese plano.
$x̂$ , $ŷ$ están en el plano orbital y con $x̂$ en dirección al pericentro ( periapsis ). $ẑ$ es perpendicular al plano de la órbita. $ŷ$ es mutuamente perpendicular a $x̂$ y $ẑ$ .

Entonces, la transformación del marco de coordenadas $Î$ , $Ĵ$ , $K̂$ al marco $x̂$ , $ŷ$ , $ẑ$ con los ángulos de Euler $Ω$ , $i$ , $ω$ es:

{\begin{aligned}x_{1}&=\cos \Omega \cdot \cos \omega -\sin \Omega \cdot \cos i\cdot \sin \omega \ ;\\x_{2}&=\sin \Omega \cdot \cos \omega +\cos \Omega \cdot \cos i\cdot \sin \omega \ ;\\x_{3}&=\sin i\cdot \sin \omega ;\\\,\\y_{1}&=-\cos \Omega \cdot \sin \omega -\sin \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{2}&=-\sin \Omega \cdot \sin \omega +\cos \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{3}&=\sin i\cdot \cos \omega \ ;\\\,\\z_{1}&=\sin i\cdot \sin \Omega \ ;\\z_{2}&=-\sin i\cdot \cos \Omega \ ;\\z_{3}&=\cos i\ ;\\\end{aligned}}

{\begin{bmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\z_{1}&z_{2}&z_{3}\end{bmatrix}}={\begin{bmatrix}\cos \omega &\sin \omega &0\\-\sin \omega &\cos \omega &0\\0&0&1\end{bmatrix}}\,{\begin{bmatrix}1&0&0\\0&\cos i&\sin i\\0&-\sin i&\cos i\end{bmatrix}}\,{\begin{bmatrix}\cos \Omega &\sin \Omega &0\\-\sin \Omega &\cos \Omega &0\\0&0&1\end{bmatrix}}\,;

{\begin{aligned}\mathbf {\hat {x}} &=x_{1}\mathbf {\hat {I}} +x_{2}\mathbf {\hat {J}} +x_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {y}} &=y_{1}\mathbf {\hat {I}} +y_{2}\mathbf {\hat {J}} +y_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {z}} &=z_{1}\mathbf {\hat {I}} +z_{2}\mathbf {\hat {J}} +z_{3}\mathbf {\hat {K}} ~.\\\end{aligned}}

La transformación inversa, que calcula las 3 coordenadas en el sistema IJK dadas las 3 (o 2) coordenadas en el sistema xyz, está representada por la matriz inversa. Según las reglas del álgebra matricial , la matriz inversa del producto de las 3 matrices de rotación se obtiene invirtiendo el orden de las tres matrices y cambiando los signos de los tres ángulos de Euler.

La transformación de $x̂$ , $ŷ$ , $ẑ$ a los ángulos de Euler $Ω$ , $i$ , $ω$ es:

{\begin{aligned}\Omega &=\operatorname {arg} \left(-z_{2},z_{1}\right)\\i&=\operatorname {arg} \left(z_{3},{\sqrt {{z_{1}}^{2}+{z_{2}}^{2}}}\right)\\\omega &=\operatorname {arg} \left(y_{3},x_{3}\right)\\\end{aligned}}

arg(x, y)

atan2(y,x)

Predicción de órbita

En condiciones ideales de un cuerpo central perfectamente esférico, cero perturbaciones y efectos relativistas insignificantes, todos los elementos orbitales, excepto la anomalía media, son constantes. La anomalía media cambia linealmente con el tiempo, escalada por el movimiento medio , ^[2]

n={\sqrt {\frac {\mu }{a^{3}}}}.

μ

parámetro gravitacional estándar

t 0

(e 0, a 0, i 0, Ω 0, ω 0, M 0)

t = t 0 + δt

(e 0, a 0, yo 0, Ω 0, ω 0, M 0 + norte δt)

Perturbaciones y varianza elemental.

Las órbitas newtonianas de dos cuerpos , imperturbadas , son siempre secciones cónicas , por lo que los elementos keplerianos definen una elipse , una parábola o una hipérbola . Las órbitas reales tienen perturbaciones, por lo que un conjunto dado de elementos keplerianos describe con precisión una órbita sólo en la época. La evolución de los elementos orbitales se produce debido a la atracción gravitacional de los cuerpos distintos del primario, la no esfericidad del primario, la resistencia atmosférica , los efectos relativistas , la presión de la radiación , las fuerzas electromagnéticas , etc.

Los elementos keplerianos a menudo se pueden utilizar para producir predicciones útiles en momentos cercanos a la época. Alternativamente, las trayectorias reales se pueden modelar como una secuencia de órbitas keplerianas que osculan ("besan" o tocan) la trayectoria real. También pueden describirse mediante las llamadas ecuaciones planetarias, ecuaciones diferenciales que se presentan en diferentes formas desarrolladas por Lagrange , Gauss , Delaunay , Poincaré o Hill .

Elementos de dos líneas

Los parámetros de los elementos keplerianos se pueden codificar como texto en varios formatos. El más común de ellos es el formato de "elementos de dos líneas" (TLE) de NASA / NORAD , ^[4] diseñado originalmente para usarse con tarjetas perforadas de 80 columnas, pero todavía en uso porque es el formato más común y puede manejarse fácilmente por todos los almacenamientos de datos modernos también.

Dependiendo de la aplicación y la órbita del objeto, los datos derivados de TLE de más de 30 días pueden volverse poco fiables. Las posiciones orbitales se pueden calcular a partir de TLE mediante los algoritmos SGP/ SGP4 / SDP4 /SGP8/SDP8. ^[5]

Ejemplo de un elemento de dos líneas: ^[6]

1 27651U 03004A 07083.49636287 .00000119 00000-0 30706-4 0 26922 27651 039.9951 132.2059 0025931 073.4582 286.9047 14.81909376225249

variables delaunay

Los elementos orbitales de Delaunay fueron introducidos por Charles-Eugène Delaunay durante su estudio del movimiento de la Luna . ^[7] Comúnmente llamadas variables de Delaunay , son un conjunto de variables canónicas , que son coordenadas de ángulo de acción . Los ángulos son sumas simples de algunos de los ángulos de Kepler:

la longitud media : $\ell =M+\omega +\Omega \,,$
la longitud del periapsis : y $g=\omega +\Omega \,,$
la longitud del nodo ascendente : $h=\Omega$

junto con sus respectivos momentos conjugados , $L$ , $G$ y $H.$ ^[8] Los momentos $L$ , $G$ y $H$ son las variables de acción y son combinaciones más elaboradas de los elementos keplerianos $a$ , $e$ e $i$ .

Las variables de Delaunay se utilizan para simplificar los cálculos perturbativos en mecánica celeste, por ejemplo, al investigar las oscilaciones de Kozai-Lidov en sistemas triples jerárquicos. ^[8] La ventaja de las variables de Delaunay es que permanecen bien definidas y no singulares (excepto $h$ , que puede ser tolerado) cuando $e$ y/o $i$ son muy pequeños: cuando la órbita de la partícula de prueba es casi circular ( ) , o casi “plano” ( ). $e\approx 0$ $i\approx 0$

Ver también

Referencias

^ Por ejemplo, con "VEC2TLE". amsat.org . Archivado desde el original el 20 de mayo de 2016 . Consultado el 19 de junio de 2013 .
^ ab Green, Robin M. (1985). Astronomía Esférica . Prensa de la Universidad de Cambridge. ISBN 978-0-521-23988-2.
^ Danby, JMA (1962). Fundamentos de la Mecánica Celeste . Willmann-Bell. ISBN 978-0-943396-20-0.
^ Kelso, TS "Preguntas frecuentes: formato de conjunto de elementos de dos líneas". celestrak.com . CelesTrak. Archivado desde el original el 26 de marzo de 2016 . Consultado el 15 de junio de 2016 .
^ Seidelmann, KP, ed. (1992). Suplemento explicativo del Almanaque astronómico (1ª ed.). Mill Valley, CA: Libros de ciencias universitarias.
^ "FUENTE". Cielos-Above.com . datos de la órbita. Archivado desde el original el 27 de septiembre de 2007.
^ Aubin, David (2014). "Delaunay, Charles-Eugène". Enciclopedia biográfica de astrónomos . Nueva York, Nueva York: Springer Nueva York. págs. 548–549. doi :10.1007/978-1-4419-9917-7_347. ISBN 978-1-4419-9916-0.
^ ab Shevchenko, Ivan (2017). El efecto Lidov-Kozai: aplicaciones en la investigación de exoplanetas y astronomía dinámica . Cham: Springer. ISBN 978-3-319-43522-0.

enlaces externos

Gurfil, Pini (2005). "Parámetros de Euler como elementos orbitales no singulares en órbitas casi ecuatoriales". J. Guid. Control. Dinámica . 28 (5): 1079–1084. Código Bib : 2005JGCD...28.1079G. doi :10.2514/1.14760.

Wikilibros tiene un libro sobre el tema: Astrodinámica/Elementos de órbita clásicos

"Tutorial". AMSAT . Elementos keplerianos. Archivado desde el original el 14 de octubre de 2002.

"Tutorial de órbitas". marine.rutgers.edu . Archivado desde el original el 19 de abril de 2021 . Consultado el 30 de julio de 2019 .

"Visualizador de elementos orbitales". orbitalmechanics.info .

Informe nº 3 (PDF) . celestrak (Reporte). Pista espacial. Comando de Defensa Aeroespacial de América del Norte (NORAD). Archivado (PDF) desde el original el 3 de septiembre de 2000.– un tratamiento serio de los elementos orbitales

"PREGUNTAS MÁS FRECUENTES". Celestrak . Elementos de dos líneas. Archivado desde el original el 26 de marzo de 2016.

"Las efemérides en línea de JPL HORIZONS".– también proporciona elementos orbitales para una gran cantidad de objetos del sistema solar

"Parámetros orbitales medios". ssd.jpl.nasa.gov . Satélites planetarios. JPL/NASA.

"Introducción a la exportación". ssd.jpl.nasa.gov . Efemérides planetarias y lunares del JPL. JPL/NASA.

"Vectores de estado: VEC2TLE". MindSpring (software). Archivado desde el original el 3 de marzo de 2016.– acceso al software VEC2TLE

"Función 'iauPlan94'" ( fuente del software C ). Biblioteca IAU SOFA C.– elementos orbitales de los planetas principales