Anomalía media

Especifica la órbita de un objeto en el espacio.

Área barrida por unidad de tiempo  por un objeto en una órbita elíptica , y  por un objeto imaginario en una órbita circular (con el mismo período orbital). Ambos barren áreas iguales en tiempos iguales, pero la velocidad angular de barrido varía para la órbita elíptica y es constante para la órbita circular. Se muestran la anomalía media y la anomalía verdadera para dos unidades de tiempo. (Tenga en cuenta que para simplificar visualmente, se diagrama una órbita circular que no se superpone, por lo tanto, esta órbita circular con el mismo período orbital no se muestra en escala real con esta órbita elíptica: para que la escala sea verdadera para las dos órbitas de período igual, estas órbitas deben intersecarse).

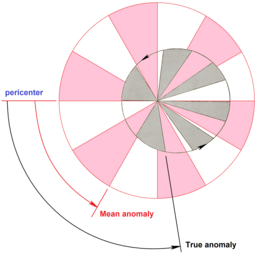
En mecánica celeste , la anomalía media es la fracción del período de una órbita elíptica que ha transcurrido desde que el cuerpo en órbita pasó por el periapsis , expresada como un ángulo que puede usarse para calcular la posición de ese cuerpo en el problema clásico de los dos cuerpos . Es la distancia angular desde el pericentro que tendría un cuerpo ficticio si se moviera en una órbita circular , con velocidad constante , en el mismo período orbital que el cuerpo real en su órbita elíptica. ^{[1] [2]}

Definición

Defina T como el tiempo que necesita un cuerpo en particular para completar una órbita. En el tiempo T , el radio vector recorre 2 π radianes, o 360°. La velocidad media de barrido, n , es entonces

$${\displaystyle n={\frac {\,2\,\pi \,}{T}}={\frac {\,360^{\circ }\,}{T}}~,}$$

que se llama movimiento angular medio del cuerpo, con dimensiones de radianes por unidad de tiempo o grados por unidad de tiempo.

Defina τ como el tiempo en el que el cuerpo se encuentra en el pericentro. A partir de las definiciones anteriores, se puede definir una nueva cantidad, M , la anomalía media .

$${\displaystyle M=n\,(t-\tau )~,}$$

que da una distancia angular desde el pericentro en un tiempo arbitrario t ^[3] con dimensiones de radianes o grados.

Como la tasa de aumento, n , es un promedio constante, la anomalía media aumenta uniformemente (linealmente) de 0 a 2 π radianes o de 0° a 360° durante cada órbita. Es igual a 0 cuando el cuerpo está en el pericentro, π radianes (180°) en el apocentro y 2 π radianes (360°) después de una revolución completa. ^[4] Si la anomalía media se conoce en un instante dado, se puede calcular en cualquier instante posterior (o anterior) simplemente sumando (o restando) n⋅δt donde δt representa la pequeña diferencia de tiempo.

La anomalía media no mide un ángulo entre objetos físicos (excepto en el pericentro o el apocentro, o en una órbita circular). Es simplemente una medida uniforme y conveniente de cuánto ha progresado un cuerpo alrededor de su órbita desde el pericentro. La anomalía media es uno de los tres parámetros angulares (conocidos históricamente como "anomalías") que definen una posición a lo largo de una órbita; los otros dos son la anomalía excéntrica y la anomalía verdadera .

Anomalía media en la época

La anomalía media en la época , M ₀ , se define como la anomalía media instantánea en una época dada , t ₀ . Este valor a veces se proporciona con otros elementos orbitales para permitir cálculos de las posiciones pasadas y futuras del objeto a lo largo de la órbita. La época para la que se define M ₀ a menudo se determina por convención en un campo o disciplina determinados. Por ejemplo, las efemérides planetarias a menudo definen M ₀ para la época J2000 , mientras que para los objetos que orbitan la Tierra descritos por un conjunto de elementos de dos líneas, la época se especifica como una fecha en la primera línea. ^[5]

Fórmulas

La anomalía media M se puede calcular a partir de la anomalía excéntrica E y la excentricidad e con la ecuación de Kepler :

$${\displaystyle M=E-e\,\sin E~.}$$

La anomalía media también se observa con frecuencia como

$${\displaystyle M=M_{0}+n\left(t-t_{0}\right)~,}$$

donde M ₀ es la anomalía media en la época t ₀ , que puede coincidir o no con τ , el momento del paso por el pericentro. El método clásico para hallar la posición de un objeto en una órbita elíptica a partir de un conjunto de elementos orbitales consiste en calcular la anomalía media mediante esta ecuación y, a continuación, resolver la ecuación de Kepler para la anomalía excéntrica.

Defina ϖ como la longitud del pericentro , la distancia angular del pericentro desde una dirección de referencia. Defina ℓ como la longitud media , la distancia angular del cuerpo desde la misma dirección de referencia, suponiendo que se mueve con un movimiento angular uniforme como con la anomalía media. Por lo tanto, la anomalía media también es ^[6]

$${\displaystyle M=\ell -\varpi ~.}$$

El movimiento angular medio también se puede expresar,

$${\displaystyle n={\sqrt {{\frac {\mu }{\;a^{3}\,}}\,}}~,}$$

donde μ es el parámetro gravitacional , que varía con las masas de los objetos, y a es el semieje mayor de la órbita. La anomalía media puede entonces expandirse,

$${\displaystyle M={\sqrt {{\frac {\mu }{\;a^{3}\,}}\,}}\,\left(t-\tau \right)~,}$$

y aquí la anomalía media representa un movimiento angular uniforme en un círculo de radio a . ^[7]

La anomalía media se puede calcular a partir de la excentricidad y la anomalía verdadera f hallando la anomalía excéntrica y luego utilizando la ecuación de Kepler. Esto da, en radianes: donde atan2 (y, x) es el ángulo desde el eje x del rayo de (0, 0) a (x, y), que tiene el mismo signo que y. $${\displaystyle M=\operatorname {atan2} \left(-\ {\sqrt {1-e^{2}}}\sin f,-\ e-\cos f\right)+\pi -e{\frac {{\sqrt {1-e^{2}}}\sin f}{1+e\cos f}}}$$

En el caso de las trayectorias parabólicas e hiperbólicas, la anomalía media no está definida, porque no tienen período. Pero en esos casos, como en el caso de las órbitas elípticas, el área barrida por una cuerda entre el atractor y el objeto que sigue la trayectoria aumenta linealmente con el tiempo. Para el caso hiperbólico, existe una fórmula similar a la anterior que da el tiempo transcurrido en función del ángulo (la anomalía verdadera en el caso elíptico), como se explica en el artículo Órbita de Kepler . Para el caso parabólico, existe una fórmula diferente, el caso límite tanto para el caso elíptico como para el hiperbólico, ya que la distancia entre los focos tiende al infinito (véase Trayectoria parabólica#Ecuación de Barker) .

La anomalía media también puede expresarse como una expansión en serie : ^[8] $${\displaystyle M=f+2\sum _{n=1}^{\infty }(-1)^{n}\left[{\frac {1}{n}}+{\sqrt {1-e^{2}}}\right]\beta ^{n}\sin {nf}}$$

con ${\displaystyle \beta ={\frac {1-{\sqrt {1-e^{2}}}}{e}}}$

$${\displaystyle M=f-2\,e\sin f+\left({\frac {3}{4}}e^{2}+{\frac {1}{8}}e^{4}\right)\sin 2f-{\frac {1}{3}}e^{3}\sin 3f+{\frac {5}{32}}e^{4}\sin 4f+\operatorname {\mathcal {O}} \left(e^{5}\right)}$$

Una fórmula similar proporciona la anomalía verdadera directamente en términos de la anomalía media: ^[9]

$${\displaystyle f=M+\left(2\,e-{\frac {1}{4}}e^{3}\right)\sin M+{\frac {5}{4}}e^{2}\sin 2M+{\frac {13}{12}}e^{3}\sin 3M+\operatorname {\mathcal {O}} \left(e^{4}\right)}$$

Una formulación general de la ecuación anterior se puede escribir como la ecuación del centro : ^[10]

$${\displaystyle f=M+2\sum _{s=1}^{\infty }{\frac {1}{s}}\left[J_{s}(se)+\sum _{p=1}^{\infty }\beta ^{p}{\big (}J_{s-p}(se)+J_{s+p}(se){\big )}\right]\sin(sM)}$$

Véase también

• Leyes de Kepler sobre el movimiento planetario
• Longitud media
• Movimiento medio
• Elementos orbitales

Referencias

1. Montenbruck, Oliver (1989). Cálculos prácticos de efemérides . Springer-Verlag . pág. 44. ISBN. 0-387-50704-3.
2. Meeus, Jean (1991). Algoritmos astronómicos . Willmann-Bell, Inc., Richmond, VA. pag. 182.ISBN​ 0-943396-35-2.
3. Smart, WM (1977). Libro de texto sobre astronomía esférica (sexta edición). Cambridge University Press, Cambridge. pág. 113. ISBN 0-521-29180-1.
4. Meeus (1991), pág. 183
5. "Space-Track.org". www.space-track.org . Consultado el 19 de agosto de 2024 .
6. Smart (1977), pág. 122
7. Vallado, David A. (2001). Fundamentos de astrodinámica y aplicaciones (2.ª ed.). El Segundo, California: Microcosm Press. pp. 53–54. ISBN 1-881883-12-4.
8. Smart, WM (1953). Mecánica celeste . Londres, Reino Unido: Longmans, Green, and Co., pág. 38.
9. Roy, AE (1988). Movimiento orbital (1.ª ed.). Bristol, Reino Unido; Filadelfia, Pensilvania: A. Hilger. ISBN 0852743602.
10. Brouwer, Dirk (1961). Métodos de mecánica celeste . Elsevier. págs. 77 y siguientes.

Enlaces externos

• Entrada del glosario anomalía, media Archivado el 23 de diciembre de 2017 en Wayback Machine en el Almanaque Astronómico en Línea del Observatorio Naval de los EE. UU. Archivado el 20 de abril de 2015 en Wayback Machine