Geometría diferencial de superficies

Las matemáticas de las superficies lisas

Carl Friedrich Gauss en 1828

En matemáticas , la geometría diferencial de superficies se ocupa de la geometría diferencial de superficies lisas ^[a] con varias estructuras adicionales, más frecuentemente, una métrica de Riemann . ^[b]

Las superficies han sido estudiadas extensamente desde varias perspectivas: extrínsecamente , en relación con su incrustación en el espacio euclidiano e intrínsecamente , reflejando sus propiedades determinadas únicamente por la distancia dentro de la superficie medida a lo largo de las curvas de la superficie. Uno de los conceptos fundamentales investigados es la curvatura gaussiana , estudiada en profundidad por primera vez por Carl Friedrich Gauss , ^[1] quien demostró que la curvatura era una propiedad intrínseca de una superficie, independiente de su incrustación isométrica en el espacio euclidiano.

Las superficies surgen naturalmente como gráficos de funciones de un par de variables , y a veces aparecen en forma paramétrica o como lugares geométricos asociados a curvas espaciales . Un papel importante en su estudio lo han desempeñado los grupos de Lie (en el espíritu del programa de Erlangen ), a saber, los grupos de simetría del plano euclidiano , la esfera y el plano hiperbólico . Estos grupos de Lie se pueden utilizar para describir superficies de curvatura gaussiana constante; también proporcionan un ingrediente esencial en el enfoque moderno de la geometría diferencial intrínseca a través de conexiones . Por otro lado, las propiedades extrínsecas que dependen de una incrustación de una superficie en el espacio euclidiano también se han estudiado ampliamente. Esto está bien ilustrado por las ecuaciones no lineales de Euler-Lagrange en el cálculo de variaciones : aunque Euler desarrolló las ecuaciones de una variable para comprender las geodésicas , definidas independientemente de una incrustación, una de las principales aplicaciones de Lagrange de las ecuaciones de dos variables fue a las superficies mínimas , un concepto que solo se puede definir en términos de una incrustación.

Historia

Bernhard Riemann (1826-1866)

Los volúmenes de ciertas superficies cuadráticas de revolución fueron calculados por Arquímedes . ^[2] El desarrollo del cálculo en el siglo XVII proporcionó una forma más sistemática de calcularlos. ^[3] La curvatura de superficies generales fue estudiada por primera vez por Euler . En 1760 ^[4] demostró una fórmula para la curvatura de una sección plana de una superficie y en 1771 ^[5] consideró superficies representadas en forma paramétrica. Monge sentó las bases de su teoría en su memoria clásica L'application de l'analyse à la géometrie que apareció en 1795. La contribución definitoria a la teoría de superficies fue hecha por Gauss en dos artículos notables escritos en 1825 y 1827. ^[1] Esto marcó un nuevo alejamiento de la tradición porque por primera vez Gauss consideró la geometría intrínseca de una superficie, las propiedades que están determinadas solo por las distancias geodésicas entre puntos en la superficie independientemente de la forma particular en que la superficie está ubicada en el espacio euclidiano ambiental. El resultado culminante, el Theorema Egregium de Gauss, estableció que la curvatura gaussiana es un invariante intrínseco, es decir, invariante bajo isometrías locales . Este punto de vista fue extendido a espacios de dimensiones superiores por Riemann y condujo a lo que hoy se conoce como geometría riemanniana . El siglo XIX fue la época dorada de la teoría de superficies, tanto desde el punto de vista topológico como desde el punto de vista geométrico-diferencial, y la mayoría de los geómetras más destacados se dedicaron a su estudio. ^{[ cita requerida ]} Darboux recopiló muchos resultados en su tratado de cuatro volúmenes Théorie des surface (1887-1896).

Descripción general

Resulta intuitivamente bastante familiar decir que la hoja de una planta, la superficie de un vaso o la forma de una cara están curvadas de determinadas maneras y que todas estas formas, incluso después de ignorar cualquier marca distintiva, tienen ciertas características geométricas que las distinguen unas de otras. La geometría diferencial de superficies se ocupa de una comprensión matemática de tales fenómenos. El estudio de este campo, que se inició en su forma moderna en el siglo XVIII, ha llevado al desarrollo de la geometría abstracta y de dimensiones superiores, como la geometría de Riemann y la relatividad general . ^{[ ¿ Investigación original? ]}

El objeto matemático esencial es el de una superficie regular. Aunque las convenciones varían en su definición precisa, estas forman una clase general de subconjuntos del espacio euclidiano tridimensional ( ℝ ³ ) que capturan parte de la noción familiar de "superficie". Al analizar la clase de curvas que se encuentran en dicha superficie y el grado en que las superficies las obligan a curvarse en ℝ ³ , se pueden asociar a cada punto de la superficie dos números, llamados curvaturas principales. Su promedio se llama curvatura media de la superficie y su producto se llama curvatura gaussiana.

Hay muchos ejemplos clásicos de superficies regulares, entre ellos:

• Ejemplos familiares como planos, cilindros y esferas.
• Las superficies mínimas , que se definen por la propiedad de que su curvatura media es cero en cada punto. Los ejemplos más conocidos son los catenoides y los helicoides , aunque se han descubierto muchos más. Las superficies mínimas también se pueden definir por propiedades relacionadas con el área de la superficie , con la consecuencia de que proporcionan un modelo matemático para la forma de las películas de jabón cuando se estiran a lo largo de un marco de alambre.
• superficies regladas , que son superficies que tienen al menos una línea recta que pasa por cada punto; ejemplos incluyen el cilindro y el hiperboloide de una lámina.

Un resultado sorprendente de Carl Friedrich Gauss , conocido como el teorema egregium , mostró que la curvatura gaussiana de una superficie, que por definición tiene que ver con cómo las curvas de la superficie cambian de dirección en el espacio tridimensional, en realidad se puede medir por las longitudes de las curvas que se encuentran en las superficies junto con los ángulos que se forman cuando dos curvas en la superficie se cruzan. Terminológicamente, esto dice que la curvatura gaussiana se puede calcular a partir de la primera forma fundamental (también llamada tensor métrico ) de la superficie. La segunda forma fundamental , por el contrario, es un objeto que codifica cómo se distorsionan las longitudes y los ángulos de las curvas en la superficie cuando las curvas se empujan fuera de la superficie.

A pesar de medir diferentes aspectos de la longitud y el ángulo, la primera y la segunda forma fundamental no son independientes entre sí y satisfacen ciertas restricciones llamadas ecuaciones de Gauss-Codazzi . Un teorema importante, a menudo llamado teorema fundamental de la geometría diferencial de superficies, afirma que siempre que dos objetos satisfacen las restricciones de Gauss-Codazzi, surgirán como la primera y la segunda forma fundamental de una superficie regular.

Utilizando la primera forma fundamental, es posible definir nuevos objetos en una superficie regular. Las geodésicas son curvas en la superficie que satisfacen una cierta ecuación diferencial ordinaria de segundo orden que se especifica mediante la primera forma fundamental. Están muy directamente relacionadas con el estudio de las longitudes de las curvas; una geodésica de longitud suficientemente corta siempre será la curva de menor longitud en la superficie que conecta sus dos puntos finales. Por lo tanto, las geodésicas son fundamentales para el problema de optimización de determinar el camino más corto entre dos puntos dados en una superficie regular.

También se puede definir el transporte paralelo a lo largo de cualquier curva dada, lo que proporciona una prescripción sobre cómo deformar un vector tangente a la superficie en un punto de la curva a vectores tangentes en todos los demás puntos de la curva. La prescripción está determinada por una ecuación diferencial ordinaria de primer orden que se especifica mediante la primera forma fundamental.

Los conceptos anteriores tienen que ver esencialmente con el cálculo multivariable. El teorema de Gauss-Bonnet es un resultado más global, que relaciona la curvatura gaussiana de una superficie con su tipo topológico. Afirma que el valor medio de la curvatura gaussiana está completamente determinado por la característica de Euler de la superficie junto con su área superficial.

Cualquier superficie regular es un ejemplo tanto de una variedad de Riemann como de una superficie de Riemann . Esencialmente, toda la teoría de superficies regulares que se analiza aquí tiene una generalización en la teoría de las variedades de Riemann y sus subvariedades.

Superficies regulares en el espacio euclidiano

Definición

Es intuitivamente claro que una esfera es lisa, mientras que un cono o una pirámide, debido a su vértice o aristas, no lo son. La noción de una "superficie regular" es una formalización de la noción de una superficie lisa. La definición utiliza la representación local de una superficie a través de aplicaciones entre espacios euclidianos . Existe una noción estándar de suavidad para tales aplicaciones; una aplicación entre dos subconjuntos abiertos del espacio euclidiano es lisa si sus derivadas parciales de cada orden existen en cada punto del dominio. ^{[6] [7] [8]}

A continuación se ofrecen tres formas equivalentes de presentar la definición; la definición del medio es quizás la más intuitiva visualmente, ya que esencialmente dice que una superficie regular es un subconjunto de ℝ ³ que es localmente el gráfico de una función suave (ya sea sobre una región en el plano yz , el plano xz o el plano xy ).

Una parametrización local de la forma del parche de Monge para el hemisferio superior de la 2-esfera, obtenida al proyectar sobre el plano xy

Los homeomorfismos que aparecen en la primera definición se conocen como parametrizaciones locales o sistemas de coordenadas locales o cartas locales en S . ^[13] La equivalencia de las dos primeras definiciones afirma que, alrededor de cualquier punto de una superficie regular, siempre existen parametrizaciones locales de la forma ( u , v ) ↦ ( h ( u , v ), u , v ) , ( u , v ) ↦ ( u , h ( u , v ), v ) o ( u , v ) ↦ ( u , v , h ( u , v )) , conocidas como parches de MongeLas funciones F, como en la tercera definición, se denominan funciones definitorias locales . La equivalencia de las tres definiciones se desprende del teorema de la función implícita . ^{[14] [15] [16]}

Los cambios de coordenadas entre diferentes gráficos locales deben ser suaves

Dadas dos parametrizaciones locales cualesquiera f  : V → U y f ′ : V ′→ U ′ de una superficie regular, la composición f ⁻¹ ∘ f ′ es necesariamente suave como una función entre subconjuntos abiertos de ℝ ² . ^[17] Esto muestra que cualquier superficie regular tiene naturalmente la estructura de una variedad suave , con un atlas suave dado por las inversas de las parametrizaciones locales.

En la teoría clásica de la geometría diferencial, las superficies se estudian habitualmente sólo en el caso regular. ^{[7] [18]} Sin embargo, también es común estudiar superficies no regulares, en las que las dos derivadas parciales ∂ _u f y ∂ _v f de una parametrización local pueden no ser linealmente independientes . En este caso, S puede tener singularidades como aristas cuspidales . Estas superficies se estudian típicamente en la teoría de singularidades . Otras formas debilitadas de superficies regulares se dan en el diseño asistido por ordenador , donde una superficie se divide en piezas disjuntas, y las derivadas de las parametrizaciones locales no logran ni siquiera ser continuas a lo largo de los límites. ^{[ cita requerida ]}

Un hiperboloide de dos láminas.

Un toro

Un helicoide

Ejemplos sencillos. Un ejemplo sencillo de superficie regular lo da la 2-esfera {( x , y , z ) | x ² + y ² + z ² = 1 }; esta superficie puede cubrirse con seis parches de Monge (dos de cada uno de los tres tipos dados anteriormente), tomando h ( u , v ) = ± (1 − u ² − v ² ) ^1/2 . También puede cubrirse con dos parametrizaciones locales, utilizando la proyección estereográfica . El conjunto {( x , y , z ) : (( x ² + y ² ) ^1/2 − r ) ² + z ² = R ² } es un toro de revolución con radios r y R . Es una superficie regular; se pueden dar parametrizaciones locales de la forma

${\displaystyle f(s,t)={\big (}(R\cos s+r)\cos t,(R\cos s+r)\sin t,R\sin s{\big )}.}$

El hiperboloide en dos láminas {( x , y , z ): z ² = 1 + x ² + y ² } es una superficie regular; puede ser cubierta por dos parches de Monge, con h ( u , v ) = ±(1 + u ² + v ² ) ^1/2 . El helicoide aparece en la teoría de superficies mínimas . Está cubierto por una única parametrización local, f ( u , v ) = ( u sen v , u cos v , v ) .

Vectores tangentes y vectores normales

Sea S una superficie regular en ℝ ³ , y sea p un elemento de S . Utilizando cualquiera de las definiciones anteriores, se pueden distinguir ciertos vectores en ℝ ³ como tangentes a S en p , y ciertos vectores en ℝ ³ como ortogonales a S en p .

Se ve que el espacio tangente o plano tangente a S en p , que se define como formado por todos los vectores tangentes a S en p , es un subespacio lineal bidimensional de ℝ ³ ; a menudo se denota por T _p S . El espacio normal a S en p , que se define como formado por todos los vectores normales a S en p , es un subespacio lineal unidimensional de ℝ ³ que es ortogonal al espacio tangente T _p S . Como tal, en cada punto p de S , hay dos vectores normales de longitud unitaria (vectores normales unitarios). Los vectores normales unitarios en p se pueden dar en términos de parametrizaciones locales, parches de Monge o funciones de definición locales, a través de las fórmulas

${\displaystyle \pm \left.{\frac {{\frac {\partial f}{\partial u}}\times {\frac {\partial f}{\partial v}}}{{\big \|}{\frac {\partial f}{\partial u}}\times {\frac {\partial f}{\partial v}}{\big \|}}}\right|_{f^{-1}(p)},\qquad \pm \left.{\frac {{\big (}{\frac {\partial h}{\partial u}},{\frac {\partial h}{\partial v}},-1{\big )}}{\sqrt {1+{\big (}{\frac {\partial h}{\partial u}}{\big )}^{2}+{\big (}{\frac {\partial h}{\partial v}}{\big )}^{2}}}}\right|_{(p_{1},p_{2})},\qquad {\text{or}}\qquad \pm {\frac {\nabla F(p)}{{\big \|}\nabla F(p){\big \|}}},}$

siguiendo las mismas notaciones que en las definiciones anteriores.

También es útil observar una definición "intrínseca" de vectores tangentes, que es típica de la generalización de la teoría de superficies regulares al contexto de variedades suaves . Define el espacio tangente como un espacio vectorial real bidimensional abstracto, en lugar de como un subespacio lineal de ℝ ³ . En esta definición, se dice que un vector tangente a S en p es una asignación, a cada parametrización local f  : V → S con p ∈ f ( V ) , de dos números X ¹ y X ² , tal que para cualquier otra parametrización local f ′ : V → S con p ∈ f ( V ) (y con los números correspondientes ( X ′) ¹ y ( X ′) ² ), se tiene

${\displaystyle {\begin{pmatrix}X^{1}\\X^{2}\end{pmatrix}}=A_{f'(p)}{\begin{pmatrix}(X')^{1}\\(X')^{2}\end{pmatrix}},}$

donde A _{f ′( p )} es la matriz jacobiana de la función f ⁻¹ ∘ f ′ , evaluada en el punto f ′( p ) . La colección de vectores tangentes a S en p tiene naturalmente la estructura de un espacio vectorial bidimensional. Un vector tangente en este sentido corresponde a un vector tangente en el sentido anterior considerando el vector

${\displaystyle X^{1}{\frac {\partial f}{\partial u}}+X^{2}{\frac {\partial f}{\partial v}}.}$

en ℝ ³ . La condición jacobiana en X ¹ y X ² asegura, por la regla de la cadena , que este vector no depende de f .

Para funciones suaves sobre una superficie, los campos vectoriales (es decir, los campos vectoriales tangentes) tienen una interpretación importante como operadores o derivaciones de primer orden. Sea una superficie regular, un subconjunto abierto del plano y un gráfico de coordenadas. Si , el espacio se puede identificar con . De manera similar, identifica campos vectoriales en con campos vectoriales en . Tomando las variables estándar u y v , un campo vectorial tiene la forma , con a y b funciones suaves. Si es un campo vectorial y es una función suave, entonces es también una función suave. El operador diferencial de primer orden es una derivación , es decir, satisface la regla de Leibniz ^[19] ${\displaystyle S}$ ${\displaystyle U}$ ${\displaystyle f:U\rightarrow S}$ ${\displaystyle V=f(U)}$ ${\displaystyle C^{\infty }(U)}$ ${\displaystyle C^{\infty }(V)}$ ${\displaystyle f}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle X=a\partial _{u}+b\partial _{v}}$ ${\displaystyle X}$ ${\displaystyle g}$ ${\displaystyle Xg}$ ${\displaystyle X}$ ${\displaystyle X(gh)=(Xg)h+g(Xh).}$

Para los campos vectoriales X e Y es sencillo comprobar que el operador es una derivación correspondiente a un campo vectorial. Se denomina corchete de Lie . Es antisimétrico y satisface la identidad de Jacobi: ${\displaystyle [X,Y]=XY-YX}$ ${\displaystyle [X,Y]}$ ${\displaystyle [X,Y]=-[Y,X]}$

${\displaystyle [[X,Y],Z]+[[Y,Z],X]+[[Z,X],Y]=0.}$

En resumen, los campos vectoriales forman un álgebra de Lie bajo el corchete de Lie. ^[20] ${\displaystyle U}$ ${\displaystyle V}$

Primera y segunda formas fundamentales, el operador de forma y la curvatura

Sea S una superficie regular en ℝ ³ . Dada una parametrización local f  : V → S y un campo vectorial normal unitario n a f ( V ) , se definen los siguientes objetos como funciones de valor real o de valor matricial en V . La primera forma fundamental depende sólo de f , y no de n . La cuarta columna registra la forma en que estas funciones dependen de f , relacionando las funciones E ′, F ′, G ′, L ′, etc., que surgen para una elección diferente de parametrización local, f ′ : V ′ → S , con las que surgen para f . Aquí A denota la matriz jacobiana de f ^–1 ∘ f ′ . La relación clave para establecer las fórmulas de la cuarta columna es entonces

${\displaystyle {\begin{pmatrix}{\frac {\partial f'}{\partial u}}\\{\frac {\partial f'}{\partial v}}\end{pmatrix}}=A{\begin{pmatrix}{\frac {\partial f}{\partial u}}\\{\frac {\partial f}{\partial v}}\end{pmatrix}},}$

como sigue por la regla de la cadena .

Mediante un cálculo directo con la matriz que define el operador de forma, se puede comprobar que la curvatura gaussiana es el determinante del operador de forma, la curvatura media es la mitad de la traza del operador de forma y las curvaturas principales son los valores propios del operador de forma; además, la curvatura gaussiana es el producto de las curvaturas principales y la curvatura media es su suma. Estas observaciones también se pueden formular como definiciones de estos objetos. Estas observaciones también dejan claro que las últimas tres filas de la cuarta columna se derivan inmediatamente de la fila anterior, ya que matrices similares tienen determinante, traza y valores propios idénticos. Es fundamental observar que E , G y EG − F ² son necesariamente positivos. Esto garantiza que la matriz inversa en la definición del operador de forma esté bien definida y que las curvaturas principales sean números reales.

Obsérvese también que una negación de la elección del campo vectorial normal unitario negará la segunda forma fundamental, el operador de forma, la curvatura media y las curvaturas principales, pero dejará la curvatura gaussiana sin cambios. En resumen, esto ha demostrado que, dada una superficie regular S , la curvatura gaussiana de S puede considerarse como una función de valor real en S ; en relación con una elección del campo vectorial normal unitario en todos los S , las dos curvaturas principales y la curvatura media también son funciones de valor real en S .

Definición de segunda forma fundamental

Las curvaturas principales en un punto de una superficie

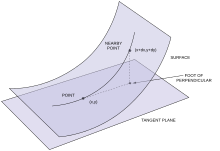
Geométricamente, la primera y la segunda forma fundamental pueden considerarse como una fuente de información sobre cómo f ( u , v ) se mueve en ℝ ³ a medida que ( u , v ) se mueve en V . En particular, la primera forma fundamental codifica la rapidez con la que se mueve f , mientras que la segunda forma fundamental codifica hasta qué punto su movimiento se produce en la dirección del vector normal n . En otras palabras, la segunda forma fundamental en un punto p codifica la longitud de la proyección ortogonal desde S al plano tangente a S en p ; en particular, proporciona la función cuadrática que mejor se aproxima a esta longitud. Este razonamiento se puede precisar mediante las fórmulas

${\displaystyle {\begin{aligned}\lim _{(h,k)\to (0,0)}{\frac {{\big |}f(u+h,v+k)-f(u,v){\big |}^{2}-{\big (}Eh^{2}+2Fhk+Gk^{2}{\big )}}{h^{2}+k^{2}}}&=0\\\lim _{(h,k)\to (0,0)}{\frac {{\big (}f(u+h,v+k)-f(u,v){\big )}\cdot n-{\frac {1}{2}}{\big (}Lh^{2}+2Mhk+Nk^{2}{\big )}}{h^{2}+k^{2}}}&=0,\end{aligned}}}$

como se desprende directamente de las definiciones de las formas fundamentales y del teorema de Taylor en dos dimensiones. Las curvaturas principales pueden verse de la siguiente manera. En un punto dado p de S , considérese el conjunto de todos los planos que contienen la línea ortogonal a S . Cada uno de estos planos tiene una curva de intersección con S , que puede considerarse como una curva plana dentro del propio plano. Las dos curvaturas principales en p son los valores máximo y mínimo posibles de la curvatura de esta curva plana en p , a medida que el plano en consideración gira alrededor de la línea normal.

A continuación se resume el cálculo de las cantidades anteriores en relación con un parche de Monge f ( u , v ) = ( u , v , h ( u , v )) . Aquí h _u y h _v denotan las dos derivadas parciales de h , con notación análoga para las segundas derivadas parciales. La segunda forma fundamental y todas las cantidades posteriores se calculan en relación con la elección dada del campo vectorial normal unitario.

Símbolos de Christoffel, ecuaciones de Gauss-Codazzi y el teorema Egregium

Sea S una superficie regular en ℝ ³ . Los símbolos de Christoffel asignan, a cada parametrización local f  : V → S , ocho funciones sobre V , definidas por ^[22]

${\displaystyle {\begin{pmatrix}\Gamma _{11}^{1}&\Gamma _{12}^{1}&\Gamma _{21}^{1}&\Gamma _{22}^{1}\\\Gamma _{11}^{2}&\Gamma _{12}^{2}&\Gamma _{21}^{2}&\Gamma _{22}^{2}\end{pmatrix}}={\begin{pmatrix}E&F\\F&G\end{pmatrix}}^{-1}{\begin{pmatrix}{\frac {1}{2}}{\frac {\partial E}{\partial u}}&{\frac {1}{2}}{\frac {\partial E}{\partial v}}&{\frac {1}{2}}{\frac {\partial E}{\partial v}}&{\frac {\partial F}{\partial v}}-{\frac {1}{2}}{\frac {\partial G}{\partial u}}\\{\frac {\partial F}{\partial u}}-{\frac {1}{2}}{\frac {\partial E}{\partial v}}&{\frac {1}{2}}{\frac {\partial G}{\partial u}}&{\frac {1}{2}}{\frac {\partial G}{\partial u}}&{\frac {1}{2}}{\frac {\partial G}{\partial v}}\end{pmatrix}}.}$

También se pueden definir mediante las siguientes fórmulas, en las que n es un campo vectorial normal unitario a lo largo de f ( V ) y L , M , N son los componentes correspondientes de la segunda forma fundamental:

${\displaystyle {\begin{aligned}{\frac {\partial ^{2}f}{\partial u^{2}}}&=\Gamma _{11}^{1}{\frac {\partial f}{\partial u}}+\Gamma _{11}^{2}{\frac {\partial f}{\partial v}}+Ln\\{\frac {\partial ^{2}f}{\partial u\partial v}}&=\Gamma _{12}^{1}{\frac {\partial f}{\partial u}}+\Gamma _{12}^{2}{\frac {\partial f}{\partial v}}+Mn\\{\frac {\partial ^{2}f}{\partial v^{2}}}&=\Gamma _{22}^{1}{\frac {\partial f}{\partial u}}+\Gamma _{22}^{2}{\frac {\partial f}{\partial v}}+Nn.\end{aligned}}}$

La clave de esta definición es que ⁠∂f​/∂ tu⁠ , ⁠∂f​/∂ en⁠ , y n forman una base de ℝ ³ en cada punto, en relación con la cual cada una de las tres ecuaciones especifica de manera única los símbolos de Christoffel como coordenadas de las segundas derivadas parciales de f . La elección de la normal unitaria no tiene efecto sobre los símbolos de Christoffel, ya que si n se intercambia por su negación, entonces los componentes de la segunda forma fundamental también se niegan, y por lo tanto los signos de Ln , Mn , Nn no cambian.

La segunda definición muestra, en el contexto de parametrizaciones locales, que los símbolos de Christoffel son geométricamente naturales. Aunque las fórmulas de la primera definición parecen menos naturales, tienen la importancia de mostrar que los símbolos de Christoffel pueden calcularse a partir de la primera forma fundamental, lo que no resulta inmediatamente evidente a partir de la segunda definición. La equivalencia de las definiciones puede comprobarse sustituyendo directamente la primera definición en la segunda y utilizando las definiciones de E , F , G .

Las ecuaciones de Codazzi afirman que ^[23]

${\displaystyle {\begin{aligned}{\frac {\partial L}{\partial v}}-{\frac {\partial M}{\partial u}}&=L\Gamma _{12}^{1}+M(\Gamma _{12}^{2}-\Gamma _{11}^{1})-N\Gamma _{11}^{2}\\{\frac {\partial M}{\partial v}}-{\frac {\partial N}{\partial u}}&=L\Gamma _{22}^{1}+M(\Gamma _{22}^{2}-\Gamma _{12}^{1})-N\Gamma _{12}^{2}.\end{aligned}}}$

Estas ecuaciones se pueden derivar directamente de la segunda definición de los símbolos de Christoffel dada anteriormente; por ejemplo, la primera ecuación de Codazzi se obtiene diferenciando la primera ecuación con respecto a v , la segunda ecuación con respecto a u , restando las dos y tomando el producto escalar con n . La ecuación de Gauss afirma que ^[24]

${\displaystyle {\begin{aligned}KE&={\frac {\partial \Gamma _{11}^{2}}{\partial v}}-{\frac {\partial \Gamma _{21}^{2}}{\partial u}}+\Gamma _{21}^{2}\Gamma _{11}^{1}+\Gamma _{22}^{2}\Gamma _{11}^{2}-\Gamma _{11}^{2}\Gamma _{21}^{1}-\Gamma _{12}^{2}\Gamma _{21}^{2}\\KF&={\frac {\partial \Gamma _{12}^{2}}{\partial v}}-{\frac {\partial \Gamma _{22}^{2}}{\partial u}}+\Gamma _{21}^{2}\Gamma _{12}^{1}-\Gamma _{11}^{2}\Gamma _{22}^{1}\\KG&={\frac {\partial \Gamma _{22}^{1}}{\partial u}}-{\frac {\partial \Gamma _{12}^{1}}{\partial v}}+\Gamma _{11}^{1}\Gamma _{22}^{1}+\Gamma _{12}^{1}\Gamma _{22}^{2}-\Gamma _{21}^{1}\Gamma _{12}^{1}-\Gamma _{22}^{1}\Gamma _{12}^{2}\end{aligned}}}$

Estas se pueden derivar de manera similar a las ecuaciones de Codazzi, con una de ellas utilizando las ecuaciones de Weingarten en lugar de tomar el producto escalar con n . Aunque estas se escriben como tres ecuaciones separadas, son idénticas cuando se sustituyen las definiciones de los símbolos de Christoffel, en términos de la primera forma fundamental. Hay muchas maneras de escribir la expresión resultante, una de ellas derivada en 1852 por Brioschi utilizando un hábil uso de determinantes: ^{[25] [26]}

${\displaystyle K={\frac {1}{(EG-F^{2})^{2}}}\det {\begin{pmatrix}-{1 \over 2}{\frac {\partial ^{2}E}{\partial v^{2}}}+{\frac {\partial ^{2}F}{\partial u\partial v}}-{1 \over 2}{\frac {\partial ^{2}G}{\partial u^{2}}}&{1 \over 2}{\frac {\partial E}{\partial u}}&{\frac {\partial F}{\partial u}}-{1 \over 2}{\frac {\partial E}{\partial v}}\\{\frac {\partial F}{\partial v}}-{1 \over 2}{\frac {\partial G}{\partial u}}&E&F\\{1 \over 2}{\frac {\partial G}{\partial v}}&F&G\end{pmatrix}}-{\frac {1}{(EG-F^{2})^{2}}}\det {\begin{pmatrix}0&{1 \over 2}{\frac {\partial E}{\partial v}}&{1 \over 2}{\frac {\partial G}{\partial u}}\\{1 \over 2}{\frac {\partial E}{\partial v}}&E&F\\{1 \over 2}{\frac {\partial G}{\partial u}}&F&G\end{pmatrix}}.}$

Cuando se considera que los símbolos de Christoffel están definidos por la primera forma fundamental, las ecuaciones de Gauss y Codazzi representan ciertas restricciones entre la primera y la segunda forma fundamental. La ecuación de Gauss es particularmente notable, ya que muestra que la curvatura gaussiana se puede calcular directamente a partir de la primera forma fundamental, sin necesidad de ninguna otra información; equivalentemente, esto dice que LN − M ² puede escribirse en realidad como una función de E , F , G , aunque los componentes individuales L , M , N no puedan. Esto se conoce como el teorema egregium , y fue un descubrimiento importante de Carl Friedrich Gauss . Es particularmente sorprendente cuando uno recuerda la definición geométrica de la curvatura gaussiana de S como definida por los radios máximo y mínimo de los círculos osculadores; parecen estar definidos fundamentalmente por la geometría de cómo S se dobla dentro de ℝ ³ . Sin embargo, el teorema muestra que su producto puede determinarse a partir de la geometría "intrínseca" de S , que sólo tiene que ver con las longitudes de las curvas a lo largo de S y los ángulos formados en sus intersecciones. Como dijo Marcel Berger : ^[27]

Este teorema es desconcertante. [...] Es el tipo de teorema que podría haber esperado decenas de años más antes de ser descubierto por otro matemático ya que, a diferencia de gran parte de la historia intelectual, no estaba en absoluto en el aire. [...] Hasta donde sabemos, no existe hoy una prueba geométrica sencilla del teorema egregium.

Las ecuaciones de Gauss-Codazzi también pueden expresarse sucintamente y derivarse en el lenguaje de las formas de conexión debido a Élie Cartan . ^[28] En el lenguaje del cálculo tensorial , haciendo uso de métricas naturales y conexiones en fibrados tensoriales , la ecuación de Gauss puede escribirse como H ² − | h | ² = R y las dos ecuaciones de Codazzi pueden escribirse como ∇ ₁ h ₁₂ = ∇ ₂ h ₁₁ y ∇ ₁ h ₂₂ = ∇ ₂ h ₁₂ ; las expresiones complicadas que tienen que ver con los símbolos de Christoffel y la primera forma fundamental se absorben completamente en las definiciones de la derivada tensorial covariante ∇ h y la curvatura escalar R . Pierre Bonnet demostró que dos formas cuadráticas que satisfacen las ecuaciones de Gauss-Codazzi siempre determinan de forma única una superficie incrustada localmente. ^[29] Por esta razón, las ecuaciones de Gauss-Codazzi se denominan a menudo ecuaciones fundamentales para superficies embebidas, identificando con precisión de dónde provienen las curvaturas intrínsecas y extrínsecas. Admiten generalizaciones a superficies embebidas en variedades riemannianas más generales .

Isometrías

Se dice que un difeomorfismo entre conjuntos abiertos y en una superficie regular es una isometría si conserva la métrica, es decir, la primera forma fundamental. ^{[30] [31] [32]} Por lo tanto, para cada punto en y vectores tangentes en , existen igualdades ${\displaystyle \varphi }$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle S}$ ${\displaystyle p}$ ${\displaystyle U}$ ${\displaystyle w_{1},\,\,w_{2}}$ ${\displaystyle p}$

${\displaystyle E(p)w_{1}\cdot w_{1}+2F(p)w_{1}\cdot w_{2}+G(p)w_{2}\cdot w_{2}=E(\varphi (p))\varphi ^{\prime }(w_{1})\cdot \varphi ^{\prime }(w_{1})+2F(\varphi (p))\varphi ^{\prime }(w_{1})\cdot \varphi ^{\prime }(w_{2})+G(\varphi (p))\varphi ^{\prime }(w_{1})\cdot \varphi ^{\prime }(w_{2}).}$

En términos del producto interno que proviene de la primera forma fundamental, esto se puede reescribir como

${\displaystyle (w_{1},w_{2})_{p}=(\varphi ^{\prime }(w_{1}),\varphi ^{\prime }(w_{2}))_{\varphi (p)}}$.

El catenoide es una superficie regular de revolución.

Por otra parte, la longitud de una curva parametrizada se puede calcular como ${\displaystyle \gamma (t)=(x(t),y(t))}$

${\displaystyle L(\gamma )=\int _{a}^{b}{\sqrt {E{\dot {x}}\cdot {\dot {x}}+2F{\dot {x}}\cdot {\dot {y}}+G{\dot {y}}\cdot {\dot {y}}}}\,dt}$

y, si la curva se encuentra en , las reglas para el cambio de variables muestran que ${\displaystyle U}$

${\displaystyle L(\varphi \circ \gamma )=L(\gamma ).}$

Por el contrario, si conserva las longitudes de todos los parametrizados en curvas, entonces es una isometría. De hecho, para elecciones adecuadas de , los vectores tangentes y dan vectores tangentes arbitrarios y . Las igualdades deben cumplirse para todas las elecciones de vectores tangentes y así como y , de modo que . ^[33] ${\displaystyle \varphi }$ ${\displaystyle \varphi }$ ${\displaystyle \gamma }$ ${\displaystyle {\dot {x}}}$ ${\displaystyle {\dot {y}}}$ ${\displaystyle w_{1}}$ ${\displaystyle w_{2}}$ ${\displaystyle w_{1}}$ ${\displaystyle w_{2}}$ ${\displaystyle \varphi ^{\prime }(w_{1})}$ ${\displaystyle \varphi ^{\prime }(w_{2})}$ ${\displaystyle (\varphi ^{\prime }(w_{1}),\varphi ^{\prime }(w_{2}))_{\varphi (p)}=(w_{1},w_{1})_{p}}$

Un ejemplo simple de isometría lo proporcionan dos parametrizaciones y de un conjunto abierto en superficies regulares y . Si , y , entonces es una isometría de sobre . ^[34] ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$ ${\displaystyle U}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle E_{1}=E_{2}}$ ${\displaystyle F_{1}=F_{2}}$ ${\displaystyle G_{1}=G_{2}}$ ${\displaystyle \varphi =f_{2}\circ f_{1}^{-1}}$ ${\displaystyle f_{1}(U)}$ ${\displaystyle f_{2}(U)}$

El cilindro y el plano dan ejemplos de superficies que son localmente isométricas pero que no pueden extenderse a una isometría por razones topológicas. ^[35] Como otro ejemplo, el catenoide y el helicoide son localmente isométricos. ^[36]

Derivadas covariantes

Un campo vectorial tangente X sobre S asigna, a cada p en S , un vector tangente X _p a S en p . Según la definición "intrínseca" de vectores tangentes dada anteriormente, un campo vectorial tangente X asigna entonces, a cada parametrización local f  : V → S , dos funciones reales X ¹ y X ² sobre V , de modo que

${\displaystyle X_{p}=X^{1}{\big (}f^{-1}(p){\big )}{\frac {\partial f}{\partial u}}{\Big |}_{f^{-1}(p)}+X^{2}{\big (}f^{-1}(p){\big )}{\frac {\partial f}{\partial v}}{\Big |}_{f^{-1}(p)}}$

para cada p en S . Se dice que X es suave si las funciones X ¹ y X ² son suaves, para cualquier elección de f . ^[37] De acuerdo con las otras definiciones de vectores tangentes dadas anteriormente, también se puede considerar un campo vectorial tangencial X en S como una función X  : S → ℝ ³ tal que X ( p ) está contenido en el espacio tangente T _p S ⊂ ℝ ³ para cada p en S . Como es común en la situación más general de variedades suaves , los campos vectoriales tangenciales también se pueden definir como ciertos operadores diferenciales en el espacio de funciones suaves en S .

Las derivadas covariantes (también llamadas "derivadas tangenciales") de Tullio Levi-Civita y Gregorio Ricci-Curbastro proporcionan un medio para diferenciar campos vectoriales tangenciales suaves. Dado un campo vectorial tangencial X y un vector tangente Y a S en p , la derivada covariante ∇ _Y X es un cierto vector tangente a S en p . En consecuencia, si X e Y son ambos campos vectoriales tangenciales, entonces ∇ _Y X también puede considerarse como un campo vectorial tangencial; iterativamente, si X , Y y Z son campos vectoriales tangenciales, se puede calcular ∇ _Z ∇ _Y X , que será otro campo vectorial tangencial. Hay algunas formas de definir la derivada covariante; la primera a continuación utiliza los símbolos de Christoffel y la definición "intrínseca" de vectores tangentes, y la segunda es más manifiestamente geométrica.

Dado un campo vectorial tangente X y un vector tangente Y a S en p , se define ∇ _Y X como el vector tangente a p que asigna a una parametrización local f  : V → S los dos números

${\displaystyle (\nabla _{Y}X)^{k}=D_{(Y^{1},Y^{2})}X^{k}{\Big |}_{f^{-1}(p)}+\sum _{i=1}^{2}\sum _{j=1}^{2}{\big (}\Gamma _{ij}^{k}X^{j}{\big )}{\Big |}_{f^{-1}(p)}Y^{i},\qquad (k=1,2)}$

donde D _{( Y ¹ , Y ² )} es la derivada direccional . ^[38] Esto a menudo se abrevia en la forma menos engorrosa (∇ _Y X ) ^k = ∂ _Y ( X ^k ) + Y ⁱ Γ ^yo
_ijX ^j , haciendo uso de la notación de Einstein y con las ubicaciones de la evaluación de la función entendidas implícitamente. Esto sigue una prescripción estándar en geometría de Riemann para obtener una conexión a partir de una métrica de Riemann . Es un hecho fundamental que el vector

${\displaystyle (\nabla _{Y}X)^{1}{\frac {\partial f}{\partial u}}+(\nabla _{Y}X)^{2}{\frac {\partial f}{\partial v}}}$

en ℝ ³ es independiente de la elección de la parametización local f , aunque esto es bastante tedioso de comprobar.

También se puede definir la derivada covariante mediante el siguiente enfoque geométrico, que no hace uso de símbolos de Christoffel o parametrizaciones locales. ^{[39] [40] [41]} Sea X un campo vectorial en S , visto como una función S → ℝ ³ . Dada cualquier curva c  : ( a , b ) → S , se puede considerar la composición X ∘ c  : ( a , b ) → ℝ ³ . Como una función entre espacios euclidianos, se puede diferenciar en cualquier valor de entrada para obtener un elemento ( X ∘ c )′( t ) de ℝ ³ . La proyección ortogonal de este vector sobre T _{c ( t )} S define la derivada covariante ∇ _{c ′( t )} X . Aunque ésta es una definición geométricamente muy limpia, es necesario demostrar que el resultado sólo depende de c ′( t ) y X , y no de c y X ; se pueden utilizar parametrizaciones locales para este pequeño argumento técnico.

No es inmediatamente evidente a partir de la segunda definición que la diferenciación covariante depende solo de la primera forma fundamental de S ; sin embargo, esto es inmediato a partir de la primera definición, ya que los símbolos de Christoffel se pueden definir directamente a partir de la primera forma fundamental. Es sencillo comprobar que las dos definiciones son equivalentes. La clave es que cuando se considera X ¹ ⁠∂f​/∂ tu+ X ²​​∂f​/∂ en⁠ como una función ℝ ³ -valuada, su diferenciación a lo largo de una curva da como resultado segundas derivadas parciales ∂ ² f ; los símbolos de Christoffel entran con proyección ortogonal al espacio tangente, debido a la formulación de los símbolos de Christoffel como los componentes tangenciales de las segundas derivadas de f relativas a la base ⁠∂f​/∂ tu⁠ , ⁠∂f​/∂ en⁠ , n . ^[38] Esto se analiza en la sección anterior.

El lado derecho de las tres ecuaciones de Gauss se puede expresar mediante la diferenciación covariante. Por ejemplo, el lado derecho

${\displaystyle {\frac {\partial \Gamma _{11}^{2}}{\partial v}}-{\frac {\partial \Gamma _{21}^{2}}{\partial u}}+\Gamma _{21}^{2}\Gamma _{11}^{1}+\Gamma _{22}^{2}\Gamma _{11}^{2}-\Gamma _{11}^{2}\Gamma _{21}^{1}-\Gamma _{12}^{2}\Gamma _{21}^{2}}$

puede reconocerse como la segunda coordenada de

${\displaystyle \nabla _{\frac {\partial f}{\partial v}}\nabla _{\frac {\partial f}{\partial u}}{\frac {\partial f}{\partial u}}-\nabla _{\frac {\partial f}{\partial u}}\nabla _{\frac {\partial f}{\partial v}}{\frac {\partial f}{\partial u}}}$

relativo a la base∂f​/∂ tu⁠ , ⁠∂f​/∂ en⁠ , como se puede verificar directamente utilizando la definición de diferenciación covariante por símbolos de Christoffel. En el lenguaje de la geometría de Riemann , esta observación también se puede expresar diciendo que los lados derechos de las ecuaciones de Gauss son varios componentes de la curvatura de Ricci de la conexión de Levi-Civita de la primera forma fundamental, cuando se interpreta como una métrica de Riemann .

Ejemplos

Superficie de revolución obtenida al rotar la curva x = 2 + cos z alrededor del eje z .

Superficies de revolución

Una superficie de revolución se obtiene rotando una curva en el plano xz alrededor del eje z . Tales superficies incluyen esferas, cilindros, conos, toros y la catenoide . Los elipsoides , hiperboloides y paraboloides generales no lo son. Supongamos que la curva está parametrizada por

${\displaystyle x=c_{1}(s),\,\,z=c_{2}(s)}$

con s extraída de un intervalo ( a , b ) . Si c ₁ nunca es cero, si c ₁ ′ y c ₂ ′ nunca son ambos iguales a cero, y si c ₁ y c ₂ son ambos lisos, entonces la superficie de revolución correspondiente

${\displaystyle S={\Big \{}{\big (}c_{1}(s)\cos t,c_{1}(s)\sin t,c_{2}(s){\big )}\colon s\in (a,b){\text{ and }}t\in \mathbb {R} {\Big \}}}$

será una superficie regular en ℝ ³ . Una parametrización local f  : ( a , b ) × (0, 2π) → S viene dada por

${\displaystyle f(s,t)={\big (}c_{1}(s)\cos t,c_{1}(s)\sin t,c_{2}(s){\big )}.}$

En relación a esta parametrización, los datos geométricos son: ^[42]

En el caso especial de que la curva original esté parametrizada por la longitud de arco, es decir ( c ₁ ′( s )) ² + ( c ₂ ′( s )) ² = 1 , se puede derivar para encontrar c ₁ ′( s ) c ₁ ′′( s ) + c ₂ ′( s ) c ₂ ′′( s ) = 0 . Al sustituir en la curvatura gaussiana, se tiene la ecuación simplificada

${\displaystyle K=-{\frac {c_{1}''(s)}{c_{1}(s)}}\qquad {\text{and}}\qquad H=c_{1}'(s)c_{2}''(s)-c_{2}'(s)c_{1}''(s)+{\frac {c_{2}'(s)}{c_{1}(s)}}.}$

La simplicidad de esta fórmula hace que sea particularmente fácil estudiar la clase de superficies rotacionalmente simétricas con curvatura gaussiana constante. ^[43] Por reducción al caso alternativo de que c ₂ (s) = s , se pueden estudiar las superficies mínimas rotacionalmente simétricas, con el resultado de que cualquier superficie de este tipo es parte de un plano o un catenoide escalado. ^[44]

Cada curva t constante en S se puede parametrizar como una geodésica; una curva s constante en S se puede parametrizar como una geodésica si y solo si c ₁ ′(s) es igual a cero. En general, las geodésicas en S se rigen por la relación de Clairaut .

Un elipsoide cuadrático

Superficies cuadráticas

Consideremos la superficie cuadrática definida por ^[45]

${\displaystyle {x^{2} \over a}+{y^{2} \over b}+{z^{2} \over c}=1.}$

Esta superficie admite una parametrización

${\displaystyle x={\sqrt {a(a-u)(a-v) \over (a-b)(a-c)}},\,\,y={\sqrt {b(b-u)(b-v) \over (b-a)(b-c)}},\,\,z={\sqrt {c(c-u)(c-v) \over (c-b)(c-a)}}.}$

La curvatura gaussiana y la curvatura media se dan por

${\displaystyle K={abc \over u^{2}v^{2}},\,\,K_{m}=-(u+v){\sqrt {abc \over u^{3}v^{3}}}.}$

Un hiperboloide cuadrático de una sola hoja que es una superficie reglada de dos maneras diferentes.

Superficies regladas

Una superficie reglada es aquella que puede generarse mediante el movimiento de una línea recta en E ³ . ^[46] Al elegir una directriz en la superficie, es decir, una curva de velocidad unitaria suave c ( t ) ortogonal a las líneas rectas, y luego elegir u ( t ) como vectores unitarios a lo largo de la curva en la dirección de las líneas, el vector de velocidad v = c _t y u satisfacen

${\displaystyle u\cdot v=0,\,\,\|u\|=1,\,\,\|v\|=1.}$

La superficie está formada por puntos.

${\displaystyle c(t)+s\cdot u(t)}$

a medida que s y t varían.

Entonces, si

${\displaystyle a=\|u_{t}\|,\,\,b=u_{t}\cdot v,\,\,\alpha =-{\frac {b}{a^{2}}},\,\,\beta ={\frac {\sqrt {a^{2}-b^{2}}}{a^{2}}},}$

La curvatura gaussiana y media se dan por

${\displaystyle K=-{\beta ^{2} \over ((s-\alpha )^{2}+\beta ^{2})^{2}},\,\,K_{m}=-{r[(s-\alpha )^{2}+\beta ^{2})]+\beta _{t}(s-\alpha )+\beta \alpha _{t} \over [(s-\alpha )^{2}+\beta ^{2}]^{\frac {3}{2}}}.}$

La curvatura gaussiana de la superficie reglada se desvanece si y solo si u _t y v son proporcionales, ^[47] Esta condición es equivalente a que la superficie sea la envolvente de los planos a lo largo de la curva que contienen al vector tangente v y al vector ortogonal u , es decir, a que la superficie sea desarrollable a lo largo de la curva. ^[48] De manera más general, una superficie en E ³ tiene una curvatura gaussiana que se desvanece cerca de un punto si y solo si es desarrollable cerca de ese punto. ^[49] (A continuación se da una condición equivalente en términos de la métrica).

Superficies mínimas

En 1760, Lagrange amplió los resultados de Euler sobre el cálculo de variaciones que involucraban integrales en una variable a dos variables. ^[50] Tenía en mente el siguiente problema:

Dada una curva cerrada en E ³ , encuentre una superficie que tenga la curva como límite con área mínima.

Una superficie de este tipo se denomina superficie mínima .

En 1776, Jean Baptiste Meusnier demostró que la ecuación diferencial derivada de Lagrange era equivalente a la desaparición de la curvatura media de la superficie:

Una superficie es mínima si y sólo si su curvatura media se desvanece.

Las superficies mínimas tienen una interpretación sencilla en la vida real: son la forma que adoptará una película de jabón si se sumerge un marco de alambre con la forma de la curva en una solución de jabón y luego se saca con cuidado. La cuestión de si existe una superficie mínima con un límite determinado se denomina problema de Plateau en honor al físico belga Joseph Plateau, que realizó experimentos con películas de jabón a mediados del siglo XIX. En 1930, Jesse Douglas y Tibor Radó dieron una respuesta afirmativa al problema de Plateau (Douglas recibió una de las primeras medallas Fields por este trabajo en 1936). ^[51]

Se conocen muchos ejemplos explícitos de superficies mínimas, como la catenoide , la helicoide , la superficie de Scherk y la superficie de Enneper . Se han realizado numerosas investigaciones en esta área, resumidas en Osserman (2002). En particular, un resultado de Osserman muestra que si una superficie mínima no es plana, entonces su imagen bajo el mapa de Gauss es densa en S ² .

Superficies de curvatura gaussiana constante

Eugenio Beltrami (1835-1899)

Si una superficie tiene una curvatura gaussiana constante, se denomina superficie de curvatura constante . ^[52]

• La esfera unitaria en E ³ tiene curvatura gaussiana constante +1.
• Tanto el plano euclidiano como el cilindro tienen una curvatura gaussiana constante 0.
• Una pseudoesfera unitaria tiene una curvatura gaussiana constante -1 (aparte de su ecuador, que es singular ). La pseudoesfera se puede obtener rotando una tractriz alrededor de su asíntota. En 1868 Eugenio Beltrami demostró que la geometría de la pseudoesfera estaba directamente relacionada con la del plano hiperbólico más abstracto , descubierto independientemente por Lobachevsky (1830) y Bolyai (1832). Ya en 1840, F. Minding, un estudiante de Gauss, había obtenido fórmulas trigonométricas para la pseudoesfera idénticas a las del plano hiperbólico. ^[53] La geometría intrínseca de esta superficie se entiende ahora mejor en términos de la métrica de Poincaré en el semiplano superior o el disco unitario , y ha sido descrita por otros modelos como el modelo de Klein o el modelo hiperboloide , obtenido al considerar el hiperboloide de dos láminas q ( x , y , z ) = −1 en el espacio tridimensional de Minkowski , donde q ( x , y , z ) = x ² + y ² – z ² . ^[54]

La esfera, el plano y el plano hiperbólico tienen grupos de simetrías de Lie transitivos . Este hecho teórico de grupos tiene consecuencias de largo alcance, tanto más notables debido al papel central que estas superficies especiales desempeñan en la geometría de superficies, debido al teorema de uniformización de Poincaré (ver más abajo).

Otros ejemplos de superficies con curvatura gaussiana 0 incluyen conos , superficies desarrollables tangentes y, más generalmente, cualquier superficie desarrollable.

Estructura métrica local

Para cualquier superficie incrustada en el espacio euclidiano de dimensión 3 o superior, es posible medir la longitud de una curva en la superficie, el ángulo entre dos curvas y el área de una región en la superficie. Esta estructura se codifica infinitesimalmente en una métrica de Riemann en la superficie a través de elementos de línea y elementos de área . Clásicamente, en los siglos XIX y principios del XX, solo se consideraban superficies incrustadas en R ³ y la métrica se daba como una matriz definida positiva de 2 × 2 que variaba suavemente de un punto a otro en una parametrización local de la superficie. La idea de parametrización local y cambio de coordenadas se formalizó más tarde a través de la noción abstracta actual de una variedad , un espacio topológico donde la estructura suave está dada por cartas locales en la variedad, exactamente como el planeta Tierra está mapeado por atlas hoy. Se requiere que los cambios de coordenadas entre diferentes cartas de la misma región sean suaves. De la misma manera que las curvas de nivel en los mapas de la vida real codifican los cambios de elevación, teniendo en cuenta las distorsiones locales de la superficie de la Tierra para calcular las distancias reales, la métrica de Riemann describe las distancias y áreas "en pequeño" en cada carta local. En cada carta local se da una métrica de Riemann asignando suavemente una matriz definida positiva de 2×2 a cada punto; cuando se toma una carta diferente, la matriz se transforma de acuerdo con la matriz jacobiana del cambio de coordenadas. La variedad tiene entonces la estructura de una variedad de Riemann bidimensional .

Operador de forma

Wilhelm Blaschke (1885-1962)

La diferencial dn de la función de Gauss n se puede utilizar para definir un tipo de curvatura extrínseca, conocida como operador de forma ^[55] o función de Weingarten . Este operador apareció por primera vez de forma implícita en el trabajo de Wilhelm Blaschke y más tarde de forma explícita en un tratado de Burali-Forti y Burgati. ^[56] Dado que en cada punto x de la superficie, el espacio tangente es un espacio de producto interno , el operador de forma S _x se puede definir como un operador lineal en este espacio mediante la fórmula

${\displaystyle (S_{x}v,w)=(dn(v),w)}$

para los vectores tangentes v , w (el producto interno tiene sentido porque dn ( v ) y w se encuentran ambos en E ³ ). ^[c] El lado derecho es simétrico en v y w , por lo que el operador de forma es autoadjunto en el espacio tangente. Los valores propios de S _x son simplemente las curvaturas principales k ₁ y k ₂ en x . En particular, el determinante del operador de forma en un punto es la curvatura gaussiana, pero también contiene otra información, ya que la curvatura media es la mitad de la traza del operador de forma. La curvatura media es un invariante extrínseco. En geometría intrínseca, un cilindro es desarrollable, lo que significa que cada parte de él es intrínsecamente indistinguible de una parte de un plano ya que su curvatura de Gauss se desvanece de manera idéntica. Sin embargo, su curvatura media no es cero; por lo tanto, extrínsecamente es diferente de un plano.

De manera equivalente, el operador de forma se puede definir como un operador lineal en espacios tangentes, S _p :  T _p M → T _p M . Si n es un campo normal unitario a M y v es un vector tangente, entonces

${\displaystyle S(v)=\pm \nabla _{v}n}$

(no existe un acuerdo estándar sobre si utilizar + o − en la definición).

En general, los vectores propios y los valores propios del operador de forma en cada punto determinan las direcciones en las que se dobla la superficie en cada punto. Los valores propios corresponden a las curvaturas principales de la superficie y los vectores propios son las direcciones principales correspondientes. Las direcciones principales especifican las direcciones que debe recorrer una curva incrustada en la superficie para tener una curvatura máxima y mínima, que vienen dadas por las curvaturas principales.

Curvas geodésicas sobre una superficie

Las curvas de una superficie que minimizan la longitud entre los puntos extremos se denominan geodésicas ; son la forma que adoptaría una banda elástica estirada entre los dos puntos. Matemáticamente se describen utilizando ecuaciones diferenciales ordinarias y el cálculo de variaciones . La geometría diferencial de superficies gira en torno al estudio de las geodésicas. Todavía es una cuestión abierta si cada métrica de Riemann en un mapa local bidimensional surge de una incrustación en un espacio euclidiano tridimensional: la teoría de las geodésicas se ha utilizado para demostrar que esto es cierto en el caso importante en que los componentes de la métrica son analíticos .

Geodésicas

Un triángulo geodésico sobre la esfera. Las geodésicas son arcos de círculo máximo .

Dada una trayectoria suave por partes c ( t ) = ( x ( t ), y ( t )) en el gráfico para t en [ a , b ] , su longitud está definida por

${\displaystyle L(c)=\int _{a}^{b}(E{\dot {x}}^{2}+2F{\dot {x}}{\dot {y}}+G{\dot {y}}^{2})^{\frac {1}{2}}\,dt}$

y energía por

${\displaystyle E(c)=\int _{a}^{b}(E{\dot {x}}^{2}+2F{\dot {x}}{\dot {y}}+G{\dot {y}}^{2})\,dt.}$

La longitud es independiente de la parametrización de un camino. Por las ecuaciones de Euler-Lagrange , si c ( t ) es una longitud que minimiza el camino, parametrizada por arclength , debe satisfacer las ecuaciones de Euler

${\displaystyle {\ddot {x}}+\Gamma _{11}^{1}{\dot {x}}^{2}+2\Gamma _{12}^{1}{\dot {x}}{\dot {y}}+\Gamma _{22}^{1}{\dot {y}}^{2}=0}$

${\displaystyle {\ddot {y}}+\Gamma _{11}^{2}{\dot {x}}^{2}+2\Gamma _{12}^{2}{\dot {x}}{\dot {y}}+\Gamma _{22}^{2}{\dot {y}}^{2}=0}$

donde los símbolos de Christoffel Γ^yo
_ijson dados por

${\displaystyle \Gamma _{ij}^{k}={\tfrac {1}{2}}g^{km}(\partial _{j}g_{im}+\partial _{i}g_{jm}-\partial _{m}g_{ij})}$

donde g ₁₁ = E , g ₁₂ = F , g ₂₂ = G y g ^ij es la matriz inversa de g _ij . Una trayectoria que satisface las ecuaciones de Euler se denomina geodésica . Por la desigualdad de Cauchy-Schwarz una trayectoria que minimiza la energía es simplemente una geodésica parametrizada por la longitud del arco; y, para cualquier geodésica, el parámetro t es proporcional a la longitud del arco. ^[57]

Curvatura geodésica

La curvatura geodésica k _g en un punto de una curva c ( t ) , parametrizada por la longitud del arco, sobre una superficie orientada se define como ^[58]

${\displaystyle k_{g}={\ddot {c}}(t)\cdot \mathbf {n} (t).}$

donde n ( t ) es la normal unitaria "principal" a la curva en la superficie, construida rotando el vector tangente unitario ċ ( t ) a través de un ángulo de +90°.

• La curvatura geodésica en un punto es una invariante intrínseca que depende únicamente de la métrica cerca del punto.
• Una curva de velocidad unitaria en una superficie es geodésica si y solo si su curvatura geodésica se desvanece en todos los puntos de la curva.
• Una curva de velocidad unitaria c ( t ) en una superficie incrustada es una geodésica si y solo si su vector de aceleración c̈ ( t ) es normal a la superficie.

La curvatura geodésica mide de forma precisa qué tan lejos está una curva en la superficie de ser geodésica.

Coordenadas ortogonales

Cuando F = 0 en todo el diagrama de coordenadas, como en el caso de las coordenadas polares geodésicas que se analizan a continuación, las imágenes de las líneas paralelas a los ejes x e y son ortogonales y proporcionan coordenadas ortogonales . Si H = ( EG ) ^{1 ⁄ 2} , entonces la curvatura gaussiana está dada por ^[59]

${\displaystyle K=-{1 \over 2H}\left[\partial _{x}\left({\frac {G_{x}}{H}}\right)+\partial _{y}\left({\frac {E_{y}}{H}}\right)\right].}$

Si además E = 1 , de modo que H = G ^{1 ⁄ 2} , entonces el ángulo φ en la intersección entre la geodésica ( x ( t ), y ( t )) y la recta y = constante viene dado por la ecuación

${\displaystyle \tan \varphi =H\cdot {\frac {\dot {y}}{\dot {x}}}.}$

La derivada de φ viene dada por una fórmula de derivada clásica de Gauss: ^[60]

${\displaystyle {\dot {\varphi }}=-H_{x}\cdot {\dot {y}}.}$

Coordenadas polares geodésicas

Carl Jacobi (1804-1851)

Líneas de contorno que siguen el movimiento de puntos en una curva fija que se mueven a lo largo de geodésicas hacia un punto base

Una vez que se da una métrica en una superficie y se fija un punto base, existe una geodésica única que conecta el punto base con cada punto suficientemente cercano. La dirección de la geodésica en el punto base y la distancia determinan de manera única el otro punto final. Estos dos bits de datos, una dirección y una magnitud, determinan así un vector tangente en el punto base. El mapa de vectores tangentes a puntos finales barre suavemente un vecindario del punto base y define lo que se llama el mapa exponencial , que define un gráfico de coordenadas local en ese punto base. El vecindario barrido tiene propiedades similares a las bolas en el espacio euclidiano, es decir, dos puntos cualesquiera en él están unidos por una geodésica única. Esta propiedad se llama "convexidad geodésica" y las coordenadas se llaman coordenadas normales . El cálculo explícito de las coordenadas normales se puede lograr considerando la ecuación diferencial satisfecha por las geodésicas. Las propiedades de convexidad son consecuencias del lema de Gauss y sus generalizaciones. En términos generales, este lema establece que las geodésicas que comienzan en el punto base deben cortar las esferas de radio fijo centradas en el punto base en ángulos rectos. Las coordenadas polares geodésicas se obtienen combinando el mapa exponencial con coordenadas polares en vectores tangentes en el punto base. La curvatura gaussiana de la superficie se da entonces por la desviación de segundo orden de la métrica en el punto con respecto a la métrica euclidiana. En particular, la curvatura gaussiana es un invariante de la métrica, el célebre Theorema Egregium de Gauss . Una forma conveniente de entender la curvatura proviene de una ecuación diferencial ordinaria, considerada primero por Gauss y luego generalizada por Jacobi, que surge del cambio de coordenadas normales sobre dos puntos diferentes. La ecuación de Gauss-Jacobi proporciona otra forma de calcular la curvatura gaussiana. Geométricamente, explica lo que sucede con las geodésicas desde un punto base fijo a medida que el punto final varía a lo largo de un pequeño segmento de curva a través de datos registrados en el campo de Jacobi , un campo vectorial a lo largo de la geodésica. ^[61] Un siglo y cuarto después de Gauss y Jacobi, Marston Morse dio una interpretación más conceptual del campo de Jacobi en términos de segundas derivadas de la función de energía en la variedad de caminos de Hilbert de dimensión infinita. ^[62]

Mapa exponencial

La teoría de ecuaciones diferenciales ordinarias muestra que si f ( t , v ) es suave entonces la ecuación diferencial ⁠Vuelta al futuro/es⁠ = f ( t , v ) con condición inicial v (0) = v ₀ tiene una solución única para | t | suficientemente pequeña y la solución depende suavemente de t y v ₀ . Esto implica que para vectores tangentes v suficientemente pequeños en un punto dado p = ( x ₀ , y ₀ ) , existe una geodésica c _v ( t ) definida en (−2, 2) con c _v (0) = ( x ₀ , y ₀ ) y ċ _v (0) = v . Además, si | s | ≤ 1 , entonces c _sv = c _v ( st ) . La función exponencial se define por

exp _p ( v ) = c _v (1)

y da un difeomorfismo entre un disco ‖ v ‖ < δ y un entorno de p ; más generalmente, el mapa que envía ( p , v ) a exp _p ( v ) da un difeomorfismo local sobre un entorno de ( p , p ) . El mapa exponencial da coordenadas normales geodésicas cerca de p . ^[63]

Cálculo de coordenadas normales

Existe una técnica estándar (véase por ejemplo Berger (2004)) para calcular el cambio de variables a coordenadas normales u , v en un punto como una expansión formal de la serie de Taylor . Si las coordenadas x , y en (0,0) son localmente ortogonales, escriba

x ( u , v ) = αu + L ( u , v ) + λ ( u , v ) + …

y ( u , v ) = βv + M ( u , v ) + μ ( u , v ) +…

donde L , M son polinomios homogéneos cuadráticos y λ , μ cúbicos en u y v . Si u y v son fijos, x ( t ) = x ( tu , tv ) e y ( t ) = y ( tu , tv ) pueden considerarse como soluciones formales en serie de potencias de las ecuaciones de Euler: esto determina de forma única α , β , L , M , λ y μ .

Lema de Gauss

En coordenadas polares geodésicas, las geodésicas que irradian desde el origen cortan los círculos de radio constante ortogonalmente. Las distancias a lo largo de los radios son distancias verdaderas, pero en los círculos concéntricos los arcos pequeños tienen una longitud H ( r , θ ) = G ( r , θ ) ^{1 ⁄ 2} veces el ángulo que subtienden.

En estas coordenadas la matriz g ( x ) satisface g (0) = I y las rectas t ↦ tv son geodésicas a través de 0. Las ecuaciones de Euler implican la ecuación matricial

g ( v ) v = v ,

Un resultado clave, generalmente llamado lema de Gauss . Geométricamente, establece que

Tomando coordenadas polares ( r , θ ) , se deduce que la métrica tiene la forma

ds ² = dr ² + GRAMO ( r , θ ) dθ ² .

En coordenadas geodésicas, es fácil comprobar que las geodésicas que pasan por cero minimizan la longitud. La topología en la variedad de Riemann está dada entonces por una función de distancia d ( p , q ) , es decir, el ínfimo de las longitudes de las trayectorias suaves por partes entre p y q . Esta distancia se realiza localmente mediante geodésicas, de modo que en coordenadas normales d (0, v ) = ‖ v ‖ . Si el radio δ se toma lo suficientemente pequeño, una ligera agudización del lema de Gauss muestra que la imagen U del disco ‖ v ‖ < δ bajo la función exponencial es geodésicamente convexa , es decir, dos puntos cualesquiera en U están unidos por una geodésica única que se encuentra completamente dentro de U . ^{[64] [65]}

Teorema Egregium

Enunciado original del Theorema Egregium de Gauss, traducido del latín al inglés.

El Teorema Egregium de Gauss , el "Teorema notable", muestra que la curvatura gaussiana de una superficie se puede calcular únicamente en términos de la métrica y, por lo tanto, es un invariante intrínseco de la superficie, independiente de cualquier incrustación isométrica en E ³ y que no cambia bajo transformaciones de coordenadas. En particular, las isometrías y las isometrías locales de superficies preservan la curvatura gaussiana. ^[66]

Este teorema se puede expresar en términos de la expansión en serie de potencias de la métrica, ds , que se da en coordenadas normales ( u , v ) como

ds ² = du ² + dv ² − K ( u dv – v du ) ² /12 +… .

Ecuación de Gauss-Jacobi

Tomando un cambio de coordenadas desde las coordenadas normales en p a las coordenadas normales en un punto cercano q , se obtiene la ecuación de Sturm-Liouville satisfecha por H ( r , θ ) = G ( r , θ ) ^{1 ⁄ 2} , descubierta por Gauss y luego generalizada por Jacobi ,

H _rr = – KH .

El jacobiano de este cambio de coordenadas en q es igual a H _r . Esto proporciona otra forma de establecer la naturaleza intrínseca de la curvatura gaussiana. Debido a que H ( r , θ ) puede interpretarse como la longitud del elemento de línea en la dirección θ , la ecuación de Gauss-Jacobi muestra que la curvatura gaussiana mide la dispersión de las geodésicas en una superficie geométrica a medida que se alejan de un punto. ^[67]

Operador de Laplace-Beltrami

Sobre una superficie con métrica local

${\displaystyle ds^{2}=E\,dx^{2}+2F\,dx\,dy+G\,dy^{2}}$

y operador de Laplace-Beltrami

${\displaystyle \Delta f={1 \over H}\left(\partial _{x}{G \over H}\partial _{x}f-\partial _{x}{F \over H}\partial _{y}f-\partial _{y}{F \over H}\partial _{x}f+\partial _{y}{E \over H}\partial _{y}f\right),}$

donde H ² = EG − F ² , la curvatura gaussiana en un punto viene dada por la fórmula ^[68]

${\displaystyle K=-3\lim _{r\rightarrow 0}\Delta (\log r),}$

donde r denota la distancia geodésica desde el punto.

En coordenadas isotérmicas , consideradas por primera vez por Gauss, se requiere que la métrica tenga la forma especial

${\displaystyle ds^{2}=e^{\varphi }(dx^{2}+dy^{2}).\,}$

En este caso el operador de Laplace-Beltrami viene dado por

${\displaystyle \Delta =e^{-\varphi }\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}\right)}$

y φ satisface la ecuación de Liouville ^[69]

${\displaystyle \Delta \varphi =-2K.\,}$

Se sabe que existen coordenadas isotérmicas en las proximidades de cualquier punto de la superficie, aunque todas las pruebas realizadas hasta la fecha se basan en resultados no triviales sobre ecuaciones diferenciales parciales . ^[70] Existe una prueba elemental para superficies mínimas. ^[71]

Teorema de Gauss-Bonnet

Una triangulación del toro

En una esfera o un hiperboloide , el área de un triángulo geodésico , es decir, un triángulo cuyos lados son todos geodésicos, es proporcional a la diferencia de la suma de los ángulos interiores y π . La constante de proporcionalidad es simplemente la curvatura gaussiana, una constante para estas superficies. Para el toro, la diferencia es cero, lo que refleja el hecho de que su curvatura gaussiana es cero. Estos son resultados estándar en trigonometría esférica, hiperbólica y de secundaria (ver más abajo). Gauss generalizó estos resultados a una superficie arbitraria al demostrar que la integral de la curvatura gaussiana sobre el interior de un triángulo geodésico también es igual a esta diferencia o exceso de ángulo. Su fórmula demostró que la curvatura gaussiana podía calcularse cerca de un punto como el límite del área sobre el exceso de ángulo para triángulos geodésicos que se encogen hasta el punto. Dado que cualquier superficie cerrada puede descomponerse en triángulos geodésicos, la fórmula también podría usarse para calcular la integral de la curvatura sobre toda la superficie. Como caso especial de lo que ahora se llama el teorema de Gauss-Bonnet , Gauss demostró que esta integral era notablemente siempre 2π veces un entero, un invariante topológico de la superficie llamado característica de Euler . Este invariante es fácil de calcular combinatoriamente en términos del número de vértices, aristas y caras de los triángulos en la descomposición, también llamada triangulación . Esta interacción entre análisis y topología fue la precursora de muchos resultados posteriores en geometría, que culminaron en el teorema del índice de Atiyah-Singer . En particular, las propiedades de la curvatura imponen restricciones a la topología de la superficie.

Triángulos geodésicos

Gauss demostró que, si Δ es un triángulo geodésico en una superficie con ángulos α , β y γ en los vértices A , B y C , entonces

${\displaystyle \int _{\Delta }K\,dA=\alpha +\beta +\gamma -\pi .}$

De hecho, tomando coordenadas polares geodésicas con origen A y AB , AC los radios en ángulos polares 0 y α :

${\displaystyle {\begin{aligned}\int _{\Delta }K\,dA&=\int _{\Delta }KH\,dr\,d\theta =-\int _{0}^{\alpha }\int _{0}^{r_{\theta }}\!H_{rr}\,dr\,d\theta \\&=\int _{0}^{\alpha }1-H_{r}(r_{\theta },\theta )\,d\theta =\int _{0}^{\alpha }d\theta +\int _{\pi -\beta }^{\gamma }\!\!d\varphi \\&=\alpha +\beta +\gamma -\pi ,\end{aligned}}}$

donde la segunda igualdad se desprende de la ecuación de Gauss-Jacobi y la cuarta de la fórmula de la derivada de Gauss en las coordenadas ortogonales ( r , θ ) .

La fórmula de Gauss muestra que la curvatura en un punto se puede calcular como el límite del exceso de ángulo α + β + γ − π sobre el área para triángulos geodésicos sucesivamente más pequeños cerca del punto. Cualitativamente, una superficie es positiva o negativamente curvada según el signo del exceso de ángulo para triángulos geodésicos arbitrariamente pequeños. ^[49]

Teorema de Gauss-Bonnet

La característica de Euler de una esfera, triangulada como un icosaedro , es V − E + F = 12 − 30 + 20 = 2 .

Dado que cada 2-variedad orientada compacta M puede triangularse mediante pequeños triángulos geodésicos, se deduce que

${\displaystyle \int _{M}KdA=2\pi \,\chi (M)}$

donde χ ( M ) denota la característica de Euler de la superficie.

De hecho, si hay F caras, E aristas y V vértices, entonces 3 F = 2 E y el lado izquierdo es igual a 2π V – π F = 2π( V – E + F ) = 2π χ ( M ) .

Este es el célebre teorema de Gauss-Bonnet : demuestra que la integral de la curvatura gaussiana es un invariante topológico de la variedad, es decir, la característica de Euler. Este teorema puede interpretarse de muchas maneras; quizás una de las de mayor alcance ha sido como el teorema del índice para un operador diferencial elíptico en M , uno de los casos más simples del teorema del índice de Atiyah-Singer . Otro resultado relacionado, que puede demostrarse utilizando el teorema de Gauss-Bonnet, es el teorema del índice de Poincaré-Hopf para campos vectoriales en M que se anulan solo en un número finito de puntos: la suma de los índices en estos puntos es igual a la característica de Euler, donde el índice de un punto se define de la siguiente manera: en un pequeño círculo alrededor de cada cero aislado, el campo vectorial define una función en el círculo unitario; el índice es simplemente el número de vueltas de esta función.) ^{[49] [72] [73]}

Curvatura e incrustaciones

Si la curvatura gaussiana de una superficie M es positiva en todas partes, entonces la característica de Euler es positiva, por lo que M es homeomorfa (y por lo tanto difeomorfa) a S ² . Si además la superficie está isométricamente incrustada en E ³ , la función de Gauss proporciona un difeomorfismo explícito. Como observó Hadamard , en este caso la superficie es convexa ; este criterio de convexidad puede verse como una generalización bidimensional del conocido criterio de segunda derivada para la convexidad de curvas planas. Hilbert demostró que toda superficie cerrada isométricamente incrustada debe tener un punto de curvatura positiva. Por lo tanto, una 2-variedad riemanniana cerrada de curvatura no positiva nunca puede estar incrustada isométricamente en E ³ ; sin embargo, como mostró Adriano Garsia utilizando la ecuación de Beltrami para aplicaciones cuasiconformales , esto siempre es posible para alguna métrica conformemente equivalente . ^[74]

Superficies de curvatura constante

Las superficies simplemente conexas de curvatura constante 0, +1 y –1 son el plano euclidiano, la esfera unidad en E ³ , y el plano hiperbólico . Cada una de ellas tiene un grupo de Lie tridimensional transitivo de isometrías que preservan la orientación G , que puede utilizarse para estudiar su geometría. Cada una de las dos superficies no compactas puede identificarse con el cociente G / K donde K es un subgrupo compacto maximal de G . Aquí K es isomorfo a SO(2) . Cualquier otra 2-variedad riemanniana cerrada M de curvatura gaussiana constante, después de escalar la métrica por un factor constante si es necesario, tendrá una de estas tres superficies como su espacio de recubrimiento universal . En el caso orientable, el grupo fundamental Γ de M puede identificarse con un subgrupo uniforme libre de torsión de G y M puede entonces identificarse con el espacio de doble clase lateral Γ \ G / K . En el caso de la esfera y el plano euclidiano, los únicos ejemplos posibles son la esfera misma y los toros obtenidos como cocientes de R ² por subgrupos discretos de rango 2. Para superficies cerradas de género g ≥ 2 , el espacio de módulos de superficies de Riemann obtenido cuando Γ varía en todos esos subgrupos, tiene dimensión real 6 g − 6 . ^[75] Por el teorema de uniformización de Poincaré , cualquier 2-variedad cerrada orientable es conformemente equivalente a una superficie de curvatura constante 0, +1 o –1. En otras palabras, al multiplicar la métrica por un factor de escala positivo, se puede hacer que la curvatura gaussiana tome exactamente uno de estos valores (el signo de la característica de Euler de M ). ^[76]

Geometría euclidiana

Un triangulo en el plano

En el caso del plano euclidiano, el grupo de simetría es el grupo de movimiento euclidiano , el producto semidirecto del grupo bidimensional de traslaciones por el grupo de rotaciones. ^[77] Las geodésicas son líneas rectas y la geometría está codificada en las fórmulas elementales de trigonometría , como la regla del coseno para un triángulo con lados a , b , c y ángulos α , β , γ :

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\,\cos \gamma .}$

Los toros planos se pueden obtener tomando el cociente de R ² por una red , es decir, un subgrupo abeliano libre de rango 2. Estas superficies cerradas no tienen incrustaciones isométricas en E ³ . Sin embargo, admiten incrustaciones isométricas en E ⁴ ; en el caso más fácil esto se deduce del hecho de que el toro es un producto de dos círculos y cada círculo puede incrustarse isométricamente en E ² . ^[78]

Geometría esférica

Un triángulo esférico

El área de un triángulo esférico en la esfera unitaria es α + β + γ − π .

El grupo de isometría de la esfera unitaria S ² en E ³ es el grupo ortogonal O(3) , con el grupo de rotación SO(3) como el subgrupo de isometrías que preservan la orientación. Es el producto directo de SO(3) con la función antípoda , enviando x a – x ​​. ^[79] El grupo SO(3) actúa transitivamente sobre S ² . El subgrupo estabilizador del vector unitario (0,0,1) se puede identificar con SO(2) , de modo que S ² = SO(3)/SO(2) .

Las geodésicas entre dos puntos de la esfera son los arcos de círculo máximo con estos puntos finales dados. Si los puntos no son antípodas, existe una única geodésica más corta entre los puntos. Las geodésicas también se pueden describir en grupo teóricamente: cada geodésica que pasa por el polo norte (0,0,1) es la órbita del subgrupo de rotaciones alrededor de un eje que pasa por puntos antípodas en el ecuador.

Un triángulo esférico es un triángulo geodésico sobre la esfera. Está definido por los puntos A , B , C sobre la esfera con lados BC , CA , AB formados a partir de arcos de círculo máximo de longitud menor que π . Si las longitudes de los lados son a , b , c y los ángulos entre los lados α , β , γ , entonces la ley del coseno esférico establece que

${\displaystyle \cos c=\cos a\,\cos b+\sin a\,\sin b\,\cos \gamma .}$

El área del triángulo está dada por

Área = α + β + γ − π .

Utilizando la proyección estereográfica desde el polo norte, la esfera puede identificarse con el plano complejo extendido C ∪ {∞} . La función explícita está dada por

${\displaystyle \pi (x,y,z)={x+iy \over 1-z}\equiv u+iv.}$

Bajo esta correspondencia cada rotación de S ² corresponde a una transformación de Möbius en SU(2) , única hasta el signo. ^[80] Con respecto a las coordenadas ( u , v ) en el plano complejo, la métrica esférica se convierte en ^[81]

${\displaystyle ds^{2}={4(du^{2}+dv^{2}) \over (1+u^{2}+v^{2})^{2}}.}$

La esfera unidad es la única superficie orientable cerrada con curvatura constante +1. El cociente SO(3)/O(2) puede identificarse con el plano proyectivo real . No es orientable y puede describirse como el cociente de S ² por la función antípoda (multiplicación por −1). La esfera es simplemente conexa, mientras que el plano proyectivo real tiene grupo fundamental Z ₂ . Los subgrupos finitos de SO(3) , correspondientes a los subgrupos finitos de O(2) y los grupos de simetría de los sólidos platónicos , no actúan libremente sobre S ² , por lo que los cocientes correspondientes no son 2-variedades, solo orbifolds .

Geometría hiperbólica

Henri Poincaré (1854-1912)

La geometría no euclidiana ^[82] se discutió por primera vez en cartas de Gauss, quien realizó extensos cálculos a principios del siglo XIX que, aunque circularon en forma privada, decidió no publicar. En 1830, Lobachevsky e independientemente en 1832 Bolyai , el hijo de uno de los corresponsales de Gauss, publicaron versiones sintéticas de esta nueva geometría, por las que fueron severamente criticados. Sin embargo, no fue hasta 1868 que Beltrami, seguido por Klein en 1871 y Poincaré en 1882, dieron modelos analíticos concretos para lo que Klein denominó geometría hiperbólica . Los cuatro modelos de geometría hiperbólica bidimensional que surgieron fueron:

• el modelo de Beltrami-Klein ;
• el disco de Poincaré ;
• el semiplano superior de Poincaré ;
• El modelo hiperboloide de Wilhelm Killing en el espacio tridimensional de Minkowski .

El primer modelo, basado en un disco, tiene la ventaja de que las geodésicas son en realidad segmentos de línea (es decir, intersecciones de líneas euclidianas con el disco unitario abierto). El último modelo tiene la ventaja de que proporciona una construcción que es completamente paralela a la de la esfera unitaria en el espacio euclidiano tridimensional. Sin embargo, debido a su aplicación en análisis y geometría complejos, los modelos de Poincaré son los más utilizados: son intercambiables gracias a las transformaciones de Möbius entre el disco y el semiplano superior.

Dejar

${\displaystyle D=\{z\,\colon |z|<1\}}$

sea ​​el disco de Poincaré en el plano complejo con métrica de Poincaré

${\displaystyle ds^{2}={4(dx^{2}+dy^{2}) \over (1-x^{2}-y^{2})^{2}}.}$

En coordenadas polares ( r , θ ) la métrica viene dada por

${\displaystyle ds^{2}={4(dr^{2}+r^{2}\,d\theta ^{2}) \over (1-r^{2})^{2}}.}$

La longitud de una curva γ :[ a , b ] → D viene dada por la fórmula

${\displaystyle \ell (\gamma )=\int _{a}^{b}{2|\gamma ^{\prime }(t)|\,dt \over 1-|\gamma (t)|^{2}}.}$

El grupo G = SU(1,1) dado por

${\displaystyle G=\left\{{\begin{pmatrix}\alpha &\beta \\{\overline {\beta }}&{\overline {\alpha }}\end{pmatrix}}:\alpha ,\beta \in \mathbf {C} ,\,|\alpha |^{2}-|\beta |^{2}=1\right\}}$

actúa transitivamente por transformaciones de Möbius sobre D y el subgrupo estabilizador de 0 es el grupo de rotación

${\displaystyle K=\left\{{\begin{pmatrix}\zeta &0\\0&{\overline {\zeta }}\end{pmatrix}}:\zeta \in \mathbf {C} ,\,|\zeta |=1\right\}.}$

El grupo cociente SU(1,1)/± I es el grupo de isometrías de D que preservan la orientación . Dos puntos cualesquiera z , w en D están unidos por una geodésica única, dada por la porción del círculo o línea recta que pasa por z y w y es ortogonal al círculo límite. La distancia entre z y w está dada por

${\displaystyle d(z,w)=2\tanh ^{-1}{\frac {|z-w|}{|1-{\overline {w}}z|}}.}$

En particular, d (0, r ) = 2 tanh ⁻¹ r y c ( t ) = ⁠1/2⁠ tanh t es la geodésica que pasa por 0 a lo largo del eje real, parametrizada por la longitud del arco.

La topología definida por esta métrica es equivalente a la topología euclidiana habitual, aunque como espacio métrico ( D , d ) es completo.

Un triángulo hiperbólico en el modelo del disco de Poincaré

Un triángulo hiperbólico es un triángulo geodésico para esta métrica: tres puntos cualesquiera en D son vértices de un triángulo hiperbólico. Si los lados tienen longitud a , b , c con ángulos correspondientes α , β , γ , entonces la regla del coseno hiperbólico establece que

${\displaystyle \cosh c=\cosh a\,\cosh b-\sinh a\,\sinh b\,\cos \gamma .}$

El área del triángulo hiperbólico está dada por ^[83]

Área = π – α – β – γ .

El disco unitario y el semiplano superior

${\displaystyle H=\{w=x+iy\,\colon \,y>0\}}$

son conformemente equivalentes por las transformaciones de Möbius

${\displaystyle w=i{1+z \over 1-z},\,\,z={w-i \over w+i}.}$

Bajo esta correspondencia la acción de SL(2,R) por transformaciones de Möbius sobre H corresponde a la de SU(1,1) sobre D . La métrica sobre H se convierte en

${\displaystyle ds^{2}={dx^{2}+dy^{2} \over y^{2}}.}$

Dado que las líneas o círculos se conservan bajo las transformaciones de Möbius, las geodésicas se describen nuevamente mediante líneas o círculos ortogonales al eje real.

El disco unitario con la métrica de Poincaré es la única variedad de Riemann orientada, bidimensional y simplemente conexa con curvatura constante −1. Cualquier superficie cerrada orientada M con esta propiedad tiene a D como su espacio de recubrimiento universal. Su grupo fundamental puede identificarse con un subgrupo concompacto libre de torsión Γ de SU(1,1) , de tal manera que

${\displaystyle M=\Gamma \backslash G/K.}$

En este caso Γ es un grupo finitamente presentado . Los generadores y relaciones están codificados en un polígono geodésico fundamental geodésico convexo en D (o H ) que corresponde geométricamente a geodésicas cerradas en M.

Ejemplos .

• la superficie de Bolza del género 2;
• el cuartico de Klein del género 3;
• la superficie Macbeath del género 7;
• El primer triplete de Hurwitz del género 14.

Uniformización

Dada una superficie cerrada orientada M con curvatura gaussiana K , la métrica de M se puede cambiar conformemente escalándola por un factor e ^{2 u} . La nueva curvatura gaussiana K′ viene dada entonces por

${\displaystyle K^{\prime }(x)=e^{-2u}(K(x)-\Delta u),}$

donde Δ es el laplaciano de la métrica original. Por lo tanto, para demostrar que una superficie dada es conformemente equivalente a una métrica con curvatura constante K′, basta con resolver la siguiente variante de la ecuación de Liouville :

${\displaystyle \Delta u=K^{\prime }e^{2u}+K(x).}$

Cuando M tiene característica de Euler 0, entonces es difeomorfo a un toro , K′ = 0 , por lo que esto equivale a resolver

${\displaystyle \Delta u=K(x).}$

Según la teoría elíptica estándar, esto es posible porque la integral de K sobre M es cero, según el teorema de Gauss-Bonnet. ^[84]

Cuando M tiene característica de Euler negativa, K′ = −1 , por lo que la ecuación a resolver es:

${\displaystyle \Delta u=-e^{2u}+K(x).}$

Utilizando la continuidad del mapa exponencial en el espacio de Sobolev debido a Neil Trudinger , esta ecuación no lineal siempre se puede resolver. ^[85]

Finalmente en el caso de la 2-esfera, K′ = 1 y la ecuación se convierte en:

${\displaystyle \Delta u=e^{2u}+K(x).}$

Hasta ahora esta ecuación no lineal no ha sido analizada directamente, aunque resultados clásicos como el teorema de Riemann-Roch implican que siempre tiene una solución. ^[86] El método de flujo de Ricci , desarrollado por Richard S. Hamilton , proporciona otra prueba de existencia basada en ecuaciones diferenciales parciales no lineales para demostrar la existencia. ^[87] De hecho, el flujo de Ricci en métricas conformes en S ² se define en funciones u ( x , t ) por

${\displaystyle u_{t}=4\pi -K'(x,t)=4\pi -e^{-2u}(K(x)-\Delta u).}$

Después de un tiempo finito, Chow demostró que K′ se vuelve positivo; los resultados previos de Hamilton podrían entonces usarse para demostrar que K′ converge a +1. ^[88] Antes de estos resultados sobre el flujo de Ricci, Osgood, Phillips y Sarnak (1988) habían dado un enfoque alternativo y técnicamente más simple para la uniformización basado en el flujo en métricas de Riemann g definidas por log det Δ _g .

Una prueba que utiliza operadores elípticos, descubierta en 1988, se puede encontrar en Ding (2001). Sea G la función de Green en S ² que satisface Δ G = 1 + 4π δ _P , donde δ _P es la medida puntual en un punto fijo P de S ² . La ecuación Δ v = 2 K – 2 , tiene una solución suave v , porque el lado derecho tiene integral 0 por el teorema de Gauss-Bonnet. Por lo tanto φ = 2 G + v satisface Δ φ = 2 K lejos de P . Se deduce que g ₁ = e ^φ g es una métrica completa de curvatura constante 0 en el complemento de P , que es por lo tanto isométrica al plano. Componiendo con proyección estereográfica , se deduce que hay una función suave u tal que e ^{2 u} g tiene curvatura gaussiana +1 en el complemento de P . La función u se extiende automáticamente a una función suave sobre todo S ² . ^[d]

Conexión riemanniana y transporte paralelo

Tulio Levi-Civita (1873-1941)

El enfoque clásico de Gauss para la geometría diferencial de superficies fue el enfoque elemental estándar ^[89] que precedió a la aparición de los conceptos de variedad de Riemann iniciados por Bernhard Riemann a mediados del siglo XIX y de conexión desarrollados por Tullio Levi-Civita , Élie Cartan y Hermann Weyl a principios del siglo XX. La noción de conexión, derivada covariante y transporte paralelo proporcionó una forma más conceptual y uniforme de entender la curvatura, que no solo permitió generalizaciones a variedades de dimensiones superiores sino que también proporcionó una herramienta importante para definir nuevos invariantes geométricos, llamados clases características . ^[90] El enfoque que utiliza derivadas covariantes y conexiones es actualmente el adoptado en libros de texto más avanzados. ^[91]

Derivada covariante

Las conexiones en una superficie se pueden definir desde varios puntos de vista equivalentes pero igualmente importantes. La conexión de Riemann o conexión de Levi-Civita ^[92] se entiende quizás más fácilmente en términos de elevación de campos vectoriales , considerados como operadores diferenciales de primer orden que actúan sobre funciones en la variedad, a operadores diferenciales en el fibrado tangente o fibrado de marcos . En el caso de una superficie incrustada, la elevación a un operador en campos vectoriales, llamado derivada covariante , se describe muy simplemente en términos de proyección ortogonal. De hecho, un campo vectorial en una superficie incrustada en R ³ puede considerarse como una función de la superficie en R ³ . Otro campo vectorial actúa como un operador diferencial componente a componente. El campo vectorial resultante no será tangente a la superficie, pero esto se puede corregir tomando su proyección ortogonal sobre el espacio tangente en cada punto de la superficie. Como Ricci y Levi-Civita se dieron cuenta a principios del siglo XX, este proceso depende solo de la métrica y se puede expresar localmente en términos de los símbolos de Christoffel.

Transporte paralelo de un vector alrededor de un triángulo geodésico sobre la esfera. La longitud del vector transportado y el ángulo que forma con cada lado permanecen constantes.

Transporte paralelo

El transporte paralelo de vectores tangentes a lo largo de una curva en la superficie fue el siguiente gran avance en el tema, debido a Levi-Civita . ^[49] Está relacionado con la noción anterior de derivada covariante, porque es la monodromía de la ecuación diferencial ordinaria en la curva definida por la derivada covariante con respecto al vector de velocidad de la curva. El transporte paralelo a lo largo de geodésicas, las "líneas rectas" de la superficie, también se puede describir fácilmente de manera directa. Un vector en el plano tangente se transporta a lo largo de una geodésica como el único campo vectorial con longitud constante y que forma un ángulo constante con el vector de velocidad de la geodésica. Para una curva general, este proceso tiene que modificarse utilizando la curvatura geodésica, que mide cuánto se aleja la curva de ser una geodésica. ^[64]

Se dice que un campo vectorial v ( t ) a lo largo de una curva de velocidad unitaria c ( t ) , con curvatura geodésica k _g ( t ) , es paralelo a lo largo de la curva si

• Tiene longitud constante
• el ángulo θ ( t ) que forma con el vector de velocidad ċ ( t ) satisface

${\displaystyle {\dot {\theta }}(t)=-k_{g}(t)}$

Esto retoma la regla para el transporte paralelo a lo largo de una curva geodésica o geodésica por partes, porque en ese caso k _g = 0 , de modo que el ángulo θ ( t ) debe permanecer constante en cualquier segmento geodésico. La existencia de transporte paralelo se deduce porque θ ( t ) se puede calcular como la integral de la curvatura geodésica. Dado que, por lo tanto, depende continuamente de la norma L ² de k _g , se deduce que el transporte paralelo para una curva arbitraria se puede obtener como el límite del transporte paralelo al aproximar curvas geodésicas por partes. ^[93]

La conexión puede entonces describirse en términos de trayectorias de elevación en la variedad hacia trayectorias en el fibrado de marco tangente u ortonormal, formalizando así la teoría clásica del " marco móvil ", favorecida por los autores franceses. ^[94] Las elevaciones de bucles alrededor de un punto dan lugar al grupo de holonomía en ese punto. La curvatura gaussiana en un punto puede recuperarse a partir del transporte paralelo alrededor de bucles cada vez más pequeños en el punto. Equivalentemente, la curvatura puede calcularse directamente a un nivel infinitesimal en términos de corchetes de Lie de campos vectoriales elevados.

Élie Cartan en 1904

Conexión 1-forma

El enfoque de Cartan y Weyl, utilizando 1-formas de conexión en el fibrado de marcos de M , proporciona una tercera manera de entender la conexión de Riemann. Observaron que el transporte paralelo dicta que un camino en la superficie se eleve a un camino en el fibrado de marcos de modo que sus vectores tangentes se encuentren en un subespacio especial de codimensión uno en el espacio tangente tridimensional del fibrado de marcos. La proyección sobre este subespacio está definida por una 1-forma diferencial en el fibrado de marcos ortonormal, la forma de conexión . Esto permitió que las propiedades de curvatura de la superficie se codificaran en formas diferenciales en el fibrado de marcos y fórmulas que involucraran sus derivadas externas .

Este enfoque es particularmente simple para una superficie embebida. Gracias a un resultado de Kobayashi (1956), la 1-forma de conexión en una superficie embebida en el espacio euclidiano E ³ es simplemente el pullback bajo el mapa de Gauss de la 1-forma de conexión en S ² . ^[95] Usando la identificación de S ² con el espacio homogéneo SO(3)/SO(2) , la 1-forma de conexión es simplemente un componente de la 1-forma de Maurer–Cartan en SO(3) . ^[96]

Geometría diferencial global de superficies

Aunque la caracterización de la curvatura involucra solo la geometría local de una superficie, existen aspectos globales importantes como el teorema de Gauss-Bonnet , el teorema de uniformización , el teorema de von Mangoldt-Hadamard y el teorema de incrustabilidad. Existen otros aspectos importantes de la geometría global de las superficies. ^[97] Estos incluyen:

• Radio de inyectividad , definido como el r más grande tal que dos puntos a una distancia menor que r están unidos por una geodésica única. Wilhelm Klingenberg demostró en 1959 que el radio de inyectividad de una superficie cerrada está limitado por debajo por el mínimo de δ = ⁠π/√ apoyar K⁠ y la longitud de su geodésica cerrada más pequeña. Esto mejoró un teorema de Bonnet que demostró en 1855 que el diámetro de una superficie cerrada de curvatura gaussiana positiva siempre está acotado superiormente por δ ; en otras palabras, una geodésica que realice la distancia métrica entre dos puntos no puede tener una longitud mayor que δ .
• Rigidez . En 1927, Cohn-Vossen demostró que dos ovaloides (superficies cerradas con curvatura gaussiana positiva) que son isométricas son necesariamente congruentes por una isometría de E ³ . Además, una superficie empotrada cerrada con curvatura gaussiana positiva y curvatura media constante es necesariamente una esfera; de la misma manera, una superficie empotrada cerrada de curvatura gaussiana constante debe ser una esfera (Liebmann 1899). Heinz Hopf demostró en 1950 que una superficie empotrada cerrada con curvatura media constante y género 0, es decir, homeomorfa a una esfera, es necesariamente una esfera; cinco años después, Alexandrov eliminó el supuesto topológico. En la década de 1980, Wente construyó toros inmersos de curvatura media constante en el 3-espacio euclidiano.
• Conjetura de Carathéodory : Esta conjetura establece que una superficie cerrada, convexa y tres veces diferenciable, admite al menos dos puntos umbilicales . El primer trabajo sobre esta conjetura fue realizado en 1924 por Hans Hamburger , quien señaló que se deduce de la siguiente afirmación más fuerte: el índice de valor semientero de la foliación de curvatura principal de un umbilical aislado es como máximo uno.
• Curvatura gaussiana cero : una superficie completa en E ³ con curvatura gaussiana cero debe ser un cilindro o un plano.
• Teorema de Hilbert (1901): ninguna superficie completa con curvatura negativa constante puede sumergirse isométricamente en E ³ .

Bucle más corto en un toro

• Conjetura de Willmore . Esta conjetura establece que la integral del cuadrado de la curvatura media de un toro inmerso en E ³ debe estar acotada inferiormente por 2π ² . Se sabe que la integral es invariante de Moebius. Fue resuelta en 2012 por Fernando Codá Marques y André Neves . ^[98]
• Desigualdades isoperimétricas . En 1939 Schmidt demostró que la desigualdad isoperimétrica clásica para curvas en el plano euclidiano es también válida en la esfera o en el plano hiperbólico: es decir, demostró que entre todas las curvas cerradas que delimitan un dominio de área fija, el perímetro se minimiza cuando la curva es un círculo para la métrica. En una dimensión superior, se sabe que entre todas las superficies cerradas en E ³ que surgen como límite de un dominio acotado de volumen unitario, el área superficial se minimiza para una bola euclidiana.
• Desigualdades sistólicas para curvas en superficies . Dada una superficie cerrada, su sístole se define como la longitud más pequeña de cualquier curva cerrada no contráctil en la superficie. En 1949, Loewner demostró una desigualdad del toro para métricas en el toro, a saber, que el área del toro sobre el cuadrado de su sístole está limitada por debajo por ⁠√ 3/2⁠ , con igualdad en el caso plano (curvatura constante). Un resultado similar lo da la desigualdad de Pu para el plano proyectivo real de 1952, con un límite inferior de ⁠2/π⁠ También se logró en el caso de curvatura constante. Para la botella de Klein , Blatter y Bavard obtuvieron posteriormente un límite inferior de ⁠√ 8/π⁠ . Para una superficie cerrada de género g , Hebda y Burago demostraron que la relación está limitada por debajo de ⁠1/2⁠ . Tres años después, Mikhail Gromov encontró un límite inferior dado por una constante multiplicada por g ^{1 ⁄ 2} , aunque esto no es óptimo. Límites superior e inferior asintóticamente precisos dados por constantes multiplicadas por ^{g 1 ⁄} 2 .gramo/(log g ) ²⁠ se deben a Gromov y Buser-Sarnak, y se pueden encontrar en Katz (2007). También existe una versión para métricas en la esfera, tomando para la sístole la longitud de la geodésica cerrada más pequeña . Gromov conjeturó un límite inferior de ⁠1/2 √ 3⁠ en 1980: el mejor resultado hasta ahora es el límite inferior de ⁠1/8⁠ obtenido por Regina Rotman en 2006. ^[99]

Guía de lectura

Una de las indagaciones introductorias más completas sobre el tema, que traza el desarrollo histórico desde antes de Gauss hasta los tiempos modernos, es la de Berger (2004). Se ofrecen descripciones de la teoría clásica en Eisenhart (2004), Kreyszig (1991) y Struik (1988); los libros de texto de pregrado más modernos y profusamente ilustrados de Gray, Abbena y Salamon (2006), Pressley (2001) y Wilson (2008) pueden resultar más accesibles. Se puede encontrar una descripción accesible de la teoría clásica en Hilbert y Cohn-Vossen (1952). Se pueden encontrar tratamientos de nivel de posgrado más sofisticados que utilizan la conexión de Riemann en una superficie en Singer y Thorpe (1967), do Carmo (2016) y O'Neill (2006).

Véase también

• Vector tangente
• Superficie de Zoll

Notas

1. Una superficie lisa es una superficie en la que cada punto tiene una vecindad difeomorfa a algún conjunto abierto en E ² .
2. Una superficie de Riemann es una superficie lisa equipada con una métrica de Riemann.
3. Nótese que en algunos textos más recientes la forma bilineal simétrica del lado derecho se denomina segunda forma fundamental; sin embargo, en general no corresponde a la segunda forma fundamental definida clásicamente.
4. A continuación se presenta un argumento que involucra un teorema de Sacks y Uhlenbeck (1981) sobre singularidades removibles de mapas armónicos de energía finita.

1. Gauss 1902.
2. Struik 1987, págs. 50-53
3. Wells 2017, págs. 17–30
4. Euler 1760
5. Euler 1771
6. Kreyszig 1991
7. Struik 1988
8. Warner 1983
9. Hitchin 2013, pág. 45
10. do Carmo 2016, págs. 54-56
11. Wilson 2008, pág. 115
12. Pressley 2001, págs. 68-77
13. do Carmo 2016, págs. 55
14. do Carmo 2016, págs. 60-65
15. O'Neill 2006, pág. 113
16. Lee "Introducción a los colectores lisos"
17. do Carmo 2016, págs. 72
18. Kreyszig 1991
19. Singer y Thorpe 1967, págs. 100-114
20. Singer y Thorpe 1967, pág. 133-134
21. do Carmo 2016, págs. 155-157
22. Do Carmo, página 235
23. Do Carmo, página 238
24. Do Carmo, páginas 237-238
25. Struik 1988, pág. 112
26. Darboux, vol. III, página 246
27. Berger. Una visión panorámica de la geometría de Riemann.
28. O'Neill 2006, pág. 257
29. do Carmo 2016, págs. 309–314
30. Hitchin 2013, pág. 57
31. do Carmo 2016, pág. 221-222
32. O'Neill 2006, págs. 281-289
33. Hitchin 2013, págs. 57-58
34. do Carmo 2016, pág. 223
35. do Carmo 2016, págs.222-223
36. do Carmo 2016, págs.224-225
37. Do Carmo, página 183
38. Do Carmo, página 242
39. Hitchin 2013
40. Struik 1988
41. O'Neill 2006
42. Spivak, "Una introducción completa a la geometría diferencial, vol. III". Página 157.
43. Spivak, páginas 161-166
44. Spivak, página 168
45. Eisenhart 2004, págs. 228-229
46. Eisenhart 2004, págs. 241-250; do Carmo 2016, págs. 188-197.
47. del Carmo 2016, pág. 194.
48. Eisenhart 2004, págs. 61–65.
49. Eisenhart 2004
50. Eisenhart 2004, págs. 250-269; do Carmo 2016, págs. 197-213.
51. La solución de Douglas se describe en Courant (1950).
52. Eisenhart 2004, págs. 270-291; O'Neill 2006, págs. 249-251; Hilbert y Cohn-Vossen 1952.
53. Stillwell 1996, págs. 1–5.
54. Wilson 2008.
55. O'Neill 2006, págs. 195–216; do Carmo 2016, págs. 134–153; Singer y Thorpe 1967, págs. 216–224.
56. Gray, Abbena y Salamon 2006, pág. 386.
57. Berger 2004; Wilson 2008; Milnor 1963.
58. Eisenhart 2004, pág. 131; Berger 2004, pág. 39; do Carmo 2016, pág. 248; O'Neill 2006, pág. 237
59. Eisenhart 2004; Taylor 1996a, págs. 472–473, Apéndice C.
60. Eisenhart 2004, sección 88; Berger 2004.
61. do Carmo 2016, pág. 357
62. Milnor 1963
63. Wilson 2008
64. Berger 2004
65. do Carmo 2016, págs. 303–305
66. Berger 2004, págs. 41, 61, 123-124
67. O'Neill 2006, pág. 395
68. Helgason 1978, pág. 92
69. O'Neill 2006, pág. 286
70. do Carmo 2016, pág. 227
71. Osserman 2002, págs. 31-32
72. do Carmo 2016, págs. 283–286
73. Thorpe 1994, págs. 201-207
74. Singer y Thorpe 1967; Garsia, Adriano M. (1961), "Una incrustación de superficies de Riemann cerradas en el espacio euclidiano", Comment. Math. Helv. , 35 : 93–110, doi :10.1007/BF02567009, S2CID  120653575
75. Imayoshi y Taniguchi 1992, págs. 47–49
76. Berger 1977; Taylor 1996b.
77. Wilson 2008, págs. 1–23, Capítulo I, Geometría euclidiana .
78. del Carmo 2016.
79. Wilson 2008, págs. 25–49, Capítulo II, Geometría esférica .
80. Wilson 2008, Capítulo 2.
81. Eisenhart 2004, pág. 110.
82. Stillwell 1996; Bonola, Carslaw y Enriques 1955.
83. Wilson 2008, Capítulo 5.
84. Taylor 1996b, pág. 107; Berger 1977, págs. 341–343.
85. Berger 1977, págs. 222-225; Taylor 1996b, págs. 101-108.
86. Taylor 1996b
87. Chow 1991
88. Chen, Lu y Tian (2006) señalaron y corrigieron un paso faltante en el enfoque de Hamilton y Chow; véase también Andrews y Bryan (2010).
89. Eisenhart 2004; Kreyszig 1991; Berger 2004; Wilson 2008.
90. Kobayashi y Nomizu 1969, Capítulo XII.
91. hacer Carmo 2016; O'Neill 2006; Cantante y Thorpe 1967.
92. Levi-Civita 1917
93. Arnold 1989, págs. 301–306, Apéndice I.; Berger 2004, págs. 263–264.
94. Darboux.
95. Kobayashi y Nomizu 1969
96. Ivey y Landsberg 2003.
97. Berger 2004, págs. 145-161; do Carmo 2016; Chern 1967; Hopf 1989.
98. Codá Marques, Fernando; Neves, André (2014). "Teoría de Min-Max y la conjetura de Willmore". Anales de Matemáticas . 179 (2): 683–782. arXiv : 1202.6036 . doi :10.4007/annals.2014.179.2.6. JSTOR  24522767. S2CID  50742102.
99. Rotman, R. (2006) "La longitud de la geodésica cerrada más corta y el área de una esfera bidimensional", Proc. Amer. Math. Soc. 134 : 3041-3047. Croke, Rotman-Nabutovsky y Sabourau habían obtenido límites inferiores anteriores.

Referencias

• Andrews, Ben; Bryan, Paul (2010), "Límites de curvatura por comparación isoperimétrica para flujo de Ricci normalizado en dos esferas", Calc. Var. Partial Differential Equations , 39 (3–4): 419–428, arXiv : 0908.3606 , doi :10.1007/s00526-010-0315-5, S2CID  1095459
• Arnold, VI (1989), Métodos matemáticos de la mecánica clásica , Textos de posgrado en matemáticas, vol. 60 (2.ª ed.), Nueva York: Springer-Verlag, ISBN 978-0-387-90314-9; traducido del ruso por K. Vogtmann y A. Weinstein.
• Berger, Marcel (2004), Una visión panorámica de la geometría de Riemann , Springer-Verlag, ISBN 978-3-540-65317-2
• Berger, Melvyn S. (1977), No linealidad y análisis funcional , Academic Press, ISBN 978-0-12-090350-4
• Bonola, Roberto; Carslaw, HS; Enriques, F. (1955), Geometría no euclidiana: un estudio crítico e histórico de su desarrollo , Dover, ISBN 978-0-486-60027-7
• Boothby, William M. (1986), Introducción a las variedades diferenciables y a la geometría de Riemann , Pure and Applied Mathematics, vol. 120 (2.ª ed.), Academic Press, ISBN 0121160521
• Cartan, Élie (1983), Geometría de los espacios de Riemann, Math Sci Press, ISBN 978-0-915692-34-7; traducido de la segunda edición de Leçons sur la géométrie des espaces de Riemann (1951) de James Glazebrook.
• Cartan, Élie (2001), Geometría de Riemann en un marco ortogonal (de las conferencias dictadas por É Cartan en la Sorbona en 1926-27), World Scientific, ISBN 978-981-02-4746-1; traducido del ruso por VV Goldberg con prólogo de SS Chern .
• Cartan, Henri (1971), Calcul Differentiel (en francés), Hermann , ISBN 9780395120330
• Chen, Xiuxiong; Lu, Peng; Tian, ​​Gang (2006), "Una nota sobre la uniformización de superficies de Riemann mediante flujo de Ricci", Proc. AMS , 134 (11): 3391–3393, doi : 10.1090/S0002-9939-06-08360-2
• Chern, SS (1967), Curvas y superficies en espacios euclidianos , MAA Studies in Mathematics, Asociación Matemática de América
• Chow, B. (1991), "El flujo de Ricci en una esfera de dos dimensiones", J. Diff. Geom. , 33 (2): 325–334, doi : 10.4310/jdg/1214446319
• Courant, Richard (1950), Principio de Dirichlet, mapeo conforme y superficies mínimas , John Wiley & Sons, ISBN 978-0-486-44552-6
• Darboux, Gaston , Lecciones sobre la teoría general de las superficies , Gauthier-VillarsVolumen I (1887), Volumen II (1915) [1889], Volumen III (1894), Volumen IV (1896).
• Ding, W. (2001), "Una prueba del teorema de uniformización en S ² ", J. Partial Differential Equations , 14 : 247–250
• do Carmo, Manfredo P. (2016), Geometría diferencial de curvas y superficies (revisada y actualizada 2.ª ed.), Mineola, NY: Dover Publications, Inc., ISBN 978-0-486-80699-0
• do Carmo, Manfredo (1992), Geometría de Riemann , Matemáticas: teoría y aplicaciones, Birkhäuser, ISBN 0-8176-3490-8
• Eisenhart, Luther Pfahler (2004), Tratado sobre la geometría diferencial de curvas y superficies (reimpresión de la edición de 1909), Dover Publications, Inc., ISBN 0-486-43820-1
• Euler, Leonhard (1760), "Recherches sur la courbure des Surfaces", Mémoires de l'Académie des Sciences de Berlin , 16 (publicado en 1767): 119-143.
• Euler, Leonhard (1771), "De solidis quorum superficiem in planum explicare licet", Novi Commentarii Academiae Scientiarum Petropolitanae , 16 (publicado en 1772): 3–34.
• Gauss, Carl Friedrich (1902), Investigaciones generales sobre superficies curvas de 1825 y 1827, Biblioteca de la Universidad de Princetontraducido por AM Hiltebeitel y JC Morehead; "Disquisitiones generales circa superficies curvas", Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores vol. VI (1827), págs. 99-146.
  • Gauss, Carl Friedrich (1965), Investigaciones generales de superficies curvas , traducido por AM Hiltebeitel; JC Morehead, Hewlett, NY: Raven Press, OCLC  228665499.
  • Gauss, Carl Friedrich (2005), Investigaciones generales de superficies curvas , editado con una nueva introducción y notas de Peter Pesic, Mineola, NY: Dover Publications, ISBN 978-0-486-44645-5.
• Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Geometría diferencial moderna de curvas y superficies con Mathematica® , Estudios en matemáticas avanzadas (3.ª ed.), Boca Raton, FL: Chapman & Hall/CRC, ISBN 978-1-58488-448-4
• Han, Qing; Hong, Jia-Xing (2006), Incrustación isométrica de variedades de Riemann en espacios euclidianos , American Mathematical Society, ISBN 978-0-8218-4071-9
• Helgason, Sigurdur (1978), Geometría diferencial, grupos de Lie y espacios simétricos , Academic Press, Nueva York, ISBN 978-0-12-338460-7
• Hilbert, David ; Cohn-Vossen, Stephan (1952), Geometría y la imaginación (2.ª ed.), Nueva York: Chelsea, ISBN 978-0-8284-1087-8
• Hitchin, Nigel (2013), Geometría de superficies (PDF)
• Hopf, Heinz (1989), Lecciones de geometría diferencial en las grandes universidades , Apuntes de clases de matemáticas, vol. 1000, Springer-Verlag, ISBN 978-3-540-51497-8
• Imayoshi, Y.; Taniguchi, M. (1992), Introducción a los espacios de Techmüller , Springer-Verlag, ISBN 978-0-387-70088-5
• Ivey, Thomas A.; Landsberg, JM (2003), Cartan para principiantes: geometría diferencial a través de marcos móviles y sistemas exteriores , Estudios de posgrado en matemáticas, vol. 61, American Mathematical Society, ISBN 978-0-8218-3375-9
• Katz, Mikhail G. (2007), Geometría sistólica y topología , Mathematical Surveys and Monographs, vol. 137, American Mathematical Society, ISBN 978-0-8218-4177-8
• Milnor, J. (1963). Teoría de Morse . Anales de estudios matemáticos. Vol. 51. Princeton, NJ: Princeton University Press. MR  0163331. Zbl  0108.10401.
• Kobayashi, Shoshichi (1956), "Conexiones inducidas y espacio riemanniano incorporado", Nagoya Math. J. , 10 : 15–25, doi : 10.1017/S0027763000000052
• Kobayashi, Shoshichi (1957), "Teoría de las conexiones", Annali di Matematica Pura ed Applicata , Serie 4, 43 : 119–194, doi : 10.1007/BF02411907 , S2CID  120972987,
• Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Fundamentos de la geometría diferencial, vol. Yo , Wiley Interscience, ISBN 978-0-470-49648-0
• Kobayashi, Shoshichi; Nomizu, Katsumi (1969), Fundamentos de la geometría diferencial, vol. II , Wiley Interscience, ISBN 978-0-470-49648-0
• Kreyszig, Erwin (1991), Geometría diferencial , Dover, ISBN 978-0-486-66721-8
• Kühnel, Wolfgang (2006), Geometría diferencial: curvas, superficies y variedades , American Mathematical Society, ISBN 978-0-8218-3988-1
• Levi-Civita, Tullio (1917), "Nozione di paralelismo in una varietà qualunque", Rend. Circo. Estera. Palermo , 42 : 173–205, doi : 10.1007/BF03014898, S2CID  122088291
• O'Neill, Barrett (2006), Geometría diferencial elemental (2.ª edición revisada), Ámsterdam: Elsevier/Academic Press, ISBN 0-12-088735-5
• Osgood, B.; Phillips, R.; Sarnak, P. (1988), "Extremos de determinantes de laplacianos", J. Funct. Anal. , 80 : 148–211, doi : 10.1016/0022-1236(88)90070-5
• Osserman, Robert (2002), Un estudio de superficies mínimas , Dover, ISBN 978-0-486-49514-9
• Ian R. Porteous (2001) Diferenciación geométrica: para la inteligencia de curvas y superficies , Cambridge University Press ISBN 0-521-00264-8 . 
• Pressley, Andrew (2001), Geometría diferencial elemental , Springer Undergraduate Mathematics Series, Springer-Verlag, ISBN 978-1-85233-152-8
• Sacks, J.; Uhlenbeck, Karen (1981), "La existencia de inmersiones mínimas de 2-esferas", Ann. of Math. , 112 (1): 1–24, doi :10.2307/1971131, JSTOR  1971131
• Singer, Isadore M.; Thorpe, John A. (1967), Apuntes de clase sobre topología y geometría elementales , Springer-Verlag, ISBN 978-0-387-90202-9
• Spivak, Michael (1965), Cálculo en variedades. Un enfoque moderno de los teoremas clásicos del cálculo avanzado , WA Benjamin
• Stillwell, John (1996), Fuentes de geometría hiperbólica , American Mathematical Society, ISBN 978-0-8218-0558-9
• Struik, Dirk (1987), Una historia concisa de las matemáticas (4.ª ed.), Dover Publications, ISBN 0486602559
• Struik, Dirk J. (1988) [1961], Lectures on Classical Differential Geometry (reimpresión de la 2.ª ed.), Nueva York: Dover Publications, Inc., ISBN 0-486-65609-8
• Taylor, Michael E. (1996a), Ecuaciones diferenciales parciales II: estudios cualitativos de ecuaciones lineales , Springer-Verlag, ISBN 978-1-4419-7051-0
• Taylor, Michael E. (1996b), Ecuaciones diferenciales parciales III: ecuaciones no lineales , Springer-Verlag, ISBN 978-1-4419-7048-0
• Thorpe, John A. (1994), Temas elementales de geometría diferencial , Textos de pregrado en matemáticas, Springer-Verlag, ISBN 0387903577
• Toponogov, Victor A. (2005), Geometría diferencial de curvas y superficies: una guía concisa , Springer-Verlag, ISBN 978-0-8176-4384-3
• Valiron, Georges (1986), La geometría diferencial clásica de curvas y superficies , Math Sci Press, ISBN 978-0-915692-39-2Texto completo del libro
• Warner, Frank W. (1983), Fundamentos de variedades diferenciables y grupos de Lie , Textos de posgrado en matemáticas, vol. 94, Springer, ISBN 0-387-90894-3
• Wells, RO (2017), Geometría diferencial y compleja: orígenes, abstracciones e incrustaciones , Springer, ISBN 9783319581842
• Wilson, Pelham (2008), Espacio curvo: de las geometrías clásicas a la geometría diferencial elemental , Cambridge University Press, ISBN 978-0-521-71390-0

Enlaces externos

• Medios relacionados con Geometría diferencial de superficies en Wikimedia Commons