Un número binario es un número expresado en el sistema de numeración de base -2 o sistema de numeración binario , un método para representar números que utiliza solo dos símbolos para los números naturales : típicamente "0" ( cero ) y "1" ( uno ). Un número binario también puede referirse a un número racional que tiene una representación finita en el sistema de numeración binario, es decir, el cociente de un entero por una potencia de dos.
El sistema de numeración de base 2 es una notación posicional con un radio de 2. Cada dígito se denomina bit o dígito binario. Debido a su implementación sencilla en circuitos electrónicos digitales mediante puertas lógicas , el sistema binario es utilizado por casi todos los ordenadores y dispositivos informáticos modernos como sistema de uso preferido, por sobre otras técnicas de comunicación humana, debido a la simplicidad del lenguaje y la inmunidad al ruido en la implementación física. [1]
El sistema de numeración binario moderno fue estudiado en Europa en los siglos XVI y XVII por Thomas Harriot , Juan Caramuel y Lobkowitz y Gottfried Leibniz . Sin embargo, sistemas relacionados con los números binarios han aparecido antes en múltiples culturas, entre ellas el antiguo Egipto, China y la India.
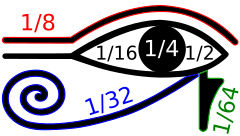
Los escribas del antiguo Egipto utilizaban dos sistemas diferentes para sus fracciones, las fracciones egipcias (no relacionadas con el sistema numérico binario) y las fracciones Ojo de Horus (llamadas así porque muchos historiadores de las matemáticas creen que los símbolos utilizados para este sistema podrían organizarse para formar el ojo de Horus , aunque esto ha sido discutido). [2] Las fracciones Ojo de Horus son un sistema de numeración binario para cantidades fraccionarias de grano, líquidos u otras medidas, en el que una fracción de un hekat se expresa como una suma de las fracciones binarias 1/2, 1/4, 1/8, 1/16, 1/32 y 1/64. Las primeras formas de este sistema se pueden encontrar en documentos de la Quinta Dinastía de Egipto , aproximadamente 2400 a. C., y su forma jeroglífica completamente desarrollada data de la Decimonovena Dinastía de Egipto , aproximadamente 1200 a. C. [3]
El método utilizado para la multiplicación del antiguo Egipto también está estrechamente relacionado con los números binarios. En este método, la multiplicación de un número por un segundo se realiza mediante una secuencia de pasos en los que un valor (inicialmente el primero de los dos números) se duplica o se le vuelve a sumar el primer número; el orden en el que se deben realizar estos pasos viene dado por la representación binaria del segundo número. Este método se puede ver en uso, por ejemplo, en el Papiro matemático de Rhind , que data de alrededor de 1650 a. C. [4]

El I Ching data del siglo IX a. C. en China. [5] La notación binaria en el I Ching se utiliza para interpretar su técnica de adivinación cuaternaria . [6]
Se basa en la dualidad taoísta del yin y el yang . [7] Ocho trigramas (Bagua) y un conjunto de 64 hexagramas ("sesenta y cuatro" gua) , análogos a los numerales binarios de tres y seis bits, se utilizaban al menos desde la dinastía Zhou de la antigua China. [5]
El erudito de la dinastía Song Shao Yong (1011-1077) reorganizó los hexagramas en un formato que se asemeja a los números binarios modernos, aunque no tenía la intención de que su disposición se usara matemáticamente. [6] Viendo el bit menos significativo en la parte superior de los hexagramas individuales en el cuadrado de Shao Yong [8] y leyendo a lo largo de las filas, ya sea de abajo a la derecha a arriba a la izquierda con líneas sólidas como 0 y líneas discontinuas como 1 o de arriba a la izquierda a abajo a la derecha con líneas sólidas como 1 y líneas discontinuas como 0, los hexagramas pueden interpretarse como una secuencia de 0 a 63. [9]
Los etruscos dividían el borde exterior de los hígados adivinatorios en dieciséis partes, cada una de las cuales llevaba inscrito el nombre de una divinidad y su región del cielo. Cada región del hígado producía una lectura binaria que se combinaba en un binario final para la adivinación. [10]
La adivinación en el antiguo oráculo griego de Dodona se basaba en extraer información de frascos separados, tablillas de preguntas y píldoras de "sí" y "no". El resultado se combinaba luego para elaborar una profecía final. [11]
El erudito indio Pingala (c. siglo II a. C.) desarrolló un sistema binario para describir la prosodia . [12] [13] Describió los metros en forma de sílabas cortas y largas (estas últimas con una longitud igual a dos sílabas cortas). [14] Se las conocía como sílabas laghu (ligeras) y guru (pesadas).
El clásico hindú de Pingala titulado Chandaḥśāstra (8.23) describe la formación de una matriz para dar un valor único a cada metro. "Chandaḥśāstra" se traduce literalmente como ciencia de los metros en sánscrito. Las representaciones binarias en el sistema de Pingala aumentan hacia la derecha, y no hacia la izquierda como en los números binarios de la notación posicional moderna . [15] En el sistema de Pingala, los números comienzan desde el número uno, y no desde el cero. Cuatro sílabas cortas "0000" es el primer patrón y corresponde al valor uno. El valor numérico se obtiene sumando uno a la suma de los valores posicionales . [16]
El Ifá es un sistema de adivinación africano . Similar al I Ching , pero tiene hasta 256 signos binarios, [17] a diferencia del I Ching que tiene 64. El Ifá se originó en el siglo XV en África Occidental entre el pueblo yoruba . En 2008, la UNESCO agregó al Ifá a su lista de las " Obras Maestras del Patrimonio Oral e Inmaterial de la Humanidad ". [18] [19]
Los habitantes de la isla de Mangareva en la Polinesia Francesa utilizaban un sistema binario- decimal híbrido antes de 1450. [20] Los tambores de hendidura con tonos binarios se utilizan para codificar mensajes en África y Asia. [7] Los conjuntos de combinaciones binarias similares al I Ching también se han utilizado en los sistemas tradicionales de adivinación africanos, como Ifá entre otros, así como en la geomancia occidental medieval . La mayoría de las lenguas indígenas australianas utilizan un sistema de base 2. [21]
A finales del siglo XIII, Ramon Llull tuvo la ambición de dar cuenta de toda la sabiduría en todas las ramas del conocimiento humano de la época. Para ello desarrolló un método general o “Ars generalis” basado en combinaciones binarias de una serie de principios básicos o categorías simples, por lo que se le ha considerado un precursor de la informática y de la inteligencia artificial. [22]
En 1605, Francis Bacon discutió un sistema por el cual las letras del alfabeto podrían ser reducidas a secuencias de dígitos binarios, que luego podrían ser codificados como variaciones apenas visibles en la fuente en cualquier texto aleatorio. [23] De manera importante para la teoría general de la codificación binaria, agregó que este método podría ser utilizado con cualquier objeto: "siempre que esos objetos sean capaces de una diferencia doble solamente; por ejemplo, por campanas, trompetas, luces y antorchas, por el sonido de los mosquetes y cualquier instrumento de naturaleza similar". [23] (Véase el cifrado de Bacon ).
En 1617, John Napier describió un sistema al que llamó aritmética de localización para realizar cálculos binarios utilizando una representación no posicional mediante letras. Thomas Harriot investigó varios sistemas de numeración posicional, incluido el binario, pero no publicó sus resultados; se encontraron más tarde entre sus artículos. [24] Posiblemente la primera publicación del sistema en Europa fue la de Juan Caramuel y Lobkowitz , en 1700. [25]

Leibniz escribió más de cien manuscritos sobre el sistema binario, la mayoría de los cuales permanecen inéditos. [26] Antes de su primera obra dedicada a él en 1679, numerosos manuscritos presentan intentos tempranos de explorar conceptos binarios, incluyendo tablas de números y cálculos básicos, a menudo garabateados en los márgenes de obras no relacionadas con las matemáticas. [26]
En su primer trabajo conocido sobre el sistema binario, “Sobre la progresión binaria” , de 1679, Leibniz introdujo la conversión entre el sistema decimal y el binario, junto con algoritmos para realizar operaciones aritméticas básicas como la suma, la resta, la multiplicación y la división utilizando números binarios. También desarrolló una forma de álgebra binaria para calcular el cuadrado de un número de seis dígitos y extraer raíces cuadradas. [26]
Su obra más conocida aparece en su artículo Explication de l'Arithmétique Binaire (publicado en 1703). El título completo del artículo de Leibniz se traduce al inglés como "Explication of Binary Arithmetic, which uses only the 1 and 0, with some remarks on its utility, and on the light that it arroja on the ancient Chinese figures of Fu Xi" (Explicación de la aritmética binaria, que utiliza sólo los caracteres 1 y 0, con algunas observaciones sobre su utilidad y sobre la luz que arroja sobre las antiguas cifras chinas de Fu Xi ) . [27] El sistema de Leibniz utiliza 0 y 1, como el sistema de numeración binario moderno. Un ejemplo del sistema de numeración binario de Leibniz es el siguiente: [27]
En 1700, durante una correspondencia con el sacerdote jesuita Joachim Bouvet , que se había convertido en un experto en el I Ching durante su misión en China, Leibniz explicó su notación binaria y Bouvet demostró en sus cartas de 1701 que el I Ching era una invención paralela e independiente de la notación binaria. Leibniz y Bouvet concluyeron que esta correspondencia era una prueba de los importantes logros chinos en el tipo de matemática filosófica que él admiraba. [28] Sobre esta invención paralela, Leibniz escribió en su "Explicación de la aritmética binaria" que "esta restitución de su significado, después de un intervalo de tiempo tan grande, parecerá aún más curiosa". [29]
La relación era una idea central de su concepto universal de lenguaje o characterizati universalis , una idea popular que sería seguida de cerca por sus sucesores como Gottlob Frege y George Boole en la formación de la lógica simbólica moderna . [30] Leibniz conoció por primera vez el I Ching a través de su contacto con el jesuita francés Joachim Bouvet , quien visitó China en 1685 como misionero. Leibniz vio los hexagramas del I Ching como una afirmación de la universalidad de sus propias creencias religiosas como cristiano. [31] Los números binarios fueron centrales para la teología de Leibniz. Creía que los números binarios eran simbólicos de la idea cristiana de creatio ex nihilo o creación de la nada. [32]
[Un concepto que] no es fácil de transmitir a los paganos es el de la creación ex nihilo por medio del poder omnipotente de Dios. Ahora bien, se puede decir que nada en el mundo puede presentar y demostrar mejor este poder que el origen de los números, tal como se presenta aquí a través de la presentación simple y sin adornos del Uno y el Cero o la Nada.
— Carta de Leibniz al duque de Brunswick adjunta con los hexagramas del I Ching [31]

En 1854, el matemático británico George Boole publicó un artículo fundamental en el que detallaba un sistema algebraico de lógica que se conocería como álgebra de Boole . Su cálculo lógico sería fundamental para el diseño de circuitos electrónicos digitales. [33]
En 1937, Claude Shannon elaboró su tesis de maestría en el MIT , en la que implementó el álgebra de Boole y la aritmética binaria utilizando relés e interruptores electrónicos por primera vez en la historia. Titulada Un análisis simbólico de los circuitos de conmutación y relés , la tesis de Shannon esencialmente sentó las bases del diseño práctico de circuitos digitales . [34]
En noviembre de 1937, George Stibitz , que trabajaba en los Laboratorios Bell , completó una computadora basada en relés que denominó "Modelo K" (por " K itchen", donde la había ensamblado), que calculaba mediante la adición binaria. [35] Los Laboratorios Bell autorizaron un programa de investigación completo a fines de 1938 con Stibitz al mando. Su Computadora de Números Complejos, completada el 8 de enero de 1940, pudo calcular números complejos . En una demostración en la conferencia de la Sociedad Matemática Estadounidense en el Dartmouth College el 11 de septiembre de 1940, Stibitz pudo enviar comandos remotos a la Calculadora de Números Complejos a través de líneas telefónicas mediante un teletipo . Fue la primera máquina de computación jamás utilizada de forma remota a través de una línea telefónica. Algunos participantes de la conferencia que presenciaron la demostración fueron John von Neumann , John Mauchly y Norbert Wiener , quien escribió sobre ella en sus memorias. [36] [37] [38]
La computadora Z1 , que fue diseñada y construida por Konrad Zuse entre 1935 y 1938, utilizaba lógica booleana y números binarios de punto flotante . [39]
Cualquier número puede representarse mediante una secuencia de bits (dígitos binarios), que a su vez pueden representarse mediante cualquier mecanismo capaz de estar en dos estados mutuamente excluyentes. Cualquiera de las siguientes filas de símbolos puede interpretarse como el valor numérico binario de 667:

El valor numérico representado en cada caso depende del valor asignado a cada símbolo. En los primeros tiempos de la informática, se utilizaban interruptores, agujeros perforados y cintas de papel perforadas para representar valores binarios. [40] En una computadora moderna, los valores numéricos pueden representarse mediante dos voltajes diferentes ; en un disco magnético , se pueden utilizar polaridades magnéticas . Un estado "positivo", " sí " o "encendido" no es necesariamente equivalente al valor numérico de uno; depende de la arquitectura en uso.
De acuerdo con la representación habitual de los números mediante números arábigos , los números binarios se escriben comúnmente con los símbolos 0 y 1. Cuando se escriben, los números binarios suelen ir acompañados de subíndices, prefijos o sufijos para indicar su base o radix . Las siguientes notaciones son equivalentes:
Cuando se pronuncian, los números binarios se suelen leer dígito por dígito, para distinguirlos de los números decimales. Por ejemplo, el número binario 100 se pronuncia uno cero cero , en lugar de cien , para hacer explícita su naturaleza binaria y con fines de corrección. Dado que el número binario 100 representa el valor cuatro, sería confuso referirse al número como cien (una palabra que representa un valor o cantidad completamente diferente). Alternativamente, el número binario 100 se puede leer como "cuatro" (el valor correcto ), pero esto no hace explícita su naturaleza binaria.
El conteo en binario es similar al conteo en cualquier otro sistema numérico. Se comienza con un solo dígito y se procede a contar con cada símbolo en orden creciente. Antes de analizar el conteo binario, es útil analizar brevemente el sistema de conteo decimal, más conocido , como marco de referencia.
El conteo decimal utiliza los diez símbolos del 0 al 9. El conteo comienza con la sustitución incremental del dígito menos significativo (dígito más a la derecha), que a menudo se denomina primer dígito . Cuando se agotan los símbolos disponibles para esta posición, el dígito menos significativo se restablece a 0 y el siguiente dígito de mayor importancia (una posición a la izquierda) se incrementa ( desbordamiento ), y se reanuda la sustitución incremental del dígito de orden inferior. Este método de restablecimiento y desbordamiento se repite para cada dígito de importancia. El conteo avanza de la siguiente manera:

El conteo binario sigue exactamente el mismo procedimiento y, nuevamente, la sustitución incremental comienza con el dígito binario menos significativo, o bit (el que está más a la derecha, también llamado primer bit ), excepto que solo están disponibles los dos símbolos 0 y 1. Por lo tanto, después de que un bit llega a 1 en binario, un incremento lo restablece a 0 pero también provoca un incremento del siguiente bit a la izquierda:
En el sistema binario, cada bit representa una potencia creciente de 2, donde el bit más a la derecha representa 2 0 , el siguiente representa 2 1 , luego 2 2 , y así sucesivamente. El valor de un número binario es la suma de las potencias de 2 representadas por cada bit "1". Por ejemplo, el número binario 100101 se convierte a formato decimal de la siguiente manera:
Las fracciones en aritmética binaria terminan solo si el denominador es una potencia de 2. Como resultado, 1/10 no tiene una representación binaria finita ( 10 tiene factores primos 2 y 5 ). Esto hace que 10 × 1/10 no sea exactamente igual a 1 en aritmética binaria de punto flotante . Como ejemplo, para interpretar la expresión binaria para 1/3 = .010101..., esto significa: 1/3 = 0 × 2 −1 + 1 × 2 −2 + 0 × 2 −3 + 1 × 2 −4 + ... = 0.3125 + ... No se puede encontrar un valor exacto con una suma de un número finito de potencias inversas de dos, los ceros y unos en la representación binaria de 1/3 se alternan para siempre.
La aritmética en binario es muy parecida a la aritmética en otros sistemas numéricos de notación posicional . Se pueden realizar sumas, restas, multiplicaciones y divisiones en números binarios.
La operación aritmética más sencilla en binario es la suma. Sumar dos números binarios de un solo dígito es relativamente sencillo y se utiliza una forma de llevar:
La suma de dos dígitos "1" produce un dígito "0", mientras que el 1 deberá agregarse a la siguiente columna. Esto es similar a lo que sucede en el sistema decimal cuando se suman ciertos números de un solo dígito; si el resultado es igual o mayor que el valor de la base (10), se incrementa el dígito de la izquierda:
Esto se conoce como llevar . Cuando el resultado de una suma supera el valor de un dígito, el procedimiento es "llevar" la cantidad sobrante dividida por la base (es decir, 10/10) hacia la izquierda, sumándola al siguiente valor posicional. Esto es correcto ya que la siguiente posición tiene un peso que es mayor por un factor igual a la base. El llevar funciona de la misma manera en binario:
1 1 1 1 1 (dígitos transportados) 0 1 1 0 1+ 1 0 1 1 1-------------= 1 0 0 1 0 0 = 36En este ejemplo, se suman dos números: 01101 2 (13 10 ) y 10111 2 (23 10 ). La fila superior muestra los bits de acarreo utilizados. Empezando por la columna más a la derecha, 1 + 1 = 10 2 . El 1 se lleva a la izquierda y el 0 se escribe en la parte inferior de la columna más a la derecha. Se suma la segunda columna desde la derecha: 1 + 0 + 1 = 10 2 de nuevo; se lleva el 1 y se escribe el 0 en la parte inferior. La tercera columna: 1 + 1 + 1 = 11 2 . Esta vez, se lleva un 1 y se escribe un 1 en la fila inferior. Procediendo de esta manera, se obtiene la respuesta final 100100 2 (36 10 ).
Cuando las computadoras deben sumar dos números, la regla: x xor y = (x + y) mod 2 para cualesquiera dos bits x e y también permite un cálculo muy rápido.
Una simplificación para muchos problemas de suma binaria es el "método de acarreo largo" o "método Brookhouse de suma binaria". Este método es particularmente útil cuando uno de los números contiene una larga serie de unos. Se basa en la sencilla premisa de que, en el sistema binario, cuando se da una serie de dígitos compuesta enteramente por n unos (donde n es cualquier longitud entera), sumar 1 dará como resultado el número 1 seguido de una cadena de n ceros. Ese concepto se desprende, lógicamente, del mismo modo que en el sistema decimal, donde sumar 1 a una cadena de n 9 dará como resultado el número 1 seguido de una cadena de n 0:
Decimal binario 1 1 1 1 1 igualmente 9 9 9 9 9 + 1 + 1 ——————————— ——————————— 1 0 0 0 0 0 1 0 0 0 0 0
Este tipo de cadenas largas son bastante comunes en el sistema binario. De ahí que se descubra que se pueden sumar números binarios grandes utilizando dos sencillos pasos, sin operaciones de acarreo excesivas. En el siguiente ejemplo, se suman dos números: 1 1 1 0 1 1 1 1 1 0 2 (958 10 ) y 1 0 1 0 1 1 0 0 1 1 2 (691 10 ), utilizando el método de acarreo tradicional a la izquierda y el método de acarreo largo a la derecha:
Método de transporte tradicional Método de transporte largo vs. 1 1 1 1 1 1 1 1 (dígitos transportados) 1 ← 1 ← transporta el 1 hasta que esté un dígito más allá de la "cadena" de abajo 1 1 1 0 1 1 1 1 1 01 1 101 1 1 1 10 tacha la "cadena",+ 1 0 1 0 1 1 0 0 1 1 + 1 010 1 1 0 011 y tacha el dígito que se le agregó——————————————————————— ———————————————————————= 1 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1
La fila superior muestra los bits de acarreo utilizados. En lugar del acarreo estándar de una columna a la siguiente, se puede agregar el "1" de menor orden con un "1" en el valor de posición correspondiente debajo y se puede llevar un "1" a un dígito más allá del final de la serie. Los números "utilizados" deben eliminarse, ya que ya se han agregado. Otras cadenas largas también se pueden cancelar utilizando la misma técnica. Luego, simplemente se suman los dígitos restantes normalmente. Procediendo de esta manera se obtiene la respuesta final de 1 1 0 0 1 1 1 0 0 0 1 2 (1649 10 ). En nuestro ejemplo simple con números pequeños, el método de acarreo tradicional requirió ocho operaciones de acarreo, mientras que el método de acarreo largo requirió solo dos, lo que representa una reducción sustancial del esfuerzo.
La tabla de adición binaria es similar, pero no igual, a la tabla de verdad de la operación de disyunción lógica . La diferencia es que , mientras que .
La resta funciona de la misma manera:
Restar un dígito "1" de un dígito "0" produce el dígito "1", mientras que habrá que restar 1 de la siguiente columna. Esto se conoce como préstamo . El principio es el mismo que para el acarreo. Cuando el resultado de una resta es menor que 0, el menor valor posible de un dígito, el procedimiento es "tomar prestado" el déficit dividido por la base (es decir, 10/10) de la izquierda, restándolo del siguiente valor posicional.
* * * * (las columnas marcadas con asterisco están tomadas de) 1 1 0 1 1 1 0- 1 0 1 1 1----------------= 1 0 1 0 1 1 1
* (las columnas marcadas con asterisco están tomadas de) 1 0 1 1 1 1 1– 1 0 1 0 1 1----------------= 0 1 1 0 1 0 0
Restar un número positivo es equivalente a sumar un número negativo de igual valor absoluto . Las computadoras utilizan representaciones de números con signo para manejar números negativos, la más común es la notación de complemento a dos . Dichas representaciones eliminan la necesidad de una operación de "resta" separada. Usando la notación de complemento a dos, la resta se puede resumir con la siguiente fórmula:
La multiplicación en binario es similar a su contraparte decimal. Dos números A y B se pueden multiplicar por productos parciales: para cada dígito de B , se calcula el producto de ese dígito en A y se escribe en una nueva línea, desplazada hacia la izquierda de modo que su dígito más a la derecha se alinee con el dígito de B que se utilizó. La suma de todos estos productos parciales da el resultado final.
Como en binario solo hay dos dígitos, solo hay dos resultados posibles de cada multiplicación parcial:
Por ejemplo, los números binarios 1011 y 1010 se multiplican de la siguiente manera:
1 0 1 1 ( Un ) × 1 0 1 0 ( B ) --------- 0 0 0 0 ← Corresponde al 'cero' más a la derecha en B + 1 0 1 1 ← Corresponde al siguiente 'uno' en B + 0 0 0 0 + 1 0 1 1 --------------- = 1 1 0 1 1 1 0
Los números binarios también se pueden multiplicar con bits después de un punto binario :
1 0 1 . 1 0 1 A (5,625 en decimal) × 1 1 0 . 0 1 B (6,25 en decimal) ------------------- 1 . 0 1 1 0 1 ← Corresponde a un 'uno' en B + 0 0 . 0 0 0 0 ← Corresponde a un 'cero' en B + 0 0 0 . 0 0 0 + 1 0 1 1 . 0 1 + 1 0 1 1 0 . 1 --------------------------- = 1 0 0 0 1 1 . 0 0 1 0 1 (35,15625 en decimal)
Véase también el algoritmo de multiplicación de Booth .
La tabla de multiplicación binaria es la misma que la tabla de verdad de la operación de conjunción lógica .
La división larga en binario es nuevamente similar a su contraparte decimal.
En el ejemplo siguiente, el divisor es 101 2 , o 5 en decimal, mientras que el dividendo es 11011 2 , o 27 en decimal. El procedimiento es el mismo que el de la división decimal larga ; aquí, el divisor 101 2 entra en los primeros tres dígitos 110 2 del dividendo una vez, por lo que se escribe un "1" en la línea superior. Este resultado se multiplica por el divisor y se resta de los primeros tres dígitos del dividendo; el siguiente dígito (un "1") se incluye para obtener una nueva secuencia de tres dígitos:
1 ___________1 0 1 ) 1 1 0 1 1 - 1 0 1 ----- 0 0 1
Luego se repite el procedimiento con la nueva secuencia, hasta agotar los dígitos del dividendo:
1 0 1 ___________1 0 1 ) 1 1 0 1 1 - 1 0 1 ----- 1 1 1 - 1 0 1 ----- 0 1 0
Así, el cociente de 11011 2 dividido por 101 2 es 101 2 , como se muestra en la línea superior, mientras que el resto, que se muestra en la línea inferior, es 10 2 . En decimal, esto corresponde al hecho de que 27 dividido por 5 es 5, con un resto de 2.
Además de la división larga, también se puede idear el procedimiento para permitir la resta excesiva del resto parcial en cada iteración, lo que conduce a métodos alternativos que son menos sistemáticos, pero más flexibles como resultado.
El proceso para obtener una raíz cuadrada binaria dígito por dígito es el mismo que para obtener una raíz cuadrada decimal y se explica aquí . Un ejemplo es:
1 0 0 1 --------- √ 1010001 1 --------- 101 01 0 -------- 1001 100 0 -------- 10001 10001 10001 ------- 0
Aunque no están directamente relacionadas con la interpretación numérica de los símbolos binarios, las secuencias de bits pueden manipularse utilizando operadores lógicos booleanos . Cuando una cadena de símbolos binarios se manipula de esta manera, se denomina operación bit a bit ; los operadores lógicos AND , OR y XOR pueden realizarse en bits correspondientes en dos números binarios proporcionados como entrada. La operación lógica NOT puede realizarse en bits individuales en un solo número binario proporcionado como entrada. A veces, estas operaciones pueden usarse como atajos aritméticos y también pueden tener otros beneficios computacionales. Por ejemplo, un desplazamiento aritmético a la izquierda de un número binario es el equivalente a la multiplicación por una potencia (positiva, integral) de 2.
Para convertir un entero de base 10 a su equivalente de base 2 (binario), el número se divide por dos . El resto es el bit menos significativo . El cociente se divide nuevamente por dos; su resto se convierte en el siguiente bit menos significativo. Este proceso se repite hasta que se alcanza un cociente de uno. La secuencia de restos (incluido el cociente final de uno) forma el valor binario, ya que cada resto debe ser cero o uno al dividir por dos. Por ejemplo, (357) 10 se expresa como (101100101) 2. [43]
La conversión de base 2 a base 10 simplemente invierte el algoritmo anterior. Los bits del número binario se utilizan uno por uno, comenzando con el bit más significativo (el más a la izquierda). Comenzando con el valor 0, el valor anterior se duplica y luego se suma el siguiente bit para producir el siguiente valor. Esto se puede organizar en una tabla de varias columnas. Por ejemplo, para convertir 10010101101 2 a decimal:
El resultado es 1197 10. El primer valor anterior de 0 es simplemente un valor decimal inicial. Este método es una aplicación del esquema de Horner .
Las partes fraccionarias de un número se convierten con métodos similares. Nuevamente, se basan en la equivalencia de desplazamiento con duplicación o división a la mitad.
En un número binario fraccionario como 0,11010110101 2 , el primer dígito es , el segundo , etc. Por lo tanto, si hay un 1 en el primer lugar después del decimal, entonces el número es al menos , y viceversa. El doble de ese número es al menos 1. Esto sugiere el algoritmo: duplicar repetidamente el número a convertir, registrar si el resultado es al menos 1 y luego descartar la parte entera.
Por ejemplo, , en binario, es:
Por lo tanto, la fracción decimal periódica 0,3 ... es equivalente a la fracción binaria periódica 0,01 ...
O por ejemplo, 0,1 10 , en binario, es:
Esta es también una fracción binaria periódica 0.0 0011 ... . Puede resultar sorprendente que las fracciones decimales terminales puedan tener expansiones repetidas en binario. Es por esta razón que a muchos les sorprende descubrir que 1/10 + ... + 1/10 (suma de 10 números) difiere de 1 en aritmética binaria de punto flotante . De hecho, las únicas fracciones binarias con expansiones terminales tienen la forma de un entero dividido por una potencia de 2, que no es 1/10.
La conversión final es de fracciones binarias a decimales. La única dificultad surge con las fracciones repetidas, pero de lo contrario el método es convertir la fracción a un entero, convertirla como se indicó anteriormente y luego dividirla por la potencia de dos correspondiente en la base decimal. Por ejemplo:
Otra forma de convertir de binario a decimal, a menudo más rápida para una persona familiarizada con el sistema hexadecimal , es hacerlo indirectamente: primero convirtiendo ( en binario) en ( en hexadecimal) y luego convirtiendo ( en hexadecimal) en ( en decimal).
Para números muy grandes, estos métodos simples son ineficientes porque realizan una gran cantidad de multiplicaciones o divisiones donde un operando es muy grande. Un algoritmo simple de divide y vencerás es más efectivo asintóticamente: dado un número binario, se divide por 10 k , donde k se elige de modo que el cociente sea aproximadamente igual al resto; luego, cada una de estas partes se convierte a decimal y las dos se concatenan . Dado un número decimal, se puede dividir en dos partes de aproximadamente el mismo tamaño, cada una de las cuales se convierte a binario, con lo cual la primera parte convertida se multiplica por 10 k y se suma a la segunda parte convertida, donde k es el número de dígitos decimales en la segunda parte, la menos significativa, antes de la conversión.
El sistema binario se puede convertir a y desde el sistema hexadecimal con mayor facilidad. Esto se debe a que la base del sistema hexadecimal (16) es una potencia de la base del sistema binario (2). Más específicamente, 16 = 2 4 , por lo que se necesitan cuatro dígitos del sistema binario para representar un dígito del sistema hexadecimal, como se muestra en la tabla adyacente.
Para convertir un número hexadecimal en su equivalente binario, simplemente sustituya los dígitos binarios correspondientes:
Para convertir un número binario en su equivalente hexadecimal, divídalo en grupos de cuatro bits. Si la cantidad de bits no es múltiplo de cuatro, simplemente inserte bits 0 adicionales a la izquierda (lo que se denomina relleno ). Por ejemplo:
Para convertir un número hexadecimal en su equivalente decimal, multiplique el equivalente decimal de cada dígito hexadecimal por la potencia de 16 correspondiente y sume los valores resultantes:
El sistema binario también se puede convertir fácilmente al sistema de numeración octal , ya que el octal utiliza una base de 8, que es una potencia de dos (es decir, 2 3 , por lo que se necesitan exactamente tres dígitos binarios para representar un dígito octal). La correspondencia entre los números octales y binarios es la misma que para los primeros ocho dígitos del sistema hexadecimal en la tabla anterior. El binario 000 es equivalente al dígito octal 0, el binario 111 es equivalente al octal 7, y así sucesivamente.
La conversión de octal a binario se realiza de la misma manera que para el hexadecimal :
Y de binario a octal:
Y de octal a decimal:
Los números no enteros se pueden representar mediante potencias negativas, que se separan de los demás dígitos mediante un punto decimal (llamado punto decimal en el sistema decimal). Por ejemplo, el número binario 11.01 2 significa:
Para un total de 3,25 decimales.
Todos los números racionales diádicos tienen un numeral binario terminal : la representación binaria tiene un número finito de términos después del punto de base. Otros números racionales tienen representación binaria, pero en lugar de ser terminales, recurren , con una secuencia finita de dígitos que se repiten indefinidamente. Por ejemplo
El fenómeno de que la representación binaria de cualquier racional sea terminal o recurrente también ocurre en otros sistemas de numeración basados en la base. Véase, por ejemplo, la explicación en decimal . Otra similitud es la existencia de representaciones alternativas para cualquier representación terminal, basándose en el hecho de que 0,111111... es la suma de la serie geométrica 2 −1 + 2 −2 + 2 −3 + ... que es 1.
Los números binarios que no terminan ni se repiten representan números irracionales . Por ejemplo,
Se podría decir que [la secuencia binaria Fuxi] es una forma más sensata de representar el hexagrama como números binarios... Se desconoce el razonamiento, si lo hay, que informa la secuencia [King Wen].