En física de la materia condensada , el término frustración geométrica (o en resumen: frustración [1] ) se refiere a un fenómeno en el que los átomos tienden a adherirse a posiciones no triviales [ cita requerida ] o donde, en una red cristalina regular , se producen conflictos interatómicos. Las fuerzas (cada una de las cuales favorece estructuras bastante simples, pero diferentes) conducen a estructuras bastante complejas. Como consecuencia de la frustración en la geometría o en las fuerzas, puede resultar una plenitud de estados fundamentales distintos a temperatura cero, y el ordenamiento térmico habitual puede suprimirse a temperaturas más altas. Ejemplos muy estudiados son los materiales amorfos , los vidrios o los imanes diluidos .
El término frustración , en el contexto de los sistemas magnéticos , fue introducido por Gerard Toulouse en 1977. [2] [3] Los sistemas magnéticos frustrados habían sido estudiados incluso antes. Los primeros trabajos incluyen un estudio del modelo de Ising en una red triangular con espines vecinos más cercanos acoplados antiferromagnéticamente , realizado por GH Wannier , publicado en 1950. [4] Características relacionadas ocurren en imanes con interacciones competitivas , donde tanto acoplamientos ferromagnéticos como antiferromagnéticos entre Hay pares de espines o momentos magnéticos, dependiendo el tipo de interacción de la distancia de separación de los espines. En ese caso , puede resultar conmensurabilidad , como disposiciones de espín helicoidal , como lo habían discutido originalmente, especialmente, A. Yoshimori, [5] TA Kaplan, [6] RJ Elliott , [7] y otros, a partir de 1959, para describir Hallazgos experimentales sobre metales de tierras raras. Unas dos décadas después, a partir de la década de 1970, surgió un interés renovado en estos sistemas de espín con interacciones frustradas o competitivas, en el contexto de los vidrios de espín y las superestructuras magnéticas espacialmente moduladas. En los vasos giratorios, la frustración aumenta por el desorden estocástico en las interacciones, como puede ocurrir experimentalmente en aleaciones magnéticas no estequiométricas . Los modelos de espín cuidadosamente analizados con frustración incluyen el modelo de Sherrington-Kirkpatrick , [8] que describe vasos de espín, y el modelo ANNNI , [9] que describe superestructuras magnéticas de conmensurabilidad . Recientemente, el concepto de frustración se ha utilizado en el análisis de redes cerebrales para identificar el conjunto no trivial de conexiones neuronales y resaltar los elementos ajustables del cerebro. [10]
La frustración geométrica es una característica importante del magnetismo , donde surge de la disposición relativa de los espines . En la Figura 1 se muestra un ejemplo 2D simple. Tres iones magnéticos residen en las esquinas de un triángulo con interacciones antiferromagnéticas entre ellos; la energía se minimiza cuando cada giro está alineado opuesto a los vecinos. Una vez que los dos primeros giros se alinean en forma antiparalela, el tercero se frustra porque sus dos posibles orientaciones, arriba y abajo, dan la misma energía. El tercer giro no puede minimizar simultáneamente sus interacciones con los otros dos. Dado que este efecto ocurre para cada giro, el estado fundamental está seis veces degenerado . Sólo los dos estados donde todos los giros son hacia arriba o hacia abajo tienen más energía.
De manera similar, en tres dimensiones, cuatro espines dispuestos en un tetraedro (Figura 2) pueden experimentar frustración geométrica. Si existe una interacción antiferromagnética entre espines, entonces no es posible organizar los espines de modo que todas las interacciones entre espines sean antiparalelas. Hay seis interacciones con el vecino más cercano, cuatro de las cuales son antiparalelas y, por tanto, favorables, pero dos de las cuales (entre 1 y 2, y entre 3 y 4) son desfavorables. Es imposible que todas las interacciones sean favorables y el sistema se frustra.
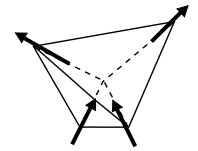
La frustración geométrica también es posible si los espines se disponen de forma no colineal . Si consideramos un tetraedro con un espín en cada vértice apuntando a lo largo del eje fácil (es decir, directamente hacia o lejos del centro del tetraedro), entonces es posible organizar los cuatro espines de manera que no haya espín neto (Figura 3). Esto es exactamente equivalente a tener una interacción antiferromagnética entre cada par de espines, por lo que en este caso no hay frustración geométrica. Con estos ejes, surge una frustración geométrica si hay una interacción ferromagnética entre vecinos, donde la energía se minimiza mediante espines paralelos. La mejor disposición posible se muestra en la Figura 4, con dos giros apuntando hacia el centro y dos apuntando hacia afuera. El momento magnético neto apunta hacia arriba, maximizando las interacciones ferromagnéticas en esta dirección, pero los vectores izquierdo y derecho se cancelan (es decir, están antiferromagnéticamente alineados), al igual que hacia adelante y hacia atrás. Hay tres disposiciones equivalentes diferentes con dos espines hacia afuera y dos hacia adentro, por lo que el estado fundamental es tres veces degenerado.
La definición matemática es simple (y análoga al llamado bucle de Wilson en cromodinámica cuántica ): se consideran, por ejemplo, expresiones ("energías totales" o "hamiltonianas") de la forma
donde G es el gráfico considerado, mientras que las cantidades I k ν , k μ son las llamadas "energías de intercambio" entre vecinos más cercanos, que (en las unidades de energía consideradas) asumen los valores ±1 (matemáticamente, esto es un gráfico con signo gráfico ), mientras que los S k ν · S k μ son productos internos de espines o pseudoespines escalares o vectoriales. Si el gráfico G tiene caras cuadráticas o triangulares P , aparecen las llamadas "variables de placa" P W , "productos de bucle" del siguiente tipo:
que también se denominan "productos de frustración". Hay que realizar una suma sobre estos productos, sumando todas las plaquetas. El resultado para una sola plaqueta es +1 o −1. En este último caso la plaqueta está "geométricamente frustrada".
Se puede demostrar que el resultado tiene una invariancia de calibre simple : no cambia –ni tampoco otras cantidades mensurables, por ejemplo la "energía total" - incluso si localmente las integrales de intercambio y los espines se modifican simultáneamente de la siguiente manera:
Aquí los números ε i y ε k son signos arbitrarios, es decir, +1 o −1, de modo que la estructura modificada puede parecer totalmente aleatoria.
Aunque la mayoría de las investigaciones anteriores y actuales sobre la frustración se centran en los sistemas de espín, el fenómeno se estudió por primera vez en hielo ordinario . En 1936 Giauque y Stout publicaron La entropía del agua y la tercera ley de la termodinámica. Capacidad calorífica del hielo de 15 K a 273 K , reportando mediciones calorimétricas del agua a través de las transiciones de congelación y vaporización hasta la fase gaseosa de alta temperatura. La entropía se calculó integrando la capacidad calorífica y sumando las contribuciones de calor latente ; las mediciones de baja temperatura se extrapolaron a cero, utilizando la fórmula recientemente derivada de Debye. [11] La entropía resultante, S 1 = 44,28 cal/(K·mol) = 185,3 J/(mol·K) se comparó con el resultado teórico de la mecánica estadística de un gas ideal, S 2 = 45,10 cal/(K· mol) = 188,7 J/(mol·K). Los dos valores difieren en S 0 = 0,82 ± 0,05 cal/(K·mol) = 3,4 J/(mol·K). Este resultado fue luego explicado por Linus Pauling [12] con una excelente aproximación, quien demostró que el hielo posee una entropía finita (estimada en 0,81 cal/(K·mol) o 3,4 J/(mol·K)) a temperatura cero debido a el desorden configuracional intrínseco a los protones en el hielo.
En la fase de hielo hexagonal o cúbica , los iones de oxígeno forman una estructura tetraédrica con una longitud de enlace O – O de 2,76 Å (276 pm ), mientras que la longitud del enlace O – H mide sólo 0,96 Å (96 pm). Cada ion de oxígeno (blanco) está rodeado por cuatro iones de hidrógeno (negro) y cada ion de hidrógeno está rodeado por 2 iones de oxígeno, como se muestra en la Figura 5. Manteniendo la estructura interna de la molécula de H 2 O, la posición de energía mínima de un protón no es a medio camino entre dos iones de oxígeno adyacentes. Hay dos posiciones equivalentes que puede ocupar un hidrógeno en la línea del enlace O-O, una posición lejana y otra cercana. Así, una regla conduce a la frustración de las posiciones del protón para una configuración del estado fundamental: por cada oxígeno, dos de los protones vecinos deben estar en la posición lejana y dos de ellos en la posición cercana, las llamadas " reglas de hielo ". Pauling propuso que la estructura tetraédrica abierta del hielo ofrece muchos estados equivalentes que satisfacen las reglas del hielo.
Pauling pasó a calcular la entropía configuracional de la siguiente manera: considere un mol de hielo, que consta de N O 2− y 2 N protones. Cada enlace O–O tiene dos posiciones para un protón, lo que da lugar a 2 2 N configuraciones posibles. Sin embargo, entre las 16 configuraciones posibles asociadas con cada oxígeno, sólo 6 son energéticamente favorables, manteniendo la restricción de la molécula de H 2 O. Entonces, un límite superior de los números que puede tomar el estado fundamental se estima como Ω < 2 2 N (6/dieciséis) norte . En consecuencia, la entropía configuracional S 0 = k B ln( Ω ) = Nk B ln(3/2) = 0,81 cal/(K·mol) = 3,4 J/(mol·K) concuerda sorprendentemente con la entropía faltante medida por Giauque y Stout.
Aunque el cálculo de Pauling descuidó tanto la restricción global sobre el número de protones como la restricción local que surge de los bucles cerrados en la red de Wurtzita, posteriormente se demostró que la estimación tenía una precisión excelente.
Una situación matemáticamente análoga a la degeneración del hielo de agua se encuentra en los hielos de espín . En la Figura 6 se muestra una estructura de hielo de espín común en la estructura de pirocloro cúbico con un átomo o ion magnético residiendo en cada una de las cuatro esquinas. Debido al fuerte campo cristalino en el material, cada uno de los iones magnéticos puede representarse mediante un doblete del estado fundamental de Ising con un gran momento. Esto sugiere una imagen de espines de Ising que residen en la red tetraédrica que comparte esquinas con espines fijados a lo largo del eje de cuantificación local, los <111> ejes cúbicos , que coinciden con las líneas que conectan cada vértice tetraédrico con el centro. Cada celda tetraédrica debe tener dos espines apuntando hacia adentro y dos hacia afuera para minimizar la energía. Actualmente, el modelo de hielo giratorio se ha realizado aproximadamente con materiales reales, en particular los pirocloros de tierras raras Ho 2 Ti 2 O 7 , Dy 2 Ti 2 O 7 y Ho2Sn2O7. Todos estos materiales muestran una entropía residual distinta de cero a baja temperatura.
El modelo de hielo giratorio es sólo una subdivisión de los sistemas frustrados. La palabra frustración se introdujo inicialmente para describir la incapacidad de un sistema para minimizar simultáneamente la energía de interacción competitiva entre sus componentes. En general, la frustración es causada por interacciones competitivas debido al desorden del sitio (ver también el modelo del villano [13] ) o por una estructura reticular como la triangular , la cúbica centrada en las caras (fcc), la hexagonal compacta , el tetraedro , el pirocloro. y celosías kagome con interacción antiferromagnética. Así, la frustración se divide en dos categorías: la primera corresponde al vaso giratorio , que tiene a la vez desorden en la estructura y frustración en el giro; el segundo es la frustración geométrica con una estructura reticular ordenada y la frustración del espín. La frustración de un vidrio giratorio se entiende en el marco del modelo RKKY , en el que la propiedad de interacción, ya sea ferromagnética o antiferromagnética, depende de la distancia de los dos iones magnéticos. Debido al desorden de la red en el vidrio de espín, un espín de interés y sus vecinos más cercanos podrían estar a diferentes distancias y tener una propiedad de interacción diferente, lo que conduce a una alineación preferida diferente del espín.
Con la ayuda de técnicas de litografía, es posible fabricar islas magnéticas de tamaño submicrométrico cuya disposición geométrica reproduce la frustración que se encuentra en los materiales de hielo espín naturales. Recientemente RF Wang et al. informó [14] el descubrimiento de un imán artificial frustrado geométricamente compuesto de conjuntos de islas ferromagnéticas de dominio único fabricadas litográficamente. Estas islas están dispuestas manualmente para crear un análogo bidimensional para hacer girar el hielo. Se tomaron imágenes de los momentos magnéticos de las islas de "espín" ordenadas con microscopía de fuerza magnética (MFM) y luego se estudió en profundidad la acomodación local de la frustración. En su trabajo anterior sobre una red cuadrada de imanes frustrados, observaron tanto correlaciones de corto alcance similares al hielo como la ausencia de correlaciones de largo alcance, al igual que en el hielo giratorio a baja temperatura. Estos resultados solidifican el terreno inexplorado en el que se puede visualizar y modelar la física real de la frustración mediante estos imanes artificiales frustrados geométricamente, e inspiran futuras actividades de investigación.
Estos ferroimanes frustrados artificialmente pueden exhibir propiedades magnéticas únicas al estudiar su respuesta global a un campo externo utilizando el efecto Kerr magnetoóptico. [15] En particular, se encuentra que una dependencia angular no monótona de la coercitividad de la red cuadrada está relacionada con el desorden en el sistema de hielo artificial.
Otro tipo de frustración geométrica surge de la propagación de un orden local. Una de las principales cuestiones a las que se enfrenta un físico de la materia condensada es explicar la estabilidad de un sólido.
En ocasiones es posible establecer algunas reglas locales, de naturaleza química, que conducen a configuraciones de baja energía y por tanto rigen el orden estructural y químico. Generalmente este no es el caso y, a menudo, el orden local definido por las interacciones locales no puede propagarse libremente, lo que lleva a una frustración geométrica. Una característica común de todos estos sistemas es que, incluso con reglas locales simples, presentan un gran conjunto de realizaciones estructurales, a menudo complejas. La frustración geométrica juega un papel en campos de materia condensada, que van desde cúmulos y sólidos amorfos hasta fluidos complejos.
El método general de abordaje para resolver estas complicaciones sigue dos pasos. En primer lugar, la restricción del llenado perfecto del espacio se relaja al permitir la curvatura del espacio. En este espacio curvo se define una estructura ideal y sin frustraciones. Luego, se aplican distorsiones específicas a esta plantilla ideal para incrustarla en un espacio euclidiano tridimensional. La estructura final es una mezcla de regiones ordenadas, donde el orden local es similar al de la plantilla, y defectos que surgen de la incrustación. Entre los posibles defectos, las declinaciones juegan un papel importante.

Los ejemplos bidimensionales son útiles para comprender mejor el origen de la competencia entre las reglas locales y la geometría en general. Consideremos primero una disposición de discos idénticos (un modelo para un hipotético metal bidimensional) en un plano; Suponemos que la interacción entre discos es isotrópica y localmente tiende a disponer los discos de la forma más densa posible. La mejor disposición para tres discos es trivialmente un triángulo equilátero con los centros de los discos ubicados en los vértices del triángulo. Por tanto, el estudio de la estructura de largo alcance puede reducirse al de teselas planas con triángulos equiláteros. Una solución bien conocida es la del mosaico triangular con total compatibilidad entre las reglas locales y globales: el sistema se dice "no frustrado".
Pero ahora, se supone que la energía de interacción es mínima cuando los átomos se ubican en los vértices de un pentágono regular . Intentar propagar a larga distancia un empaquetamiento de estos pentágonos que comparten aristas (enlaces atómicos) y vértices (átomos) es imposible. Esto se debe a la imposibilidad de revestir un plano con pentágonos regulares, simplemente porque el ángulo del vértice del pentágono no divide a 2 π . Tres de estos pentágonos pueden caber fácilmente en un vértice común, pero queda un espacio entre dos aristas. Es este tipo de discrepancia lo que se llama "frustración geométrica". Hay una manera de superar esta dificultad. Dejemos que la superficie a revestir esté libre de cualquier topología presupuesta y construyamos el mosaico con una aplicación estricta de la regla de interacción local. En este sencillo ejemplo, observamos que la superficie hereda la topología de una esfera y por tanto recibe una curvatura. La estructura final, aquí un dodecaedro pentagonal, permite una perfecta propagación del orden pentagonal. Se denomina modelo "ideal" (libre de defectos) para la estructura considerada.

La estabilidad de los metales es una cuestión de larga data de la física del estado sólido, que sólo puede entenderse en el marco de la mecánica cuántica teniendo en cuenta adecuadamente la interacción entre los iones cargados positivamente y los electrones de valencia y conducción. Sin embargo, es posible utilizar una imagen muy simplificada del enlace metálico y mantener solo interacciones de tipo isotrópico, lo que lleva a estructuras que pueden representarse como esferas densamente empaquetadas. Y, de hecho, las estructuras metálicas cristalinas simples son a menudo redes cúbicas centradas en las caras (fcc) o hexagonales (hcp). Hasta cierto punto, los metales amorfos y los cuasicristales también pueden modelarse mediante empaquetamiento estrecho de esferas. El orden atómico local está bien modelado por un empaquetamiento estrecho de tetraedros, lo que conduce a un orden icosaédrico imperfecto.
Un tetraedro regular es la configuración más densa para el empaquetamiento de cuatro esferas iguales. Por lo tanto, el problema del empaquetamiento aleatorio denso de esferas duras se puede mapear en el problema del empaquetamiento tetraédrico . Es un ejercicio práctico intentar empacar pelotas de tenis de mesa para formar únicamente configuraciones tetraédricas. Se comienza con cuatro bolas dispuestas como un tetraedro perfecto, y se intenta ir añadiendo nuevas esferas, mientras se forman nuevos tetraedros. La siguiente solución, con cinco bolas, es trivialmente dos tetraedros que comparten una cara común; tenga en cuenta que ya con esta solución, la estructura fcc, que contiene agujeros tetraédricos individuales, no muestra tal configuración (los tetraedros comparten aristas, no caras). Con seis bolas se construyen tres tetraedros regulares y el cúmulo es incompatible con todas las estructuras cristalinas compactas (fcc y hcp). Agregar una séptima esfera da un nuevo grupo que consiste en dos bolas "axiales" que se tocan entre sí y otras cinco que tocan las dos últimas bolas, siendo la forma exterior una bipirámide pentagonal casi regular. Sin embargo, ahora nos enfrentamos a un verdadero problema de empaquetamiento, análogo al encontrado anteriormente con el mosaico pentagonal en dos dimensiones. El ángulo diédrico de un tetraedro no es conmensurable con 2 π ; en consecuencia, queda un agujero entre dos caras de tetraedros vecinos. Como consecuencia, un mosaico perfecto del espacio euclidiano R 3 es imposible con tetraedros regulares. La frustración tiene un carácter topológico: es imposible llenar el espacio euclidiano con tetraedros, incluso severamente distorsionados, si imponemos que un número constante de tetraedros (aquí cinco) compartan un borde común.
El siguiente paso es crucial: la búsqueda de una estructura libre de frustraciones que permita la curvatura en el espacio , para que las configuraciones locales se propaguen de manera idéntica y sin defectos por todo el espacio.

Veinte tetraedros irregulares se agrupan con un vértice común de tal manera que los doce vértices exteriores forman un icosaedro regular. De hecho, la longitud del borde del icosaedro l es ligeramente más larga que el radio de la circunsfera r ( l ≈ 1,05 r ). Hay solución con tetraedros regulares si el espacio no es euclidiano, sino esférico. Es el politopo {3,3,5}, usando la notación de Schläfli , también conocida como la de 600 celdas .
Hay ciento veinte vértices que pertenecen todos a la hiperesfera S 3 con radio igual a la proporción áurea ( φ = 1 + √ 5/2) si las aristas tienen una longitud unitaria. Las seiscientas celdas son tetraedros regulares agrupados por cinco alrededor de un borde común y por veinte alrededor de un vértice común. Esta estructura se llama politopo (ver Coxeter ), que es el nombre general en dimensión superior en la serie que contiene polígonos y poliedros. Incluso si esta estructura está incrustada en cuatro dimensiones, se ha considerado como una variedad tridimensional (curva). Este punto es conceptualmente importante por la siguiente razón. Los modelos ideales que se han introducido en el espacio curvo son las plantillas curvas tridimensionales. Localmente parecen modelos euclidianos tridimensionales. Entonces, el politopo {3,3,5}, que es un mosaico de tetraedros, proporciona una estructura atómica muy densa si los átomos están ubicados en sus vértices. Por lo tanto, se utiliza naturalmente como modelo para los metales amorfos, pero no hay que olvidar que esto se consigue al precio de sucesivas idealizaciones.