
En matemáticas , la teoría de Galois , introducida originalmente por Évariste Galois , establece una conexión entre la teoría de campos y la teoría de grupos . Esta conexión, el teorema fundamental de la teoría de Galois , permite reducir ciertos problemas de la teoría de campos a la teoría de grupos, lo que los hace más simples y fáciles de entender.
Galois introdujo el tema de estudio de las raíces de los polinomios . Esto le permitió caracterizar las ecuaciones polinómicas que se pueden resolver mediante radicales en términos de propiedades del grupo de permutación de sus raíces: una ecuación se puede resolver mediante radicales si sus raíces se pueden expresar mediante una fórmula que involucra solo números enteros , raíces n -ésimas y las cuatro operaciones aritméticas básicas . Esto generaliza ampliamente el teorema de Abel-Ruffini , que afirma que un polinomio general de grado al menos cinco no se puede resolver mediante radicales.
La teoría de Galois se ha utilizado para resolver problemas clásicos, incluyendo demostrar que dos problemas de la antigüedad no pueden resolverse tal como fueron planteados ( duplicar el cubo y trisecar el ángulo ) y caracterizar los polígonos regulares que son construibles (esta caracterización fue dada previamente por Gauss pero sin la prueba de que la lista de polígonos construibles estaba completa; todas las pruebas conocidas de que esta caracterización es completa requieren la teoría de Galois).
El trabajo de Galois fue publicado por Joseph Liouville catorce años después de su muerte. La teoría tardó más en popularizarse entre los matemáticos y en ser bien comprendida.
La teoría de Galois se ha generalizado a las conexiones de Galois y a la teoría de Galois de Grothendieck .
El nacimiento y desarrollo de la teoría de Galois estuvo motivado por la siguiente pregunta, que fue una de las principales cuestiones matemáticas abiertas hasta principios del siglo XIX:
¿Existe una fórmula para las raíces de una ecuación polinomial de quinto grado (o superior) en términos de los coeficientes del polinomio, utilizando solo las operaciones algebraicas habituales (suma, resta, multiplicación, división) y la aplicación de radicales (raíces cuadradas, raíces cúbicas, etc.)?
El teorema de Abel-Ruffini proporciona un contraejemplo que demuestra que existen ecuaciones polinómicas para las que no puede existir una fórmula de este tipo. La teoría de Galois proporciona una respuesta mucho más completa a esta pregunta, al explicar por qué es posible resolver algunas ecuaciones, incluidas todas las de grado cuatro o inferior, de la manera antes descrita, y por qué no es posible para la mayoría de las ecuaciones de grado cinco o superior. Además, proporciona un medio para determinar si una ecuación particular puede resolverse que es conceptualmente claro y fácil de expresar como un algoritmo .
La teoría de Galois también proporciona una visión clara de las cuestiones relativas a los problemas de construcción con regla y compás . Proporciona una caracterización elegante de las relaciones de longitudes que se pueden construir con este método. Con esto, resulta relativamente fácil responder a problemas clásicos de geometría como
La teoría de Galois se originó en el estudio de funciones simétricas : los coeficientes de un polinomio mónico son ( hasta el signo) los polinomios simétricos elementales en las raíces. Por ejemplo, ( x – a )( x – b ) = x 2 – ( a + b ) x + ab , donde 1, a + b y ab son los polinomios elementales de grado 0, 1 y 2 en dos variables.
Esto fue formalizado por primera vez por el matemático francés del siglo XVI François Viète , en las fórmulas de Viète , para el caso de raíces reales positivas. En opinión del matemático británico del siglo XVIII Charles Hutton , [2] la expresión de los coeficientes de un polinomio en términos de las raíces (no solo para raíces positivas) fue comprendida por primera vez por el matemático francés del siglo XVII Albert Girard ; Hutton escribe:
...[Girard fue] la primera persona que comprendió la doctrina general de la formación de los coeficientes de las potencias a partir de la suma de las raíces y sus productos. Fue el primero que descubrió las reglas para sumar las potencias de las raíces de cualquier ecuación.
En este sentido, el discriminante es una función simétrica en las raíces que refleja propiedades de las raíces: es cero si y solo si el polinomio tiene una raíz múltiple, y para polinomios cuadráticos y cúbicos es positivo si y solo si todas las raíces son reales y distintas, y negativo si y solo si hay un par de raíces complejas conjugadas distintas. Ver Discriminante: Naturaleza de las raíces para más detalles.
La cúbica fue resuelta parcialmente por primera vez por el matemático italiano del siglo XV-XVI Scipione del Ferro , quien sin embargo no publicó sus resultados; este método, sin embargo, solo resolvía un tipo de ecuación cúbica. Esta solución fue redescubierta luego de forma independiente en 1535 por Niccolò Fontana Tartaglia , quien la compartió con Gerolamo Cardano , pidiéndole que no la publicara. Cardano luego extendió esto a muchos otros casos, usando argumentos similares; vea más detalles en El método de Cardano . Después del descubrimiento del trabajo de del Ferro, sintió que el método de Tartaglia ya no era un secreto, y por lo tanto publicó su solución en su Ars Magna de 1545. [3] Su estudiante Lodovico Ferrari resolvió el polinomio de cuarto grado; su solución también fue incluida en Ars Magna. Sin embargo, en este libro Cardano no proporcionó una "fórmula general" para la solución de una ecuación cúbica, ya que no tenía a su disposición ni números complejos ni la notación algebraica para poder describir una ecuación cúbica general. Con el beneficio de la notación moderna y los números complejos, las fórmulas de este libro sí funcionan en el caso general, pero Cardano no lo sabía. Fue Rafael Bombelli quien logró comprender cómo trabajar con números complejos para resolver todas las formas de ecuación cúbica.
Un paso más allá fue el artículo de 1770 Réflexions sur la résolution algébrique des équations del matemático franco-italiano Joseph Louis Lagrange , en su método de los resolventes de Lagrange , donde analizó la solución de Cardano y Ferrari de las ecuaciones cúbicas y cuárticas considerándolas en términos de permutaciones de las raíces, lo que produjo un polinomio auxiliar de grado inferior, proporcionando una comprensión unificada de las soluciones y sentando las bases para la teoría de grupos y la teoría de Galois. Sin embargo, de manera crucial, no consideró la composición de permutaciones. El método de Lagrange no se extendió a las ecuaciones de quinto grado o superiores, porque el resolvente tenía un grado superior.
En 1799, Paolo Ruffini casi demostró que la ecuación de quinto grado no tenía soluciones generales por radicales , ya que su idea clave fue utilizar grupos de permutaciones , no solo una única permutación. Su solución contenía una brecha que Cauchy consideró menor, aunque no se solucionó hasta el trabajo del matemático noruego Niels Henrik Abel , quien publicó una prueba en 1824, estableciendo así el teorema de Abel-Ruffini .
Aunque Ruffini y Abel establecieron que la ecuación de quinto grado general no podía resolverse, algunas ecuaciones de quinto grado particulares sí pueden resolverse, como x 5 - 1 = 0 , y el criterio preciso por el cual una ecuación de quinto grado dada o un polinomio superior podía determinarse como resoluble o no fue dado por Évariste Galois , quien demostró que si un polinomio era resoluble o no era equivalente a si el grupo de permutación de sus raíces -en términos modernos, su grupo de Galois- tenía o no una cierta estructura -en términos modernos, si era o no un grupo resoluble- . Este grupo siempre era resoluble para polinomios de grado cuatro o menos, pero no siempre así para polinomios de grado cinco y mayores, lo que explica por qué no hay una solución general en grados superiores.

En 1830, Galois (a la edad de 18 años) presentó a la Academia de Ciencias de París una memoria sobre su teoría de la solubilidad por radicales; el artículo de Galois fue finalmente rechazado en 1831 por ser demasiado esquemático y por dar una condición en términos de las raíces de la ecuación en lugar de sus coeficientes. Galois murió en un duelo en 1832, y su artículo, " Mémoire sur les conditions de résolubilité des équations par radicaux ", permaneció inédito hasta 1846, cuando fue publicado por Joseph Liouville acompañado de algunas de sus propias explicaciones. [4] Antes de esta publicación, Liouville anunció el resultado de Galois a la Academia en un discurso que pronunció el 4 de julio de 1843. [5] Según Allan Clark, la caracterización de Galois "reemplaza dramáticamente el trabajo de Abel y Ruffini". [6]
La teoría de Galois era notoriamente difícil de entender para sus contemporáneos, especialmente al nivel en que podían expandirla. Por ejemplo, en su comentario de 1846, Liouville pasó por alto por completo el núcleo teórico de grupos del método de Galois. [7] Joseph Alfred Serret , que asistió a algunas de las charlas de Liouville, incluyó la teoría de Galois en su libro de texto Cours d' algèbre supérieure de 1866 (tercera edición) . El alumno de Serret, Camille Jordan , tuvo una comprensión aún mejor reflejada en su libro de 1870 Traité des substitutions et des équations algébriques . Fuera de Francia, la teoría de Galois permaneció más oscura durante un período más largo. En Gran Bretaña, Cayley no logró comprender su profundidad y los libros de texto de álgebra británicos populares ni siquiera mencionaron la teoría de Galois hasta mucho después del cambio de siglo. En Alemania, los escritos de Kronecker se centraron más en el resultado de Abel. Dedekind escribió poco sobre la teoría de Galois, pero dio una conferencia sobre ella en Göttingen en 1858, mostrando una muy buena comprensión. [8] Los libros de Eugen Netto de la década de 1880, basados en el Traité de Jordan , hicieron que la teoría de Galois fuera accesible a una audiencia alemana y estadounidense más amplia, al igual que el libro de texto de álgebra de Heinrich Martin Weber de 1895. [9]
Dado un polinomio, puede ser que algunas de las raíces estén conectadas por varias ecuaciones algebraicas . Por ejemplo, puede ser que para dos de las raíces, digamos A y B , que A 2 + 5 B 3 = 7. La idea central de la teoría de Galois es considerar permutaciones (o reordenamientos) de las raíces de modo que cualquier ecuación algebraica satisfecha por las raíces siga satisfecha después de que las raíces hayan sido permutadas. Originalmente, la teoría había sido desarrollada para ecuaciones algebraicas cuyos coeficientes son números racionales . Se extiende naturalmente a ecuaciones con coeficientes en cualquier cuerpo , pero esto no se considerará en los ejemplos simples a continuación.
Estas permutaciones juntas forman un grupo de permutaciones , también llamado grupo de Galois del polinomio, que se describe explícitamente en los siguientes ejemplos.
Considere la ecuación cuadrática
Usando la fórmula cuadrática , encontramos que las dos raíces son
Ejemplos de ecuaciones algebraicas satisfechas por A y B incluyen
y
Si intercambiamos A y B en cualquiera de las dos últimas ecuaciones obtenemos otra afirmación verdadera. Por ejemplo, la ecuación A + B = 4 se convierte en B + A = 4. Es más generalmente cierto que esto se cumple para cada posible relación algebraica entre A y B tal que todos los coeficientes sean racionales ; es decir, en cualquier relación de este tipo, intercambiar A y B produce otra relación verdadera. Esto resulta de la teoría de polinomios simétricos , que, en este caso, puede reemplazarse por manipulaciones de fórmulas que involucran el teorema del binomio .
Se podría objetar que A y B están relacionados por la ecuación algebraica A − B − 2 √ 3 = 0 , que no sigue siendo cierta cuando A y B se intercambian. Sin embargo, esta relación no se considera aquí, porque tiene el coeficiente −2 √ 3 que no es racional .
Concluimos que el grupo de Galois del polinomio x 2 − 4 x + 1 consta de dos permutaciones: la permutación identidad que deja A y B intactos, y la permutación de transposición que intercambia A y B. Como todos los grupos con dos elementos son isomorfos , este grupo de Galois es isomorfo al grupo multiplicativo {1, −1} .
Una discusión similar se aplica a cualquier polinomio cuadrático ax 2 + bx + c , donde a , b y c son números racionales.
Considere el polinomio
Completando el cuadrado de una manera inusual, también se puede escribir como
Aplicando la fórmula cuadrática a cada factor, se ve que las cuatro raíces son
Entre las 24 permutaciones posibles de estas cuatro raíces, cuatro son particularmente simples, las que consisten en el cambio de signo de 0, 1 o 2 raíces cuadradas. Forman un grupo isomorfo al cuatrigrupo de Klein .
La teoría de Galois implica que, como el polinomio es irreducible, el grupo de Galois tiene al menos cuatro elementos. Para demostrar que el grupo de Galois está formado por estas cuatro permutaciones, basta con demostrar que cada elemento del grupo de Galois está determinado por la imagen de A , lo que se puede demostrar de la siguiente manera.
Los miembros del grupo de Galois deben preservar cualquier ecuación algebraica con coeficientes racionales que involucren a A , B , C y D.
Entre estas ecuaciones tenemos:
De ello se deduce que, si φ es una permutación que pertenece al grupo de Galois, debemos tener:
Esto implica que la permutación está bien definida por la imagen de A , y que el grupo de Galois tiene 4 elementos, que son:
Esto implica que el grupo de Galois es isomorfo al cuatro-grupo de Klein .
En el enfoque moderno, se comienza con una extensión de campo L / K (léase " L sobre K ") y se examina el grupo de automorfismos de L que fijan K. Consulte el artículo sobre grupos de Galois para obtener más explicaciones y ejemplos.
La conexión entre los dos enfoques es la siguiente. Los coeficientes del polinomio en cuestión deben elegirse a partir del campo base K . El campo superior L debe ser el campo obtenido al adjuntar las raíces del polinomio en cuestión al campo base K . Cualquier permutación de las raíces que respete las ecuaciones algebraicas como se describió anteriormente da lugar a un automorfismo de L / K , y viceversa.
En el primer ejemplo anterior, estábamos estudiando la extensión Q ( √ 3 )/ Q , donde Q es el campo de los números racionales , y Q ( √ 3 ) es el campo obtenido a partir de Q al adjuntar √ 3 . En el segundo ejemplo, estábamos estudiando la extensión Q ( A , B , C , D )/ Q .
El enfoque moderno tiene varias ventajas sobre el enfoque del grupo de permutación.
La noción de grupo resoluble en teoría de grupos permite determinar si un polinomio es resoluble en radicales, dependiendo de si su grupo de Galois tiene la propiedad de solubilidad. En esencia, cada extensión de campo L / K corresponde a un grupo factorial en una serie de composición del grupo de Galois. Si un grupo factorial en la serie de composición es cíclico de orden n , y si en la extensión de campo correspondiente L / K el campo K ya contiene una raíz n primitiva de la unidad , entonces es una extensión radical y los elementos de L pueden entonces expresarse utilizando la raíz n ésima de algún elemento de K .
Si todos los grupos de factores en su serie de composición son cíclicos, el grupo de Galois se llama resoluble y todos los elementos del campo correspondiente se pueden encontrar tomando repetidamente raíces, productos y sumas de elementos del campo base (generalmente Q ).
Uno de los grandes triunfos de la teoría de Galois fue la prueba de que para cada n > 4 , existen polinomios de grado n que no son resolubles por radicales (esto fue demostrado independientemente, utilizando un método similar, por Niels Henrik Abel unos años antes, y es el teorema de Abel-Ruffini ), y una forma sistemática de probar si un polinomio específico es resoluble por radicales. El teorema de Abel-Ruffini resulta del hecho de que para n > 4 el grupo simétrico S n contiene un subgrupo simple , no cíclico y normal , a saber, el grupo alternado A n .
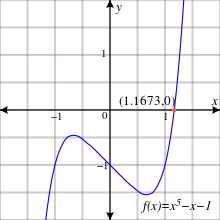
Van der Waerden [10] cita el polinomio f ( x ) = x 5 − x − 1 .
Según el teorema de la raíz racional , este no tiene ceros racionales.
Tampoco tiene factores lineales módulo 2 o 3.
El grupo de Galois de f ( x ) módulo 2 es cíclico de orden 6, porque f ( x ) módulo 2 se factoriza en polinomios de órdenes 2 y 3, ( x 2 + x + 1)( x 3 + x 2 + 1) .
f ( x ) módulo 3 no tiene factor lineal ni cuadrático y, por lo tanto, es irreducible. Por lo tanto, su grupo de Galois módulo 3 contiene un elemento de orden 5.
Se sabe [11] que un grupo de Galois módulo primo es isomorfo a un subgrupo del grupo de Galois sobre los racionales. Un grupo de permutación sobre 5 objetos con elementos de órdenes 6 y 5 debe ser el grupo simétrico S 5 , que es por tanto el grupo de Galois de f ( x ) .
Este es uno de los ejemplos más simples de un polinomio de quinto grado no resoluble. Según Serge Lang , a Emil Artin le gustaba este ejemplo. [12]
El problema de Galois inverso es encontrar una extensión de campo con un grupo de Galois dado.
Mientras no se especifique también el campo fundamental , el problema no es muy difícil, y todos los grupos finitos ocurren como grupos de Galois. Para mostrar esto, se puede proceder de la siguiente manera. Elija un campo K y un grupo finito G . El teorema de Cayley dice que G es (salvo isomorfismo) un subgrupo del grupo simétrico S sobre los elementos de G . Elija indeterminados { x α } , uno para cada elemento α de G , y adjúntelos a K para obtener el campo F = K ({ x α }) . Dentro de F está contenido el campo L de funciones racionales simétricas en { x α } . El grupo de Galois de F / L es S , por un resultado básico de Emil Artin. G actúa sobre F por restricción de la acción de S . Si el campo fijo de esta acción es M , entonces, por el teorema fundamental de la teoría de Galois , el grupo de Galois de F / M es G .
Por otra parte, es un problema abierto si cada grupo finito es el grupo de Galois de una extensión de campo del campo Q de los números racionales. Igor Shafarevich demostró que cada grupo finito resoluble es el grupo de Galois de alguna extensión de Q . Varias personas han resuelto el problema inverso de Galois para grupos simples no abelianos seleccionados . Se ha demostrado la existencia de soluciones para todos menos posiblemente uno ( grupo de Mathieu M 23 ) de los 26 grupos simples esporádicos. Incluso hay un polinomio con coeficientes enteros cuyo grupo de Galois es el grupo Monster .
En la forma mencionada anteriormente, incluyendo en particular el teorema fundamental de la teoría de Galois , la teoría solo considera extensiones de Galois, que son en particular separables. Las extensiones de campo generales se pueden dividir en una extensión de campo separable, seguida de una extensión de campo puramente inseparable . Para una extensión puramente inseparable F / K , existe una teoría de Galois donde el grupo de Galois se reemplaza por el espacio vectorial de derivaciones , , es decir, K - endomorfismos lineales de F que satisfacen la regla de Leibniz. En esta correspondencia, se asigna un campo intermedio E. Por el contrario, un subespacio que satisface condiciones adicionales apropiadas se mapea a . Bajo el supuesto , Jacobson (1944) demostró que esto establece una correspondencia uno a uno. La condición impuesta por Jacobson ha sido eliminada por Brantner & Waldron (2020), al dar una correspondencia utilizando nociones de geometría algebraica derivada .