Anillo conmutativo

estructura algebraica

En matemáticas , un anillo conmutativo es un anillo en el que la operación de multiplicación es conmutativa . El estudio de los anillos conmutativos se llama álgebra conmutativa . Complementariamente, el álgebra no conmutativa es el estudio de las propiedades de los anillos que no son específicas de los anillos conmutativos. Esta distinción resulta del gran número de propiedades fundamentales de los anillos conmutativos que no se extienden a los anillos no conmutativos.

Definición y primeros ejemplos.

Definición

Un anillo es un conjunto dotado de dos operaciones binarias , es decir, operaciones que combinan dos elementos cualesquiera del anillo con un tercero. Se llaman suma y multiplicación y comúnmente se denotan por " " y " "; por ejemplo y . Para formar un anillo, estas dos operaciones deben satisfacer una serie de propiedades: el anillo tiene que ser un grupo abeliano en la suma y un monoide en la multiplicación, donde la multiplicación se distribuye sobre la suma; es decir, . Los elementos de identidad para la suma y la multiplicación se denotan y , respectivamente. ${\displaystyle R}$ ${\displaystyle +}$ ${\displaystyle \cdot }$ ${\displaystyle a+b}$ ${\displaystyle a\cdot b}$ ${\displaystyle a\cdot \left(b+c\right)=\left(a\cdot b\right)+\left(a\cdot c\right)}$ ${\displaystyle 0}$ ${\displaystyle 1}$

Si la multiplicación es conmutativa, es decir

$${\displaystyle a\cdot b=b\cdot a,}$$

conmutativo ${\displaystyle R}$

Primeros ejemplos

Un ejemplo importante, y en cierto sentido crucial, es el anillo de números enteros con las dos operaciones de suma y multiplicación. Como la multiplicación de números enteros es una operación conmutativa, este es un anillo conmutativo. Generalmente se denota como una abreviatura de la palabra alemana Zahlen (números). ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Z} }$

Un campo es un anillo conmutativo donde cada elemento distinto de cero es invertible; es decir, tiene un inverso multiplicativo tal que . Por tanto, por definición, cualquier campo es un anillo conmutativo. Los números racionales , reales y complejos forman campos. ${\displaystyle 0\not =1}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a\cdot b=1}$

Si es un anillo conmutativo dado, entonces el conjunto de todos los polinomios de la variable cuyos coeficientes están en forma el anillo polinomial , denotado . Lo mismo ocurre con varias variables. ${\displaystyle R}$ ${\displaystyle X}$ ${\displaystyle R}$ ${\displaystyle R\left[X\right]}$

Si es algún espacio topológico , por ejemplo un subconjunto de algunas funciones continuas de valores reales o complejos , forman un anillo conmutativo. Lo mismo ocurre con las funciones diferenciables u holomorfas , cuando se definen los dos conceptos, como por ejemplo para una variedad compleja . ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle V}$ ${\displaystyle V}$

Divisibilidad

A diferencia de los campos, donde cada elemento distinto de cero es multiplicativamente invertible, el concepto de divisibilidad de los anillos es más rico. Un elemento de anillo se llama unidad si posee un inverso multiplicativo. Otro tipo particular de elemento son los divisores de cero , es decir, un elemento tal que existe un elemento distinto de cero del anillo tal que . Si no posee divisores cero distintos de cero, se llama dominio integral (o dominio). Un elemento que satisface algún número entero positivo se llama nilpotente . ${\displaystyle a}$ ${\displaystyle R}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle ab=0}$ ${\displaystyle R}$ ${\displaystyle a}$ ${\displaystyle a^{n}=0}$ ${\displaystyle n}$

Localizaciones

La localización de un anillo es un proceso en el que algunos elementos se vuelven invertibles, es decir, se añaden al anillo inversos multiplicativos. Concretamente, si es un subconjunto multiplicativamente cerrado de (es decir, siempre que así sea ), entonces la localización de at , o anillo de fracciones con denominadores en , generalmente denotado consta de símbolos ${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle s,t\in S}$ ${\displaystyle st}$ ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S^{-1}R}$

${\displaystyle {\frac {r}{s}}}$con ${\displaystyle r\in R,s\in S}$

sujeto a ciertas reglas que imitan la cancelación familiar de los números racionales. De hecho, en este idioma es la localización de números enteros distintos de cero. Esta construcción funciona para cualquier dominio integral en lugar de . La localización es un campo, llamado campo cociente de . ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle R}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \left(R\setminus \left\{0\right\}\right)^{-1}R}$ ${\displaystyle R}$

Ideales y módulos

Muchas de las siguientes nociones también existen para anillos no necesariamente conmutativos, pero las definiciones y propiedades suelen ser más complicadas. Por ejemplo, todos los ideales en un anillo conmutativo son automáticamente bilaterales , lo que simplifica considerablemente la situación.

Módulos

Para un anillo , un módulo es como lo que es un espacio vectorial para un campo. Es decir, se pueden agregar elementos en un módulo; se pueden multiplicar por elementos de sujeto a los mismos axiomas que para un espacio vectorial. ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle M}$ ${\displaystyle R}$

El estudio de módulos es significativamente más complicado que el de espacios vectoriales , ya que hay módulos que no tienen base alguna , es decir, que no contienen un conjunto generador cuyos elementos sean linealmente independientes . Un módulo que tiene una base se llama módulo libre y un submódulo de un módulo libre no necesita ser libre.

Un módulo de tipo finito es un módulo que tiene un conjunto de expansión finito. Los módulos de tipo finito juegan un papel fundamental en la teoría de anillos conmutativos, similar al papel de los espacios vectoriales de dimensión finita en álgebra lineal . En particular, los anillos noetherianos (ver también § Anillos noetherianos , más abajo) se pueden definir como anillos tales que cada submódulo de un módulo de tipo finito también es de tipo finito.

Ideales

Los ideales de un anillo son los submódulos de , es decir, los módulos contenidos en . Más detalladamente, un ideal es un subconjunto no vacío de tal que para todo en y en , ambos y están en . Para diversas aplicaciones, comprender los ideales de un anillo es de particular importancia, pero a menudo se procede estudiando los módulos en general. ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle I}$ ${\displaystyle R}$ ${\displaystyle r}$ ${\displaystyle R}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle I}$ ${\displaystyle ri}$ ${\displaystyle i+j}$ ${\displaystyle I}$

Cualquier anillo tiene dos ideales, a saber, el ideal cero y el anillo completo. Estos dos ideales son los únicos que precisamente son un campo. Dado cualquier subconjunto de (donde hay algún conjunto de índices), el ideal generado por es el ideal más pequeño que contiene . De manera equivalente, está dado por combinaciones lineales finitas. ${\displaystyle \left\{0\right\}}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle F=\left\{f_{j}\right\}_{j\in J}}$ ${\displaystyle R}$ ${\displaystyle J}$ ${\displaystyle F}$ ${\displaystyle F}$

$${\displaystyle r_{1}f_{1}+r_{2}f_{2}+\dots +r_{n}f_{n}.}$$

Principales dominios ideales

Si consta de un solo elemento , el ideal generado por consta de los múltiplos de , es decir, los elementos de la forma para elementos arbitrarios . A tal ideal se le llama ideal principal . Si todo ideal es un ideal principal, se llama anillo ideal principal ; dos casos importantes son y , el anillo polinómico sobre un campo . Estos dos son dominios sumarios, por lo que se denominan dominios ideales principales . ${\displaystyle F}$ ${\displaystyle r}$ ${\displaystyle F}$ ${\displaystyle r}$ ${\displaystyle rs}$ ${\displaystyle s}$ ${\displaystyle R}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle k\left[X\right]}$ ${\displaystyle k}$

A diferencia de los anillos generales, para un dominio ideal principal, las propiedades de los elementos individuales están fuertemente ligadas a las propiedades del anillo en su conjunto. Por ejemplo, cualquier dominio ideal principal es un dominio de factorización único (UFD), lo que significa que cualquier elemento es un producto de elementos irreducibles, de una manera única (hasta el reordenamiento de los factores). Aquí, un elemento en un dominio se llama irreducible si la única forma de expresarlo como un producto ${\displaystyle R}$ ${\displaystyle a}$

$${\displaystyle a=bc,}$$

la teoría de camposlos polinomios irreduciblesteorema fundamental de la aritmética ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle k\left[X\right]}$ ${\displaystyle k}$ ${\displaystyle \mathbb {Z} }$

Un elemento es elemento primo si siempre que se divide un producto , se divide o . En un dominio, ser primo implica ser irreducible. Lo contrario es cierto en un dominio de factorización único, pero falso en general. ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle bc}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

Anillo de factores

La definición de ideales es tal que "dividir" "hacia afuera" da otro anillo, el anillo factorial : es el conjunto de clases laterales de junto con las operaciones ${\displaystyle I}$ ${\displaystyle R/I}$ ${\displaystyle I}$

$${\displaystyle \left(a+I\right)+\left(b+I\right)=\left(a+b\right)+I}$$

la aritmética modular ${\displaystyle \left(a+I\right)\left(b+I\right)=ab+I}$ ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ ${\displaystyle \mathbb {Z} _{n}}$ ${\displaystyle n}$ ${\displaystyle n}$

Un ideal es adecuado si es estrictamente más pequeño que todo el anillo. Un ideal que no está estrictamente contenido en ningún ideal propio se llama maximal . Un ideal es máximo si y sólo si es un campo. Excepto el anillo cero , cualquier anillo (con identidad) posee al menos un ideal máximo; esto se sigue del lema de Zorn . ${\displaystyle m}$ ${\displaystyle R/m}$

anillos noetherianos

Un anillo se llama Noetherian (en honor a Emmy Noether , quien desarrolló este concepto) si cada cadena ascendente de ideales

$${\displaystyle 0\subseteq I_{0}\subseteq I_{1}\subseteq \dots \subseteq I_{n}\subseteq I_{n+1}\dots }$$

los submódulos ${\displaystyle n}$

Ser noetheriano es una condición de finitud muy importante, y la condición se conserva en muchas operaciones que ocurren con frecuencia en geometría. Por ejemplo, si es noetheriano, también lo es el anillo polinómico (según el teorema de la base de Hilbert ), cualquier localización y también cualquier anillo factorial . ${\displaystyle R}$ ${\displaystyle R\left[X_{1},X_{2},\dots ,X_{n}\right]}$ ${\displaystyle S^{-1}R}$ ${\displaystyle R/I}$

Cualquier anillo no noetheriano es la unión de sus subanillos noetherianos. Este hecho, conocido como aproximación noetheriana, permite la extensión de ciertos teoremas a anillos no noetherianos. ${\displaystyle R}$

anillos artinianos

Un anillo se llama artiniano (en honor a Emil Artin ), si cada cadena descendente de ideales

$${\displaystyle R\supseteq I_{0}\supseteq I_{1}\supseteq \dots \supseteq I_{n}\supseteq I_{n+1}\dots }$$

${\displaystyle \mathbb {Z} }$

$${\displaystyle \mathbb {Z} \supsetneq 2\mathbb {Z} \supsetneq 4\mathbb {Z} \supsetneq 8\mathbb {Z} \dots }$$

teorema de Hopkins-Levitzki

Espectro de un anillo conmutativo

Ideales primordiales

Como se mencionó anteriormente, es un dominio de factorización único . Esto no es cierto para anillos más generales, como se dieron cuenta los algebristas en el siglo XIX. Por ejemplo, en ${\displaystyle \mathbb {Z} }$

$${\displaystyle \mathbb {Z} \left[{\sqrt {-5}}\right]}$$

$${\displaystyle 6=2\cdot 3=\left(1+{\sqrt {-5}}\right)\left(1-{\sqrt {-5}}\right).}$$

anillo de Dedekindanillo de números enteros en un campo numérico ${\displaystyle R}$ ${\displaystyle p}$ ${\displaystyle ab}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle p,}$ ${\displaystyle p.}$ ${\displaystyle \mathbb {Z} \left[{\sqrt {-5}}\right],}$ ${\displaystyle \mathbb {Z} \left[{\sqrt {-5}}\right]}$

Cualquier ideal maximal es un ideal primo o, más brevemente, es primo. Además, un ideal es primo si y sólo si el anillo de factores es un dominio integral. Demostrar que un ideal es primo o, equivalentemente, que un anillo no tiene divisores cero puede resultar muy difícil. Otra forma más de expresar lo mismo es decir que el complemento es multiplicativamente cerrado. La localización es lo suficientemente importante como para tener su propia notación: . Este anillo tiene sólo un ideal máximo, a saber . Estos anillos se denominan locales . ${\displaystyle I}$ ${\displaystyle R/I}$ ${\displaystyle R\setminus p}$ ${\displaystyle \left(R\setminus p\right)^{-1}R}$ ${\displaystyle R_{p}}$ ${\displaystyle pR_{p}}$

Espectro

Spec ( Z ) contiene un punto para el ideal cero. El cierre de este punto es todo el espacio. Los puntos restantes son los correspondientes a ideales ( p ), donde p es un número primo. Estos puntos están cerrados.

El espectro de un anillo , ^[a] denotado por , es el conjunto de todos los ideales primos de . Está equipado con una topología, la topología de Zariski , que refleja las propiedades algebraicas de : una base de subconjuntos abiertos está dada por ${\displaystyle R}$ ${\displaystyle {\text{Spec}}\ R}$ ${\displaystyle R}$ ${\displaystyle R}$

$${\displaystyle D\left(f\right)=\left\{p\in {\text{Spec}}\ R,f\not \in p\right\},}$$

fpfRpfR → R _fR → R / fR corresponden, después de dotar a los espectros de los anillos en cuestión de su topología de Zariski, a inmersiones abiertasR = Z ${\displaystyle f}$ ${\displaystyle f}$

El espectro contiene el conjunto de ideales máximos, que ocasionalmente se denomina mSpec ( R ). Para un campo algebraicamente cerrado k , mSpec (k[ T ₁ , ..., T _n ] / ( f ₁ , ..., f _m )) está en biyección con el conjunto

{ x =( x ₁ , ..., x _norte ) ∊ k ^norte

Por tanto, los ideales máximos reflejan las propiedades geométricas de los conjuntos solución de polinomios, lo que constituye una motivación inicial para el estudio de los anillos conmutativos. Sin embargo, la consideración de ideales no máximos como parte de las propiedades geométricas de un anillo es útil por varias razones. Por ejemplo, los ideales primos mínimos (es decir , los que no contienen estrictamente otros más pequeños) corresponden a los componentes irreducibles de Spec R. Para un anillo noetheriano R , Spec R tiene solo un número finito de componentes irreducibles. Se trata de una reformulación geométrica de la descomposición primaria , según la cual cualquier ideal puede descomponerse como producto de un número finito de ideales primarios . Este hecho es la generalización última de la descomposición en ideales primos en los anillos de Dedekind.

Esquemas afines

La noción de espectro es la base común del álgebra conmutativa y la geometría algebraica . La geometría algebraica procede dotando a Spec R de una gavilla (una entidad que recopila funciones definidas localmente, es decir, en distintos subconjuntos abiertos). La referencia del espacio y la gavilla se llama esquema afín . Dado un esquema afín, el anillo subyacente R se puede recuperar como las secciones globales de . Además, esta correspondencia uno a uno entre anillos y esquemas afines también es compatible con homomorfismos de anillos: cualquier f  : R → S da lugar a un mapa continuo en la dirección opuesta ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$

Spec S → Spec R , q ↦ f ⁻¹ ( q ), es decir , cualquier ideal primo de S se asigna a su preimagen bajo f , que es un ideal primo de R.

La equivalencia resultante de ambas categorías refleja acertadamente las propiedades algebraicas de los anillos de manera geométrica.

De manera similar al hecho de que las variedades están dadas localmente por subconjuntos abiertos de R ⁿ , los esquemas afines son modelos locales para esquemas , que son objeto de estudio en geometría algebraica. Por tanto, varias nociones relativas a los anillos conmutativos surgen de la intuición geométrica.

Dimensión

La dimensión Krull (o dimensión) dim R de un anillo R mide el "tamaño" de un anillo, en términos generales, contando elementos independientes en R . La dimensión de las álgebras sobre un campo k puede axiomatizarse mediante cuatro propiedades:

• La dimensión es una propiedad local: dim R = sup _{p ∊ Spec R} dim R _p .
• La dimensión es independiente de los elementos nilpotentes: si I ⊆ R es nilpotente entonces dim R = dim R / I .
• La dimensión permanece constante bajo una extensión finita: si S es una R -álgebra que se genera finitamente como un R -módulo, entonces dim S = dim R .
• La dimensión se calibra mediante dim k [ X ₁ , ..., X _n ] = n . Este axioma está motivado por considerar el anillo polinomial en n variables como un análogo algebraico del espacio n -dimensional .

La dimensión se define, para cualquier anillo R , como el supremo de longitudes n de cadenas de ideales primos.

pags ₀ ⊊ pags ₁ ⊊ ... ⊊ pags _norte .

Por ejemplo, un campo es de dimensión cero, ya que el único ideal primo es el ideal cero. Los números enteros son unidimensionales, ya que las cadenas tienen la forma (0) ⊊ ( p ), donde p es un número primo . Para los anillos no noetherianos, y también para los anillos no locales, la dimensión puede ser infinita, pero los anillos locales noetherianos tienen una dimensión finita. Entre los cuatro axiomas anteriores, los dos primeros son consecuencias elementales de la definición, mientras que los dos restantes dependen de hechos importantes en álgebra conmutativa , el teorema del ascenso y el teorema ideal principal de Krull .

Homomorfismos de anillo

Un homomorfismo de anillo o, más coloquialmente, simplemente un mapa , es un mapa f  : R → S tal que

f ( a + b ) = f ( a ) + f ( b ), f ( ab ) = f ( a ) f ( b ) y f (1) = 1.

Estas condiciones aseguran que f (0) = 0 . De manera similar a otras estructuras algebraicas, un homomorfismo de anillo es, por tanto, un mapa que es compatible con la estructura de los objetos algebraicos en cuestión. En tal situación, S también se llama R -álgebra, entendiendo que s en S puede multiplicarse por algún r de R , estableciendo

r · s  := f ( r ) · s .

El núcleo y la imagen de f están definidos por ker( f ) = { r ∈ R , f ( r ) = 0} y im( f ) = f ( R ) = { f ( r ), r ∈ R } . El núcleo es un ideal de R y la imagen es un subanillo de S.

Un homomorfismo de anillo se llama isomorfismo si es biyectivo. Un ejemplo de isomorfismo de anillo, conocido como teorema chino del resto , es

$${\displaystyle \mathbf {Z} /n=\bigoplus _{i=0}^{k}\mathbf {Z} /p_{i},}$$

n = p ₁ p ₂ ... p _knúmeros primos

Los anillos conmutativos, junto con los homomorfismos de anillo, forman una categoría . El anillo Z es el objeto inicial en esta categoría, lo que significa que para cualquier anillo conmutativo R , existe un homomorfismo de anillo único Z → R. Mediante este mapa, un número entero n puede considerarse como un elemento de R. Por ejemplo, la fórmula binomial

$${\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}}$$

abRR

La propiedad universal de S ⊗ _R T establece que para dos mapas cualesquiera S → W y T → W que hacen que el cuadrilátero exterior conmute, existe un mapa único S ⊗ _R T → W que hace que todo el diagrama conmute.

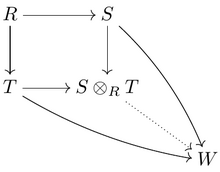
Dadas dos R -álgebras S y T , su producto tensorial

S ⊗ _R T

es nuevamente una R -álgebra conmutativa. En algunos casos, el producto tensorial puede servir para encontrar una T -álgebra que se relacione con Z como S se relaciona con R . Por ejemplo,

R [ X ] ⊗ _R T = T [ X ].

generación finita

Una R -álgebra S se llama finitamente generada (como un álgebra) si hay un número finito de elementos s ₁ , ..., s _n tales que cualquier elemento de s es expresable como un polinomio en s _i . De manera equivalente, S es isomorfo a

R [ T ₁ , ..., T _norte ] / I .

Una condición mucho más fuerte es que S se genera finitamente como un R -módulo , lo que significa que cualquier s puede expresarse como una R -combinación lineal de algún conjunto finito s ₁ , ..., s _n .

Anillos locales

Un anillo se llama local si tiene un solo ideal máximo, denotado por m . Para cualquier anillo R (no necesariamente local) , la localización

Rp _{_}

en un ideal primo p es local. Esta localización refleja las propiedades geométricas de Spec R "alrededor de p ". Varias nociones y problemas en álgebra conmutativa se pueden reducir al caso en que R es local, lo que hace que los anillos locales sean una clase de anillos particularmente estudiada. El campo residual de R se define como

k = R / m .

Cualquier R -módulo M produce un k -espacio vectorial dado por M / mM . El lema de Nakayama muestra que este pasaje preserva información importante: un módulo M generado finitamente es cero si y sólo si M / mM es cero.

Anillos locales regulares

La curva plana cúbica (roja) definida por la ecuación y ² = x ² ( x + 1 ) es singular en el origen, es decir, el anillo k [ x , y ] / y ² − x ² ( x + 1 ), es No es un anillo normal. El cono tangente (azul) es la unión de dos rectas, lo que también refleja la singularidad.

El espacio k -vectorial m / m ² es una encarnación algebraica del espacio cotangente . Informalmente, los elementos de m pueden considerarse como funciones que desaparecen en el punto p , mientras que m ² contiene los que desaparecen con un orden al menos 2. Para cualquier anillo local noetheriano R , la desigualdad

tenue _k m / m ² ≥ tenue R

es cierto, lo que refleja la idea de que el espacio cotangente ( o equivalentemente la tangente) tiene al menos la dimensión del espacio Spec R. Si la igualdad es cierta en esta estimación, R se llama anillo local regular . Un anillo local noetheriano es regular si y sólo si el anillo (que es el anillo de funciones en el cono tangente )

$${\displaystyle \bigoplus _{n}m^{n}/m^{n+1}}$$

k^[1][2]

Los anillos de valoración discretos están equipados con una función que asigna un número entero a cualquier elemento r . Este número, llamado valoración de r, puede considerarse informalmente como un orden cero o polar de r . Los anillos de valoración discretos son precisamente los anillos locales regulares unidimensionales. Por ejemplo, el anillo de gérmenes de funciones holomorfas en una superficie de Riemann es un anillo de valoración discreto.

Intersecciones completas

La cúbica retorcida (verde) es una intersección completa en la teoría de conjuntos, pero no una intersección completa.

Según el teorema ideal principal de Krull , un resultado fundamental en la teoría dimensional de los anillos , la dimensión de

R = k [ T ₁ , ..., T _r ] / ( f ₁ , ..., f _norte )

es al menos r - n . Un anillo R se denomina anillo de intersección completo si se puede presentar de manera que alcance este límite mínimo. Esta noción también se estudia principalmente para los anillos locales. Cualquier anillo local regular es un anillo de intersección completo, pero no a la inversa.

Un anillo R es una intersección completa en teoría de conjuntos si el anillo reducido asociado a R , es decir, el que se obtiene dividiendo todos los elementos nilpotentes, es una intersección completa. En 2017, en general se desconoce si las curvas en el espacio tridimensional son intersecciones completas en la teoría de conjuntos. ^[3]

Anillos de Cohen-Macaulay

La profundidad de un anillo local R es el número de elementos en alguna (o, como se puede mostrar, cualquier) secuencia regular máxima, es decir, una secuencia a ₁ , ..., a _n ∈ m tal que todos a _i no son -cero divisores en

R / ( a ₁ , ..., a _{i −1} ).

Para cualquier anillo noetheriano local, la desigualdad

profundidad( R ) ≤ tenue( R )

sostiene. Un anillo local en el que se produce la igualdad se denomina anillo de Cohen-Macaulay . Los anillos de intersección locales completos y, a fortiori, los anillos locales regulares son Cohen-Macaulay, pero no a la inversa. Cohen-Macaulay combina propiedades deseables de los anillos regulares (como la propiedad de ser anillos universalmente catenarios , lo que significa que la (co)dimensión de los números primos se comporta bien), pero también son más robustos al tomar cocientes que los anillos locales regulares. ^[4]

Construyendo anillos conmutativos

Hay varias formas de construir nuevos anillos a partir de los existentes. El objetivo de tales construcciones es a menudo mejorar determinadas propiedades del anillo para hacerlo más fácilmente comprensible. Por ejemplo, un dominio integral que está integralmente cerrado en su campo de fracciones se llama normal . Esta es una propiedad deseable, por ejemplo cualquier anillo unidimensional normal es necesariamente regular . Hacer ^{[ se necesita aclaración ]} un anillo normal se conoce como normalización .

Terminaciones

Si I es un ideal en un anillo conmutativo R , las potencias de I forman vecindades topológicas de 0 que permiten que R sea visto como un anillo topológico . Esta topología se llama topología I -ádica . Luego se puede completar R con respecto a esta topología. Formalmente, la terminación I -ádica es el límite inverso de los anillos R / I ⁿ . Por ejemplo, si k es un campo, k [[ X ]], el anillo de serie de potencias formal en una variable sobre k , es la terminación I -ádica de k [ X ] donde I es el ideal principal generado por X . Este anillo sirve como análogo algebraico del disco. De manera análoga, el anillo de enteros p -ádicos es la compleción de Z con respecto al ideal principal ( p ). Cualquier anillo que sea isomorfo a su propia terminación, se llama completo .

Los anillos locales completos satisfacen el lema de Hensel , que en términos generales permite extender soluciones (de varios problemas) sobre el campo de residuos k a R.

Nociones homológicas

Se han estudiado varios aspectos más profundos de los anillos conmutativos utilizando métodos del álgebra homológica . Hochster (2007) enumera algunas preguntas abiertas en esta área de investigación activa.

Módulos proyectivos y functores Ext.

Los módulos proyectivos se pueden definir como sumandos directos de módulos libres. Si R es local, cualquier módulo proyectivo generado finitamente es en realidad libre, lo que da contenido a una analogía entre módulos proyectivos y paquetes de vectores . ^[5] El teorema de Quillen-Suslin afirma que cualquier módulo proyectivo generado finitamente sobre k [ T ₁ , ..., T _n ] ( k un campo) es libre, pero en general estos dos conceptos difieren. Un anillo noetheriano local es regular si y sólo si su dimensión global es finita, digamos n , lo que significa que cualquier módulo R finitamente generado tiene una resolución por módulos proyectivos de longitud como máximo n .

La prueba de esta y otras afirmaciones relacionadas se basa en el uso de métodos homológicos, como el functor Ext . Este funtor es el funtor derivado del funtor.

Hom _R ( METRO , −).

El último functor es exacto si M es proyectivo, pero no en caso contrario: para un mapa sobreyectivo E → F de R -módulos, un mapa M → F no necesita extenderse a un mapa M → E. Los functores Ext superiores miden la falta de exactitud del functor Hom. La importancia de esta construcción estándar en las raíces del álgebra homológica se puede ver en el hecho de que un anillo noetheriano local R con campo de residuos k es regular si y sólo si

extensión ⁿ ( k , k )

desaparece para todos los suficientemente grandes n . Además, las dimensiones de estos grupos Ext, conocidos como números de Betti , crecen polinomialmente en n si y sólo si R es un anillo de intersección completo local . ^[6] Un argumento clave en tales consideraciones es el complejo de Koszul , que proporciona una resolución libre explícita del campo residual k de un anillo local R en términos de una secuencia regular.

Llanura

El producto tensorial es otro funtor no exacto relevante en el contexto de los anillos conmutativos: para un módulo R general M , el funtor

METRO ⊗ _R −

es exactamente exacto. Si es exacto, M se llama plano . Si R es local, cualquier módulo plano presentado finitamente está libre de rango finito y, por tanto, es proyectivo. A pesar de estar definida en términos de álgebra homológica, la planitud tiene profundas implicaciones geométricas. Por ejemplo, si un R -álgebra S es plano, las dimensiones de las fibras

S / pS = S ⊗ _R R / p

(para ideales primos p en R ) tienen la dimensión "esperada", es decir, tenue S − tenue R + tenue( R / p ) .

Propiedades

Según el teorema de Wedderburn , todo anillo de división finito es conmutativo y, por tanto, un campo finito . Otra condición que garantiza la conmutatividad de un anillo, debida a Jacobson , es la siguiente: para cada elemento r de R existe un número entero n > 1 tal que r ⁿ = r . ^[7] Si, r ² = r para cada r , el anillo se llama anillo booleano . También se conocen condiciones más generales que garantizan la conmutatividad de un anillo. ^[8]

Generalizaciones

Anillos conmutativos graduados

Un par de pantalones es un cobordismo entre un círculo y dos círculos disjuntos. Las clases de cobordismo, con el producto cartesiano como multiplicación y la unión disjunta como suma, forman el anillo de cobordismo .

Un anillo graduado R = ⨁ _{i ∊ Z} R _i se llama conmutativo graduado si, para todos los elementos homogéneos a y b ,

ab = (−1) ^{grados a ⋅ grados b} ba .

Si los R _i están conectados por diferenciales ∂ tales que se cumple una forma abstracta de la regla del producto , es decir,

∂( ab ) = ∂( a ) b + (−1) ^{grados a} a∂( b ),

R se llama álgebra graduada diferencial conmutativa (cdga). Un ejemplo es el complejo de formas diferenciales sobre una variedad , con la multiplicación dada por el producto exterior , es una cdga. La cohomología de un cdga es un anillo conmutativo graduado, a veces denominado anillo de cohomología . De esta manera surge una amplia gama de ejemplos de anillos graduados. Por ejemplo, el anillo de Lazard es el anillo de clases de cobordismo de variedades complejas.

Un anillo conmutativo graduado con respecto a una calificación de Z /2 (a diferencia de Z ) se llama superálgebra .

Una noción relacionada es un anillo casi conmutativo , lo que significa que R se filtra de tal manera que el anillo graduado asociado

gr R  := ⨁ F _yo R / ⨁ F _{yo −1} R

es conmutativo. Un ejemplo es el álgebra de Weyl y anillos más generales de operadores diferenciales .

Anillos conmutativos simpliciales

Un anillo conmutativo simplicial es un objeto simplicial en la categoría de anillos conmutativos. Son bloques de construcción para la geometría algebraica derivada (conectiva) . Una noción estrechamente relacionada pero más general es la de E _∞ -ring .

Aplicaciones de los anillos conmutativos

• Funciones holomorfas
• Teoría K algebraica
• Teoría K topológica
• Estructuras de poder divididas
• Vectores de wit
• Álgebra de Hecke (utilizada en la prueba de Wiles del último teorema de Fermat )
• Suena la época de Fontaine
• Álgebra de clusters
• Álgebra de convolución (de un grupo conmutativo)
• álgebra de frechet

Ver también

• Casi anillo , cierta generalización de un anillo conmutativo
• Divisibilidad (teoría de anillos) : elemento nilpotente , (ej. números duales )
• Ideales y módulos: Radical de un ideal , equivalencia de Morita
• Homomorfismos de anillo : elemento integral : teorema de Cayley-Hamilton , dominio integralmente cerrado , anillo de Krull , teorema de Krull-Akizuki , teorema de Mori-Nagata
• Primos: lema de evitación de primos , radical de Jacobson , radical nil de un anillo , espectro: espacio compacto , anillo conexo , cálculo diferencial sobre álgebras conmutativas , teorema de Banach-Stone
• Anillos locales : Anillo local de Gorenstein (también usado en la prueba de Wiles del último teorema de Fermat ): Dualidad (matemáticas) , Eben Matlis ; Módulo de dualización , teorema de Popescu , teorema de aproximación de Artin .

Notas

1. Esta noción puede estar relacionada con el espectro de un operador lineal; consulte Espectro de una representación de C*-álgebra y Gelfand .

Citas

1. Matsumura 1989, pág. 143, §7, Observaciones
2. Matsumura 1989, §19, Teorema 48
3. Lyubeznik 1989
4. Eisenbud 1995, Corolario 18.10, Proposición 18.13
5. Véase también el teorema de Serre-Swan
6. Christensen, Striuli y Veliche 2010
7. Jacobson 1945
8. Pinter-Lucke 2007

Referencias

• Christensen, Lars Winther; Struli, Janet; Veliche, Oana (2010), "Crecimiento en la resolución inyectiva mínima de un anillo local", Revista de la Sociedad Matemática de Londres , Segunda Serie, 81 (1): 24–44, arXiv : 0812.4672 , doi :10.1112/jlms/jdp058 , S2CID  14764965
• Eisenbud, David (1995), Álgebra conmutativa. Con miras a la geometría algebraica. , Textos de Graduado en Matemáticas , vol. 150, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-94268-1, señor  1322960
• Hochster, Melvin (2007), "Conjeturas homológicas, antiguas y nuevas", Illinois J. Math. , 51 (1): 151–169, doi : 10.1215/ijm/1258735330
• Jacobson, Nathan (1945), "Teoría de la estructura de álgebras algebraicas de grado acotado", Annals of Mathematics , 46 (4): 695–707, doi :10.2307/1969205, ISSN  0003-486X, JSTOR  1969205
• Lyubeznik, Gennady (1989), "Un estudio de problemas y resultados sobre el número de ecuaciones definitorias", Representaciones, resoluciones y números entrelazados , págs. 375–390, Zbl  0753.14001
• Matsumura, Hideyuki (1989), Teoría del anillo conmutativo , Estudios de Cambridge en Matemáticas Avanzadas (2ª ed.), Cambridge University Press , ISBN 978-0-521-36764-6
• Pinter-Lucke, James (2007), "Condiciones de conmutatividad para anillos: 1950-2005", Expositiones Mathematicae , 25 (2): 165-174, doi : 10.1016/j.exmath.2006.07.001 , ISSN  0723-0869

Otras lecturas

• Atiyah, Michael ; Macdonald, IG (1969), Introducción al álgebra conmutativa , Addison-Wesley Publishing Co.
• Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Anillos conmutativos noetherianos y de Krull , Serie Ellis Horwood: Matemáticas y sus aplicaciones, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
• Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimensión, multiplicidad y métodos homológicos , Serie Ellis Horwood: Matemáticas y sus aplicaciones., Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
• Kaplansky, Irving (1974), Anillos conmutativos (edición revisada), University of Chicago Press , MR  0345945
• Nagata, Masayoshi (1975) [1962], Anillos locales , Interscience Tracts in Pure and Applied Mathematics, vol. 13, Interscience Publishers, págs. xiii+234, ISBN 978-0-88275-228-0, SEÑOR  0155856
• Zariski, Óscar ; Samuel, Pierre (1958–60), Álgebra conmutativa I, II , Serie universitaria de matemáticas superiores, Princeton, Nueva Jersey: D. van Nostrand, Inc. (Reimpreso en 1975–76 por Springer como volúmenes 28–29 de Graduate Texts in Mathematics).