La proyección de Mercator ( / m ər ˈ k eɪ t ər / ) es una proyección cartográfica cilíndrica conforme presentada por el geógrafo y cartógrafo flamenco Gerardus Mercator en 1569. Se convirtió en la proyección cartográfica estándar para la navegación debido a su capacidad para representar el norte como "arriba". y el sur como "abajo" en todas partes, preservando al mismo tiempo las direcciones y formas locales. Sin embargo, como resultado, la proyección de Mercator aumenta el tamaño de los objetos cuanto más se alejan del ecuador. En una proyección de Mercator, masas de tierra como Groenlandia y la Antártida parecen mucho más grandes de lo que realmente son en relación con las masas de tierra cercanas al ecuador. A pesar de estos inconvenientes, la proyección de Mercator se adapta bien a la navegación marítima y a los mapas web de Internet y sigue utilizándose ampliamente en la actualidad. [1]
Existe cierta controversia sobre los orígenes del Mercator. El erudito alemán Erhard Etzlaub grabó "mapas de brújula" en miniatura (de unos 10 × 8 cm) de Europa y partes de África que abarcaban latitudes de 0° a 67° para permitir el ajuste de sus relojes de sol portátiles de bolsillo . John Snyder [2] afirmó en 1987 que la proyección encontrada en estos mapas, que data de 1511, era la misma proyección que la de Mercator. Sin embargo, dada la geometría de un reloj de sol, estos mapas bien pueden haberse basado en la proyección cilíndrica central similar , un caso límite de la proyección gnomónica , que es la base de un reloj de sol. Snyder modificó su evaluación a "una proyección similar" en 1993. [3]
Joseph Needham , un historiador de China, especuló que algunos mapas estelares de la dinastía Song china pueden haberse basado en la proyección de Mercator; [4] sin embargo, esta afirmación se presentó sin pruebas, y el historiador astronómico Kazuhiko Miyajima concluyó mediante análisis cartmétrico que estos mapas utilizaban una proyección equirectangular . [5]
El matemático y cosmógrafo portugués Pedro Nunes describió por primera vez el principio matemático del loxódromo y su uso en la navegación marítima . En 1537, propuso construir un atlas náutico compuesto por varias hojas de gran escala en proyección equirectangular como una forma de minimizar la distorsión de las direcciones. Si estas láminas se llevaran a la misma escala y se ensamblaran, se aproximarían a la proyección de Mercator.
En 1569, Gerhard Kremer, conocido por su nombre comercial Gerardus Mercator, anunció una nueva proyección publicando un gran mapa planisférico que medía 202 por 124 cm (80 por 49 pulgadas) e impreso en dieciocho hojas separadas. Mercator tituló el mapa Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata : "Una descripción nueva y aumentada de la Tierra corregida para el uso de marineros". Este título, junto con una explicación detallada sobre el uso de la proyección que aparece como una sección de texto en el mapa, muestra que Mercator entendió exactamente lo que había logrado y que pretendía que la proyección ayudara a la navegación. Mercator nunca explicó el método de construcción ni cómo llegó a él. A lo largo de los años se han presentado varias hipótesis, pero en cualquier caso, la amistad de Mercator con Pedro Nunes y su acceso a las tablas loxodrómicas que creó Nunes probablemente ayudaron en sus esfuerzos.
El matemático inglés Edward Wright publicó las primeras tablas precisas para construir la proyección en 1599 y, con más detalle, en 1610, titulando su tratado "Ciertos errores en la navegación". La primera formulación matemática fue publicada alrededor de 1645 por un matemático llamado Henry Bond ( c. 1600 –1678). Sin embargo, las matemáticas involucradas fueron desarrolladas pero nunca publicadas por el matemático Thomas Harriot alrededor de 1589. [6]
El desarrollo de la proyección Mercator representó un gran avance en la cartografía náutica del siglo XVI. Sin embargo, se adelantó mucho a su tiempo, ya que las antiguas técnicas de navegación y topografía no eran compatibles con su uso en la navegación. Dos problemas principales impidieron su aplicación inmediata: la imposibilidad de determinar la longitud en el mar con la precisión adecuada y el hecho de que en la navegación se utilizaban direcciones magnéticas, en lugar de direcciones geográficas . Sólo a mediados del siglo XVIII, después de que se inventó el cronómetro marino y se conoció la distribución espacial de la declinación magnética , los navegantes pudieron adoptar plenamente la proyección de Mercator.
A pesar de esas limitaciones para encontrar la posición, la proyección de Mercator se puede encontrar en muchos mapas mundiales en los siglos posteriores a la primera publicación de Mercator. Sin embargo, no empezó a dominar los mapas mundiales hasta el siglo XIX, cuando el problema de la determinación de la posición se había resuelto en gran medida. Una vez que Mercator se convirtió en la proyección habitual para mapas comerciales y educativos, fue objeto de persistentes críticas por parte de los cartógrafos por su representación desequilibrada de las masas continentales y su incapacidad para mostrar de manera útil las regiones polares.
Las críticas formuladas contra el uso inadecuado de la proyección Mercator dieron lugar a una avalancha de nuevos inventos a finales del siglo XIX y principios del XX, a menudo promocionados directamente como alternativas a Mercator. Debido a estas presiones, los editores redujeron gradualmente el uso de la proyección a lo largo del siglo XX. Sin embargo, la llegada del mapeo web le dio a la proyección un resurgimiento abrupto en la forma de la proyección Web Mercator .
Hoy en día, el Mercator se puede encontrar en cartas marinas, mapas mundiales ocasionales y servicios cartográficos web, pero los atlas comerciales lo han abandonado en gran medida, y los mapas murales del mundo se pueden encontrar en muchas proyecciones alternativas. Google Maps , que dependió de él desde 2005, todavía lo usa para mapas de áreas locales, pero eliminó la proyección de las plataformas de escritorio en 2017 para mapas que están alejados de áreas locales. Muchos otros servicios de mapas en línea todavía utilizan exclusivamente Web Mercator.
Como en todas las proyecciones cilíndricas , los paralelos y meridianos del Mercator son rectos y perpendiculares entre sí. Para lograr esto, la inevitable extensión este-oeste del mapa, que aumenta a medida que aumenta la distancia desde el ecuador , va acompañada en la proyección de Mercator por una correspondiente extensión norte-sur, de modo que en cada punto la escala este-oeste es Lo mismo que la escala norte-sur, lo que la convierte en una proyección cartográfica conforme . Las proyecciones conformes preservan los ángulos alrededor de todas las ubicaciones.
Debido a que la escala lineal de un mapa de Mercator aumenta con la latitud, distorsiona el tamaño de los objetos geográficos alejados del ecuador y transmite una percepción distorsionada de la geometría general del planeta. En latitudes superiores a 70° norte o sur, la proyección de Mercator es prácticamente inutilizable, porque la escala lineal se vuelve infinitamente grande en los polos. Por lo tanto, un mapa de Mercator nunca puede mostrar completamente las áreas polares (siempre que la proyección se base en un cilindro centrado en el eje de rotación de la Tierra; consulte la proyección transversal de Mercator para otra aplicación).
La proyección de Mercator traza trayectorias de rumbo constante (llamadas líneas de rumbo o loxódromos ) en líneas rectas y, por lo tanto, es especialmente adecuada para la navegación marítima : los rumbos y rumbos se miden utilizando una rosa de los vientos o un transportador, y las direcciones correspondientes se transfieren fácilmente de un punto a otro. punto, en el mapa, por ejemplo, con la ayuda de una regla paralela .
La proyección de Mercator a menudo se compara y se confunde con la proyección cilíndrica central , que es el resultado de proyectar puntos de la esfera sobre un cilindro tangente a lo largo de líneas radiales rectas, como si provinieran de una fuente de luz colocada en el centro de la Tierra. [7] Ambos tienen una distorsión extrema lejos del ecuador y no pueden mostrar los polos. Sin embargo, son proyecciones diferentes y tienen propiedades diferentes.
Como en todas las proyecciones cartográficas , las formas o tamaños son distorsiones de la verdadera disposición de la superficie terrestre.
La proyección de Mercator exagera las zonas alejadas del ecuador .
Debido a las grandes distorsiones de la superficie terrestre, críticos como George Kellaway e Irving Fisher consideran que la proyección no es adecuada para mapas mundiales generales. Debido a que muestra a los países cerca del ecuador como demasiado pequeños en comparación con los de Europa y América del Norte, se ha supuesto [ ¿ por quién? ] para hacer que la gente considere a esos países como menos importantes. [9] El propio Mercator utilizó la proyección sinusoidal de áreas iguales para mostrar áreas relativas. Sin embargo, a pesar de tales críticas, la proyección de Mercator fue, especialmente a finales del siglo XIX y principios del XX, quizás la proyección más común utilizada en los mapas mundiales. [10] [11] [12]
Los atlas dejaron en gran medida de utilizar la proyección de Mercator para mapas mundiales o para áreas distantes del ecuador en la década de 1940, prefiriendo otras proyecciones cilíndricas o formas de proyección de áreas iguales . Sin embargo, la proyección de Mercator todavía se utiliza comúnmente en áreas cercanas al ecuador donde la distorsión es mínima. También se encuentra frecuentemente en mapas de zonas horarias. [13] Debido a su uso común, la proyección de Mercator ha sido supuesta [ ¿por quién? ] haber influido en la visión que la gente tenía del mundo. [14]
Arno Peters generó controversia a partir de 1972 cuando propuso lo que ahora se suele llamar proyección Gall-Peters para remediar los problemas del Mercator, afirmando que era su propio trabajo original sin hacer referencia a trabajos anteriores de cartógrafos como el trabajo de Gall de 1855. La proyección que promovió es una parametrización específica de la proyección cilíndrica de áreas iguales . En respuesta, una resolución de 1989 de siete grupos geográficos norteamericanos menospreció el uso de proyecciones cilíndricas para mapas mundiales de uso general, que incluirían tanto al Mercator como al Gall-Peters. [15]
Prácticamente todas las cartas náuticas impresas se basan en la proyección de Mercator debido a sus propiedades excepcionalmente favorables para la navegación. También lo utilizan habitualmente los servicios de mapas de calles alojados en Internet, debido a sus propiedades excepcionalmente favorables para los mapas de áreas locales calculados bajo demanda. [16] Las proyecciones de Mercator también fueron importantes en el desarrollo matemático de la tectónica de placas en la década de 1960. [17]
La proyección Mercator fue diseñada para su uso en la navegación marítima debido a su propiedad única de representar cualquier curso de rumbo constante como un segmento recto. Este rumbo, conocido como rumbo (alternativamente llamado línea de rumbo o loxódromo) se prefiere en la navegación marítima porque los barcos pueden navegar en una dirección constante de la brújula. Esto reduce las correcciones de rumbo difíciles y propensas a errores que de otro modo serían necesarias al navegar un rumbo diferente.
Para distancias pequeñas (en comparación con el radio de la Tierra), la diferencia entre el rumbo y el rumbo del círculo máximo es insignificante. Incluso para distancias más largas, la simplicidad del rumbo constante lo hace atractivo. Como observa Mercator, con tal rumbo el barco no llegaría por la ruta más corta, pero seguramente llegará. Navegar en rumbo significaba que todo lo que los marineros tenían que hacer era mantener un rumbo constante siempre y cuando supieran dónde estaban cuando comenzaron, dónde pretendían estar cuando terminaran y tuvieran un mapa en proyección Mercator que mostrara correctamente esos dos. coordenadas. [18]
Muchos de los principales servicios de mapas de calles en línea ( Bing Maps , Google Maps , Mapbox , MapQuest , OpenStreetMap , Yahoo! Maps y otros) utilizan una variante de la proyección de Mercator para sus imágenes de mapas [19] llamada Web Mercator o Google Web Mercator. A pesar de su obvia variación de escala a nivel mundial (pequeñas escalas), la proyección es muy adecuada como mapa mundial interactivo que se puede ampliar sin problemas a mapas locales (a gran escala), donde hay relativamente poca distorsión debido a la variante de proyección. casi conformidad .
Los sistemas de mosaico de los principales servicios de mapas de calles en línea muestran la mayor parte del mundo en el nivel de zoom más bajo como una única imagen cuadrada, excluyendo las regiones polares mediante truncamiento en latitudes de φ max = ±85,05113°. (Ver más abajo.) Los valores de latitud fuera de este rango se mapean utilizando una relación diferente que no diverge en φ = ±90°. [ cita necesaria ]
Aunque la superficie de la Tierra se modela mejor mediante un elipsoide achatado de revolución , para mapas a pequeña escala el elipsoide se aproxima mediante una esfera de radio a , donde a es aproximadamente 6.371 km. Esta aproximación esférica de la Tierra se puede modelar mediante una esfera más pequeña de radio R , llamada globo en esta sección. El globo terráqueo determina la escala del mapa. Las distintas proyecciones cilíndricas especifican cómo se transfiere el detalle geográfico del globo a un cilindro tangencial a él en el ecuador. Luego se desenrolla el cilindro para obtener el mapa plano. [20] [21] [ página necesaria ] La fracciónR/ase llama fracción representativa (RF) o escala principal de la proyección. Por ejemplo, un mapa de Mercator impreso en un libro podría tener un ancho ecuatorial de 13,4 cm correspondiente a un radio de globo de 2,13 cm y un RF de aproximadamente1/300M(M se utiliza como abreviatura de 1.000.000 al escribir un RF), mientras que el mapa original de Mercator de 1569 tiene un ancho de 198 cm correspondiente a un radio de globo de 31,5 cm y un RF de aproximadamente1/20M.
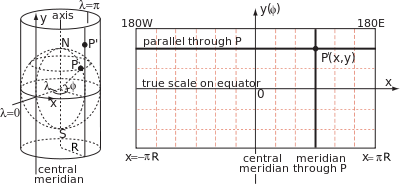
Una proyección de mapa cilíndrica se especifica mediante fórmulas que vinculan las coordenadas geográficas de latitud φ y longitud λ con las coordenadas cartesianas en el mapa con origen en el ecuador y eje x a lo largo del ecuador. Por construcción, todos los puntos en el mismo meridiano se encuentran en el mismo generador [a] del cilindro a un valor constante de x , pero la distancia y a lo largo del generador (medida desde el ecuador) es una función arbitraria [b] de la latitud, y ( φ ). En general, esta función no describe la proyección geométrica (como la de los rayos de luz sobre una pantalla) desde el centro del globo hasta el cilindro, que es sólo una entre un número ilimitado de formas de proyectar conceptualmente un mapa cilíndrico.
Dado que el cilindro es tangencial al globo en el ecuador, el factor de escala entre el globo y el cilindro es la unidad en el ecuador, pero en ningún otro lugar. En particular, dado que el radio de un paralelo, o círculo de latitud, es R cos φ , el paralelo correspondiente en el mapa debe haberse alargado por un factor de1/porque φ= segundo φ . Este factor de escala en el paralelo se denota convencionalmente por k y el factor de escala correspondiente en el meridiano se denota por h . [22]
La proyección de Mercator es conforme . Una implicación de esto es la "isotropía de los factores de escala", lo que significa que el factor de escala puntual es independiente de la dirección, de modo que la proyección preserva las formas pequeñas. Esto implica que el factor de escala vertical, h , es igual al factor de escala horizontal, k . Dado que k = sec φ , también debe hacerlo h .
El gráfico muestra la variación de este factor de escala con la latitud. Algunos valores numéricos se enumeran a continuación.
El factor de escala de área es el producto de las escalas paralela y meridiana hk = sec 2 φ . Para Groenlandia, tomando 73° como latitud media, hk = 11,7. Para Australia, tomando 25° como latitud media, hk = 1,2. Para Gran Bretaña, tomando 55° como latitud media, hk = 3,04.
La variación con la latitud a veces se indica mediante múltiples escalas de barras , como se muestra a continuación.
La forma clásica de mostrar la distorsión inherente a una proyección es utilizar la indicatriz de Tissot . Nicolas Tissot señaló que los factores de escala en un punto de una proyección cartográfica, especificado por los números h y k , definen una elipse en ese punto. Para proyecciones cilíndricas, los ejes de la elipse están alineados con los meridianos y paralelos. [23] [c] Para la proyección de Mercator, h = k , por lo que las elipses degeneran en círculos con radio proporcional al valor del factor de escala para esa latitud. Estos círculos se representan en el mapa proyectado con una variación extrema de tamaño, indicativa de las variaciones de escala de Mercator.
Como se analizó anteriormente, la condición de isotropía implica que h = k = sec φ . Considere un punto en el globo de radio R con longitud λ y latitud φ . Si φ se incrementa en una cantidad infinitesimal, dφ , el punto se mueve R dφ a lo largo de un meridiano del globo de radio R , por lo que el cambio correspondiente en y , dy , debe ser hR dφ = R sec φ dφ . Por lo tanto y′ ( φ ) = R sec φ . De manera similar, aumentar λ en dλ mueve el punto R cos φ dλ a lo largo de un paralelo del globo, por lo que dx = kR cos φ dλ = R dλ . Es decir, x′ ( λ ) = R . Integrando las ecuaciones
con x ( λ 0 ) = 0 e y (0) = 0, da x(λ) e y(φ) . El valor λ 0 es la longitud de un meridiano central arbitrario que suele ser, aunque no siempre, el de Greenwich (es decir, cero). Los ángulos λ y φ se expresan en radianes. Por la integral de la función secante , [24] [25]
La función y ( φ ) se traza junto a φ para el caso R = 1: tiende al infinito en los polos. Los valores lineales del eje y no suelen mostrarse en los mapas impresos; en cambio, algunos mapas muestran la escala no lineal de valores de latitud a la derecha. La mayoría de las veces los mapas muestran sólo una retícula de meridianos y paralelos seleccionados.
La expresión a la derecha de la segunda ecuación define la función gudermanniana ; es decir, φ = gd(y/R): la ecuación directa puede por tanto escribirse como y = R ·gd −1 ( φ ). [24]
Hay muchas expresiones alternativas para y ( φ ), todas derivadas de manipulaciones elementales. [25]
Las inversas correspondientes son:
Para ángulos expresados en grados:
Las fórmulas anteriores están escritas en términos del radio del globo R. A menudo es conveniente trabajar directamente con el ancho del mapa W = 2 π R . Por ejemplo, las ecuaciones de transformación básicas se convierten en
La ordenada y de la proyección de Mercator se vuelve infinita en los polos y el mapa debe truncarse en alguna latitud inferior a noventa grados. No es necesario hacerlo simétricamente. El mapa original de Mercator está truncado en 80°N y 66°S con el resultado de que los países europeos fueron movidos hacia el centro del mapa. La relación de aspecto de su mapa es198/120= 1,65. Se han utilizado truncamientos aún más extremos: un atlas escolar finlandés fue truncado aproximadamente a 76°N y 56°S, una relación de aspecto de 1,97.
Gran parte de los mapas basados en la Web utilizan una versión ampliable de la proyección de Mercator con una relación de aspecto de uno. En este caso la latitud máxima alcanzada debe corresponder a y = ±W./2, o equivalentey/R = π . Para calcular las latitudes correspondientes se puede utilizar cualquiera de las fórmulas de transformación inversa:
Las relaciones entre y ( φ ) y las propiedades de la proyección, como la transformación de ángulos y la variación de escala, se derivan de la geometría de los elementos pequeños correspondientes en el globo y el mapa. La siguiente figura muestra un punto P en latitud φ y longitud λ en el globo y un punto cercano Q en latitud φ + δφ y longitud λ + δλ . Las líneas verticales PK y MQ son arcos de meridianos de longitud Rδφ . [d] Las rectas horizontales PM y KQ son arcos de paralelas de longitud R (cos φ ) δλ . Los puntos correspondientes en la proyección definen un rectángulo de ancho δx y alto δy .
Para elementos pequeños, el ángulo PKQ es aproximadamente un ángulo recto y por lo tanto
Los factores de escala mencionados anteriormente del globo al cilindro están dados por
Dado que los meridianos están asignados a líneas de x constante , debemos tener x = R ( λ − λ 0 ) y δx = Rδλ , ( λ en radianes). Por tanto, en el límite de elementos infinitamente pequeños
En el caso de la proyección de Mercator, y' ( φ ) = R sec φ , esto nos da h = k y α = β . El hecho de que h = k es la isotropía de los factores de escala discutidos anteriormente. El hecho de que α = β refleja otra implicación de que el mapeo sea conforme, es decir, el hecho de que un rumbo de navegación de azimut constante en el globo se mapea en la misma cuadrícula constante que marca el mapa.
Convertir la distancia de la regla en el mapa de Mercator en distancia verdadera ( círculo máximo ) en la esfera es sencillo a lo largo del ecuador, pero en ningún otro lugar. Un problema es la variación de la escala con la latitud, y otro es que las líneas rectas en el mapa ( líneas de rumbo ), distintas de los meridianos o el ecuador, no corresponden a círculos máximos.
Mercator entendió claramente la distinción entre distancia de rumbo (navegación) y distancia de círculo máximo (verdadera). (Ver Leyenda 12 en el mapa de 1569.) Hizo hincapié en que la distancia de la línea de rumbo es una aproximación aceptable para la distancia verdadera del gran círculo para cursos de distancia corta o moderada, particularmente en latitudes más bajas. Incluso cuantifica su afirmación: "Cuando las distancias del círculo máximo que se miden en las proximidades del ecuador no exceden los 20 grados de un círculo máximo, o los 15 grados cerca de España y Francia, o los 8 e incluso 10 grados en las partes del norte es conveniente utilizar distancias de líneas de rumbo".
Para una medición con regla de una línea corta , con punto medio en la latitud φ , donde el factor de escala es k = sec φ = 1/porque φ:
Con un radio y una circunferencia máxima iguales a 6.371 km y 40.030 km respectivamente, un RF de1/300M, para el cual R = 2,12 cm y W = 13,34 cm, implica que una medida de regla es de 3 mm. en cualquier dirección desde un punto del ecuador corresponde aproximadamente a 900 km. Las distancias correspondientes para las latitudes 20°, 40°, 60° y 80° son 846 km, 689 km, 450 km y 156 km respectivamente.
Las distancias más largas requieren varios enfoques.
La escala es la unidad en el ecuador (para una proyección no secante). Por lo tanto, interpretar las medidas de la regla en el ecuador es sencillo:
Para el modelo anterior, con RF = 1/300M, 1 cm corresponde a 3.000 km.
En cualquier otro paralelo, el factor de escala es sec φ , de modo que
Para el modelo anterior, 1 cm corresponde a 1.500 km a una latitud de 60°.
Esta no es la distancia más corta entre los puntos finales elegidos en el paralelo porque un paralelo no es un círculo máximo. La diferencia es pequeña para distancias cortas pero aumenta a medida que aumenta λ , la separación longitudinal. Para dos puntos, A y B, separados por 10° de longitud en el paralelo a 60°, la distancia a lo largo del paralelo es aproximadamente 0,5 km mayor que la distancia del gran círculo. (La distancia AB a lo largo del paralelo es ( a cos φ ) λ . La longitud de la cuerda AB es 2( a cos φ ) sen λ/2. Esta cuerda subtiende un ángulo en el centro igual a 2arcsen(cos φ sen λ/2) y la distancia del círculo máximo entre A y B es 2 a arcosen(cos φ sen λ/2).) En el caso extremo en que la separación longitudinal sea de 180°, la distancia a lo largo del paralelo será la mitad de la circunferencia de ese paralelo; es decir, 10.007,5 km. Por otra parte, la geodésica entre estos puntos es un arco de círculo máximo que pasa por el polo y forma un ángulo de 60° en el centro: la longitud de este arco es una sexta parte de la circunferencia del círculo máximo, unos 6.672 km. La diferencia es de 3.338 km, por lo que la distancia de la regla medida en el mapa es bastante engañosa incluso después de corregir la variación de latitud del factor de escala.
Un meridiano del mapa es un gran círculo en el globo, pero la variación continua de la escala significa que la medición con regla por sí sola no puede determinar la distancia real entre puntos distantes en el meridiano. Sin embargo, si el mapa está marcado con una escala de latitud precisa y finamente espaciada desde la cual se puede leer directamente la latitud, como es el caso del mapa mundial Mercator 1569 (hojas 3, 9, 15) y todas las cartas náuticas posteriores, el meridiano La distancia entre dos latitudes φ 1 y φ 2 es simplemente
Si las latitudes de los puntos finales no se pueden determinar con confianza, se pueden encontrar calculando la distancia de la regla. Llamando a las distancias de la regla de los puntos finales en el meridiano del mapa medido desde el ecuador y 1 e y 2 , la distancia verdadera entre estos puntos en la esfera se obtiene usando cualquiera de las fórmulas inversas de Mercator:
donde R puede calcularse a partir del ancho W del mapa mediante R = W./2 π. Por ejemplo, en un mapa con R = 1 los valores de y = 0, 1, 2, 3 corresponden a latitudes de φ = 0°, 50°, 75°, 84° y por tanto los intervalos sucesivos de 1 cm en el mapa corresponden a intervalos de latitud en el globo de 50°, 25°, 9° y distancias de 5.560 km, 2.780 km y 1.000 km en la Tierra.
Una línea recta en el mapa de Mercator que forma un ángulo α con los meridianos es una línea de rumbo . Cuando α = π/2o3 π/2el rumbo corresponde a uno de los paralelos; sólo uno, el ecuador, es un círculo máximo. Cuando α = 0 o π corresponde a un meridiano de círculo máximo (si continúa alrededor de la Tierra). Para todos los demás valores, es una espiral de polo a polo en el globo que cruza todos los meridianos en el mismo ángulo y, por lo tanto, no es un círculo máximo. [25] Esta sección analiza sólo el último de estos casos.
Si α no es ni 0 ni π , entonces la figura anterior de los elementos infinitesimales muestra que la longitud de una línea de rumbo infinitesimal en la esfera entre latitudes φ ; y φ + δφ es un segundo α δφ . Dado que α es constante en el rumbo, esta expresión se puede integrar para dar, para líneas de rumbo finitas en la Tierra:
Una vez más, si Δ φ puede leerse directamente desde una escala de latitud precisa en el mapa, entonces la distancia de rumbo entre puntos del mapa con latitudes φ 1 y φ 2 viene dada por lo anterior. Si no existe tal escala, entonces las distancias de la regla entre los puntos finales y el ecuador, y 1 e y 2 , dan el resultado mediante una fórmula inversa:
Estas fórmulas dan distancias de rumbo en la esfera que pueden diferir mucho de las distancias reales cuya determinación requiere cálculos más sofisticados. [mi]
Cuando la Tierra es modelada por un esferoide ( elipsoide de revolución), la proyección de Mercator debe modificarse para que siga siendo conforme . Las ecuaciones de transformación y el factor de escala para la versión no secante son [26]
El factor de escala es la unidad en el ecuador, como debe ser ya que el cilindro es tangencial al elipsoide en el ecuador. La corrección elipsoidal del factor de escala aumenta con la latitud pero nunca es mayor que e 2 , una corrección inferior al 1%. (El valor de e 2 es aproximadamente 0,006 para todos los elipsoides de referencia). Esto es mucho menor que la inexactitud de la escala, excepto muy cerca del ecuador. Sólo las proyecciones precisas de Mercator de regiones cercanas al ecuador necesitarán correcciones elipsoidales.
Lo inverso se resuelve de forma iterativa, ya que está involucrada la latitud isométrica .
![{\displaystyle x=R(\lambda -\lambda _{0}),\qquad y=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\ varphi }{2}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62ea14e55f1e378a2a82a2ff70bee9d2f8cabf8d)
![{\displaystyle \lambda =\lambda _{0}+{\frac {x}{R}},\qquad \varphi =2\tan ^{-1}\left[\exp \left({\frac {y }{R}}\right)\right]-{\frac {\pi }{2}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc1b673f6fcbd95688246bf8c30af7fdd9214ec)
![{\displaystyle {\begin{aligned}y&=&{\frac {R}{2}}\ln \left[{\frac {1+\sin \varphi }{1-\sin \varphi }}\right] &=&{R}\ln \left[{\frac {1+\sin \varphi }{\cos \varphi }}\right]&=R\ln \left(\sec \varphi +\tan \varphi \ derecha)\\[2ex]&=&R\tanh ^{-1}\left(\sin \varphi \right)&=&R\sinh ^{-1}\left(\tan \varphi \right)&=R \operatorname {sgn} (\varphi )\cosh ^{-1}\left(\sec \varphi \right)=R\operatorname {gd} ^{-1}(\varphi ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae347eb9bffadb5f8004faa0d0c1e212839b58a1)
![{\displaystyle x={\frac {\pi R(\lambda ^{\circ }-\lambda _{0}^{\circ })}{180}},\qquad \quad y=R\ln \left [\tan \left(45+{\frac {\varphi ^{\circ }}{2}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcc9392cd18cd854770761b77b8d37a0633c1354)
![{\displaystyle x={\frac {W}{2\pi }}\left(\lambda -\lambda _{0}\right),\qquad \quad y={\frac {W}{2\pi } }\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7abeaed8bf4f766e4eb931035dfbbf787caa6c0)
![{\displaystyle \varphi =\tan ^{-1}\left[\sinh \left({\frac {y}{R}}\right)\right]=\tan ^{-1}\left[\sinh \pi \right]=\tan ^{-1}\left[11.5487\right]=85.05113^{\circ }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e455a07f94771d84de1d2c0de4e0ed371c3858c)
![{\displaystyle m_{12}=a\left|\tan ^{-1}\left[\sinh \left({\frac {y_{1}}{R}}\right)\right]-\tan ^ {-1}\left[\sinh \left({\frac {y_ {2}}{R}}\right)\right]\right|,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47121a7581ab0e8d755c23df8ac6708bfe8d57c4)
![{\displaystyle {\begin{aligned}x&=R\left(\lambda -\lambda _{0}\right),\\y&=R\ln \left[\tan \left({\frac {\pi } {4}}+{\frac {\varphi }{2}}\right)\left({\frac {1-e\sin \varphi }{1+e\sin \varphi }}\right)^{\ frac {e}{2}}\right]=R\left(\sinh ^{-1}\left(\tan \varphi \right)-e\tanh ^{-1}(e\sin \varphi )\ derecha),\\k&=\sec \varphi {\sqrt {1-e^{2}\sin ^{2}\varphi }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/378a7fde0b2ede2f7f7b1b663f9e00c5aa34cea9)
