Teoría de Debye-Hückel
La no idealidad de soluciones más concentradas surge principalmente (pero no exclusivamente) porque los iones de carga opuesta se atraen entre sí debido a las fuerzas electrostáticas , mientras que los iones de la misma carga se repelen entre sí.
Fue encontrado para dar excelente acuerdo para soluciones "diluidas".
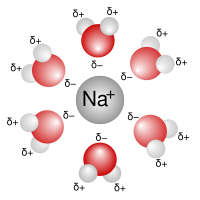
Los iones se muestran como esferas con carga eléctrica unitaria.
El disolvente (azul pálido) se muestra como un medio uniforme, sin estructura.
Estos conceptos se desarrollaron en una teoría cuantitativa que involucraba iones de carga z1e+ y z2e-, donde z puede ser cualquier número entero.
El supuesto principal es que la desviación de la idealidad se debe a las interacciones electrostáticas entre iones, mediadas por la ley de Coulomb: la fuerza de interacción entre dos cargas eléctricas, separadas por una distancia, r en un medio de permitividad relativa ε r viene dada por[6] También se asume que El último supuesto significa que cada catión está rodeado por una nube esféricamente simétrica de otros iones.
De manera similar, cada anión está rodeado por una nube con carga neta positiva.
Para calcular esta energía se necesitan dos pasos.
El primer paso es especificar el potencial electrostático para el ion j por medio de la ecuación de Poisson ψ ( r ) es el potencial total a una distancia, r , desde el ion central y ρ ( r ) es la densidad de carga promediada de la nube circundante a esa distancia.
Para aplicar esta fórmula es esencial que la nube tenga simetría esférica, es decir, la densidad de carga es una función solo de la distancia desde el ion central, ya que esto permite que la ecuación de Poisson se emita en términos de coordenadas esféricas sin dependencia angular.
[7] donde k B es la constante de Boltzmann y T es la temperatura.
Esta distribución también depende del potencial ψ (r) y esto introduce una seria dificultad en términos del principio de superposición .
Debye y Hückel expandieron la exponencial como una serie de Taylor truncada a primer orden.
Para electrolitos simétricos, esto se reduce a la ecuación esférica modificada de Bessel Los coeficientes
, que es la distancia del acercamiento más cercano de los iones, la fuerza ejercida por la carga debe ser equilibrada por la fuerza de otros iones, imponiendo
es Esta es la energía potencial de un solo ion en una solución.
Para valores muy bajos de la fuerza iónica, el valor del denominador en la expresión anterior se vuelve casi igual a uno.
Esto se conoce como la ley limitante de Debye-Hückel .
proporciona un acuerdo satisfactorio con las mediciones experimentales para bajas concentraciones de electrolitos, típicamente menos de 10 −3 mol / L. Las desviaciones de la teoría ocurren en concentraciones más altas y con electrolitos que producen iones de cargas más altas, particularmente electrolitos asimétricos.
Esencialmente, estas desviaciones ocurren porque el modelo se simplifica demasiado, por lo que hay poco que ganar haciendo pequeños ajustes al modelo.
Por lo general, permiten que se siga la ecuación de Debye-Hückel a baja concentración y agregan términos adicionales en algún poder de la fuerza iónica para ajustarse a las observaciones experimentales.
La teoría puede aplicarse también a soluciones diluidas de electrolitos mixtos.
[15] El tratamiento dado hasta ahora es para un sistema que no está sujeto a un campo eléctrico externo.
Además, se asumió que el campo eléctrico hace que la nube de carga se distorsione lejos de la simetría esférica.
[16] Después de tener esto en cuenta, junto con los requisitos específicos de los iones móviles, como la viscosidad y los efectos electroforéticos, Onsager pudo derivar una expresión teórica para explicar la relación empírica conocida como la Ley de Kohlrausch, para la conductividad molar, Λm.
es conocida como la conductividad molar limitante, K es una constante empírica y c es la concentración de electrolito.
Esto se conoce como la ecuación de Debye-Hückel-Onsager.