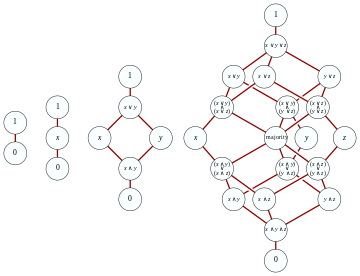
Retículo distributivo

) es distributivo si lo siguiente se cumple para todo x, y, z en L: Viendo los retículos como conjuntos parcialmente ordenados, se dice que el operador meet "preserva" un número finito y no vacío de operadores join.

Un resultado básico de la teoría de retículos es que la condición de arriba es equivalente a su dual: Otra definición equivalente es decir que L es distributivo si y sólo si lo siguiente se cumple para cualesquiera elementos x, y, z en L: Lo que a su vez es equivalente a decir Un morfismo de retículos distributivos es una función que es compatible con los dos operadores meet y join.

Los retículos distributivos son estructuras ubicuas y al mismo tiempo muy específicas.

Un retículo es distributivo si y sólo si ninguno de sus subretículos es isomorfo a M3 o N5; un subretículo es un subconjunto cerrado bajo los operadores meet y join del retículo original.

Un elemento de un retículo distributivo es meet-primo o ínfimo-primo si y sólo si es meet-irreducible o ínfimo-irreducible, aunque esta última se considera en general una propiedad más débil.

L es isomorfo a un retículo de conjuntos (cerrado bajo la unión y la intersección).

Generalizar estos resultados a retículos infinitos, sin embargo, requiere del uso de estructuras adicionales.

El retículo original es recuperado como la colección de conjuntos clopen inferiores en este espacio.

Una primera observación es que, usando las propiedades de distributividad, cada término formado por los operadores binarios

Esto ocurre cuando existen índices j y k tales que Nj es un subconjunto de Nk.

En este caso el meet de Nk estará debajo del meet de Nj, y por lo tanto se puede retirar con seguridad el conjunto redundante Nk sin cambiar la representación del término total.

En consecuencia, un conjunto de subconjuntos finitos de G se llamará irredundante siempre que todos sus elementos Ni sean mutuamente incomparables (con respecto al ordenamiento del subconjunto); lo que se cumple cuando este forma una anticadena de conjuntos finitos.