Momento magnético
La fuente de campo magnético puede ser un imán natural,un bucle de corriente eléctrica, un imán de barra, un electrón, una molécula, un planeta, etc. Tanto el momento magnético como el campo magnético pueden ser considerados como vectores con una magnitud y dirección.
El momento magnético puede definirse como un vector que relaciona el par de alineación sobre el objeto de un campo magnético aplicado externamente con el propio vector campo.
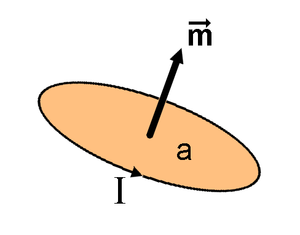
Para un bucle de corriente, esta definición conduce a que la magnitud del momento dipolar magnético es igual al producto de la corriente por el área del bucle.
Además, esta definición permite calcular el momento magnético esperado para cualquier distribución macroscópica de corriente conocida.
Una definición alternativa es útil para los cálculos termodinámicos del momento magnético.
Esta unidad tiene equivalentes en otras unidades derivadas del SI, incluyendo:[3][4]
Entre ellas, hay dos unidades alternativas (no equivalentes) de momento dipolar magnético:
donde statA es estamperios, cm es centímetros, erg es ergios, y G es gauss.
Por ejemplo, en unidades SI, una espira de corriente con corriente I y área A tiene momento magnético IA (véase más abajo), pero en unidades gaussianas el momento magnético es IA/c.
A veces, sin embargo, es útil o necesario saber cuánto del momento magnético neto del objeto es producido por una porción particular de ese imán.
Por lo tanto, es útil definir el campo de magnetización M como:
Esta ecuación se representa a menudo utilizando notación derivada tal que
donde dm es el momento magnético elemental y dV es el elemento de volumen.
Para la magnetización uniforme (donde tanto la magnitud y la dirección de M es el mismo para todo el imán (como un imán de barra recta) la última ecuación se simplifica a:
En su lugar, el parámetro que aparece es la densidad de flujo residual (o remanencia), denotada Br.
La fórmula necesaria en este caso para calcular m en (unidades de A⋅m2) es:
El alineamiento del momento dipolar magnético con el campo crea una diferencia en la energía potencial electrostática U:
En el Sistema Internacional de Unidades, el momento magnético se mide en julios sobre tesla (J/T).
Los electrones y muchos núcleos atómicos también tienen momentos magnéticos intrínsecos, cuya explicación requiera tratamiento mecanocuántico y que se relaciona con el momento angular de las partículas.
Este momento está relacionado con el hecho de que las partículas elementales tienen momento angular intrínseco o espín, para partículas cargadas eso lleva inevitablemente a que se comporten de modo similar a un pequeño circuito con cargas en movimiento.
siendo: Ciertas disposiciones orbitales, con degeneración triple o superior, implican un momento magnético adicional, por el movimiento de los electrones (partículas cargadas).
La situación es análoga a la de la espira conductora presentada arriba, pero exige un tratamiento cuántico.
La explicación clásica preferida de un momento magnético ha cambiado con el tiempo.
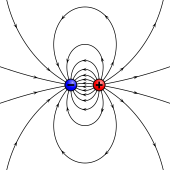
Las fuentes de momentos magnéticos en los materiales se pueden representar por polos en analogía con electrostática.
Esto a veces se conoce como el modelo de Gilbert.
Cada polo es la fuente de fuerza magnética que se debilita con la distancia.
Esta cancelación es mayor cuando los polos están cerca uno del otro, es decir, cuando la barra magnética es corta.
El momento dipolar magnético m está relacionado con los polos ficticios como[8]
La analogía con los dipolos eléctricos no debe llevarse demasiado lejos porque los dipolos magnéticos están asociados con el momento angular (ver relación con el momento angular).
Sin embargo, los polos magnéticos son muy útiles para los cálculos de magnetostática, particularmente en aplicaciones a ferromagnetos.